Time-Series of Distributions Forecasting in Agricultural Applications: An Intervals’ Numbers Approach †
Abstract
:1. Introduction
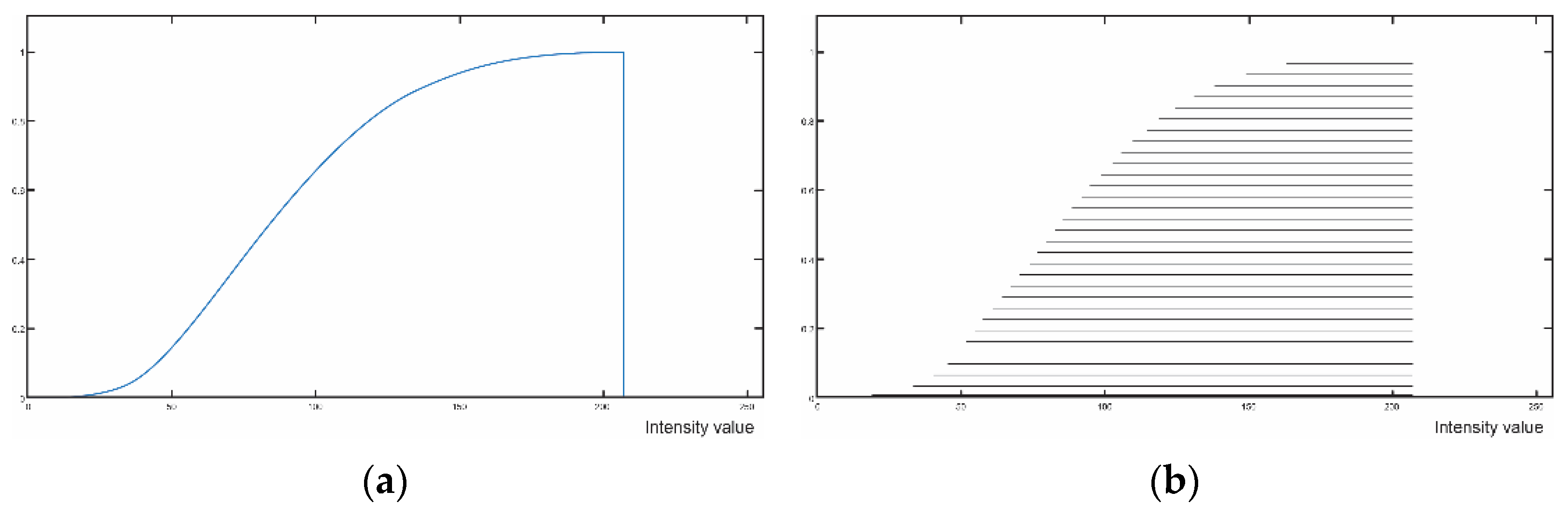
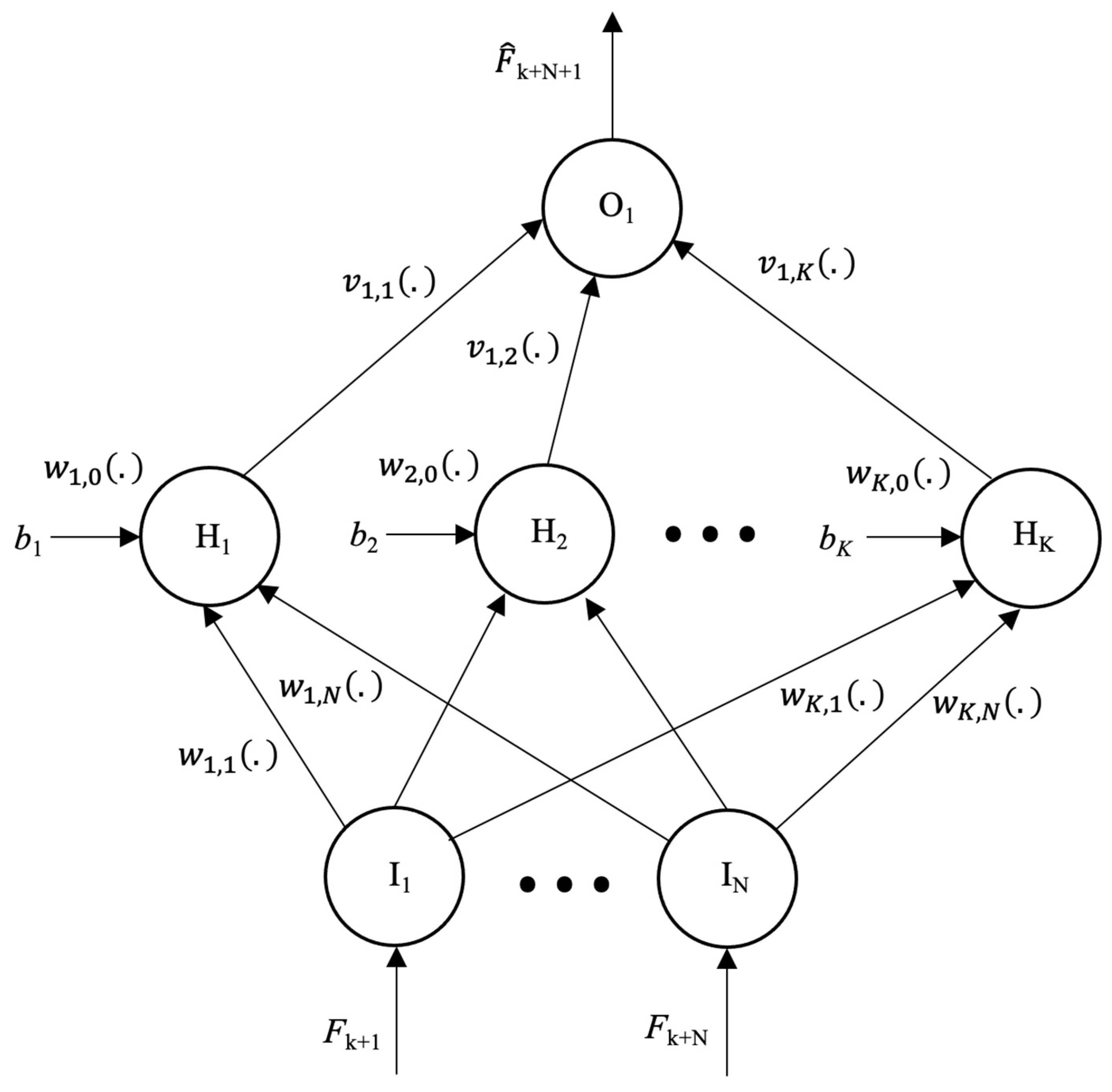
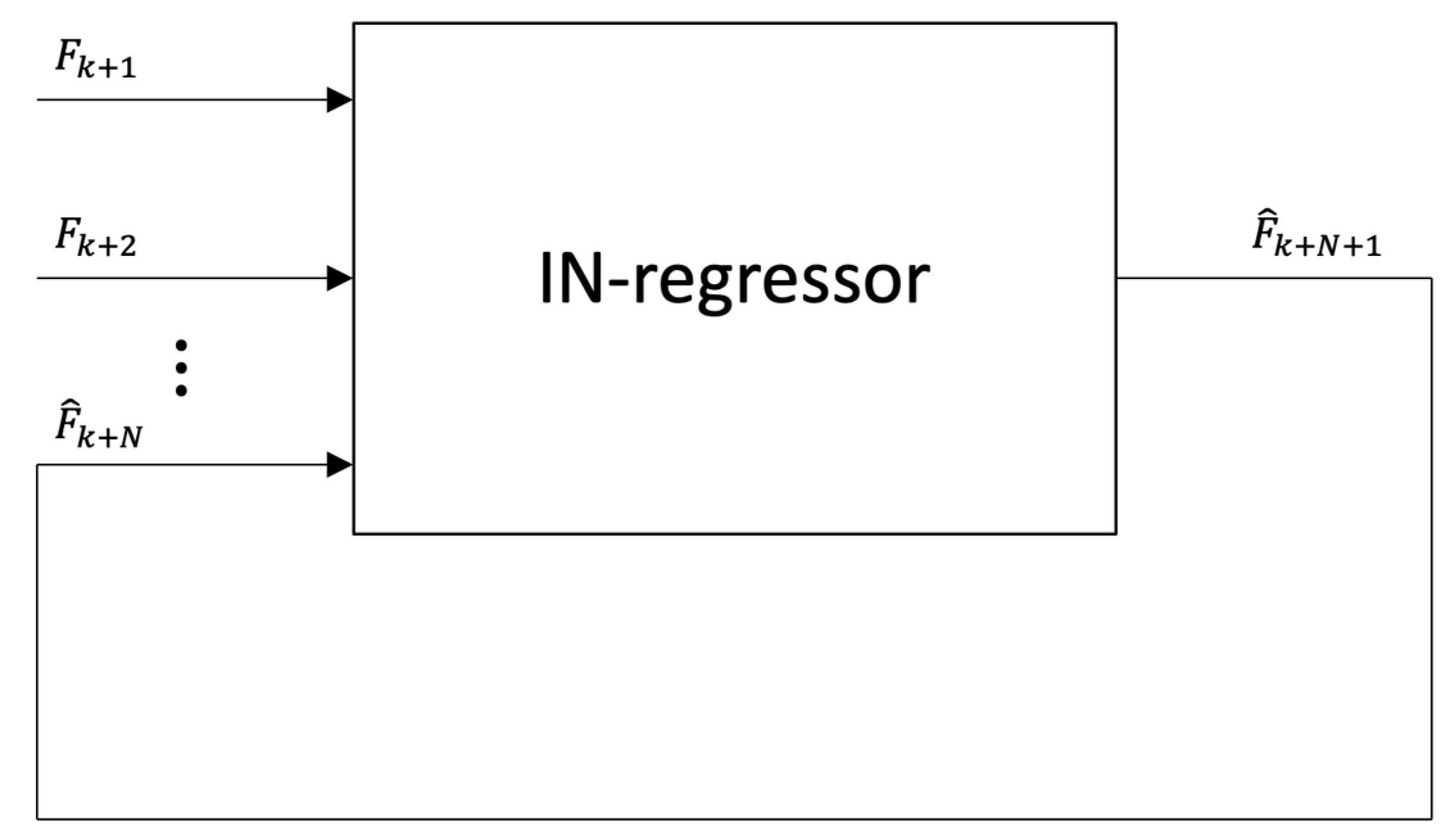
2. An IN-Regressor Parametric Models for Prediction
| Algorithm 1. IN-Regressor Training by a Genetic Algorithm (GA) |
|
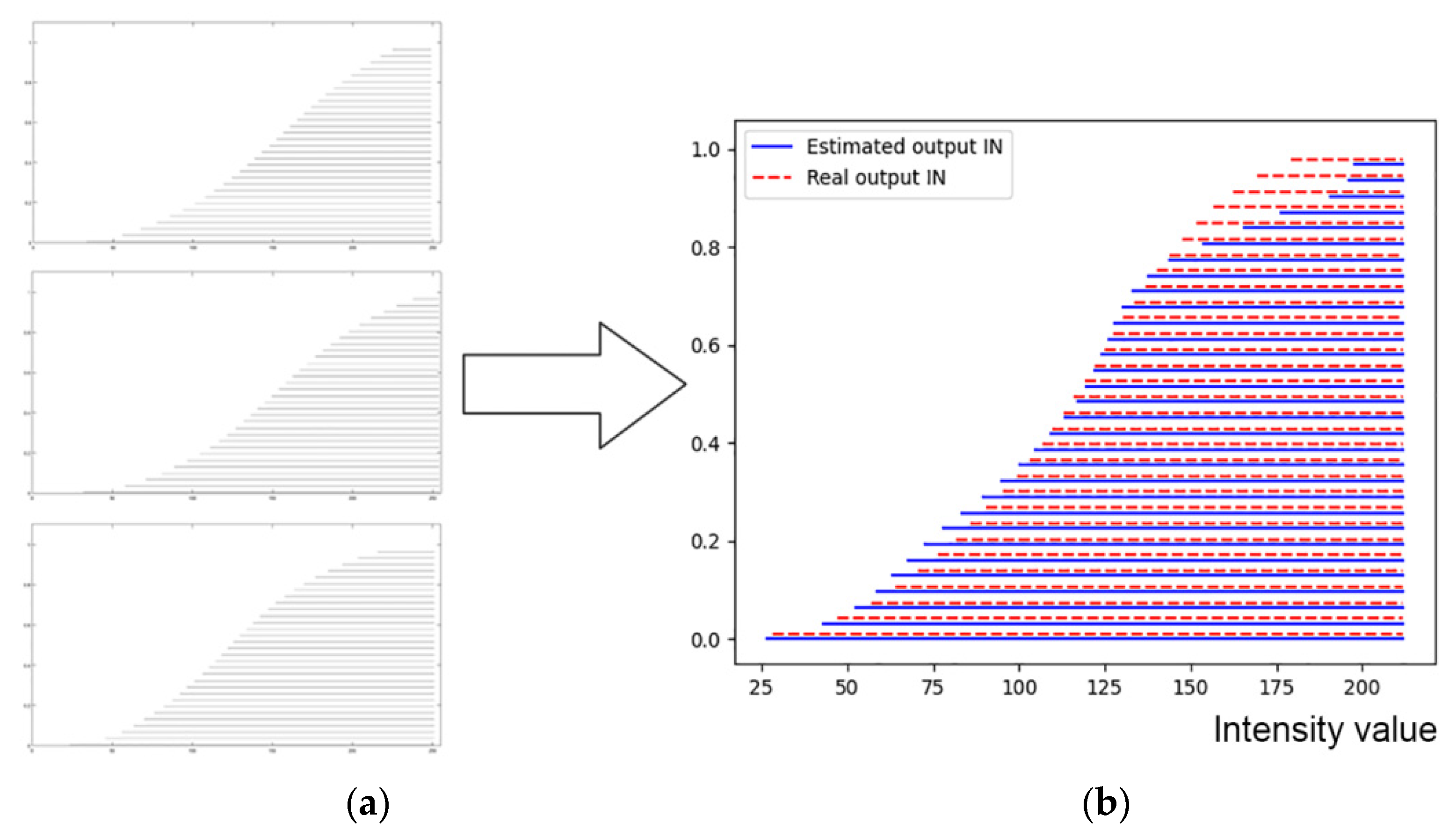
3. Experimental Results
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rose, D.C.; Wheeler, R.; Winter, M.; Lobley, M.; Chivers, C.-A. Agriculture 4.0: Making it work for people, production, and the planet. Land Use Policy 2021, 100, 104933. [Google Scholar] [CrossRef]
- Sohaib Ali Shah, S.; Zeb, A.; Qureshi, W.S.; Arslan, M.; Ullah Malik, A.; Alasmary, W.; Alanazi, E. Towards fruit maturity estimation using NIR spectroscopy. Infrared Phys. Technol. 2020, 111, 103479. [Google Scholar] [CrossRef]
- Perry, T.S. Want a Really Hard Machine Learning Problem? Try Agriculture, Says John Deere Labs. Available online: https://spectrum.ieee.org/view-from-the-valley/robotics/artificial-intelligence/want-a-really-hard-machine-learning-problem-try-agriculture-say-john-deere-labs-leaders (accessed on 19 May 2021).
- Vrochidou, E.; Tziridis, K.; Nikolaou, A.; Kalampokas, T.; Papakostas, G.A.; Pachidis, T.P.; Mamalis, S.; Koundouras, S.; Kaburlasos, V.G. An Autonomous Grape-Harvester Robot: Integrated System Architecture. Electronics 2021, 10, 1056. [Google Scholar] [CrossRef]
- Mehdizadeh, S. Using AR, MA, and ARMA Time Series Models to Improve the Performance of MARS and KNN Approaches in Monthly Precipitation Modeling under Limited Climatic Data. Water Resour. Manag. 2020, 34, 263–282. [Google Scholar] [CrossRef]
- Wang, Q.; Li, S.; Li, R.; Ma, M. Forecasting U.S. shale gas monthly production using a hybrid ARIMA and metabolic nonlinear grey model. Energy 2018, 160, 378–387. [Google Scholar] [CrossRef]
- Tealab, A.; Hefny, H.; Badr, A. Forecasting of nonlinear time series using ANN. Futur. Comput. Inform. J. 2017, 2, 39–47. [Google Scholar] [CrossRef]
- Raj, J.S.; Ananthi, J.V. Reccurent Neural Networks and Nonlinear Prediction in Support Vector Machines. J. Soft Comput. Paradig. 2019, 2019, 33–40. [Google Scholar] [CrossRef]
- Tealab, A. Time series forecasting using artificial neural networks methodologies: A systematic review. Futur. Comput. Inform. J. 2018, 3, 334–340. [Google Scholar] [CrossRef]
- Kaburlasos, V.G. FINs: Lattice Theoretic Tools for Improving Prediction of Sugar Production From Populations of Measurements. IEEE Trans. Syst. Man Cybern. Part B 2004, 34, 1017–1030. [Google Scholar] [CrossRef] [PubMed]
- Kaburlasos, V.G. The Lattice Computing (LC) Paradigm. In Proceedings of the the 15th International Conference on Concept Lattices and Their Applications CLA, Tallinn, Estonia, 29 June–1 July 2020; pp. 1–8. [Google Scholar]
- Kaburlasos, V.G.; Papadakis, S.E. Granular self-organizing map (grSOM) for structure identification. Neural Netw. 2006, 19, 623–643. [Google Scholar] [CrossRef] [PubMed]
- Kaburlasos, V.G.; Kehagias, A. Fuzzy Inference System (FIS) Extensions Based on the Lattice Theory. IEEE Trans. Fuzzy Syst. 2014, 22, 531–546. [Google Scholar] [CrossRef]
- Kaburlasos, V.G.; Athanasiadis, I.N.; Mitkas, P.A. Fuzzy lattice reasoning (FLR) classifier and its application for ambient ozone estimation. Int. J. Approx. Reason. 2007, 45, 152–188. [Google Scholar] [CrossRef] [Green Version]
- Kaburlasos, V.G.; Papakostas, G.A. Learning Distributions of Image Features by Interactive Fuzzy Lattice Reasoning in Pattern Recognition Applications. IEEE Comput. Intell. Mag. 2015, 10, 42–51. [Google Scholar] [CrossRef]
- Kaburlasos, V.G.; Papakostas, G.A.; Pachidis, T.; Athinellis, A. Intervals’ Numbers (INs) interpolation/extrapolation. In Proceedings of the 2013 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Hyderabad, India, 7–10 July 2013; pp. 1–8. [Google Scholar]
- Vrochidou, E.; Lytridis, C.; Bazinas, C.; Papakostas, G.A.; Wagatsuma, H.; Kaburlasos, V.G. Brain Signals Classification Based on Fuzzy Lattice Reasoning. Mathematics 2021, 9, 1063. [Google Scholar] [CrossRef]
- Kaburlasos, V.G.; Vrochidou, E.; Lytridis, C.; Papakostas, G.A.; Pachidis, T.; Manios, M.; Mamalis, S.; Merou, T.; Koundouras, S.; Theocharis, S.; et al. Toward Big Data Manipulation for Grape Harvest Time Prediction by Intervals’ Numbers Techniques. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020; pp. 1–6. [Google Scholar]
- Kangune, K.; Kulkarni, V.; Kosamkar, P. Automated estimation of grape ripeness. Asian J. Converg. Technol. (AJCT) 2019. Available online: https://asianssr.org/index.php/ajct/article/view/792 (accessed on 20 June 2021).
- Garnot, V.S.F.; Landrieu, L.; Giordano, S.; Chehata, N. Satellite Image Time Series Classification with Pixel-Set Encoders and Temporal Self-Attention. In Proceedings of the IEEE/CVF Conference on Computer Vision and Patern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Dupont, G.; Kalinicheva, E.; Sublime, J.; Rossant, F.; Pâques, M. Analyzing Age-Related Macular Degeneration Progression in Patients with Geographic Atrophy Using Joint Autoencoders for Unsupervised Change Detection. J. Imaging 2020, 6, 57. [Google Scholar] [CrossRef]
- Greene, W.W.H. Econometric Analysis, 7th ed.; Prentice-Hall: Hoboken, NJ, USA, 2012; ISBN 978-0-273-75356-8. [Google Scholar]
- Barra, S.; Carta, S.M.; Corriga, A.; Podda, A.S.; Recupero, D.R. Deep learning and time series-to-image encoding for financial forecasting. IEEE/CAA J. Autom. Sin. 2020, 7, 683–692. [Google Scholar] [CrossRef]
| Training | Testing | ||||
|---|---|---|---|---|---|
| Forward | Recursive | ||||
| Data | Error | Data | Error | Data | Error |
| 0.20 | |||||
| 8.53 | 13.05 | ||||
| 10.68 | 14.97 | ||||
| 12.40 | 10.61 | ||||
| 9.66 | 12.02 | ||||
| 13.54 | 19.87 | ||||
| 15.41 | 27.01 | ||||
| 15.00 | 30.48 | ||||
| 2.60 | 19.27 | ||||
| 3.27 | 21.36 | ||||
| Average | 0.20 | 10.12 | 18.74 | ||
| Standard Deviation | 0 | 4.68 | 6.82 | ||
| Training | Testing | ||||
|---|---|---|---|---|---|
| Forward | Recursive | ||||
| Data | Error | Data | Error | Data | Error |
| 2.29 | |||||
| 4.84 | 5.76 | ||||
| 4.56 | |||||
| 4.67 | 6.22 | ||||
| 1.77 | |||||
| 3.53 | 23.36 | ||||
| 2.87 | |||||
| 5.26 | 10.02 | ||||
| 2.93 | |||||
| 5.30 | 3.19 | ||||
| Average | 2.89 | 4.72 | 9.71 | ||
| Standard Deviation | 1.05 | 0.71 | 8.01 | ||
| Training | Testing | ||||
|---|---|---|---|---|---|
| Forward | Recursive | ||||
| Data | Error | Data | Error | Data | Error |
| 2.69 | |||||
| 0.77 | |||||
| 3.62 | |||||
| 1.10 | |||||
| 4.23 | 8.12 | ||||
| 3.97 | 14.48 | ||||
| 5.74 | 20.75 | ||||
| 5.73 | 24.01 | ||||
| 6.37 | 22.20 | ||||
| 8.67 | 22.34 | ||||
| Average | 2.05 | 5.78 | 18.65 | ||
| Standard Deviation | 1.34 | 1.69 | 6.12 | ||
| Training | Testing | ||||
|---|---|---|---|---|---|
| Forward | Recursive | ||||
| Data | Error | Data | Error | Data | Error |
| 3.15 | |||||
| 0.61 | |||||
| 4.71 | |||||
| 1.20 | |||||
| 1.59 | |||||
| 6.56 | 6.93 | ||||
| 7.07 | 10.15 | ||||
| 6.81 | 13.90 | ||||
| 8.12 | 11.09 | ||||
| 3.64 | 13.06 | ||||
| Average | 2.25 | 6.44 | 11.03 | ||
| Standard Deviation | 1.66 | 1.67 | 2.73 | ||
| N | Training Mode | Training Error | Testing Error (Average/Std) | |
|---|---|---|---|---|
| (Average/Std) | Forward | Recursive | ||
| 2 | (1) One sample | 0.10/0 | 11.45/9.17 | 37.87/9.96 |
| (2) Every Other sample | 3.21/1.26 | 10.54/8.74 | 17.85/11.93 | |
| (3) First Third of the samples | 5.97/3.28 | 7.92/3.43 | 18.54/4.53 | |
| (4) First Half of the samples | 5.15/3.79 | 6.84/4.12 | 7.57/4.87 | |
| 3 | (1) One sample | 0.20/0 | 10.12/4.68 | 18.74/6.82 |
| (2) Every Other sample | 2.89/1.05 | 4.72/0.71 | 9.71/8.01 | |
| (3) First Third of the samples | 2.05/1.34 | 5.78/1.69 | 18.65/6.12 | |
| (4) First Half of the samples | 2.25/1.66 | 6.44/1.67 | 11.03/2.73 | |
| 4 | (1) One sample | 0.14/0 | 14.09/3.68 | 20.21/8.92 |
| (2) Every Other sample | 1.95/0.48 | 4.99/1.95 | 9.64/4.66 | |
| (3) First Third of the samples | 0.93/0.32 | 10.85/4.25 | 25.89/2.75 | |
| (4) First Half of the samples | 1.64/0.99 | 4.30/0.96 | 6.65/2.32 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bazinas, C.; Vrochidou, E.; Lytridis, C.; Kaburlasos, V.G. Time-Series of Distributions Forecasting in Agricultural Applications: An Intervals’ Numbers Approach. Eng. Proc. 2021, 5, 12. https://doi.org/10.3390/engproc2021005012
Bazinas C, Vrochidou E, Lytridis C, Kaburlasos VG. Time-Series of Distributions Forecasting in Agricultural Applications: An Intervals’ Numbers Approach. Engineering Proceedings. 2021; 5(1):12. https://doi.org/10.3390/engproc2021005012
Chicago/Turabian StyleBazinas, Christos, Eleni Vrochidou, Chris Lytridis, and Vassilis G. Kaburlasos. 2021. "Time-Series of Distributions Forecasting in Agricultural Applications: An Intervals’ Numbers Approach" Engineering Proceedings 5, no. 1: 12. https://doi.org/10.3390/engproc2021005012
APA StyleBazinas, C., Vrochidou, E., Lytridis, C., & Kaburlasos, V. G. (2021). Time-Series of Distributions Forecasting in Agricultural Applications: An Intervals’ Numbers Approach. Engineering Proceedings, 5(1), 12. https://doi.org/10.3390/engproc2021005012









