Abstract
Aiming at the impact of machine failure on scheduling schemes in actual production, this paper proposes a multi-fidelity optimization approach considering the preventive maintenance of the machine (MOAPMM). The genetic algorithm (GA) is used as a low-fidelity model to generate a number of feasible solutions; the feasible solutions are sorted, grouped, and selected as high-quality solutions according to the EOCBA method; the high-fidelity model considering machine preventive maintenance (PM) is constructed by using the FlexSim@ software; and the high-quality solutions are simulated to obtain the optimal scheduling scheme. Experimental results show that our proposed method outperforms approaches that do not consider machine PM in terms of completion time for the flexible job shop scheduling problem with machine failure.
1. Introduction
Job shop scheduling is a critical component of machine scheduling. Classical methods like mathematical programming and branch bounding [1] face limitations in computational efficiency as the problem size increases. Swarm intelligence algorithms offer a popular approach to solving job shop scheduling problems by obtaining near-optimal solutions within a limited time frame. For example, Ali et al. [2] designed a GA based on a virtual crossover operator for the dynamic event of the random arrival of jobs, showing an improved average completion time. Demir et al. [3] combined the ant colony algorithm with GA to minimize the lead time and delay time of each job. In actual production, disturbance events such as machine failures and emergency jobs often render the original optimal solution infeasible. With the development of computer technology, simulation-based scheduling methods have been widely used. Discrete event simulation accurately represents workshop elements by creating a model close to reality. However, it is obviously too time-consuming to simulate all the scheduling schemes, and Xu et al. [4] proposed a multi-fidelity model based on ordinal transformation and optimal sampling (MO2TOS), which quickly screens high-quality solutions in low-fidelity models, samples from high-quality solutions for high-fidelity simulation, and selects the optimal solution based on the high-fidelity simulation results to reduce the computation time under the premise of guaranteeing the solution quality. Currently, there are fewer studies on high-fidelity optimization methods considering disturbance events. In this paper, we propose MOAPMM for solving flexible job shop scheduling considering machine failure.
2. Problem Description
The flexible job shop scheduling problem studied in this paper can be described as follows: there are jobs } and machines } in the workshop, each of job has operations }; each operation has its corresponding set of optional machines and is processed at different times on different machines. Consider the production reality that machines require flexible PM, i.e., the cumulative running time of the machine cannot exceed the machine maintenance threshold ; otherwise, the machine fails, and the time of post-failure maintenance (FM) is much larger than the PM time. The goal of flexible job shop scheduling is to rationally arrange each job to be processed on the machine to minimize the makespan.
The production process follows the following constraints: (1) all jobs can be processed at the initial time; (2) each machine can only process one job at a time; (3) each job cannot be processed by more than one machine at the same time; (4) there is a sequential constraint on the processes for the same job, and there is no sequential constraint on the processes for the different jobs; (5) the priority of all jobs is the same.
3. Multi-Fidelity Optimization Approach Considering Preventive Maintenance of the Machine
Multi-fidelity optimization involves a low-fidelity model (a simplified mathematical representation) and a high-fidelity model (a discrete event simulation). In this paper, we propose MOAPMM, inspired by Xu et al.’s [4] MO2TOS.
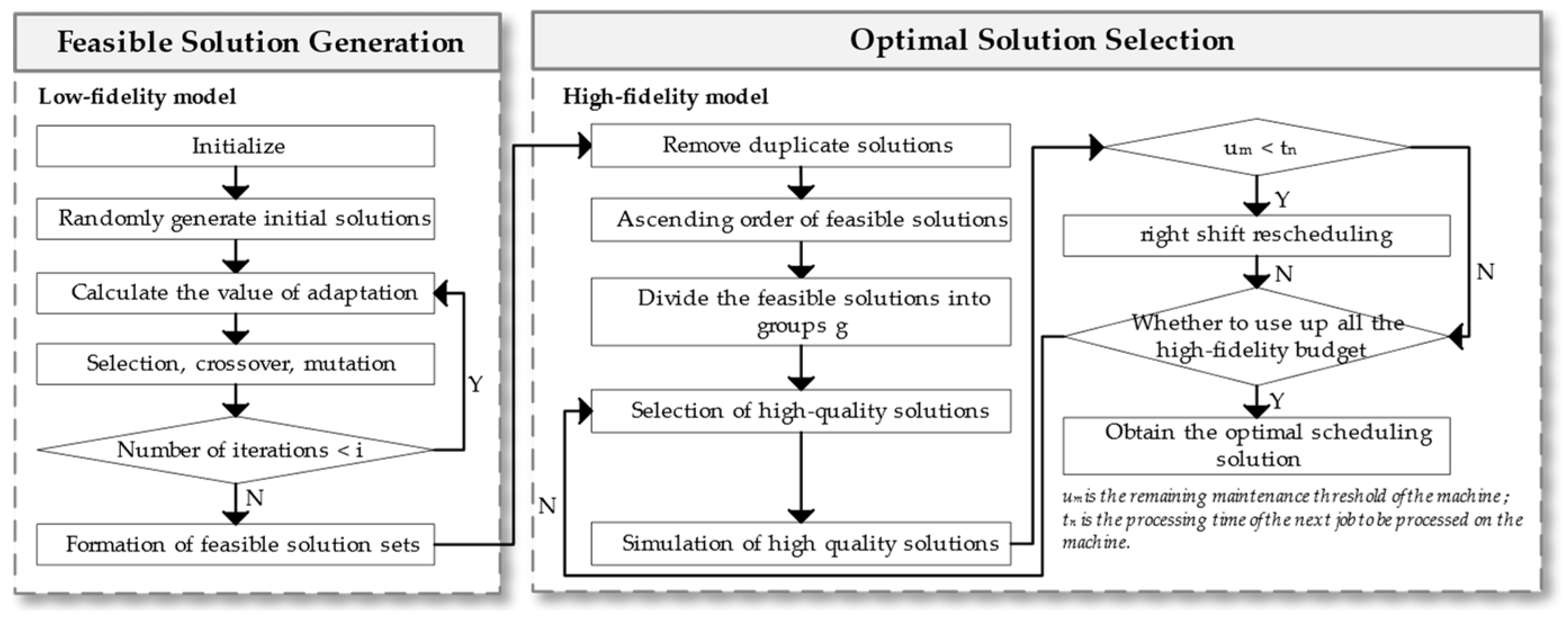
It consists of two modules: feasible solution generation and optimal solution selection. The feasible solution generation module employs a GA to quickly generate feasible solutions. The optimal solution selection module uses the Enhanced Optimal Computing Budget Allocation (EOCBA) method to select high-quality solutions; the high-fidelity simulation, considering the PM of the machine, prevents the increase in makespan caused by machine failures; and the optimal scheduling scheme is chosen from the high-quality solutions based on the simulation results. The flowchart of MOAPMM is shown in Figure 1.
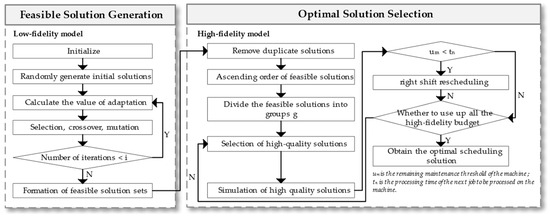
Figure 1.
Flowchart of MOAPMM.
3.1. Feasible Solution Generation
The solution space of the flexible job shop scheduling problem is large, and the mathematical model cannot get the near-optimal solution of the problem in finite time. In this paper, GA is used as a low-fidelity model to generate feasible solutions directionally through the operations of selection, crossover, and mutation, and each generation of feasible solutions is saved to the set of feasible solutions.
3.2. Optimal Solution Selection
To avoid a time-consuming simulation of all feasible solutions, it is essential to select a suitable number of high-quality solutions for simulation. Optimal Computing Budget Allocation (OCBA) is a classic approach that divides feasible solutions equally into groups and randomly selects the same number of solutions from each group for high-fidelity simulation, and each selected solution consumes a high-fidelity budget. This operation is repeated until the high-fidelity budget is exhausted.
However, this method assigns an equal probability to all feasible solutions, which may not be conducive to the selection of better solutions. In this paper, we propose the EOCBA method for high-quality solution selection. This approach considers that while high-fidelity and low-fidelity models may diverge in target values, their results are often in agreement [5]. Therefore, in accordance with a sequentially decreasing ratio, a number of solutions are chosen from each group for high-fidelity simulation, following the ratio design principle: the ratio of high-quality solutions, denoted selected from group 1 to g follows the pattern . This process is repeated until the high-fidelity budget is exhausted. If the remaining viable solutions, denoted , in a group are less than the number of solutions to be selected, the remaining unselected solutions will be included in the next group. Accordingly, the next group is required to select feasible solutions for high-fidelity simulation, where indicates the originally planned number of high-quality solutions to be selected for the next group.
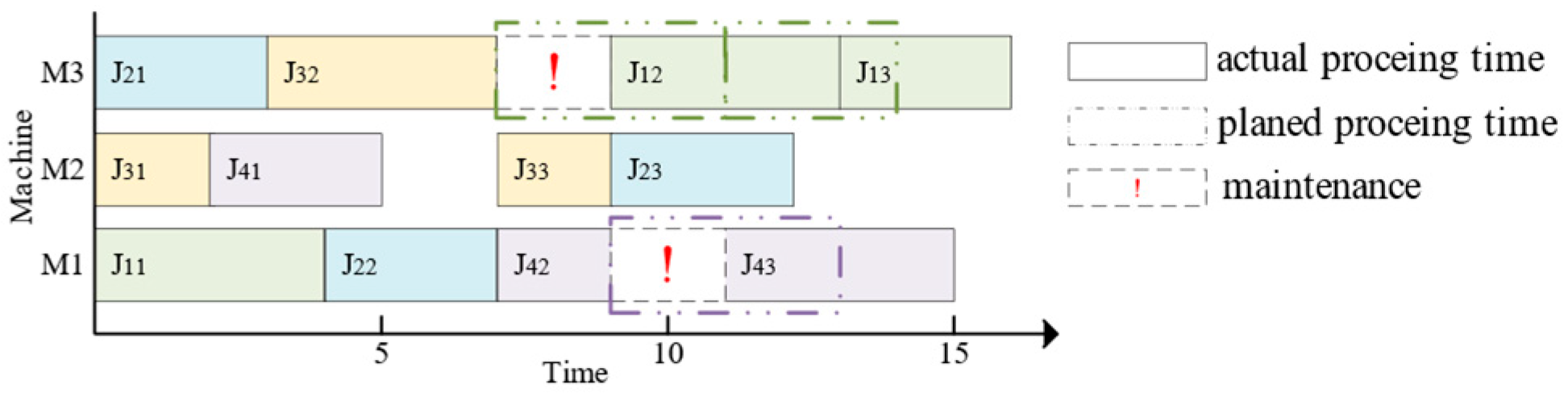
To align with actual workshop production, this paper considers the degradation of the machine’s performance over time. If not maintained quickly, the machine becomes unusable. Therefore, in high-fidelity simulation, PM of the machine is taken into account. A flexible job shop is created using flexSim@ 20.0.10, with each machine having a maintenance threshold, denoted . PM is performed before the machine’s cumulative processing time exceeds , resulting in a shorter maintenance time. Otherwise, the machine fails, resulting in longer maintenance times. When a job cannot be processed on a machine due to PM, the work is rescheduled using right shift rescheduling, as shown in Figure 2.
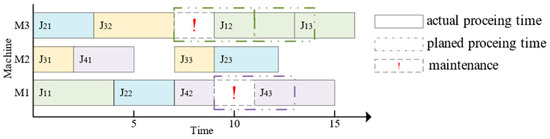
Figure 2.
Schematic of right shift rescheduling.
Supposing is 10 in Figure 2, the cumulative machining time of is 7 after finishes processing. However, since requires a processing time of 4 on , exceeds 10, triggering the need for PM. With a maintenance time of 2 units, ’s resets to 0 after maintenance. Consequently, must wait for the machine to undergo maintenance, causing a 2-unit right shift at its start processing time, and other jobs to be processed also need to be shifted to the right because the processing of jobs is subject to the conditions in Section 2.
4. Numerical Example and Analysis
4.1. Parameter Settings
In order to verify the effectiveness of the proposed method, this paper takes the two maintenance methods of PM and FM as comparison experiments in high-fidelity simulation and combines the above two groups of experiments with EOCBA and OCBA high-quality solution selection methods to form four groups of comparison experiments, and each group of experiments is carried out with different high-fidelity budgets, respectively. The budgets are strategically chosen to maximize the minimum budget required for the optimal objective value using pre-experimental data. Multiple budget sets are generated at 5-interval intervals to facilitate the process.
In this study, we conducted experiments using the literature [5] with = 8, = 4, and = 8. Set to 20, to 2, and FM time to 10, all time units are in hours. The feasible solutions are divided into five groups, and the high-quality solutions are selected for simulation from the five groups according to a ratio of 5:4:3:2:1. If the number of solutions to be selected is a non-integer calculated according to the ratio, the solutions will be selected in accordance with the rounding principle for selection.
4.2. Results Analysis
Results are presented in Table 1 based on the experiments with the given parameters.

Table 1.
Individual program performance table.
PM consistently outperforms FM in terms of performance, as shown in Table 1. By proactively considering equipment availability and reducing downtime caused by failures, PM yields superior results. Notably, both optimal solution selection methods, EOCBA and OCBA, can obtain optimal scheduling solutions, but EOCBA uses a lower high-fidelity simulation budget than OCBA, which can obtain optimal scheduling solutions faster and reduce computing time.
5. Conclusions
This study proposes MOAPMM as a solution to the flexible shop scheduling problem, considering machine failures. The method selects high-quality solutions using the EOCBA method and conducts high-fidelity simulations considering machine PM to obtain the optimal scheduling scheme. Experimental results show that this method is superior to the FM simulation method. In addition, the EOCBA method reduces the high-fidelity simulation budget and computation time while ensuring the quality of the solutions obtained.
Author Contributions
Conceptualization, L.Z. and Y.C.; methodology, L.Z. and Y.C.; software, L.Z. and J.M.; validation, L.Z. and J.M.; formal analysis, L.Z. and Y.C.; writing—review and editing, Y.C. and L.Z.; visualization, L.Z.; supervision, J.M.; funding acquisition, Y.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China grant number [No. 51705370].
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Luo, J.C.; Liu, Z.Q.; Xing, K.Y. Hybrid branch and bound algorithms for the two-stage assembly scheduling problem with separated setup times. Int. J. Prod. Res. 2019, 57, 1398–1412. [Google Scholar] [CrossRef]
- Ali, B.K.; Telmoudi, A.J.; Gattoufi, S. Improved genetic algorithm approach based on new virtual crossover operators for dynamic job shop scheduling. IEEE Access. 2020, 8, 213318–213329. [Google Scholar] [CrossRef]
- Demir, H.I.; Erden, C. Dynamic integrated process planning, scheduling and due-date assignment using ant colony optimization. Comput. Ind. Eng. 2020, 149, 106799. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, S.; Huang, E.; Chen, C.H.; Lee, L.H.; Celik, N. MO2TOS: Multi-fidelity optimization with ordinal transformation and optimal sampling. Asia. Pac. J. Oper. Res. 2016, 33, 1650017. [Google Scholar] [CrossRef]
- Wang, J.; Liu, Y.; Ren, S.; Wang, C.; Ma, S.Y. Edge computing-based real-time scheduling for digital twin flexible job shop with variable time window. Robot. Comput.-Integr. Manuf. 2023, 79, 102435. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).