Abstract
Hot forming of aluminium sheets enables the forming of complex shapes with high-strength alloys due to increased formability at elevated temperatures. A fast, uniform and accurate heating method is required to meet the narrow solution heat treatment window from 460 to 490 °C for AA7xxx alloys before forming. Heated plates and convection furnaces are commonly used in hot forming, but require large equipment and can have medium to long cycle times. Induction heating, which uses an alternating current in a coil surrounding the workpiece, could provide shorter heating times. However, induction heating requires a part-specific coil and can exhibit significant temperature gradients over the blank. Multi-physics electromagnetic and thermal simulation can be used as a design tool to help achieve the target temperature uniformity. In this study, induction heating of an irregular aluminium blank was modelled and validated with experimental data. Methods to improve the temperature uniformity were also tested numerically.
1. Introduction
Elevated temperature forming processes for aluminium alloys have received much attention in the past 20 years since they can greatly increase the formability of aluminium alloys and enable complex sheet metal components to be formed, for instance for the automotive sector. Different temperature ranges have been considered for different purposes, such as warm forming around 250 °C for AA5xxx-O inner doors [1], warm forming around 200 °C for heat-treatable high-strength AA7xxx [2], hot forming around 500 °C for superplastic AA5xxx alloys [3] and more recently hot-form, die-quench processes for high-strength AA6xxx and AA7xxx that provide lightweighting opportunities in the automotive industry [4,5,6,7].
One common requirement for these processes is that aluminium blanks, often with large dimensions, need to be uniformly heated to the target temperature. In industrial applications, there is also a need for fast heating cycles to meet the productivity requirements. Hot-form, die-quench processes can be used to manufacture high-strength AA7xxx-Tx with a yield strength exceeding 500 MPa. In this process, blanks are first heated up and held at their solution heat treatment temperature of the order of 480 °C to dissolve alloying elements and, in some case, partially recrystallize the as-rolled microstructure. Blanks are then quickly transferred to a cold die and stamped to form and quench the component, which is finally heat treated to achieve the target properties. One challenge for such materials is the relatively narrow solution heat treatment window that must be achieved throughout the blank for consistent final properties. Too low a temperature would not sufficiently dissolve the elements, and too high a temperature could lead to local incipient melting [7].
Multiple heating methods have been implemented alone or in combinations for hot-forming processes, including conduction-based hot plates [1,3], batch or continuous convection furnaces powered by gas or electricity [5,8], resistive heating [2,9], infrared heaters [10] as well as electromagnetic induction heating [6,11,12,13,14,15]. The latter uses a high-frequency alternating current through a conducting coil to heat up the metal sheet through eddy currents and the Joule effect. Some advantages of the method are fast heating times, depending on the available power which can reach 100 kW and above, and that only the blank heats up while the coil is liquid-cooled to near ambient temperature. For instance, fast heating times can be beneficial when solutionizing some aluminium alloys to control the precipitation and possible grain growth response [16] and can also reduce the holding time required. On the other hand, each blank shape can require a specific coil that must be matched with the power source for optimal efficiency. Coil design and fabrication can therefore become time consuming for complex parts.
In the past decade, commercial simulation software such as LS-Dyna®, COMSOL® and DEFORM have followed the development of experimental methods to model the complex electromagnetic, thermal, fluid and mechanical interactions involved in induction heating [17,18,19,20,21]. Multi-physics modelling has already been used to investigate different longitudinal and transverse coil design strategies [14,20,22,23] and geometrical effects such as around cutouts [14,17], with sometimes limited experimental validation of the models. On the other hand, temperature optimization work has focused on physical trials, using adjustments or devices such as flux concentrators to manage the electromagnetic interactions [6,24,25].
The purpose of this work was therefore first to test and validate an electromagnetic induction heating model using experimental trials with an irregular AA7075 aluminium sheet, and then to numerically test possible design variations that could be efficiently implemented to make the temperature distribution more uniform.
2. Induction Heating
Electromagnetic induction heating is governed by the interactions of electric and magnetic fields in the coil and workpiece, expressed by the Maxwell equations. An alternating current flowing through a conductor generates a time-varying magnetic field around it, and the changing magnetic field creates electrical currents, called eddy currents, in conductors. Eddy currents then generate heat within the part through the Joule effect.
Currents are concentrated at the surface of the workpiece, a phenomenon called the skin effect, which means that the surface of the part receives a higher specific heat input. The penetration depth δ, which refers to the depth at which the current density drops below approximately 37% or the surface current density, is expressed as:
where ρ is the specific electrical resistivity of the workpiece, µ0 is the magnetic permeability of vacuum, µr is the relative permeability of the workpiece material and f is the current frequency. Electrical properties also vary with temperature, but unlike steel, aluminium alloys do not encounter a drastic change in relative permeability due to phase changes. As the current density varies through the thickness, Joule heating is also concentrated close to the surface.
In practice, the induction coil is designed to match the workpiece as well as the high-frequency generator (in the range of kHz to MHz). To efficiently generate the oscillating current, the generator uses a capacitor bank with a capacitance C to create a resonant tank circuit where the charge moves back and forth. In the resonant circuit, the induction coil is the inductance element and the inductance L value depends on the coil-enclosed area, length, and number of turns. The power generator is therefore tuned close to the resonant frequency:
3. Methods
3.1. Experimental Methods
The test case investigated is a trapezoidal AA7075 aluminium alloy blank with dimensions of approximately 200 × 500 mm and a thickness of 2.8 mm. For the target application, the objective was to achieve a temperature of 480 °C as uniformly as possible over the surface of the sheet during the holding time.
The trials used a 50 kW generator with non-contact closed-loop temperature control and designed for a frequency of approximately 20 kHz and an internally cooled ¼ inch copper tubing coil with a nearly rectangular enclosed area cast into insulating cement. The longitudinal field configuration was selected for uniformity and was suitable for the relatively thick aluminium sheet used for a prototype structural automotive component. The experimental setup is shown in Figure 1a.
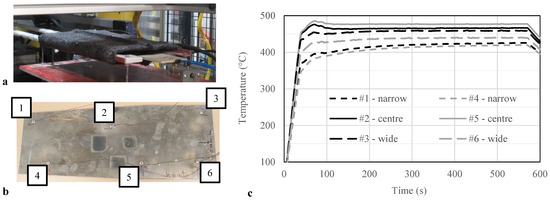
Figure 1.
Experimental setup, (a) Longitudinal flux induction heating coil used in trials, (b) test blank with thermocouples, (c) Example heat-up profile.
Six K-type thermocouples were installed on a blank by clamping with rivets, as shown in Figure 1b, and temperature profiles were recorded during heating to the target temperature. An example heat-up profile is shown in Figure 1c: in this instance the control tuning lead to a fast heat-up and minimal overshoot of the order of 5 °C.
3.2. Induction Heating Model
A simplified model of the experimental setup was prepared on the Altair® and LS-Dyna® (version 10.1.0) platforms with a focus on the steady-state regime, as illustrated in Figure 2. Only the aluminium blank and copper coil were included in the model and both were discretized as brick elements.
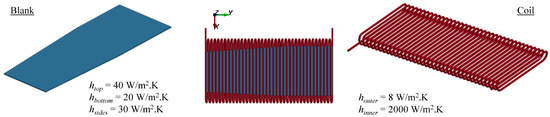
Figure 2.
Blank and coil geometries included in the model.
LS-Dyna® uses the boundary element method for the air volume between the blank and coil and the finite element method within the conductors. In induction heating simulations, the electromagnetic interaction typically requires the most computation time. For this reason, the solver dedicated to induction heating applications first calculates the electromagnetic response over a very short duration of one current period (1/f) and propagates a constant heat input field to the thermal solver over a longer “macro” period [21]. To further simplify the model, the workpiece geometry was taken as a rigid body with the final shape including its thermal expansion so that the volume of the parts did not vary over time, allowing a single solution to the boundary element problem. Similarly, while the solver accepts temperature-dependent electromagnetic and thermal properties for the conductors [18], constant estimated properties were used for the blank and coil and are summarized in Table 1. The temperature dependence of electrical and thermal properties was not accounted for herein. The electromagnetic boundary condition was applied in terms of a sinusoidal applied voltage difference between coil leads. The voltage amplitude was manually and iteratively adjusted to approach the target temperature; the relationship between voltage and maximum temperature was approximately quadratic. The inner surface of the hollow tube was removed from the boundary element solution.

Table 1.
Material properties assumptions in electromagnetic–thermal model.
Heat exchange between the hot blank and the surrounding environment is also a complex problem, especially with the blank being placed on supports in a tubular channel. In this work, boundary conditions for the blank and coil were simplified to constant, estimated convection heat transfer coefficients and an ambient environment temperature as summarized in Figure 2 and sensitivity of the results to the heat transfer coefficients was assessed. Radiation heat transfer and conduction between the blank and its insulating support (not included in the model) were omitted; radiation is generally less significant in the temperature range in this study [21]. While a steady-state solution would be sufficient for the holding regime, a transient solution was conducted herein.
A sensitivity study of the numerical effects was first conducted to assess the influence of solver choices and mesh dimensions in plane and through thickness. Comparisons were made in terms of temperature extrema on the blank. Comparisons were then made between predicted and measured temperatures at thermocouple locations with the selected mesh configuration. Finally, geometrical variations of the coil were prepared to reduce the predicted spread of temperature on the blank, which would be beneficial for optimal mechanical properties in hot-stamped high-strength 7xxx aluminium sheets.
4. Results and Discussion
4.1. Numerical Sensitivity
First, for a baseline mesh, the iterative and direct solution methods available in LS-Dyna® were tested and compared. While the temperature solutions were consistent with proper iterative solver tolerances, differences in memory usage and computation time (for a single CPU) were noted as shown in Table 2. The direct solution required significantly less time at the expense of memory usage and was selected for the remainder of the simulations conducted on an HP workstation with Intel Xeon® E5 processors and 512 GB RAM. The compromise between computation time and memory for specific computer configurations could be a factor towards automated, iterative coil design for minimizing the temperature variation in the workpiece.

Table 2.
Simulation cost for direct and iterative solvers.
The predicted temperatures with varying mesh sizes are provided in Table 3 for a fixed input voltage amplitude. The temperature range between the minimum and maximum nodal values is 56 °C for the baseline mesh # 1. Temperatures decrease most significantly and the range is reduced by 2 °C with the coarser through-thickness surface element size in # 3 and 4, which is likely due to a less accurate discretization of the through-thickness current gradient associated with the skin effect. For comparison, the skin depth δ for aluminium at the experimental frequency is approximately 0.6 mm based on Equation (1). A biased mesh with thinner elements at the surface is therefore preferred. Coarser in-plane blank elements reduced the temperature slightly whereas a coarser coil mesh increased it, but the differences were less than 2% and mesh type # 1 was retained for the following analyses. Further refinement may, however, be required in the presence of cutouts where edge effects could be important [14,20].

Table 3.
Mesh configurations and predicted temperatures.
4.2. Comparison to Experiments
Using mesh type # 1 in Table 3, the predicted temperature profiles at the thermocouple locations are shown in Figure 3. Due to the relatively large coil height, narrow pitch and high thermal conductivity of the aluminium workpiece, no significant temperature gradient was predicted between the turns. The model correctly predicted higher temperature at the longitudinal centre, but there were discrepancies for some of the end points as summarized in Table 4. The significant difference in ramp-up rate and shape is due to the closed-loop control in the experiments, while simulations used a constant heating power leading to an asymptotic approach to a steady state where energy input from inductive heating balanced heat losses to the environment. Simulating closed-loop power control would however increase the computational cost due to additional electromagnetic solution increments and was not attempted in this study.
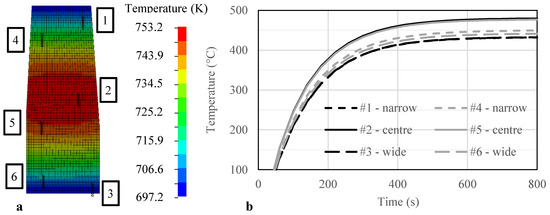
Figure 3.
Predicted temperature with the “reference” model, mesh type # 1, (a) near-stable field, 1–6 (see Figure 1b), (b) heat-up profile over time at experimental thermocouple locations.

Table 4.
Calculated and measured temperatures in steady-state regime.
Considering that the coil was just long enough to match the thermally expanded blank length, one possible explanation could be that the blank was not perfectly centered along the y (length) axis within the coil in the experiments. Table 4 shows the predicted temperatures assuming that the blank was offset 5 mm towards the narrow end. The temperature dropped significantly at the narrow end (# 1 and 4) beyond the coil footprint, which highlights the importance of repeatable positioning.
The hypothesis above cannot fully explain the temperature discrepancy between the simulations and the experimental data shown in Figure 2. Given the challenge of accurately forming a copper coil, small local geometrical variations (see Section 4.3) could have played a role, especially at measurement locations # 3 and 4 that did not correlate well. Nevertheless, the model can provide a good indication of the temperature variations and can be used at least in a qualitative sense to optimize the coil design for improved temperature uniformity.
Simulations have also shown that lower heat transfer coefficients between the blank and the environment tend to decrease the temperature gradient in the sheet, as summarized in Table 5. Conversely, underestimated convection coefficients would translate to too small a temperature difference; contact conduction losses to the supports could have a similar effect. In practice, minimizing convection losses would be beneficial to temperature uniformity, in addition to reducing the power requirement during holding.

Table 5.
Calculated inductance and temperatures for different model configurations.
4.3. Coil Modifications for Temperature Uniformity
The temperature gradients predicted in the previous section would lead to less-than-optimal properties in some regions of an AA7075 part after forming and heat treatment, especially close to the ends. There is therefore an interest in modifying a coil design to reduce the gap between the highest and lowest temperatures. Three variations illustrated in Figure 4 were tested numerically while keeping the same number of turns. Results in terms of inductance, temperature range and applied voltage are presented in Table 5.
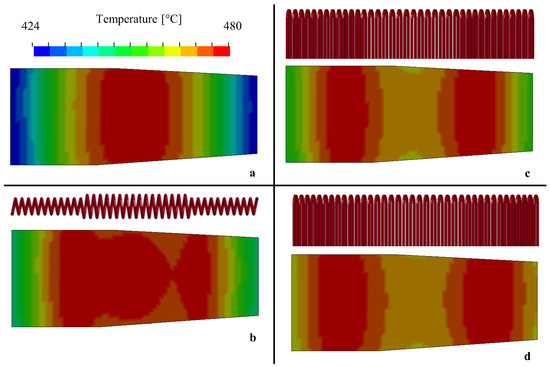
Figure 4.
Calculated steady-state temperature distributions for (a) uniform coil, (b) variable height coil, (c) three-section variable pitch coil and (d) turn-by-turn variable pitch coil.
Varying the height of the turns can be used to control the relative heating efficiency (Figure 4b). By increasing the height and coupling distance at the centre, the energy transfer was reduced locally [12]. This increased the required voltage for the same maximum temperature and significantly increased the coil inductance, which could fall outside the generator’s optimal range. Reducing the height would have been another option, but clearances were required to handle the sheet [6].
In practice, altering the coil pitch is more practical for fast modifications, especially in final experimental adjustments, since the copper tube length remains essentially the same. In addition, the inductance varies much less while achieving the same improvement in temperature uniformity. Incremental improvements can be gained by adjusting each turn spacing individually (Figure 4d) compared to a three-zone design (Figure 4c); this was conducted in this work by manually shifting the mesh with relative displacements between turns of the order of 1 mm. While manual iterations already showed notable reduction of the predicted temperature range, morphing automation and optimization algorithms could be used to automatically generate a favourable coil design.
5. Conclusions
In this work, the electromagnetic–thermal coupled solvers of the commercial solver LS-Dyna® were used to build and validate an induction heating model for aluminium alloy sheets towards hot stamping applications. While discrepancies remained compared to some of the experimental results, modelling can provide guidance when designing a new coil. Firstly, calculated inductances can be used as an initial guideline for matching the generator frequency by adjusting the number of turns, for instance by comparison with prior successful coils. Secondly, strategies can be tested to improve the temperature uniformity [22]. Further development could also lead to validation of the power requirement for new parts with existing generators, which was not addressed in this work.
Some numerical and experimental challenges remain. The modelling of thermal losses could be improved, through further experimental measurements or fluid flow simulation, to improve the reliability of the predicted temperature gradient since this was shown to be a factor. In practice, building a hand-made, meter-long tubing coil with guide jigs to millimetre accuracy can be a challenge, which could result in local temperature changes that can only be measured with non-local measurements such as with an infrared camera. Simulation and experimental work is also underway to test induction heating of a complex-shape aluminium alloy blank.
Induction heating is an attractive tool in the laboratory to rapidly change heating parameters in tensile or forming test series, as there is no thermal inertia in the system. On the other hand, it may be difficult to achieve production cycle times without a number of parallel induction heating systems, which could become expensive compared to conventional furnaces.
While the objective remains to minimize the temperature gradient for optimal properties after aging in aluminium hot stamping, the calculated temperature field could be used as an input in forming simulations in instances where some temperature gradients remain, since formability is dependent upon temperature [26]. As developed for boron steel hot stamping in part due to heating efficiency loss beyond the Curie temperature [14], a sequence of induction and furnace heating [6] could be implemented for fast heating times and temperature uniformity for very complex blank shapes that would require correspondingly complex induction heating coils.
Author Contributions
Conceptualization, G.D. and A.G.; methodology, G.D. and A.G.; software, A.G.; validation, G.D.; formal analysis, A.G.; data curation, G.D.; writing—A.G.; writing—review and editing, A.G. and G.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data used in this study are confidential and are kept as proprietary information by the METALTec industrial research and development group.
Acknowledgments
The authors acknowledge the contributions of the NRC team who participated in the various aspects of this study: Philippe Tremblay, Alexandre Morin and Xavier Tremblay. This work was carried out using experimental data from the “Alloy and Process Development for the High Productivity Production of Aluminium Hot-Stamped Lightweight Structural Components” project that was supported by the NRC’s METALTec industrial R&D group members and sponsors as well as the NRC’s Advanced Manufacturing Program and the Canadian Program for Energy Research and Development.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Harrison, N.R.; Ilinich, A.M.; Friedman, P.A.; Singh, J. Optimization of high-volume warm forming for lightweight sheet. In Proceedings of the SAE 2013 World Congress & Exhibition, Detroit, MI, USA, 16–18 April 2013. [Google Scholar]
- Ivanoff, T.A.; Taleff, E.M.; Hector, L.G., Jr. Warm forming of AA7075-T6 with direct electrical resistance heating. In Light Metals 2015; Hyland, M., Ed.; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Saito, K.; Watanabe, J.; Yokoyama, O.; Nakao, K. Application technology of aluminum blow forming for automotive closure panel. In Proceedings of the EuroSPF 2008, Carcassonne, France, 3–5 September 2008. [Google Scholar]
- Garrett, R.P.; Lin, J.G.; Dean, T.A. Solution heat treatment and cold die quenching in forming AA 6xxx sheet components: Feasibility study. Adv. Mater. Res. 2005, 6–8, 673–680. [Google Scholar] [CrossRef]
- Harrison, N.R.; Luckey, S.G. Hot stamping of a B-pillar outer from high strength aluminum sheet AA7075. SAE Int. J. Mater. Manuf. 2014, 3, 567–573. [Google Scholar] [CrossRef]
- Politis, D.; Li, N.; Wang, L.; Lin, J. An Industrial System Enabling the Use of a Patented, Lab-Proven Materials Processing Technology for Low Cost Forming of Lightweight Structures for Transportation Industries; Imperial College London: London, UK, 2017. [Google Scholar]
- Samuel, E. Application of the hot stamping process to aluminum alloy structural components. In Light Metals 2018; TMS 2018; Martin, O., Ed.; Springer: Cham, Switzerland, 2018; pp. 301–306. [Google Scholar]
- Shao, Z.; Jiang, J.; Lin, J. Feasibility study on direct flame impingement heating applied for the solution heat treatment, forming and cold die quenching technique. J. Manuf. Process. 2018, 36, 398–404. [Google Scholar] [CrossRef]
- Liang, W.; Wang, L.; Liu, Y.; Wang, Y.; Zhang, Y. Hot stamping parts with tailored properties by local resistance heating. In Proceedings of the 11th International Conference on Technology of Plasticity, Nagoya, Japan, 19–24 October 2014; pp. 1731–1736. [Google Scholar]
- Mauduit, D.; Le Fournier, M.; Grondin, K.; Pottier, T.; Le-Maoult, Y. Industrial applications of the superplastic forming by using infra-red heater. In Proceedings of the 12th International Conference on the Technology of Plasticity, ICTP 2017, Cambridge, UK, 17–22 September 2017. [Google Scholar]
- Karbasian, H.; Tekkaya, A.E. A review on hot stamping. J. Mater. Process. Technol. 2010, 210, 2103–2118. [Google Scholar] [CrossRef]
- Kolleck, R.; Veit, R.; Merklein, M.; Lechler, J.; Geiger, M. Investigation on induction heating for hot stamping of boron alloyed steels. CIRP Ann.-Manuf. Technol. 2009, 58, 275–278. [Google Scholar] [CrossRef]
- Zimin, L.S.; Sorokin, A.G.; Egiazaryan, A.S.; Filimonova, O.V. Systematic approach to optimal design of induction heating installations for aluminum extrusion process. In Proceedings of the International Conference on Mechanical Engineering, Automation and Control Systems, Tomsk, Russia, 4–6 December 2017; Volume 327. [Google Scholar]
- Nacke, B.; Dietrich, A. Potentials of single stage induction heating for press hardening of steel blanks. In Proceedings of the 9th International Symposium on Electromagnetic Processing of Materials, Hyogo, Japan, 14–18 October 2018; p. 5. [Google Scholar]
- Kim, D.K.; Woo, Y.Y.; Park, K.S.; Sim, W.J.; Moon, Y.H. Advanced induction heating system for hot stamping. Int. J. Adv. Manuf. Technol. 2018, 99, 583–593. [Google Scholar] [CrossRef]
- Li, N.; Zheng, J.; Zhang, C.; Zheng, K.; Lin, J.; Dean, T.A. Investigation on fast and energy-efficient heat treatments of AA6082 in HFQ processes for automotive applications. In Proceedings of the 4th International Conference on New Forming Technology, Glasgow, UK, 6–9 August 2015; p. 7. [Google Scholar]
- Jankowski, T.A.; Johnson, D.P.; Jurney, J.D.; Freer, J.E.; Dougherty, L.M.; Stout, S.A. Experimental observation and numerical prediction of induction heating in a graphite test article. In Proceedings of the COMSOL Conference, Boston, MA, USA, 30 March 2009. [Google Scholar]
- L’Eplattenier, P.; Çaldichoury, I.; Anton, J. LS-DYNA R7: Update on the electromagnetism module (EM). In Proceedings of the 9th European LS-DYNA Conference, Manchester, UK, 2–4 June 2013. [Google Scholar]
- Lilja, M. Electromechanics in LS-DYNA R7. In Proceeding of Nordic LS-Dyna ANSA Information Day, Göteborg, Sweden, 26 September 2013. [Google Scholar]
- Tian, Y.; Wang, L.; Anyasodor, G.; Qin, Y. Numerical study of the induction heating of aluminium sheets for hot stamping. In Proceedings of the International Conference on New Forming Technology, Bremen, Germany, 18–21 September 2018; p. 6. [Google Scholar]
- Grippon, E.; Senart, T.; Lapoujade, V. Evaluation of electromagnetism capabilities of LS-DYNA: Alternative heating processes. In Proceedings of the 10th European LS-DYNA Conference, Würzburg, Germany, 15–17 June 2015; p. 10. [Google Scholar]
- Bao, L.; Chen, J.; Li, Q.; Gu, Y.; Wu, J.; Liu, W. Research on a new localized induction heating process for hot stamping steel blanks. Materials 2019, 12, 1024. [Google Scholar] [CrossRef] [PubMed]
- Tian, Y.; Wang, L.; Anyasodor, G.; Xu, Z.; Qin, Y. Heating schemes and process parameters of induction heating of aluminium sheets for hot stamping. Manuf. Rev. 2019, 6, 17. [Google Scholar] [CrossRef]
- Anderhuber, M.; Chaignot, J.P.; Couffet, C.; Hellegouarc’h, J.; Paya, B.; Pierret, R.; Neau, Y.; Uring, J.C.; Pateau, O.; Griffay, G.; et al. Transverse Flux Induction Heating Device with Magnetic Circuit of Variable Width. U.S. Patent US6,498,328 B2, 24 December 2002. [Google Scholar]
- Woods, E. Method for Improving Thermal Uniformity in Induction Heating Processes. U.S. Patent US6,091,063, 18 July 1998. [Google Scholar]
- D’Amours, G.; Ilinich, A. High temperature characterization and material model calibration for hot stamping of AA7075 aluminium sheet. In Proceedings of the International Deep Drawing Research Group 37th Annual Conference, Waterloo, ON, Canada, 3–7 June 2018; p. 8. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).