Dynamic Tikhonov State Forecasting Based on Large-Scale Deep Neural Network Constraints †
Abstract
1. Introduction
2. Materials and Methods
2.1. Forward Dynamic Problem
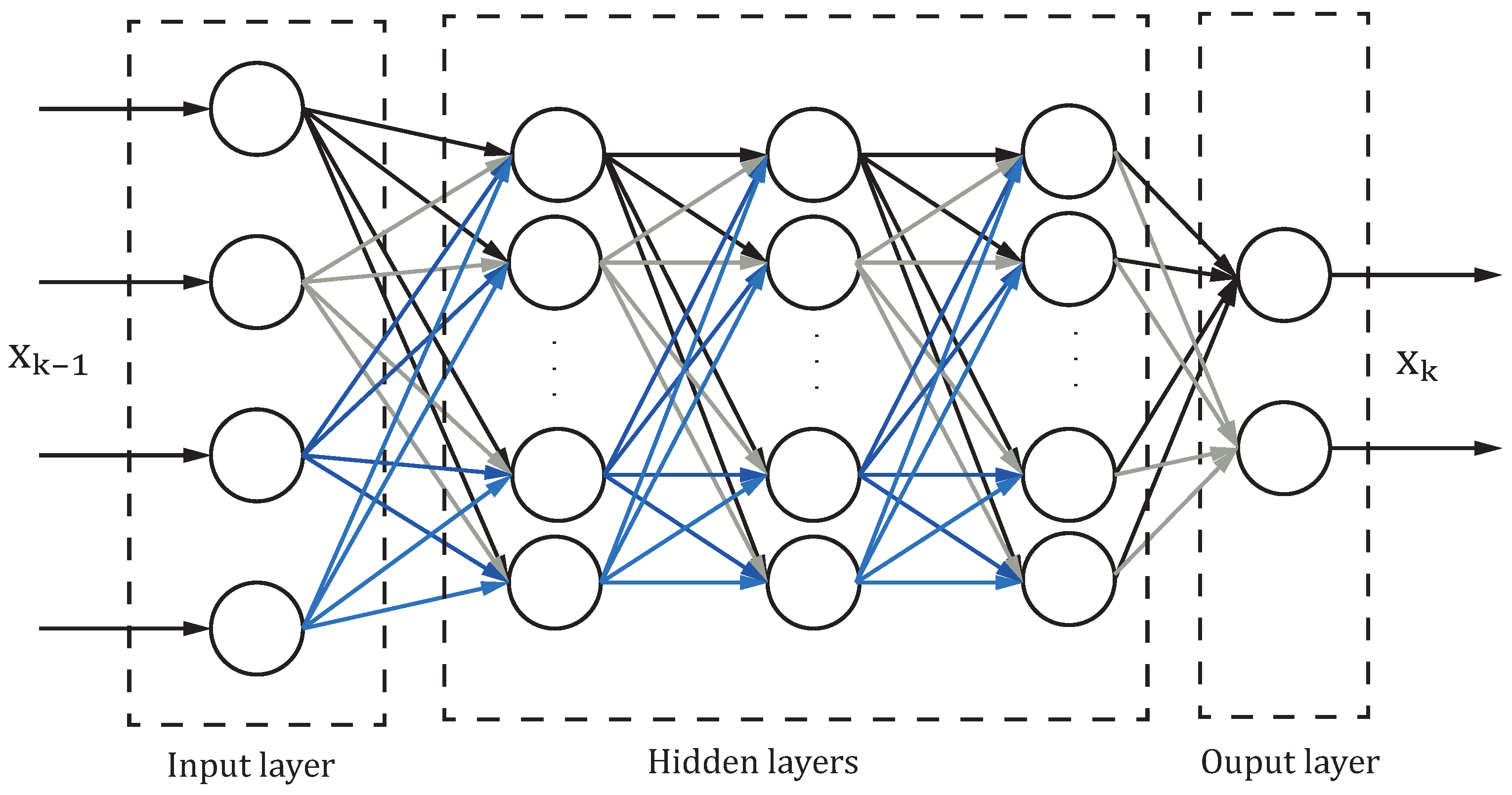
2.2. Dynamic Tikhonov Based on DNN
3. Results
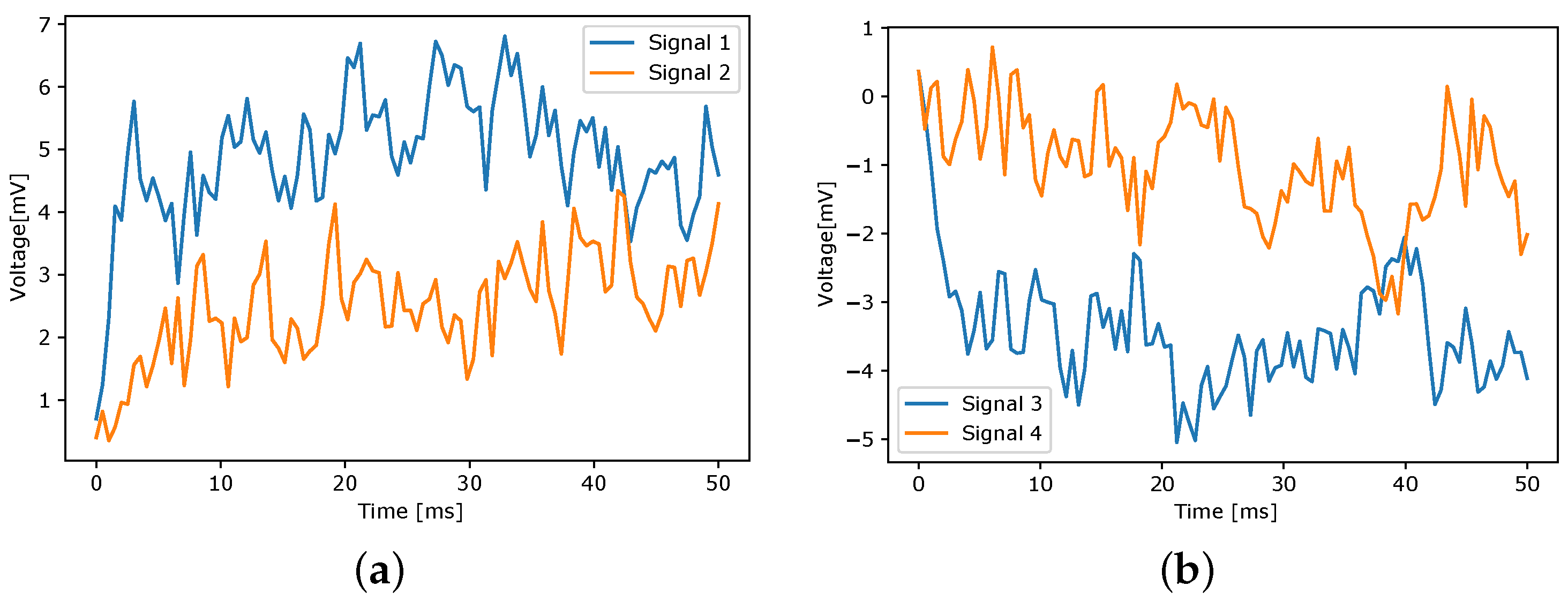
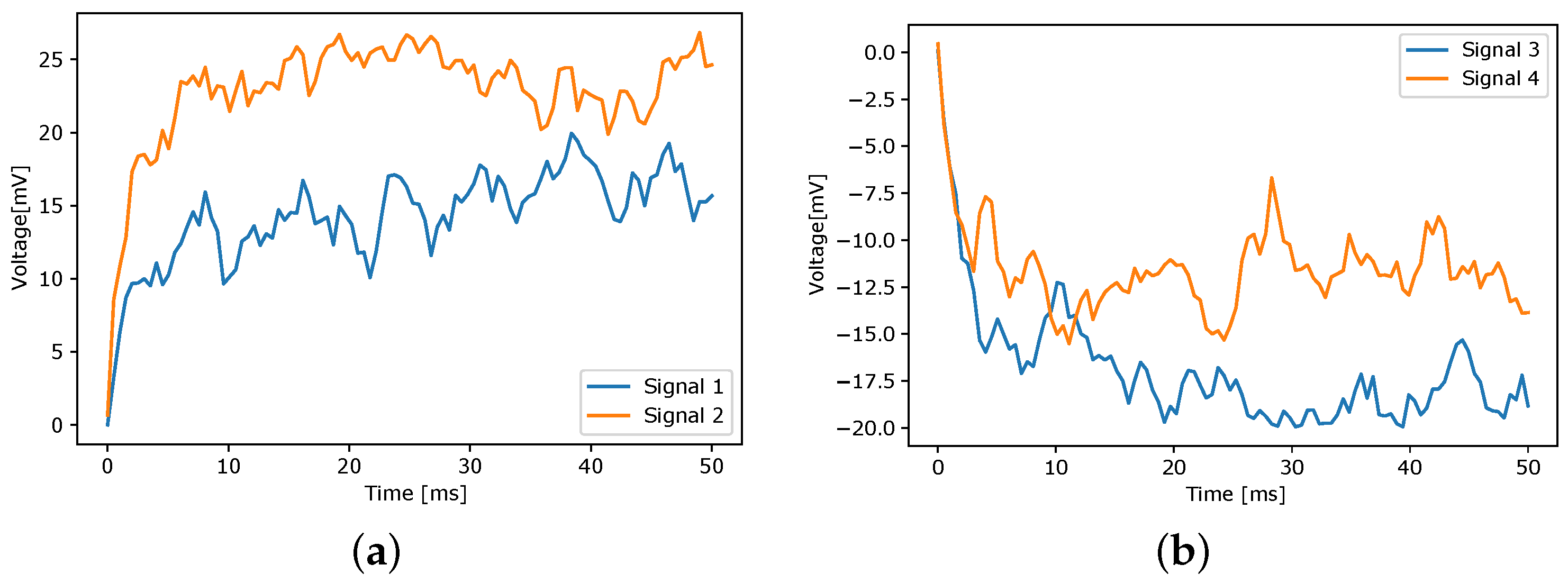
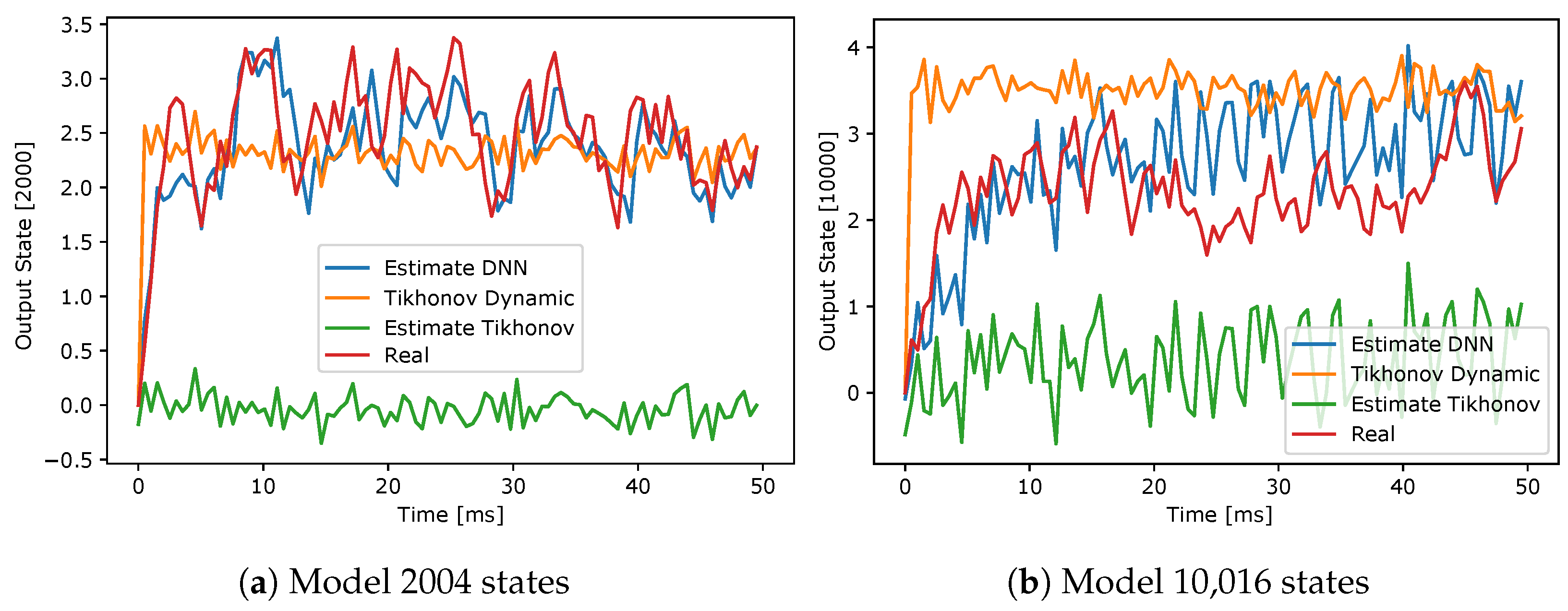
3.1. Experimental Setup
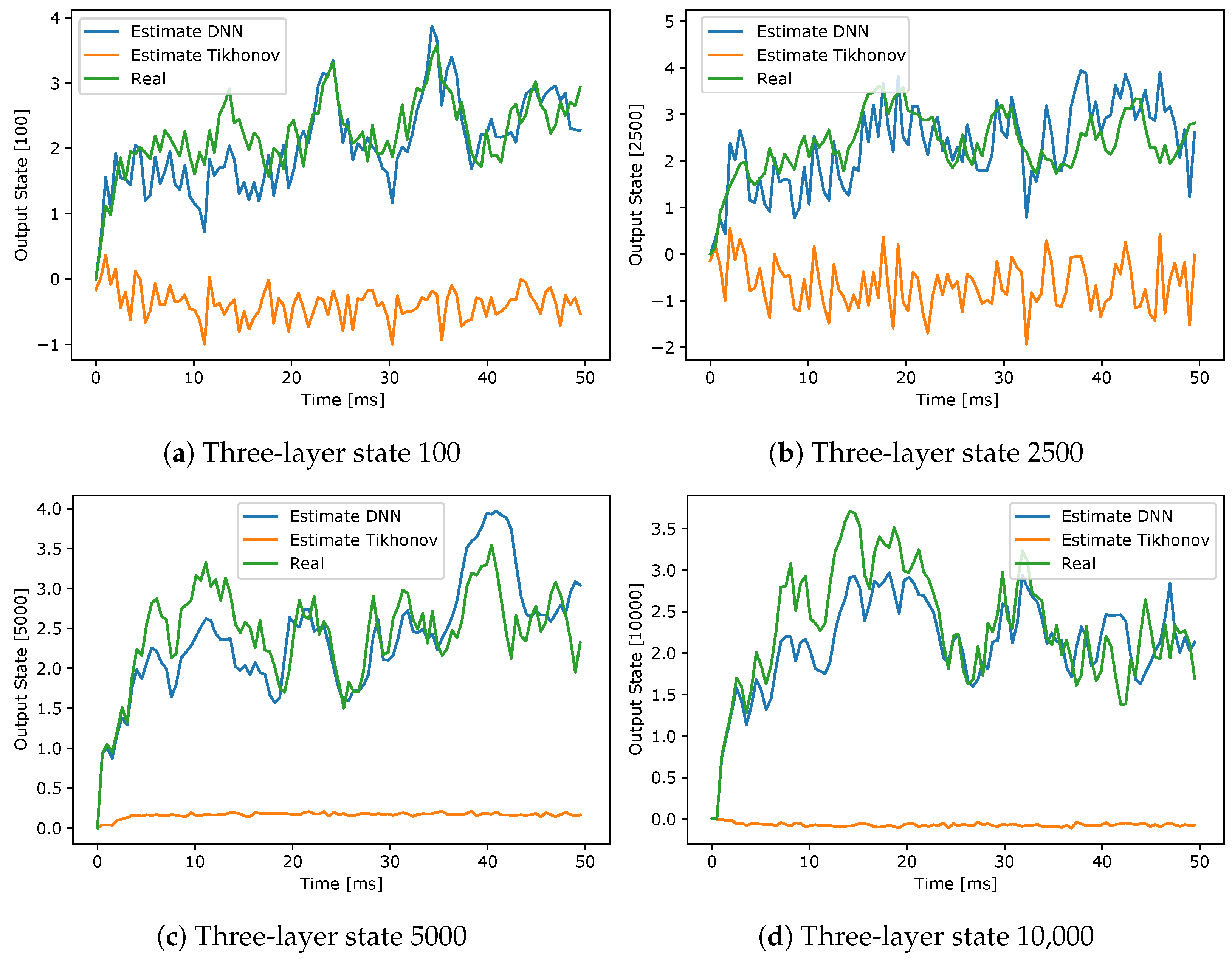
3.2. State Forecasting Results
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, K.; Zuo, W.; Chen, Y.; Meng, D.; Zhang, L. Beyond a gaussian denoiser: Residual learning of deep CNN for image denoising. IEEE Trans. Image Process. 2017, 26, 3142–3155. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Schwab, J.; Antholzer, S.; Haltmeier, M. Nett: Solving inverse problems with deep neural networks. Inverse Probl. 2020, 36, 065005. [Google Scholar] [CrossRef]
- Zhang, Z.; Brand, M. Convergent block coordinate descent for training tikhonov regularized deep neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Chien, J.T.; Lu, T.W. Tikhonov regularization for deep neural network acoustic modeling. In Proceedings of the 2014 IEEE Spoken Language Technology Workshop (SLT), South Lake Tahoe, NV, USA, 7–10 December 2014; pp. 147–152. [Google Scholar]
- Afkham, B.M.; Chung, J.; Chung, M. Learning regularization parameters of inverse problems via deep neural networks. Inverse Probl. 2021, 37, 105017. [Google Scholar] [CrossRef]
- Nguyen, H.V.; Bui-Thanh, T. Tnet: A model-constrained tikhonov network approach for inverse problems. arXiv 2021, arXiv:2105.12033. [Google Scholar]
- Romano, Y.; Elad, M. The little engine that could: Regularization by denoising (red). In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Mao, X.J.; Shen, C.; Yang, Y.B. Image restoration using very deep convolutional encoder-decoder networks with symmetric skip connections. In Proceedings of the European Conference on Computer Vision (ECCV), Amsterdam, The Netherlands, 11–14 October 2016. [Google Scholar]
- Kolowrocki, K. 10—Large complex systems. In Reliability of Large and Complex Systems; Elsevier: Amsterdam, The Netherlands, 2014; Volume 2. [Google Scholar]
- Sockeel, S.; Schwartz, D.; Pélégrini-Issac, M.; Benali, H. Large-scale functional networks identified from resting-state EEG using spatial ICA. PLoS ONE 2016, 11, e0146845. [Google Scholar] [CrossRef] [PubMed]
- Sanchez-Bornot, J.M.; Sotero, R.C.; Kelso, S.; Coyle, D. Solving large-scale meg/EEG source localization and functional connectivity problems simultaneously using state-space models. arXiv 2022, arXiv:2208.12854. [Google Scholar]
- Wang, Q.; Loh, J.M.; He, X.; Wang, Y. A latent state space model for estimating brain dynamics from electroencephalogram (EEG) data. Biometrics, 2022; Early View. [Google Scholar] [CrossRef]
- Giraldo-Suarez, E.; Martinez-Vargas, J.D.; Castellanos-Dominguez, G. Reconstruction of neural activity from EEG data using dynamic spatiotemporal constraints. Int. J. Neural Syst. 2016, 26, 1650026. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Parra, L.C.; Haufe, S. The new york head—A precise standardized volume conductor model for EEG source localization and tes targeting. NeuroImage 2016, 140, 150–162. [Google Scholar] [CrossRef] [PubMed]




| Model | Regularized LS Model 2 K | Regularized LS Model 10 K |
|---|---|---|
| Hidden Layers | Regularized LS-DNN Model 2 K | Regularized LS-DNN Model 10 K |
|---|---|---|
| 0 | ||
| 1 | ||
| 2 | ||
| 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Molina, C.; Martinez, J.; Giraldo, E. Dynamic Tikhonov State Forecasting Based on Large-Scale Deep Neural Network Constraints. Eng. Proc. 2023, 39, 28. https://doi.org/10.3390/engproc2023039028
Molina C, Martinez J, Giraldo E. Dynamic Tikhonov State Forecasting Based on Large-Scale Deep Neural Network Constraints. Engineering Proceedings. 2023; 39(1):28. https://doi.org/10.3390/engproc2023039028
Chicago/Turabian StyleMolina, Cristhian, Juan Martinez, and Eduardo Giraldo. 2023. "Dynamic Tikhonov State Forecasting Based on Large-Scale Deep Neural Network Constraints" Engineering Proceedings 39, no. 1: 28. https://doi.org/10.3390/engproc2023039028
APA StyleMolina, C., Martinez, J., & Giraldo, E. (2023). Dynamic Tikhonov State Forecasting Based on Large-Scale Deep Neural Network Constraints. Engineering Proceedings, 39(1), 28. https://doi.org/10.3390/engproc2023039028






