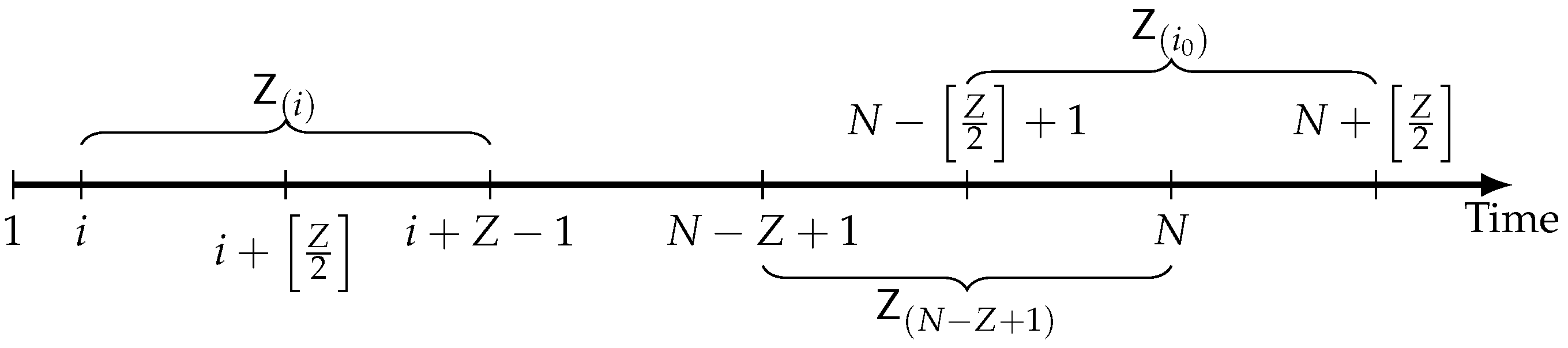Forecasting of Signals by Forecasting Linear Recurrence Relations ^†

Abstract

The forecasting of a signal that locally satisfies linear recurrence relations (LRRs) with slowly changing coefficients is considered. A method that estimates the local LRRs using the subspace-based method, predicts their coefficients and constructs a forecast using the LRR with the predicted coefficients is proposed. This method is implemented for time series that have the form of a noisy sum of sine waves with modulated frequencies. Linear and sinusoidal frequency modulations are considered. The application of the algorithm is demonstrated with numerical examples.

1. Introduction

Let us consider the problem of forecasting time series using singular spectrum analysis (SSA) [1,2,3,4,5,6]. The theory of SSA is quite well-developed; there are many papers with applications of SSA to real-life time series (see, for example, [6] and [7] (Section 1.7) with short reviews). SSA does not require a time-series model to construct the decomposition into interpretable components such as the trend, periodicities, and noise. However, for prediction in SSA, it is assumed that the signal (the deterministic component of the time series) ${\mathsf{S}}_N=(s_1,\dots ,s_N)$ satisfies some model, in particular, a linear recurrence relation (LRR) with constant coefficients (maybe, approximately):

$$s_{i+d}=\sum _{k=1}^d{a}_k{s}_{i+d-k}\mathrm{for}i=1,\dots ,N-d.$$

(1)

This assumption is valid for signals in the form of a sum of products of polynomial, exponential, and sinusoidal time series, in particular, a sum of exponentially modulated periodic components. SSA also works for the case of trend extraction and the general case of amplitude-modulated harmonics, where the model is satisfied approximately. However, SSA is not applicable if the signal locally satisfies a changing LRR. An example of such a signal is sinusoidal frequency-modulated time series. This paper aims to construct a method for the prediction of time series locally governed by changing LRRs, staying within the framework of SSA.

Let us consider the model of time series in the form of a noisy signal, where the signal is locally governed by LRRs with slowly time-varying coefficients. A local version of SSA has already been considered earlier for signal estimation [8]. However, it results in different approximations of the segments of the time series and the prediction can be performed based on the last segment only. In this paper, a local modification of the recurrent SSA prediction, based on the construction of a prediction of the coefficients of the local LRRs, is proposed. This modification was applied to time series in which the signal is a sum of sinusoids with time-varying frequencies having non-intersecting frequency ranges, where the instantaneous frequency of each summand is slowly varying.

2. Basic Notions

2.1. Linear Recurrence Relations

Let us introduce several definitions. By time series of length N we mean a sequence of real numbers ${\mathsf{X}}_N=(x_1,\dots ,x_N)\in {\mathbb{R}}^N$. Consider a time series in the form of the sum of a signal and noise ${\mathsf{X}}_N={\mathsf{S}}_N+{\mathsf{R}}_N$ and state the problem of signal forecasting.

A time series ${\mathsf{S}}_N$ satisfies a linear recurrence relation (LRR) of order d if there exists a sequence ${\left\{a_i\right\}}_{i=1}^d$ such that $a_d\ne 0$ and (1) takes place.

A time series governed by an LRR satisfies a set of LRRs, one of which has minimal order; we will call it minimal LRR. Among the set of the governing LRRs, there is the so-called min-norm LRR with the minimum norm of coefficients, which suppresses noise in the best way [5] and is used for the recurrent SSA forecasting.

The characteristic polynomial of LRR (1) is defined as

$$P_d\left(\mu \right)={\mu }^d-\sum _{k=1}^d{a}_k{\mu }^{d-k}.$$

The roots of the characteristic polynomial of the minimal LRR are called signal roots. The characteristic polynomial corresponding to an LRR governing the signal includes the signal roots, among others.

Remark 1.

Since $P_m\left(\mu \right)={\displaystyle \prod _{k=1}^m}(\mu -{\mu }_k)={\mu }^m-{\displaystyle \sum _{k=1}^m}{a}_k{\mu }^{m-k}$, the roots of the characteristic polynomial provides the LRR coefficients, and vice versa.

The following result [9] together with Remark 1 shows how to find the roots of the governing minimal LRR $s_{i+r}={\displaystyle \sum _{k=1}^r}{a}_k{s}_{i+r-k}$ using the common term of the time series ${\mathsf{S}}_N$. Let ${\mu }_1,\dots ,{\mu }_p$ be the roots of the LRR characteristic polynomial with multiplicities $k_1,\dots ,k_p$. The time series ${\mathsf{S}}_N$ satisfies the LRR if and only if $s_n={\displaystyle \sum _{m=1}^p}\left({\displaystyle \sum _{j=0}^{k_m-1}}{c}_{mj}{n}^j\right){\mu }_m^n$, where $c_{mj}\in \mathbb{C}$ depends on $s_1,\dots ,s_r$.

Example 1.

Consider the time series ${\mathsf{S}}_N=(s_1,\dots ,s_N)$ with $s_n=A\cos (2\pi \omega n+\varphi )$, $\omega \in \left(0,\frac{1}{2}\right)$. Since $A\cos (2\pi \omega n+\varphi )=A{e}^{-\mathrm{i}\varphi }{e}^{-\mathrm{i}·2\pi \omega n}/2+A{e}^{\mathrm{i}\varphi }{e}^{\mathrm{i}·2\pi \omega n}/2$, we have ${\mu }_1=e^{-\mathrm{i}·2\pi \omega }$, ${\mu }_2=e^{\mathrm{i}·2\pi \omega }$. Therefore, the characteristic polynomial is $P_r\left(\mu \right)=(\mu -{\mu }_1)(\mu -{\mu }_2)=(\mu -e^{-\mathrm{i}·2\pi \omega n})(\mu -e^{\mathrm{i}·2\pi \omega n})={\mu }^2-2\mu \cos 2\pi \omega +1$. Thus, $a_1=2\cos 2\pi \omega$, $a_2=-1$ and $s_{i+2}=2s_{i+1}\cos 2\pi \omega -s_i$.

Remark 2.

The method for constructing the min-norm LRR of a given order with the given signal roots is described in [10]. This method will be used in the algorithm proposed in Section 3.2.

2.2. Harmonic Signal with Time-Varying Frequency: Instantaneous Frequency

In this paper, the basic form of signals will be the discrete-time version of

$$s\left(t\right)={\displaystyle \sum _{i=1}^p}\cos \left(2\pi {\omega }_i\left(t\right)+{\varphi }_i\right),$$

(2)

where ${\omega }_i\left(t\right)$, $i=1,\dots ,p$, are slowly changing functions. Note that if ${\omega }_i\left(t\right)$ are linear functions, the signal satisfies an LRR; see [4] (Section 2.2) and Remark 1.

Let $s\left(t\right)=\cos \left(2\pi \psi \left(t\right)+\varphi \right)$. The instantaneous frequency of the signal $s\left(t\right)$ is defined as ${\omega }_{\mathrm{ins}}\left(t\right)={\psi }^{\prime }\left(t\right)$. The instantaneous period is the function $T_{\mathrm{ins}}\left(t\right)=\frac{1}{{\omega }_{\mathrm{ins}}\left(t\right)}$. If ${\omega }_{\mathrm{ins}}\left(a\right)=0$ for some a, we put $T_{\mathrm{ins}}\left(a\right)=+\infty$. The frequency range of the signal ${\mathsf{S}}_N$ is the range ${\omega }_{\mathrm{ins}}\left([1,N]\right)$, that is, the image of $[1,N]$.

Example 2.

For the signal $s\left(t\right)=\cos \left(2\pi {\left(\frac{t}{100}\right)}^2\right)$, the instantaneous frequency ${\omega }_{\mathrm{ins}}\left(t\right)=\frac{t}{5000}$ is a linear function; the frequency range equals ${\omega }_{\mathrm{ins}}\left([1,N]\right)=\left[\frac{1}{5000},\frac{N}{5000}\right]$. For the signal $s\left(t\right)=\cos \left(\frac{2\pi }{20}\left(t+5sin\frac{2\pi t}{100}\right)\right)$, the instantaneous frequency equals ${\omega }_{\mathrm{ins}}\left(t\right)=\frac{1}{20}\left(1+\frac{5·2\pi }{100}\cos \frac{2\pi t}{100}\right)$ and is a periodic function with period equal to $T=100$; the frequency range is

$${\omega }_{\mathrm{ins}}\left([1,N]\right)\subset \left[\frac{1}{20}\left(1-\frac{\pi }{10}\right),\frac{1}{20}\left(1+\frac{\pi }{10}\right)\right].$$

We assume that on short segments of time, the signals considered in Example 2 are well-enough approximated by a sinusoid with a frequency equal to the instantaneous frequency in the middle of the segment. This assumption will be used for the construction of the signal-forecasting algorithm.

2.3. SSA, Signal Subspace and Recurrent SSA Forecasting

In the version for signal extraction, SSA has two parameters, the window length L, $1<L<N$, where N is the time-series length, and the number of elementary components r. At the first step of SSA, the trajectory matrix of size $L\times K$, where $K=N-L+1$, is constructed and then decomposed into elementary components using the SVD. The leading r SVD components are used for the estimation of the signal and the signal subspace basis, which is used for constructing the forecasting LRR. Here is the scheme of the method given in [6]:

$$\begin{array}{c}\hfill \mathsf{X}{\displaystyle \underset{\boxed{L}}{\overset{\mathcal{T}}{\to }}}\mathbf{X}=\left(\begin{array}{cccc}{x}_1& x_2& \dots & x_K\\ x_2& x_3& \dots & x_{K+1}\\ ⋮& ⋮& \ddots & ⋮\\ x_L& x_{L+1}& \dots & x_N\end{array}\right){\displaystyle \underset{\boxed{r}}{\overset{\mathrm{SVD}:(\sqrt{{\lambda }_m},U_m,V_m),{\Pi }_r}{\to }}}\end{array}$$

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{L}}_r=span(U_1,\dots ,U_r)\hfill \\ \mathrm{is} \mathrm{the} \mathrm{signal} \mathrm{space};\hfill \\ {\Pi }_r\mathrm{is} \mathrm{the} \mathrm{projector} \mathrm{on}{\mathcal{L}}_r;\hfill \\ \widehat{\mathbf{S}}={\displaystyle \sum _{m=1}^r}{U}_m{\left({\mathbf{X}}^{\mathrm{T}}{U}_m\right)}^{\mathrm{T}}={\Pi }_r\mathbf{X}.\hfill \end{array}\right.\stackrel{{\Pi }_{\mathcal{H}}}{\to }\tilde{\mathbf{S}}=\left(\begin{array}{cccc}{\tilde{s}}_1& {\tilde{s}}_2& \dots & {\tilde{s}}_K\\ {\tilde{s}}_2& {\tilde{s}}_3& \dots & {\tilde{s}}_{K+1}\\ ⋮& ⋮& \ddots & ⋮\\ {\tilde{s}}_L& {\tilde{s}}_{L+1}& \dots & {\tilde{s}}_N\end{array}\right)\stackrel{{\mathcal{T}}^{-1}}{\to }\tilde{\mathsf{S}}.\end{array}$$

Thus, a concise form of the SSA algorithm for signal extraction is

$$\tilde{\mathsf{S}}={\mathcal{T}}^{-1}\circ {\Pi }_{\mathcal{H}}\circ {\Pi }_r\circ \mathcal{T}\left(\mathsf{X}\right),$$

where ${\Pi }_{\mathcal{H}}$ is the projector to the set of Hankel matrices, that is, the set of trajectory matrices.

The L-rank of a time series is the rank of its trajectory matrix $\mathcal{T}\left(\mathsf{X}\right)$, or, equivalently, the dimension of the column space of $\mathcal{T}\left(\mathsf{X}\right)$. For infinite time series and $L>r$, the rank is equal to the order of the minimal LRR governing the time series. For example, the rank of the signal ${\mathsf{S}}_{\infty }=(s_1,s_2,\dots )$ with the common term $s_n=A\cos (2\pi \omega n+\varphi )$ and $\omega \in \left(0,\frac{1}{2}\right)$ equals two.

The construction of the forecasting min-norm LRR of order $L-1$ based on the SSA decomposition follows the formula for the LRR coefficients $\mathcal{R}$ [4] (Equation (2.1)):

$$\mathcal{R}=\frac{1}{1-{\nu }^2}{\displaystyle \sum _{i=1}^r}{\pi }_i\underline{U_i}=:(a_{L-1},\dots ,a_1),$$

(3)

where $\underline{U_i}\in {\mathbb{R}}^{L-1}$ is the vector $U_i$ without the last coordinate, which is denoted by ${\pi }_i$. The forecast is constructed as ${\tilde{s}}_{N+1}={\sum }_{i=1}^{L-1}{a}_i{\tilde{s}}_{N+1-i}$.

In addition to forecasting, the SSA decomposition allows one to estimate the signal roots. Let us describe the ESPRIT (see [7] (Algorithm 3.3) and [11]) for signal-root estimation. We define $\mathbf{U}:=[U_1:\dots :U_r]$, $\overline{\mathbf{U}}$ the matrix $\mathbf{U}$ without the first row and $\underline{\mathbf{U}}$ the matrix $\mathbf{U}$ without the last row. The ESPRIT estimates of the signal roots ${\left\{{\mu }_k\right\}}_{k=1}^r$ are the eigenvalues of a matrix that is an approximate solution of the equation $\underline{\mathbf{U}}\mathbf{D}=\overline{\mathbf{U}}$; e.g., $\mathbf{D}={\left({\underline{\mathbf{U}}}^{\mathrm{T}}\underline{\mathbf{U}}\right)}^{-1}{\underline{\mathbf{U}}}^{\mathrm{T}}\overline{\mathbf{U}}$ for the LS-ESPRIT version.

3. Signal Forecasting by Forecasting of Local LRRs

3.1. General Model of Signals

Let us describe a general model of time series, for which the developed approach to forecasting will be applied. Consider the signal ${\mathsf{S}}_N$ and take some natural Z, $1<Z<N$. For a time series $\mathsf{Y}$, we denote ${\mathsf{Y}}_{A,B}$ the series $(y_A,\dots ,y_B)$.

The signal model is

$$s_n={\displaystyle \sum _{j=1}^p}{\rho }_j^n\left(n\right)\cos (2\pi {\psi }_j\left(n\right)+{\phi }_j),$$

(4)

where we assume that

1.

For the time series $\mathsf{S}$, on its sequential segments ${\mathsf{S}}_{i,i+Z-1}$ of length Z,

$i=1,\dots ,N-Z+1$, every summand in (4) is well-approximated by a series in the form $s_n^{\mathrm{approx}}={\rho }_j^n\left(n_0\right)\cos (2\pi {\omega }_{j,0}·n+\varphi )$, where ${\omega }_{j,0}={\psi }_j^{\prime }\left(n_0\right)$ and $n_0=n_0\left(i\right)$ is the middle point of the segment.

2.

The series ${\rho }_j\left(n\right)$ and ${\psi }_j^{\prime }\left(n\right)$ behave regularly in n, $0<{\psi }_j^{\prime }\left(n\right)<0.5$ and there exist methods that can forecast such kinds of series.

To construct a forecast $s_{N+1}$ one needs to find the instantaneous frequencies at the point $N+1$.

3.2. Algorithm LocLRR SSA Forecast

Hereinafter, we will consider the model ${\mathsf{X}}_N={\mathsf{S}}_N+{\mathsf{R}}_N$, where ${\mathsf{S}}_N=(s_1,\dots ,s_N)$ satisfies the conditions described above and ${\mathsf{R}}_N$ is white Gaussian noise with zero mean and standard deviation $\sigma$. Let ${\mathsf{Z}}_{\left(i\right)}={\mathsf{X}}_{i,i+Z-1}$, $i=1,\dots ,W$, where $W=N-Z+1$. The estimates of instantaneous roots, frequencies, moduli and LRR coefficients will be enumerated according to the middle of the local segment. In particular, denote ${\left\{a_k^{\left(i\right)}\right\}}_{k=1}^r$ the coefficients of the minimal LRR that approximates the local segment of the series $S_{i-\left[Z/2\right],i+\left[Z/2\right]-1}$ with the center in $s_i$.

The local segment of length Z has the structure depicted in Figure 1, where the middle of ${\mathsf{Z}}_{\left(i_0\right)}$ is $N+1$.

Figure 1. Scheme of moving segments.

3.2.1. Scheme

In the scheme below, we consider $j=1,\dots ,p^{\prime }$, where $p^{\prime }$ is the number of signal roots with nonnegative imaginary parts (note that signal roots with negative imaginary parts are conjugate to signal roots with positive imaginary parts):

$$\begin{array}{cccccc}{\mathsf{X}}_N& & {\left\{{\rho }_j^{(i+\left[Z/2\right])}\right\}}_{i=1}^W& \stackrel{\mathrm{FOR}\mathrm{MODs}}{\to }& {\left\{{\tilde{\rho }}_j^{(N+l)}\right\}}_{l=1}^M& \\ \downarrow Z& & \uparrow & & \downarrow & \\ {\left\{{\mathsf{Z}}_{\left(i\right)}\right\}}_{i=1}^W& {\displaystyle \underset{L,r}{\overset{ESPRIT}{\to }}}& {\left\{{\mu }_j^{(i+\left[Z/2\right])}\right\}}_{i=1}^W& & {\left\{{\tilde{\mu }}_j^{(N+l)}\right\}}_{l=1}^M& \to {\left\{{\tilde{\mathcal{R}}}_{N+l}\right\}}_{l=1}^M.\\ & & \downarrow & & \uparrow & \\ & & {\left\{{\omega }_j^{(i+\left[Z/2\right])}\right\}}_{i=1}^W& \stackrel{\mathrm{FOR}\mathrm{ARGs}}{\to }& {\left\{{\tilde{\omega }}_j^{(N+l)}\right\}}_{l=1}^M& \end{array}$$

Here ${\left\{{\tilde{\mathcal{R}}}_{N+l}\right\}}_{l=1}^M$, where ${\tilde{\mathcal{R}}}_k=({\tilde{a}}_r,\dots ,{\tilde{a}}_1)$ is the sequence of coefficients of the forecasting minimal LRRs. If the required length m of the forecasting LRRs is larger than r, then we lengthen each ${\tilde{\mathcal{R}}}_{N+l}$, $l=1,\dots ,M$, to ${\tilde{\mathcal{R}}}_{N+l}^{\left(m\right)}$ of the min-norm LRR of order m; see Remark 2.

The result is a sequence of coefficients of the forecasting min-norm LRRs ${\left\{{\tilde{\mathcal{R}}}_{N+l}^{\left(m\right)}\right\}}_{l=1}^M$ of order m. To obtain the results, the series of moduli and frequencies should be forecasted using some algorithms FOR MODs and FOR ARGs for each j.

After the sequence of coefficients is constructed, the forecasting values ${\tilde{\mathsf{S}}}_{N+1,N+M}=(y_{N+1},\dots ,y_{N+M})$ are taken from the time series

$$y_n=\left\{\begin{array}{c}{\tilde{s}}_n,n=1,\dots ,N,\hfill \\ {\displaystyle \sum _{k=1}^m}{\tilde{a}}_k^{\left(n\right)}{y}_{n-k},n=N+1,\dots ,N+M,\hfill \end{array}\right.$$

where ${\tilde{s}}_n$, $n=1,\dots ,N,$ is the signal estimate obtained using SSA.

3.2.2. Algorithm in Detail

Let us formally describe the algorithm for forecasting the minimal LRRs (Algorithm 1).

Algorithm 1: LocLRR SSA Forecast

Input: time series ${\mathsf{X}}_N=(x_1,\dots ,x_N)$, forecast length M, local segment length Z, window length L, number r of leading eigentriples of the trajectory matrices of the local segments that are used to find the estimates of the signal roots, length m of the forecasting LRRs, algorithm for forecasting the root moduli $\mathrm{FOR}\mathrm{MODs}$, algorithm for forecasting the instantaneous frequencies $\mathrm{FOR}\mathrm{ARGs}$. Steps: For each segment ${\mathsf{Z}}_{\left(i\right)}$, $i=1,\dots ,W$, where $W=N-Z+1$, estimate the signal roots ${\left\{{\mu }_j^{(i+\left[Z/2\right])}\right\}}_{j=1}^r$ of the approximating series using ESPRIT with window length L and signal rank r. Suppose that the estimates of the roots form complex-conjugate pairs. Choose the roots with positive argument ${\left\{{\mu }_j^{(i+\left[Z/2\right])}\right\}}_{j=1}^p$, $i=1,\dots ,W$, $p=\frac{r}{2}$. Arrange the first set of roots ${\left\{{\mu }_j^{(1+\left[Z/2\right])}\right\}}_{j=1}^p$ in descending argument order. Order the sets of roots ${\left\{{\mu }_j^{(i+\left[Z/2\right])}\right\}}_{j=1}^p$, $i=2,\dots ,W$, so that the sum $${\displaystyle \sum _{j=1}^p}\left|{\mu }_j^{(i+\left[Z/2\right])}-{\mu }_j^{(i+\left[Z/2\right]-1)}\right|$$ is minimal among all possible permutations of ${\left\{{\mu }_j^{(i+\left[Z/2\right])}\right\}}_{j=1}^p$. For each $i=1,\dots ,W$ and $j=1,\dots ,p$, calculate the moduli ${\rho }_j^{(i+\left[Z/2\right])}=\left|{\mu }_j^{(i+\left[Z/2\right])}\right|$ and the frequencies ${\omega }_j^{(i+\left[Z/2\right])}=\frac{Arg{\mu }_j^{(i+\left[Z/2\right])}}{2\pi }$. For $j=1,\dots ,p$, set the series $P_{\left(j\right)}=\left({\rho }_j^{(1+\left[Z/2\right])},\dots ,{\rho }_j^{(N-\left[Z/2\right]+1)}\right)$ and ${\mathsf{\Omega }}_{\left(j\right)}=\left({\omega }_j^{(1+\left[Z/2\right])},\dots ,{\omega }_j^{(N-\left[Z/2\right]+1)}\right)$. Using the algorithms $\mathrm{FOR}\mathrm{MODs}$ and $\mathrm{FOR}\mathrm{ARGs}$, for each $j=1,\dots ,p$, construct the forecast $\left({\tilde{\rho }}_j^{(N+1)},\dots ,{\tilde{\rho }}_j^{(N+M)}\right)$ of the series $P_{\left(j\right)}$ and the forecast $\left({\tilde{\omega }}_j^{(N+1)},\dots ,{\tilde{\omega }}_j^{(N+M)}\right)$ of ${\mathsf{\Omega }}_{\left(j\right)}$, respectively. Using the obtained forecasts of frequencies and moduli, calculate the roots ${\tilde{\mu }}_j^{\left(n\right)}={\tilde{\rho }}_j^{\left(n\right)}exp\left(\mathrm{i}2\pi {\tilde{\omega }}_j^{\left(n\right)}\right)$, $n=N+1,\dots ,N+M$, $j=1,\dots ,p$, supplement them by their complex conjugates and then, using the relation between characteristic polynomials and LRRs (see Remark 1), find the sequence ${\left\{{\tilde{\mathcal{R}}}_{N+j}\right\}}_{j=1}^M$ of the LRR coefficients, ${\tilde{\mathcal{R}}}_{N+j}=\left({\tilde{a}}_r^{(N+j)},\dots ,{\tilde{a}}_1^{(N+j)}\right)$. Output: The sequence ${\left\{{\tilde{\mathcal{R}}}_{N+l}\right\}}_{l=1}^M$ of coefficients of minimal LRRs of order r approximately governing the future signal segments ${\mathsf{S}}_{l+N-\left[Z/2\right]-1,l+N+\left[Z/2\right]}$.

Remark 3.

If real-valued roots are obtained on some segments of ${\mathsf{Z}}_{\left(i\right)}$, $i=1,\dots ,W$, we replace the values of the roots with missing values. That is, for $i=1,\dots ,W$ and $j=1,\dots ,r$ such that ${\mu }_j^{\left(i\right)}\in \mathbb{R}$ we put ${\mu }_j^{\left(i\right)}:=NA\left(\mathrm{not}\mathrm{available}\right)$. Possible gaps in the series of frequency estimates can be filled in; e.g., one can fill them with the iterative gap-filling method [12]; see also the description of the igapfill algorithm in [7] (Algorithm 3.7).

An appropriate choice of the algorithms $\mathrm{FOR}\mathrm{MODs}$ and $\mathrm{FOR}\mathrm{ARGs}$ depends on the form of the frequency modulation.

Finally, each LRR of ${\left\{{\tilde{\mathcal{R}}}_{N+j}\right\}}_{j=1}^M$ is enlarged to a min-norm LRR of length m with coefficients ${\left\{{\tilde{\mathcal{R}}}_{N+l}^{\left(m\right)}\right\}}_{l=1}^M$ (see Remark 2) and this enlarged LRR is used for the prediction of $s_{N+l}$.

4. Examples

4.1. Description

In this section, we demonstrate the forecasting using the LocLRR SSA Forecast algorithm. The following types of time series were considered.

4.1.1. Sinusoid with Linearly Modulated Frequency

The signal has the form

$$s\left(t\right)=\cos \left(2\pi {\left(at\right)}^2\right),a\ne 0.$$

The instantaneous frequency is ${\omega }_{\mathrm{ins}}\left(t\right)=2a^{2}t$; the frequency range is ${\omega }_{\mathrm{ins}}\left([1,N]\right)=\left[2a^2,2a^{2}N\right]$. We will consider such values of the parameter a and series length N at which the frequency range ${\omega }_{\mathrm{ins}}\left([1,N]\right)\subset (0,0.5)$. Since the instantaneous frequency is a linear function, we will take the linear-regression-prediction algorithm as $\mathrm{FOR}\mathrm{ARGs}$.

4.1.2. Sinusoid with Sinusoidal Frequency

The signal is

$$s\left(t\right)=\cos \left(2\pi {\omega }_{\mathrm{ext}}\left(t+bsin2\pi {\omega }_{\mathrm{int}}t\right)\right),b>0,$$

${\omega }_{\mathrm{ext}},{\omega }_{\mathrm{int}}\in (0,0.5)$, where ${\omega }_{\mathrm{int}}$ is much smaller than ${\omega }_{\mathrm{ext}}$. The instantaneous frequency equals ${\omega }_{\mathrm{ins}}\left(t\right)={\omega }_{\mathrm{ext}}(1+2\pi {\omega }_{\mathrm{int}}b\cos 2\pi {\omega }_{\mathrm{int}}t)$; the frequency range is ${\omega }_{\mathrm{ins}}\left([1,N]\right)=\left[{\omega }_{\mathrm{ext}}(1-2\pi {\omega }_{\mathrm{int}}b),{\omega }_{\mathrm{ext}}(1+2\pi {\omega }_{\mathrm{int}}b)\right]$. We will consider values of signal parameters and series lengths such that ${\omega }_{\mathrm{ins}}\left([1,N]\right)\subset (0,0.5)$. The rank of the time series of the series ${\mathsf{\Omega }}_N$ of instantaneous frequencies with terms ${\omega }_n={\omega }_{\mathrm{ins}}\left(n\right)$, $n=1,\dots ,N$, is equal to 3. Therefore, we take the recurrent SSA forecasting algorithm with $r=3$ as $\mathrm{FOR}\mathrm{ARGs}$; the window length L is chosen to be half of the length of the frequency-estimation series following the general recommendations.

Since we do not consider time-varying amplitude modulation in the examples, we take the forecast of moduli series using the average value over local intervals as algorithm $\mathrm{FOR}\mathrm{MODs}$.

4.1.3. Sum of Sinusoids

The signal is

$$s\left(t\right)={\displaystyle \sum _{j=1}^{p_1}}\cos \left(2\pi {\left(a_{j}t\right)}^2\right)+{\displaystyle \sum _{k=1}^{p_2}}\cos \left(2\pi {\omega }_k^{\mathrm{ext}}\left(t+b_{k}sin2\pi {\omega }_k^{\mathrm{int}}t\right)\right),$$

(5)

$a_j\ne 0$, $j=1,\dots ,p_1$, ${\omega }_k^{\mathrm{ext}},{\omega }_k^{\mathrm{int}}\in (0,0.5)$, $b_k>0$, $k=1,\dots ,p_2$. We will consider the signal parameters and the time-series length N such that the frequency ranges of the summands are not mutually intersected and the frequency range of each summand belongs to the interval $(0,0.5)$.

The frequencies corresponding to the signal summands of $s\left(t\right)$ will be forecasted either with linear regression or with SSA, based on the type of obtained estimates of the instantaneous frequencies on the local segments. The moduli will be predicted using the average of the estimates over the local segments.

In numerical examples, we will consider the signal parameters such that the instantaneous frequencies are slow-varying functions. Since the examples under consideration satisfy the general time-series model (Section 3.1), the LocLRR SSA-forecast algorithm can be used for forecasting.

In real-life problems, the value of the optimal LRR order m can be chosen based on the training data. In the model examples, the value of the optimal LRR order m will be chosen by trying all possible values of m in the range from r to Z and comparing the mean squared errors (MSE) of the predictions.

The following approach was used for choosing the length Z of local segments. We take such a value of the parameter Z that most of the local segments ${\mathsf{Z}}_{\left(i\right)}$, $i=1,\dots ,W$, contain at least 2–3 instantaneous periods of each summand of the signal satisfying model (5). For small Z, we obtain estimates of the instantaneous frequency with large variability, whereas for large Z, we have a considerable bias. The necessary condition for appropriate values of Z is that there are no (or a few) segments providing real-valued roots.

4.2. Numerical Experiments

Consider the following numerical examples:

• Sinusoid with linearly modulated frequency,

  $$s_n=\cos \left(2\pi {\left(\frac{n}{100}\right)}^2\right)$$
  (denoted by $\cos \left({\mathsf{n}}^{\mathsf{2}}\right)$);
• Sinusoid with sinusoidal frequency modulation,

  $$s_n=\cos \left(\frac{2\pi }{20}\left(n+5sin\frac{2\pi n}{100}\right)\right)$$
  (denoted by $\cos sin\left(\mathsf{n}\right)$);
• Sum of sinusoids with linear and sinusoidal frequency modulations,

  $$s_n=\cos \left(2\pi {\left(\frac{n}{100}\right)}^2\right)+\cos \left(\frac{2\pi }{10}\left(n+sin\frac{2\pi n}{100}\right)\right)$$

  (6)
  (denoted by $\cos ({\mathsf{n}}^{\mathsf{2}})+\cos sin\left(\mathsf{n}\right)$);
• Sum of two sinusoids with sinusoidal frequency modulation,

  $$s_n=\cos \left(\frac{2\pi }{20}\left(n+sin\frac{2\pi n}{100}\right)\right)+\cos \left(\frac{2\pi }{10}\left(n+2sin\frac{2\pi n}{140}\right)\right)$$
  (denoted by $\cos sin\left(\mathsf{n}\right)+\cos sin\left(\mathsf{n}\right)$).

We compare the proposed LocLRR SSA-forecast algorithm (denoted by “alg”) with two simple methods:

• Forecasting by constant, which forecasts by zero, since we consider time series with zero average (denoted by ‘by 0’).
• Forecasting using the last local segment, which is performed with the min-norm LRR computed using the roots of the last local segment ${\mathsf{Z}}_{(N-Z+1)}=(x_{N-Z+1},\dots ,x_N)$ (denoted by ‘last’).

Let us consider accuracies of $M=30$ step ahead forecasts for time series of length $N=300$. For each example, the prediction is performed for the pure signal and the noisy signal, where the noise is white Gaussian with standard deviation $\sigma =0.25$. In the noisy case, a sample of size $P=100$ is used for the estimation of accuracy.

Let ${\left\{{\mathsf{X}}_N^{\left(i\right)}\right\}}_{i=1}^P$ be the time-series sample. The prediction error is estimated as $RMSE=\sqrt{\frac{1}{P}{\displaystyle \sum _{i=1}^P}MSE({\tilde{\mathsf{S}}}_{N+1,N+M}^{\left(i\right)},{\mathsf{S}}_{N+1,N+M})}$.

The results are shown in Table 1, where the best results are highlighted in bold. They confirm the advantage of the proposed method over the simple methods under consideration.

Table 1. RMSE of forecasts; ‘alg’ is the proposed algorithm; m is the optimal length of the forecasting LRRs.

Signal ${\mathsf{S}}_{\mathit{N}}$	$\mathit{\sigma }$	by 0	Last		Alg
			RMSE	m	RMSE	m
$\cos \left({\mathsf{n}}^{\mathsf{2}}\right)$	0	0.689	0.717	2	0.014	3
	0.25	0.733	0.754	5	0.135	11
$\cos sin\left(\mathsf{n}\right)$	0	0.698	0.309	2	0.097	2
	0.25	0.741	0.438	5	0.232	6
$\cos \left({\mathsf{n}}^{\mathsf{2}}\right)+\cos sin\left(\mathsf{n}\right)$	0	1.060	0.880	6	0.184	4
	0.25	1.089	0.958	10	0.295	12
$\cos sin\left(\mathsf{n}\right)+\cos sin\left(\mathsf{n}\right)$	0	0.873	0.587	4	0.191	5
	0.25	0.908	0.656	28	0.291	15

4.3. Detailed Example

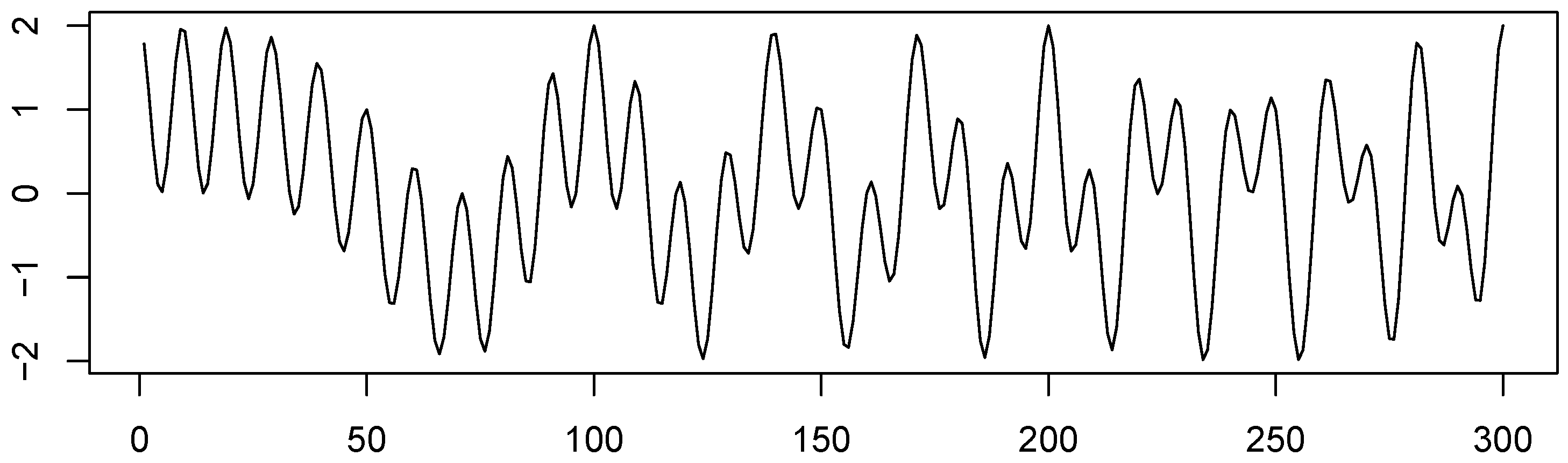
To demonstrate the approach more clearly, let us consider the example (6) without noise; see Figure 2. Take $Z=61$, $L=30$, $r=4$.

Figure 2. Initial signal $s_n=\cos \left(2\pi {\left(\frac{n}{100}\right)}^2\right)+\cos \left(\frac{2\pi }{10}\left(n+sin\frac{2\pi n}{100}\right)\right)$.

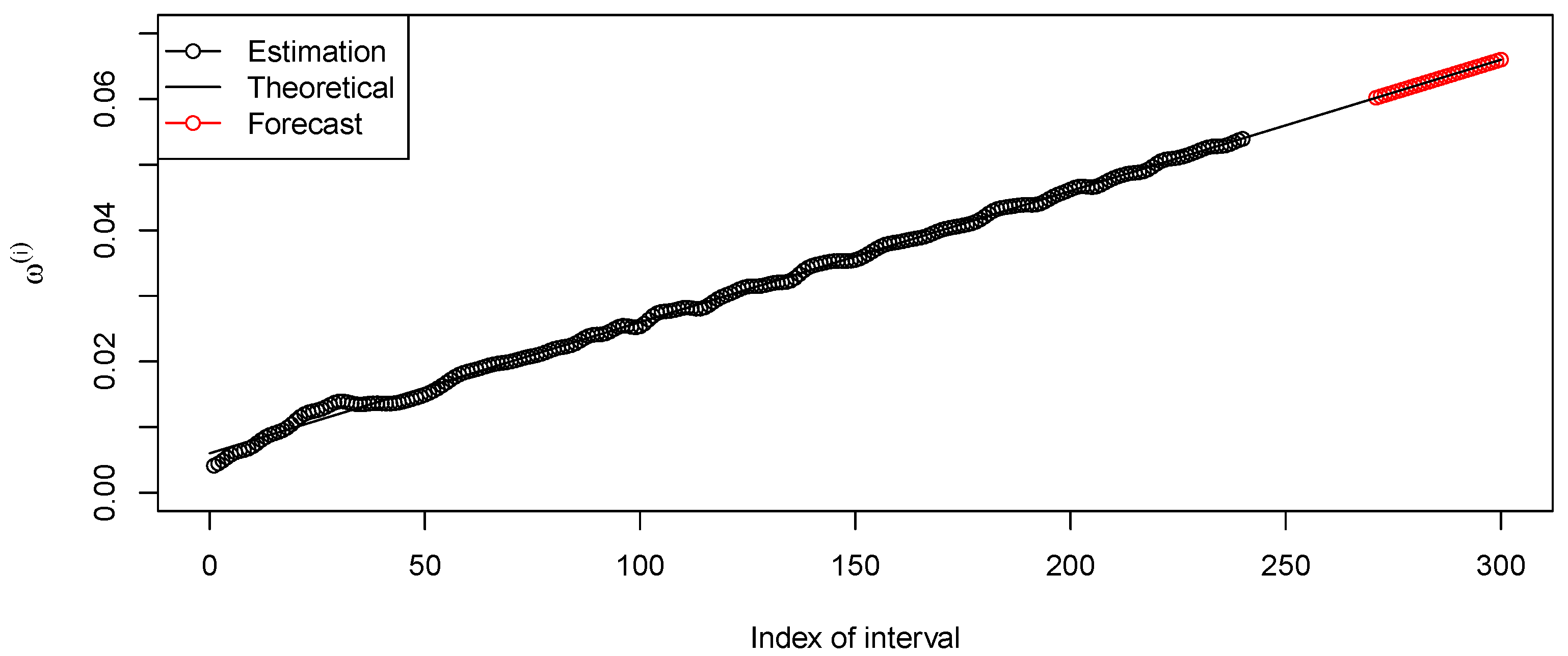
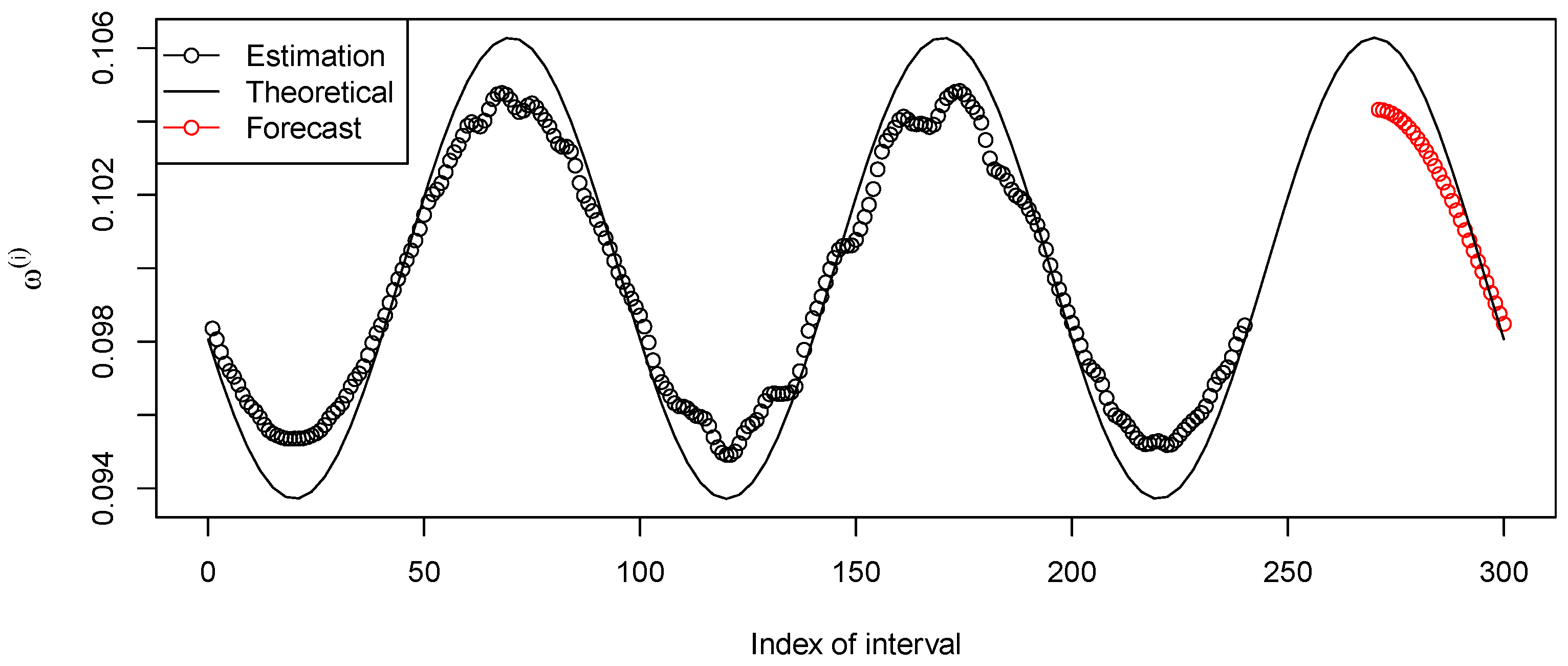
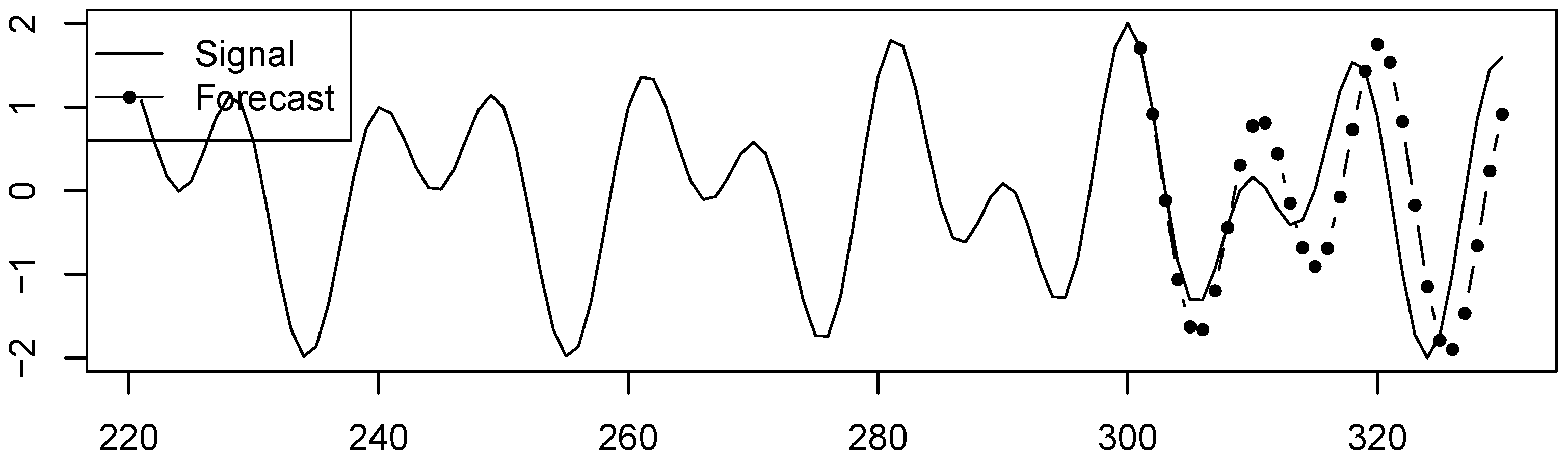
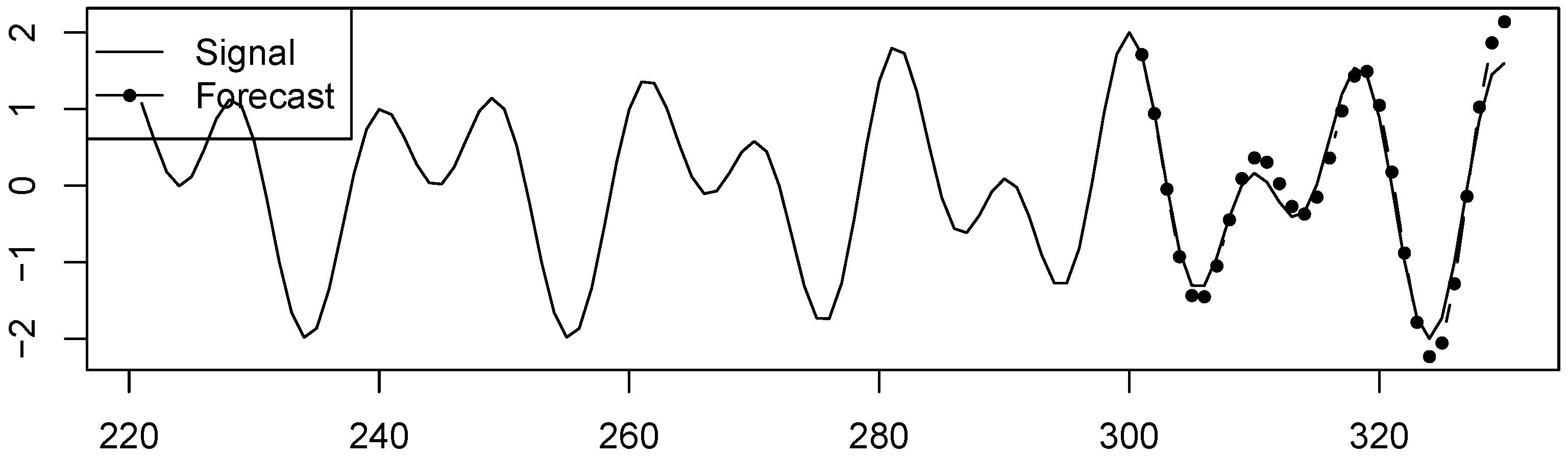
The results of forecasting the signal root corresponding to the first summand are shown in Figure 3, and the results of forecasting the signal root corresponding to the second summand can be seen in Figure 4. The frequency ranges of modulations in the summands are approximately $[0,0.06]$ and $[0.094,0.106]$, respectively. The forecasts are depicted in Figure 5 (forecasting with the last segment) and Figure 6 (forecasting with the proposed algorithm). Since there is no noise, the optimal LRR length m is small; here, $m=4$.

Figure 3. Forecasting the series of linear instantaneous frequencies for the summand $\cos \left(2\pi {\left(\frac{n}{100}\right)}^2\right)$.

Figure 4. Forecasting the series of sinusoidal instantaneous frequencies for the summand $\cos \left(\frac{2\pi }{10}\left(n+sin\frac{2\pi n}{100}\right)\right)$.

Figure 5. Forecasting using the last local segment, $RMSE=0.88$. A shift is clearly seen.

Figure 6. Forecasting using LocLRR SSA forecast, $RMSE=0.2$. There is no shift.

5. Conclusions

In this paper, we proposed a method for forecasting time series that extends the capabilities of SSA and allows one to predict time series in which the signal just locally satisfies LRRs. A regular behaviour of the coefficients of the governed LRRs was assumed. In [6] (page 9), it was stated for the considered type of time series that “[t]he problem is how to forecast the extracted signal, since its local estimates may have different structures on different time intervals. Indeed, by using local versions of SSA, we do not obtain a common nonlinear model but instead we have a set of local linear models”. In this paper, we proposed an answer to the problem of prediction of local structures of time series for some class of signals.

We constructed an algorithm for predicting local structures of time series that are the sum of frequency-modulated sinusoids and showed that the proposed forecasting method gives reasonable results for the cases of linear and sinusoidal frequency modulations.

Certainly, the considered comparison with a couple of simple methods is not enough; a more extensive comparison should be performed in the future. However, the results of this work show that the proposed approach based on the prediction of the coefficients of LRRs is promising.