Fault Detection of Multi-Rate Two Phase Reactor Condenser System with Recycle Using Multiple Probabilistic Principal Component Analysis ^†

Abstract

Fault detection in multi-rate process systems is a challenging task. Common techniques used for fault detection include threshold-based detectors, statistical detectors, and machine learning-based detectors. One such statistical detector technique is multiple probabilistic principal component analysis (MPPCA). MPPCA uses probabilistic PCA to detect fault signals from multiple sensors without down-sampling or up-sampling. This paper uses MPPCA to detect faults in a two-phase reactor–condenser system with recycle (TPRCR) with three measurement classes. These measurement data are used to build the MPPCA model using expectation maximization (EM). Based on this, T² and SPE statistics are generated for fault detection in TPRCR systems, and the MPPCA approach’s effectiveness for fault detection is satisfactory.

1. Introduction

Modern chemical industries focus on detecting and diagnosing faults as early as possible to increase production yield [1]. Effective fault-detection techniques available in the literature require the regular availability of measurements [1]. However, some variables in chemical processes are measured online, while other qualitative variables are measured offline. Measurement of these offline quality variables requires human involvement, which makes the system an irregularly sampled multi-rate system [2]. Fault-detection techniques for multi-rate systems include state space estimation techniques and data-based modelling methods. State space estimation techniques require accurate system models, which are difficult to model for complex chemical engineering systems. Compared to the above methods, another data-driven approach uses measurement data to model the system’s behaviour. These data-driven methods for multi-rate systems require down-sampling, up-sampling and re-sampling. While the down-sampling approaches will lose essential information during modelling, the up-sampling methods heavily rely on the correctness of the predictions [3]. In most chemical processes, the variation in sample rates is too significant, resulting in unmanageable complexity in the re-sampling models. The MPPCA method does not require down-sampling, up-sampling and re-sampling of multi-rate data. It uses multi-rate data to build an inferential model that can handle multiple measurement classes. The MPPCA method is an extension of probabilistic principal component analysis (PPCA) which uses the EM algorithm for parameter tuning.

In this study, the effectiveness of the MPPCA method in detecting various faults for the multi-rate nonlinear chemical process TPRCR is studied, and fault detection is carried out by using T² and SPE statistics.

The remainder of this paper is organised as follows. Section 2 gives details about the MPPCA method and model parameter estimation. Then, Section 3 details the TPRCR model. Section 4 implements a fault-detection technique on TPRCR. Finally, conclusions are made in the last section.

2. MPPCA Method

The MPPCA model combines several-rate data into a single model without down- or up-sampling. In our article, we have considered the MPPCA model with three different classes of measurements, and it is given by the following equations:

$$x_1={Ø}_{1}t+{\epsilon }_1$$

(1)

$$x_2={Ø}_{2}t+{\epsilon }_2$$

(2)

$$x_3={Ø}_{3}t+{\epsilon }_3$$

(3)

In Equations (1)–(3), x₁ ∈ R^K1×M1, x₂ ∈ R^K2×M2, and x₃ ∈ R^K3×M3 are three different rate measurements classes in which x₃ is the slowest and x₁ is the fastest measurement. ${Ø}_1$ ∈ R^M1×D, ${Ø}_2$ ∈ R^M2×D and ${Ø}_3$ ∈ R^M3×D are loading matrices with three different sampling rates. t ∈ R^D is a latent variable which extracts a restricted link between data with varied sampling rates and helps develop one single model. The latent variable is assumed to have a Gaussian distribution with a zero mean and unit variance. ε₁ ∈ R^M1, ε₂ ∈ R^M2 and ε₃ ∈ R^M3 are used to model the corresponding isotropic Gaussian noises.

The sequence of the measurements can be altered for easier notation and visualisation on the premise that all sample variables are independent. The whole observation (V) comprises three divisions of the observed data. The first sample contains all observations with dimensions M1 + M2 + M3 (V₃), the following sample variables have dimensions M1 + M2 (V₂), and the last one contains only M1 (V₁) variables. As a result, the entire observation set is expressed as a union of all three.

$$V=V_3\cup V_2\cup V_1$$

(4)

The EM technique is used to estimate model parameters for the MPPCA model. The method repeats the expectation step (E-step) and the maximisation step (M-step) until convergence. In the E-step, the current model parameters are utilised to estimate the posterior distributions of the latent variables. The model parameters are then adjusted in the M-step by maximising log likelihood. One reference contains a detailed explanation of the step of the EM algorithm for MPPCA training [4].

SPE statistics can be used to detect abnormal behaviour in measurements. There are three different classes of measurements, so three different SPE statistics are used to detect any anomaly in measurement.

$$SP{E}_1=x_1-{Ø}_{1}t$$

(5)

$$SP{E}_2=x_2-{Ø}_{2}t$$

(6)

$$SP{E}_3=x_3-{Ø}_{3}t$$

(7)

Since each SPE statistic is compiled based on the prediction errors of different classes of measurements, it clearly shows that a given fault is caused by a certain class of measurements. The confidence bound of SPE statistics can be predicted by χ²-distributed approximation: SPE~g.${\chi }_h^2$, in which g and h are the parameters of the χ² distribution, and they are given by [5].

$$gh=mean\left(SPE\right)$$

(8)

$$2g^{2}h=var\left(SPE\right)$$

(9)

3. Two-Phase Reactor–Condenser System with Recycle

The process depicted in Figure 1 includes a two-phase reactor and condenser [6]. Reactants A and B are introduced into the reactor at molar flow rates F_A and F_B and temperatures T_A and T_B, respectively, in the vapour and liquid phases. Reactant A diffuses into the liquid phase at rate N_A1, where an exothermic reaction occurs, which is given by Equation (10).

A + B → 2C

(10)

Product C diffuses into the vapour phase at a rate Nc1, whereas reactant B is non-volatile. The interphase mass transfer resistance is assumed to be minimal, and the Arrhenius equation provides the reaction rate in the bulk liquid phase, which is given by Equation (11).

$$r_A=k_{10}\exp \left(\frac{-E_a}{R{T}_1}\right)M_1^l\rho x_{A1}{x}_{B1}$$

(11)

where r_A is the rate at which reactant A is consumed at temperature T₁. The preexponential factor and activation energy are denoted by k₁₀ and E_a, respectively. $M_1^l$ is the liquid molar holdup in the reactor, and $\rho$ is the liquid density. x_A1 and x_B1 are A and B mole fractions in the liquid phase. For the sake of simplicity, heat capacity, density, and molar heat of vaporisation are considered to be constant and equal for all species. The liquid and vapour phases are suitable combinations. The liquid stream from the reactor is withdrawn at a constant flow rate F_1l, while the vapour stream enters the condenser at a flow rate F_1v. The vapour in the condenser is cooled to T₂ to improve product purity by eliminating reactant A from the liquid.

The reactant A-rich liquid phase in the condenser is returned to the reactor at a flow rate of F_2l, while the product vapour phase departs the condenser at a flow rate of F_2v and a composition of y_A2.

Equations (12)–(29) give a detailed differential algebraic equation (DAE) model used to train the MPPCA model for data generation.

$${\dot{M}}_1^l=F_B-F_{1l}+F_{2l}+N_{A1}-N_{C1}$$

(12)

$${\dot{x}}_{A1}=\left(\frac{1}{M_1^l}\right)\left[-F_B{x}_{A1}+F_{2l}\left(x_{A2}-x_{A1}\right)+N_{A1}\left(1-x_{A1}\right)+N_{C1}{x}_{A1}-r_A\right]$$

(13)

$${\dot{x}}_{B1}=\left(\frac{1}{M_{1l}}\right)[F_B\left(1-x_{B1}\right)-F_{2l}{x}_{B1}-N_{A1}{x}_{B1}+N_{C1}{x}_{B1}-r_A$$

(14)

$${\dot{M}}_1^v=F_A-F_{1v}-N_{A1}+N_{C1}$$

(15)

$${\dot{y}}_{A1}=\left(\frac{1}{M_1^v}\right)\left[F_A\left(1-y_{A1}\right)-N_{A1}\left(1-y_{A1}\right)-N_{C1}{y}_{A1}\right]$$

(16)

$$\begin{gathered} {\dot{T}}_1=\left(\frac{1}{M_1^l+M_1^v}\right)[F_A\left(T_A-T_1\right)+F_B\left(T_B-T_1\right)+F_{2l}\left(T_2-T_1\right) \\ +\left(N_{A1}-N_{C1}\right)\frac{\Delta H^v}{C_P}-\frac{Q_1}{C_P}+r_A\left(\frac{-\Delta H_r}{C_P}\right)] \end{gathered}$$

(17)

$${\dot{M}}_2^l=N_{A2}+N_{C2}-F_{2l}$$

(18)

$${\dot{x}}_{A2}=\left(\frac{1}{M_2^l}\right)\left[N_{A2}\left(1-x_{A2}\right)-N_{C2}{x}_{A2}\right]$$

(19)

$${\dot{M}}_2^v=F_{1v}-F_{2v}-N_{A2}-N_{C2}$$

(20)

$${\dot{y}}_{A2}=\left(\frac{1}{M_2^v}\right)\left[F_{1v}\left(y_{A1}-y_{A2}\right)-N_{A2}\left(1-y_{A2}\right)+N_{C2}{y}_{A2}\right]$$

(21)

$${\dot{T}}_2=\left(\frac{1}{M_2^l+M_2^v}\right)\left[F_{1v}\left(T_1-T_2\right)+(N_{A2}+N_{C2}\right)\frac{\Delta H^v}{C_p}-\frac{Q_2}{C_P}]$$

(22)

$$0=N_{A1}-k_{A}a\left(y_{A1}-y_{A1}^{*}\right)\frac{M_1^l}{\rho }$$

(23)

$$0=N_{C1}-k_{C}a\left(y_{c1}^{*}-\left(1-y_{A1}\right)\right)\frac{M_1^l}{\rho }$$

(24)

$$0=N_{A2}-k_{A}a\left(y_{A2}-y_{A2}^{*}\right)\frac{M_2^l}{\rho }$$

(25)

$$0=N_{C2}-k_{C}a\ast \left(1-y_{A2}-y_{C2}^{*}\right)\frac{M_2^l}{\rho }$$

(26)

$$0=P_1\left(V_{1T}-\frac{M_1^l}{\rho }\right)-M_1^{v}R{T}_1$$

(27)

$$0=P_2\left(V_{2T}-\frac{M_2^l}{\rho }\right)-M_2^{v}R{T}_2$$

(28)

$$0=P_1-P_2-\frac{1}{0.09}{(F_{1v})}^{\frac{7}{4}}$$

(29)

The system parameter values are given in

Table 1. TPRCR system parameter.

Parameter	Description	Value	Unit
a	Interfacial mass transfer area/unit liquid holdup	1000	m2/m3
Cp	Molar heat capacity	80	J/mol K
Ea	Activation energy	110	kJ/mol
K	Proportional gain of pressure controller	−8	mol/s atm
K10	Preexponential factor	2.88 × 1011	m3/mol s
ka	Overall mass transfer coefficient for A	0.2	mol/m2 s
kc	Overall mass transfer coefficient for C	0.8	mol/m2 s
M1l	Liquid molar holdup in reactor	14.52	kmol
M2l	Liquid molar holdup in condenser	15	kmol
M1v	Vapour molar holdup in reactor	3.75	kmol
M2v	Vapour molar holdup in condenser	3.90	Kmol
P1	Pressure in reactor	50	atm
P2	Pressure in condenser	48.69	atm
P*	Set point for reactor pressure	50	atm
TA	Temperature of feed A	315	K
TB	Temperature of feed B	300	K
T1	Temperature in reactor	330	K
T2	Temperature in condenser	304.16	K
V1T	Volume of reactor	3	m3
V2T	Volume of condenser	3	m3
$\rho$	Liquid molar density	15,000	mol/m3
$\Delta H_r$	Heat of reaction	−50	kJ/mol
$\Delta H^v$	Heat of vaporization	10	kJ/mol

.

4. Fault Detection Using MPPCA for the TPRCR System

Three types of measurements are used to train the MPPCA model. Fast-rate measurements include temperature, pressure, and flow rates available every second (x₁). Medium-rate measurements include molar holdups available every fifteen seconds (x₂), and slow-rate measurements include mole fractions available every sixty seconds (x₃).

The MPPCA model is trained with 7200 samples of fast-rate measurements, 480 samples of medium-rate measurements, and 120 samples of slow-rate observations. The fault identification capability of the MPPCA approach is assessed using the six categories of faults indicated in

Table 2. Fault description in the TRPCR system.

Fault No.	Fault Type	Fault Introduced (s)
1	Step jump in flow rate of A (FA)	2400
2	Step jump in flow rate of B (FB)	2400
3	Step jump in temperature of A (TA)	2400
4	Step jump in temperature of B (TB)	2400
5	Ramp jump in flow rate of A (0.0004 × t)	2400
6	Ramp jump in temperature of A (0.003 × t)	2400

.

For a fair comparison, all detection models in this work have a level of significance of 0.99 for the SPE and T² statistics.

Table 3. Fault monitoring results using T² and SPE statistics.

Fault No	T2	SPE1	SPE2	SPE3
0	0.021	0.001	0.004	0.0001
1	0.035	0.023	0.09	0.008
2	0.067	0.065	0.011	0.034
3	0.001	0.001	0.001	0.001
4	0.854	0.673	0.765	0.231
5	0.313	0.452	0.023	0.045
6	0.201	0.121	0.111	0.201

shows the false alarm rates for normal data and the missing detection rates for faults, where Fault 0 represents normal test data and that the monitoring results are false alarm rates. The false alarm rate is the fraction of normal data that is interpreted as problem data. Similarly, the missing detection rate is the fraction of the defect data that are treated as normal data. Table 3 shows the monitoring results of all faults using T² and different SPE statistics for the MPPCA model.

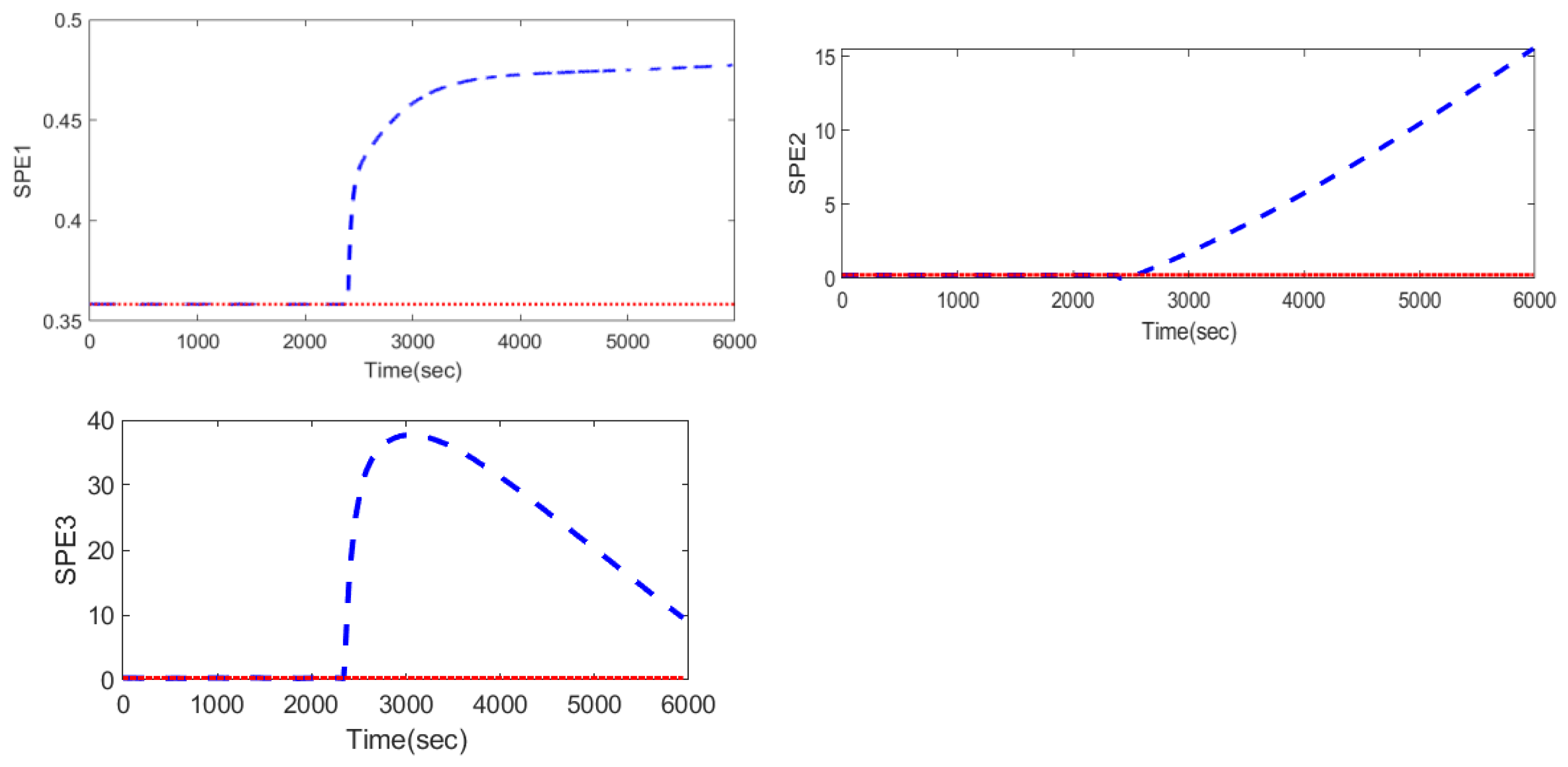
Three different SPE statistics are used to see which fault will have an effect on which SPE statistic. Figure 2 shows SPE statistics for the fault in flow rate of A (F_A), which suggests that this fault affects all three SPE statistics.

5. Conclusions

In this paper, the TPRCR system is modelled as a multi-rate system due to the involvement of qualitative variables, including three different classes of measurements. These measurements are used to develop the MPPCA model using the EM algorithm. This developed MPPCA model is used to detect faults by developing T² and three different SPE statistics for each measurement class. Six different types of faults are used to check the effectiveness of the developed MPPCA model, and, from the monitoring results, we can clearly say that the MPPCA model can detect faults with a high detection rate.