Linear Quadratic Gaussian Design in a Grid-Connected and Islanded Microgrid System for Stability Enrichment †
Abstract
:1. Introduction
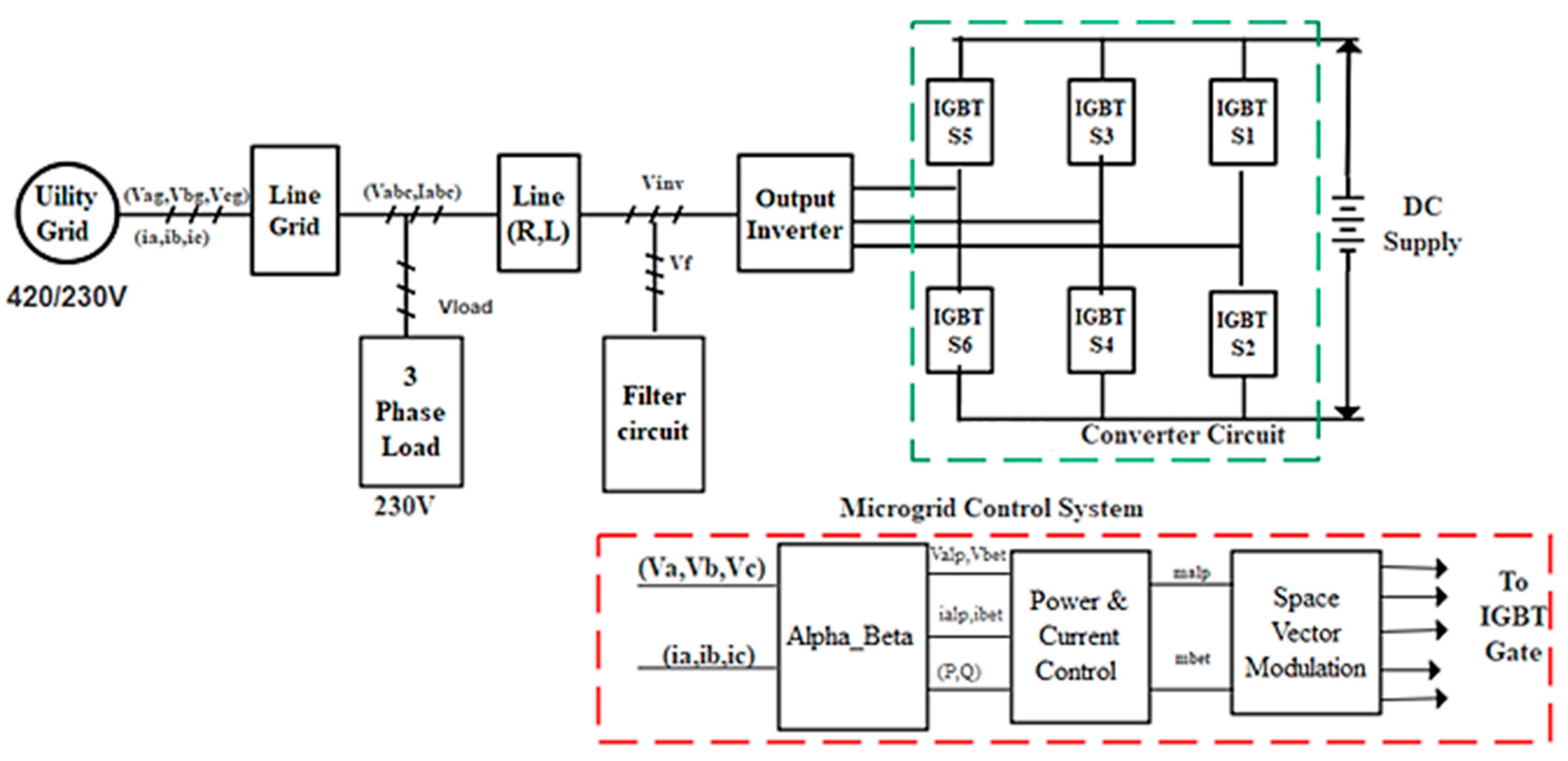
2. Microgrid Mode
2.1. Grid-Connected Mode
2.2. Islanded Mode
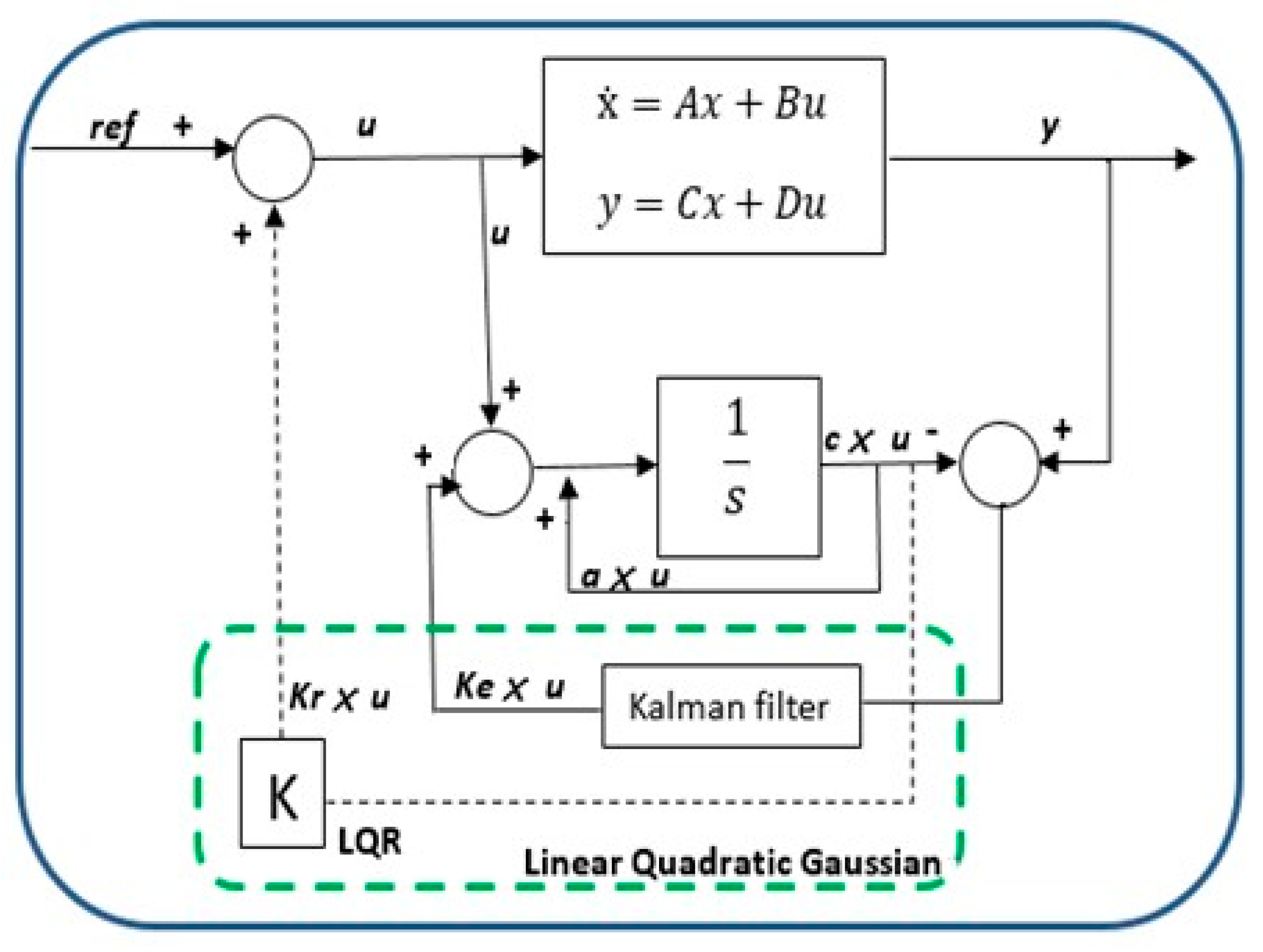
3. Linear Quadratic Controller Design
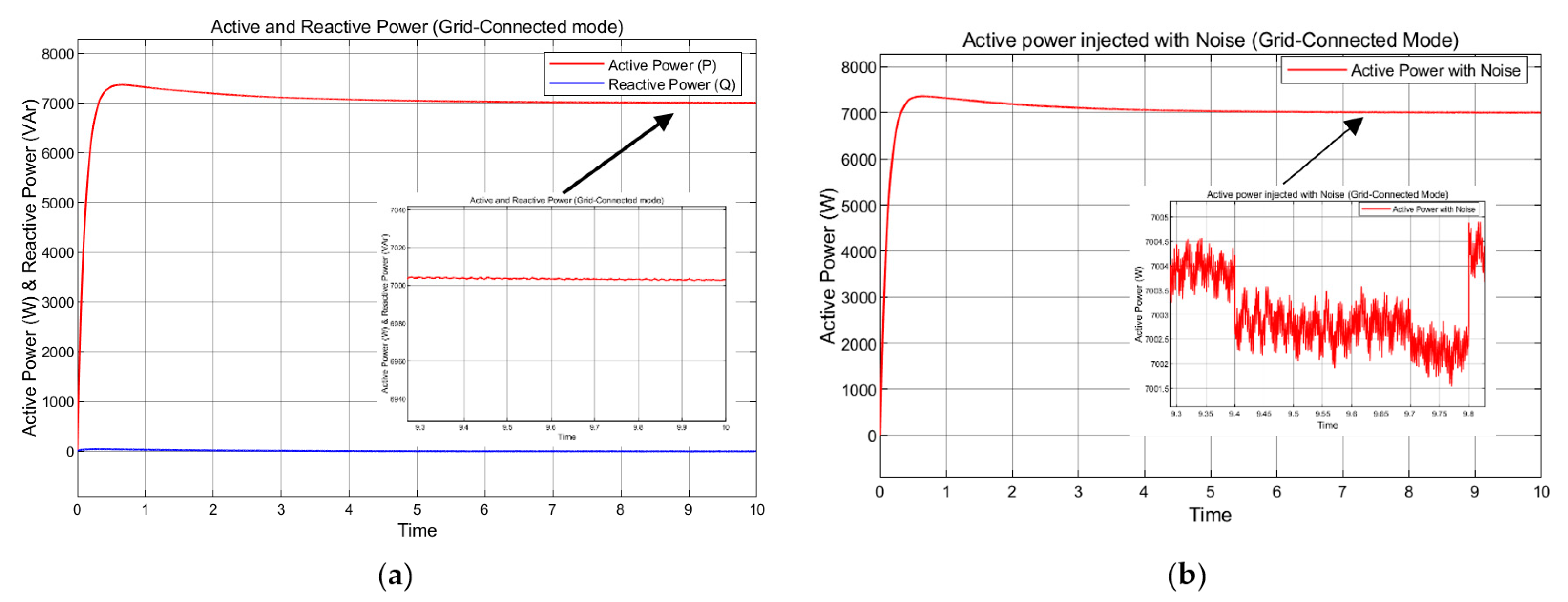
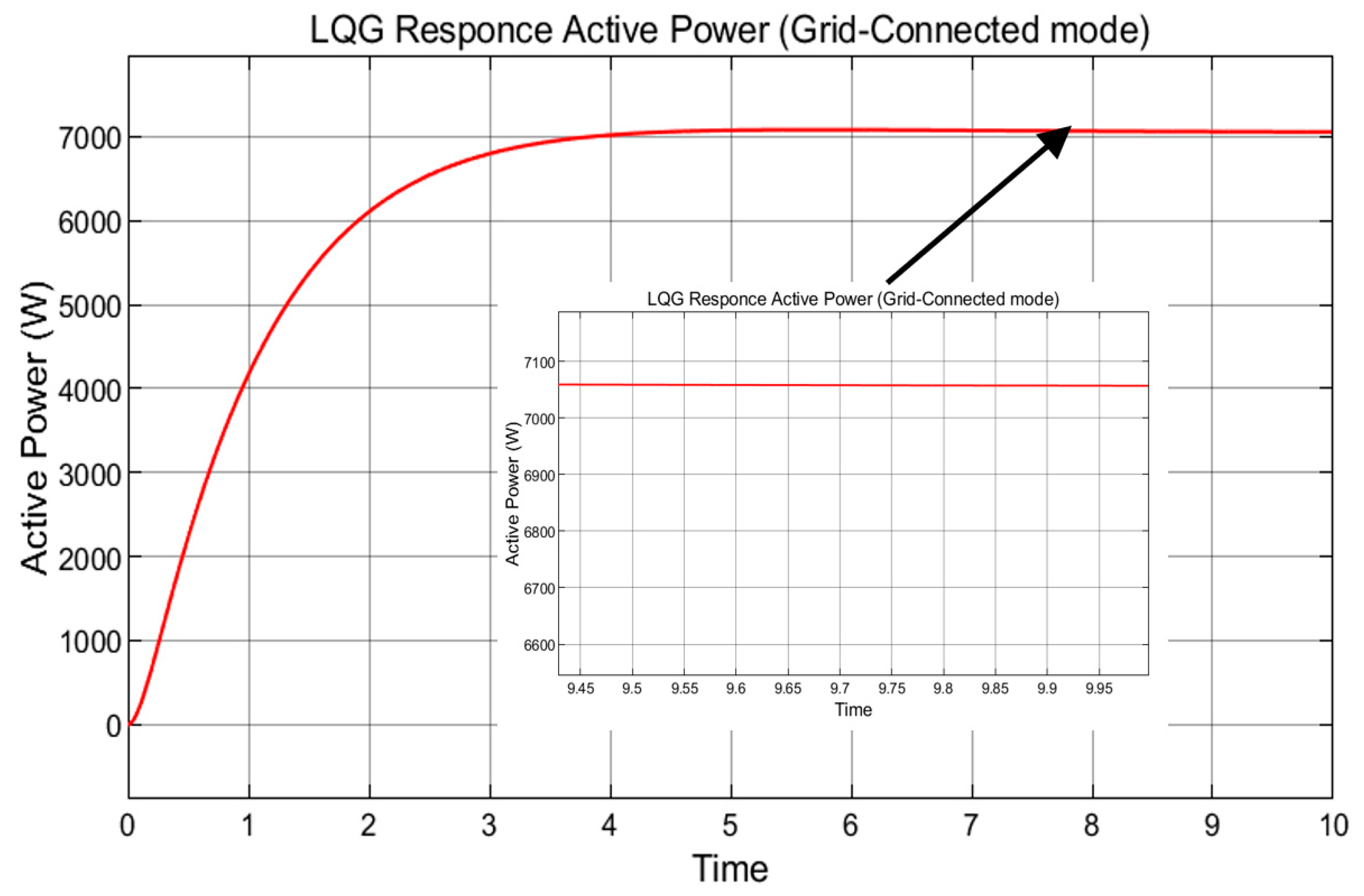
4. Simulation Results
Grid-Connected Mode
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- El-Hawary, M.E. Introduction to Electrical Power Systems; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Cheng, Z.; Duan, J.; Chow, M.-Y. To centralize or to distribute: That is the question: A comparison of advanced microgrid management systems. IEEE Ind. Electron. Mag. 2018, 12, 6–24. [Google Scholar] [CrossRef]
- de Souza, A.C.Z.; Castilla, M. (Eds.) Microgrids Design and Implementation; Springer International Publishing: New York, NY, USA, 2019. [Google Scholar]
- Katiraei, F.; Iravani, R.; Hatziargyriou, N.; Dimeas, A. Microgrids management. IEEE Power Energy Mag. 2008, 6, 54–65. [Google Scholar] [CrossRef]
- Khosrow, M.; Kumar, R. A reliability perspective of the smart grid. IEEE Trans. Smart Grid 2010, 1, 57–64. [Google Scholar]
- Rocabert, J.; Azevedo, G.M.; Luna, A.; Guerrero, J.M.; Candela, J.I.; Rodríguez, P. Intelligent connection agent for three-phase grid-connected microgrids. IEEE Trans. Power Electron. 2011, 26, 2993–3005. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Loh, P.C.; Lee, T.L.; Chandorkar, M. Advanced control architectures for intelligent microgrids—Part II: Power quality, energy storage, and AC/DC microgrids. IEEE Trans. Ind. Electron. 2012, 60, 1263–1270. [Google Scholar] [CrossRef]
- Miret, J.; García de Vicuña, J.L.; Guzmán, R.; Camacho, A. A flexible experimental laboratory for distributed generation networks based on power inverters. Energies 2017, 10, 1589. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Chandorkar, M.; Lee, T.L.; Loh, P.C. Advanced control architectures for intelligent microgrids—Part I: Decentralized and hierarchical control. IEEE Trans. Ind. Electron. 2012, 60, 1254–1262. [Google Scholar] [CrossRef]
- de Andrade, F.; Castilla, M.; Bonatto, B.D. Basic Tutorial on Simulation of Microgrids Control Using MATLAB® & Simulink® Software; Springer Nature: Berlin, Germany, 2020. [Google Scholar]
- Hespanha, J.P. Lecture Notes on LQR/LQG Controller Design. Knowledge Creation Diffusion Utilization. 2005. Available online: http://staff.uz.zgora.pl/wpaszke/materialy/kss/lqrnotes.pdf (accessed on 27 February 2021).
- Se Pa, S.; Yakoob, M.B.; Maruthai, P.; Singaravelu, K.; Duraisamy, N.; Palaniappan, R.D.; Pithai, J.B. Machine Learning Gaussian Process Regression based Robust H-Infinity Controller Design for Solar PV System to Achieve High Performance and Guarantee Stability. Eng. Proc. 2022, 19, 26. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Se Pa, S.; Yakoob, M.B.; Seetharaman, M.; Victor, J.D.; Arumugam, K.; Muthukumaran, S. Linear Quadratic Gaussian Design in a Grid-Connected and Islanded Microgrid System for Stability Enrichment. Eng. Proc. 2023, 37, 65. https://doi.org/10.3390/ECP2023-14672
Se Pa S, Yakoob MB, Seetharaman M, Victor JD, Arumugam K, Muthukumaran S. Linear Quadratic Gaussian Design in a Grid-Connected and Islanded Microgrid System for Stability Enrichment. Engineering Proceedings. 2023; 37(1):65. https://doi.org/10.3390/ECP2023-14672
Chicago/Turabian StyleSe Pa, Sureshraj, Mohamed Badcha Yakoob, Muthuveerappan Seetharaman, Jenita Daniel Victor, Kasthuri Arumugam, and Srimathi Muthukumaran. 2023. "Linear Quadratic Gaussian Design in a Grid-Connected and Islanded Microgrid System for Stability Enrichment" Engineering Proceedings 37, no. 1: 65. https://doi.org/10.3390/ECP2023-14672
APA StyleSe Pa, S., Yakoob, M. B., Seetharaman, M., Victor, J. D., Arumugam, K., & Muthukumaran, S. (2023). Linear Quadratic Gaussian Design in a Grid-Connected and Islanded Microgrid System for Stability Enrichment. Engineering Proceedings, 37(1), 65. https://doi.org/10.3390/ECP2023-14672






