A Data-Driven Approach for Fatigue Damage Prediction in Jointed Plain Concrete Pavement Subjected to Superloads ^†

Abstract

The passage of superloads over the jointed plain concrete pavements (JPCPs) causes signification fatigue damage to the JPCPs. This mainly happens because of their non-standardized loading configurations and high gross vehicle and axle weights. Developing a high-accuracy prediction model for JPCP fatigue damage under superloads is strongly required to complement the mechanistic–empirical (ME) pavement design in aspects of its wide range of dimensions, including number, spacing, and loading of tires and axles. In this study, various data-driven models based on different theoretical approaches, including artificial neural network-based models, generalized additive models, and multiple linear regression models, were constructed using a well-established database derived from finite-element analysis results in order to predict the target response for JPCP fatigue damage when subjected to superloads. The prediction accuracies of these data-driven models were then evaluated to confirm their further applicability to the existing ME pavement design software.

1. Introduction

Fatigue damage in jointed plain concrete pavement (JPCP) is one of the major damage types that traffic loads can induce. Particularly, fatigue damage is often caused by overweight trucks or superloads with gross vehicle or axle weights that exceed a state’s permit limits. Unlike conventional vehicle types, superloads are distinguished from general vehicle types by their non-standardized loading configurations, including the number and spacing of tires and axles, for the purpose of transporting oversized and heavy payloads [1]. Previous studies have suggested using simple empirically based generalized power law theories to describe the nonlinear relationship between pavement damage and traffic loads, such as the fourth power law from the American Association of State Highway Officials Road Test [2], or using different power-law exponents dependent on different pavement structures and loading conditions from follow-up study [3]. As such, new mechanistic-based analysis approach that reflects the characteristics of superloads beyond the scope of general loading configuration is still required. AASHTOWare Pavement Mechanistic-Empirical (ME) Design software, which builds upon the ME pavement design guide [4], has provided ME-based JPCP fatigue damage calculation as a data analysis and back-calculation tool. It has done so by generating the horizontal tensile stresses in a Portland cement concrete (PCC) layer from a series of artificial neural network (ANN)-based models using a database of finite-element analysis (FEA) results produced by using ISLAB 2000 [5]. However, the database used to train the ANN models in this software did not include a wide range of dimensions with respect to superload loading configurations, and so the extrapolation of explanatory variables in terms of loading parameters may lead to inaccurate calculation of JPCP responses when subjected to superloads.

In this study, various data-driven models, including ANN-based models, generalized additive models (GAMs), and multiple-linear regression models, were constructed using a database of FEA results (i.e., the critical horizontal tensile stress at the bottom and top of the PCC slab when subjected to superloads) collected from ISLAB 2005. The prediction accuracy of these data-driven models was evaluated and compared to confirm their further applicability to the existing Pavement ME Design software.

2. Methodology

The FEA results, including the critical horizontal tensile stress in PCC slab depending on different JPCP structures and superloads, used as database to train and test the prediction models, were collected from the same author’s previous study [1]. The experimental design for FEA and data-driven modeling is briefly summarized in Table 1. Note that each critical tensile stress of PCC slab was calculated from pre-determined critical loading locations differentiated by superload types and JPCP structures.

Table 1. Experimental matrix of JPCP structures for FEA and data-driven modeling [1].

Input Variables (Explanatory Variables)	Value	Unit
PCC layer thickness	200, 230, 250	mm
Composite modulus of subgrade reaction	14 (spring), 33 (summer), 33 (fall), 68 (winter)	MPa/m
Transverse joint spacing	4.5 for 200 mm and 230 mm PCC layer thickness 5 for 250 mm PCC layer thickness 6 for 200 mm, 230 mm, and 250 mm PCC layer thickness	m
Coefficient of thermal expansion	7.7, 9.4	10−6/°C
Temperature gradients	−0.09, −0.04, 0, 0.04, 0.09	°C/mm
Elastic modulus of PCC layer	27,500	MPa
Traffic loads	IoH 1: 18 types × 4 payload levels (100%, 75%, 50%, 0%) = 72 cases SHL 2: 16 types × 4 payload levels (100%, 75%, 50%, 0%) = 64 cases	-

Note: Individual input variables applied to non-dimensional variables can have a wider range of values than those indicated in the table depending on other variables. ¹ IoH = implements of husbandry; representative superload types for transporting agricultural products, slurry, or water, including grain carts, manure tankers, agricultural trailers and trucks. ² SHL = superheavy load; representative superload types for transporting wind turbines or engine blocks, including drop-deck types, and single-row and dual-row modular types.

A database collected from FEA using ISLAB 2005 was then used to train and test surrogate data-driven models based on different theoretical approaches. (i) ANN-based models, (ii) GAMs, and (iii) multiple linear regression models were constructed in this study to compare and analyze each of their prediction accuracies. The data and statistical sets of data-driven models and a brief introduction to each approach are summarized and listed in Figure 1. Please refer to previous studies for a detailed theoretical background on each data-driven approach similarly applied to flexible pavement cases [6] and further application of GAM to earthquake engineering [7]. As can be seen from Figure 1, a total of 24 GAMs varying by three statistical distributions, two link functions, and two spline bases, and a total of 24 ANN models consisting of three different numbers of hidden layers and four different numbers of neurons per each layer were constructed for comparative evaluation.

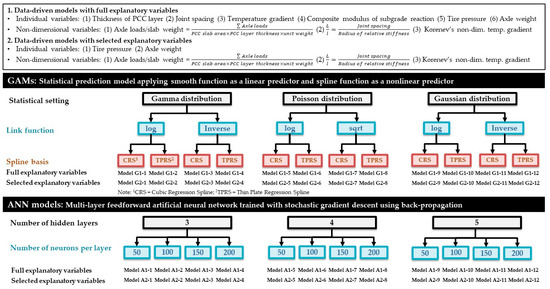
Figure 1. Data and statistical sets of data-driven models.

3. Prediction Accuracy of Data-Driven Models

All prediction models shown in Figure 1 were evaluated by splitting the original dataset into 70 percent and 30 percent portions to constitute a training set and a testing set. Figure 2 and Figure 3, respectively, show the prediction accuracy of each model for the critical horizontal stress at the bottom and top of the PCC slab. It can be easily confirmed from the figures that ANN models outperform both GAMs and multiple regression models for all superload types when determining the best prediction model for each prediction approach and superload type. In the case of an agricultural trailer or truck, GAM exhibits a lower prediction accuracy for the critical horizontal stress at the top of the PCC slab than the multiple linear regression model due to the relatively small number of data points of the training dataset collected for those superload types.

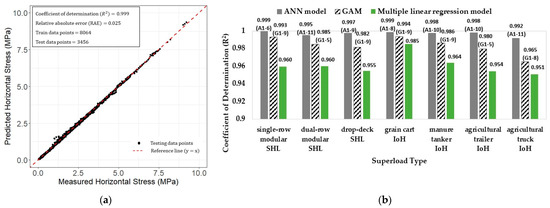
Figure 2. Prediction accuracy evaluation in case of: (a) ANN model A1–6 predicting critical horizontal stress at the bottom of the PCC slab when subjected to single-row modular-type SHL; (b) models showing the best prediction accuracy for each prediction approach and superload type.

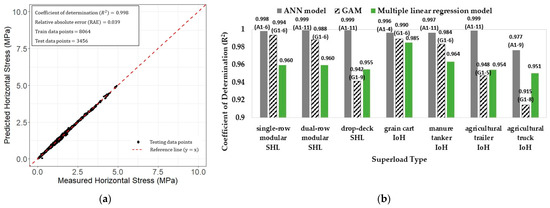
Figure 3. Prediction accuracy evaluation in case of: (a) ANN model A1–6 predicting critical horizontal stress at the top of the PCC slab when subjected to single-row modular-type SHL; (b) models showing the best prediction accuracy for each prediction approach and superload type.

4. Conclusions

Overall, ANN-based prediction models exhibited better accuracy than GAMs or multiple regression models in predicting critical horizontal stress at both the bottom and top of the PCC layer in JPCPs under superload conditions. Further studies are needed to determine the prediction accuracy evaluation of other deep learning algorithms for superload issues.