Holography with Incoherent Light †
Abstract
:1. Introduction
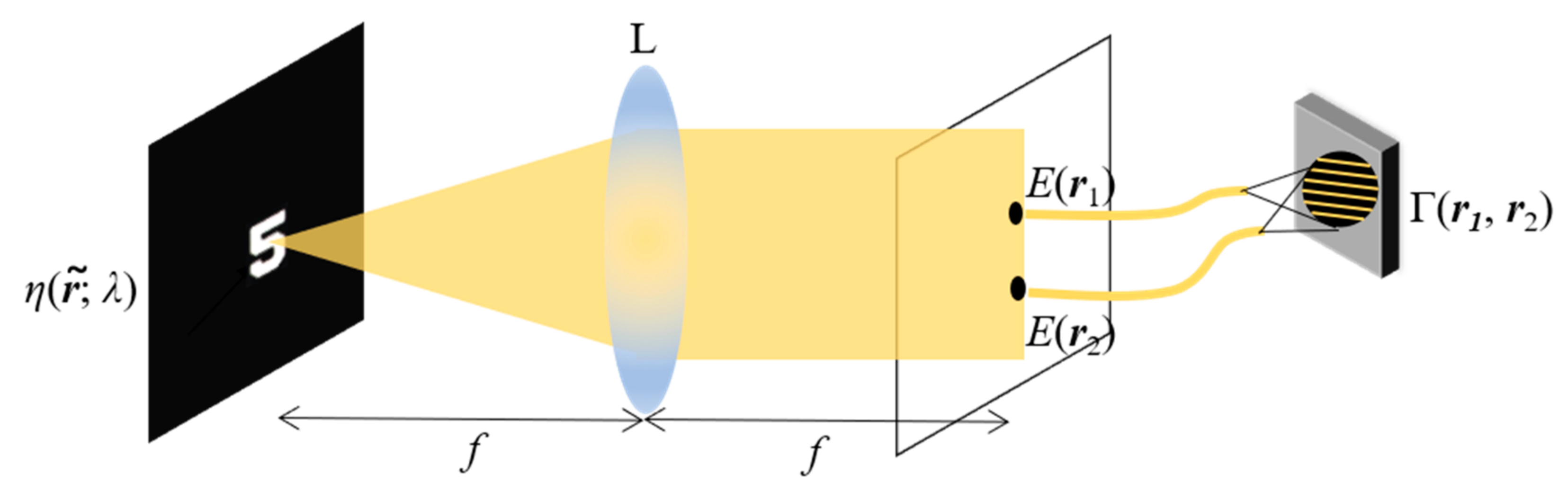
2. Principle
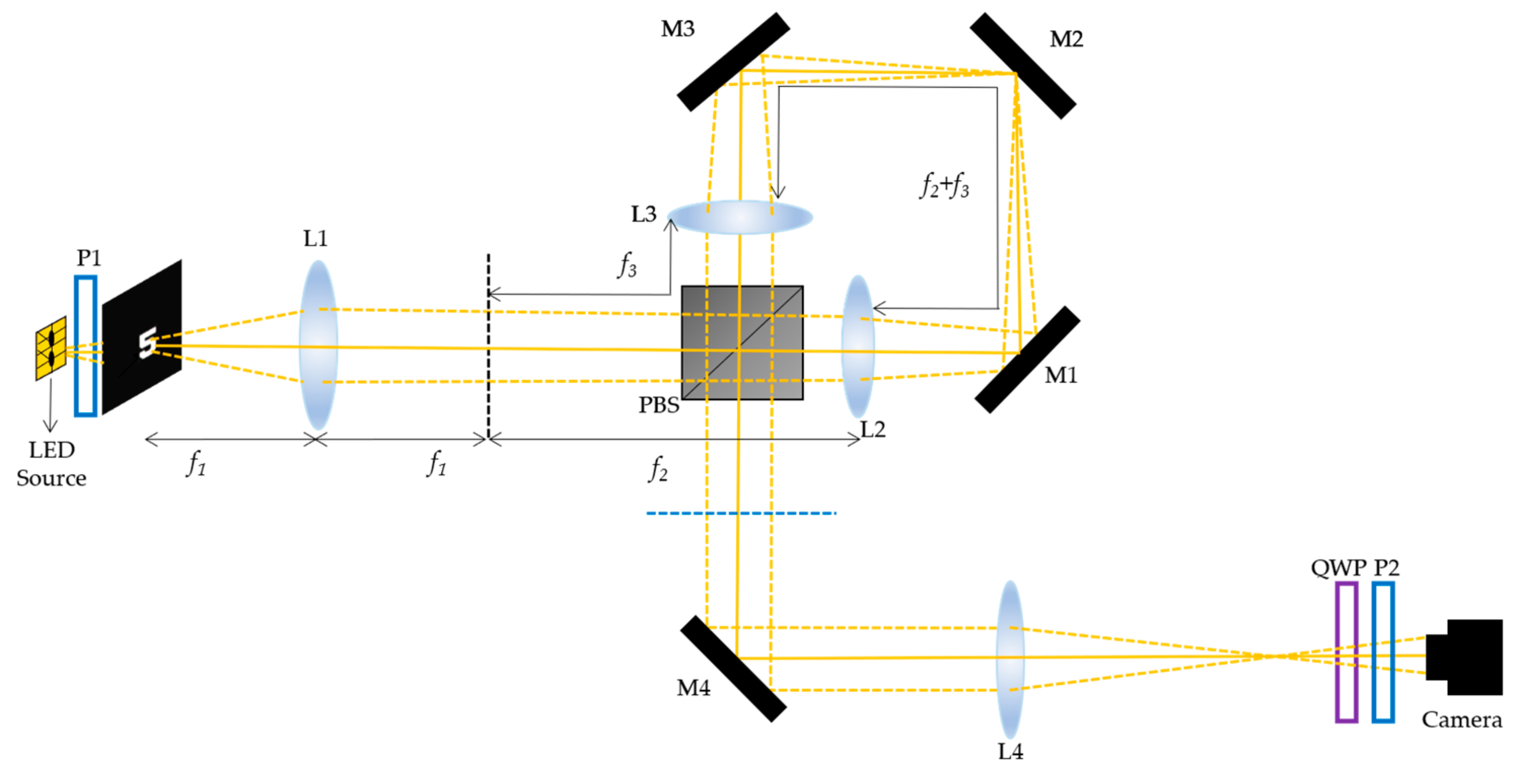
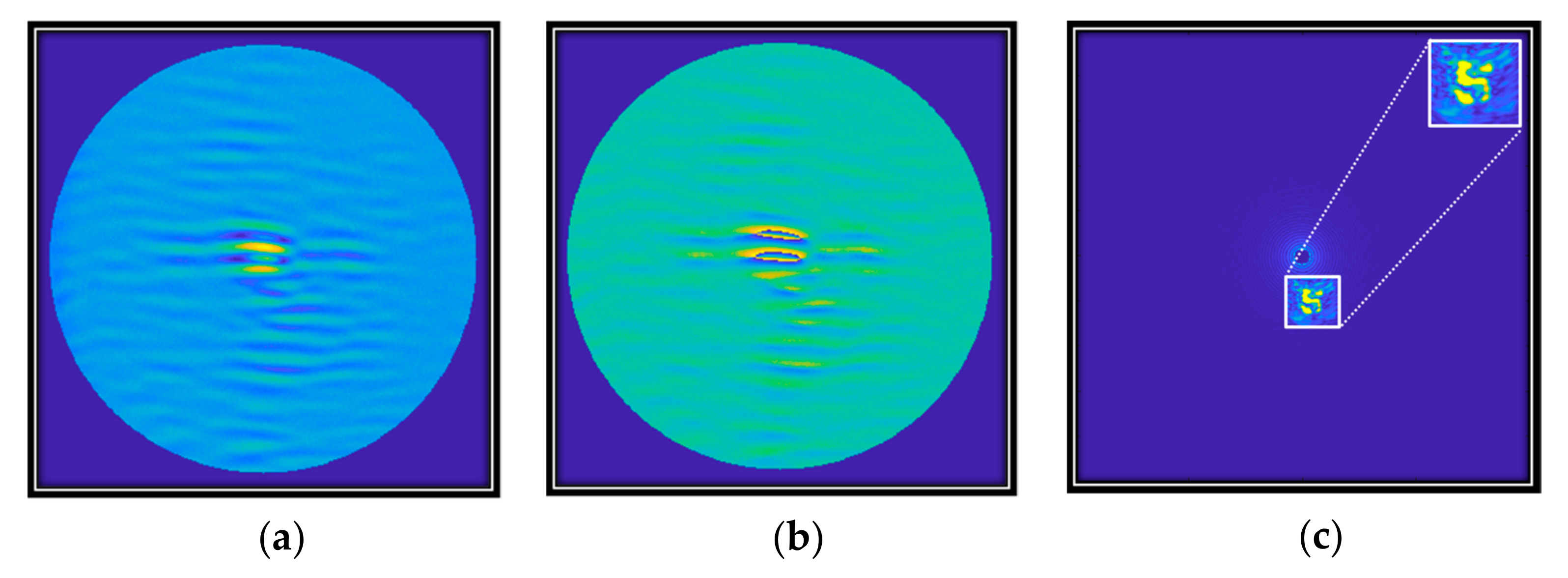
3. Experiment and Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gabor, D. A new microscopic principle. Nature 1948, 161, 777–778. [Google Scholar] [CrossRef]
- Hendry, D. Digital Holography: Digital Hologram Recording, Numerical Reconstruction and Related Techniques; Schnars, U., Jueptner, W., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; ISBN 354021934-X. [Google Scholar]
- Lee, W.H. Sampled Fourier transform hologram generated by computer. Appl. Opt. 1970, 9, 639–643. [Google Scholar] [CrossRef]
- Considine, P.S. Effects of coherence on imaging systems. J. Opt. Soc. Am. 1966, 56, 1001–1009. [Google Scholar] [CrossRef]
- Mills, J.P.; Thompson, B.J. Effect of aberrations and apodization on the performance of coherent optical systems. II. Imaging. J. Opt. Soc. Am. 1986, 3, 704–716. [Google Scholar] [CrossRef]
- Rosen, J.; Brooker, G. Digital spatially incoherent Fresnel holography. Opt. Lett. 2007, 32, 912–914. [Google Scholar] [CrossRef] [PubMed]
- Vijayakumar, A.; Kashter, Y.; Kelner, R.; Rosen, J. Coded aperture correlation holography—A new type of incoherent digital holograms. Opt. Express 2016, 24, 12430–12441. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Zhang, H.; Zhang, W.; Jin, G.; Cao, L.; Barbastathis, G. Single-shot lensless imaging with fresnel zone aperture and incoherent illumination. Light Sci. Appl. 2020, 9, 53. [Google Scholar] [CrossRef] [PubMed]
- Naik, D.N.; Ezawa, T.; Singh, R.K.; Miyamoto, Y.; Takeda, M. Coherence holography by achromatic 3-D field correlation of generic thermal light with an imaging Sagnac shearing interferometer. Opt. Express 2012, 20, 19658–19669. [Google Scholar] [CrossRef] [PubMed]
- Naik, D.N.; Pedrini, G.; Osten, W. Recording of incoherent-object hologram as complex spatial coherence function using Sagnac radial shearing interferometer and a Pockels cell. Opt. Express 2013, 21, 3990–3995. [Google Scholar] [CrossRef] [PubMed]
- Roy, M.; Svahn, P.; Cherel, L.; Sheppard, C.J. Geometric phase-shifting for low-coherence interference microscopy. Opt. Lasers Eng. 2002, 37, 631–641. [Google Scholar] [CrossRef]
- Hariharan, P.; Oreb, B.F.; Eiju, T. Digital phase-shifting interferometry: A simple error-compensating phase calculation algorithm. Appl. Opt. 1987, 26, 2504–2506. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gautam, A.; T S, A.; Naik, D.N.; Narayanmurthy, C.S.; Singh, R.; Singh, R.K. Holography with Incoherent Light. Eng. Proc. 2023, 34, 5. https://doi.org/10.3390/HMAM2-14111
Gautam A, T S A, Naik DN, Narayanmurthy CS, Singh R, Singh RK. Holography with Incoherent Light. Engineering Proceedings. 2023; 34(1):5. https://doi.org/10.3390/HMAM2-14111
Chicago/Turabian StyleGautam, Akanksha, Athira T S, Dinesh N. Naik, C. S. Narayanmurthy, Rajeev Singh, and Rakesh Kumar Singh. 2023. "Holography with Incoherent Light" Engineering Proceedings 34, no. 1: 5. https://doi.org/10.3390/HMAM2-14111
APA StyleGautam, A., T S, A., Naik, D. N., Narayanmurthy, C. S., Singh, R., & Singh, R. K. (2023). Holography with Incoherent Light. Engineering Proceedings, 34(1), 5. https://doi.org/10.3390/HMAM2-14111





