1. Introduction
One of the promising directions of improving the efficiency of solving global search problems is the development of hybrid metaheuristic algorithms (HMHA) and technology of HMHA adaptation to the peculiarities of the applied problem being solved. The main goal of the MHA hybridization is to ensure a balance of global and local search efficiencies and, as a result, to achieve a synergistic effect by combining the positive properties of the combined algorithms.
Currently, a significant number of MHA hybridization methods have been developed. In [
1,
2,
3], the basic principles of MHA hybridization and classification features that are advisable to use in the construction and comparative analysis of various HMHAs are discussed. In particular, a one-level classification of hybridization models is proposed in [
1]. According to those classifications, there are three types of hybrid algorithms: embedded algorithms, preprocessor/postprocessor algorithms and co-algorithms. In [
2], a two-level classification is proposed, using the types of hybridized algorithms and decomposition types of the search space as taxonomic features. In [
3], the most complete four-level classification of HMHAs is proposed, based on the following taxonomic features: a type of hybridized algorithm; a gibridization level; an execution order; and a control strategy.
In [
4], based on a comparative analysis, it is shown that the HMHA classifications discussed above have some intersections, complement each other, and collectively cover almost all currently known HMHA models. Special attention is paid to the study of MHA hybridization possibilities for solving global optimization problems. it is shown that the sequential high-level embedded hybridization model (SHLEH-model) is widely used to solve global optimization problems. This model is usually based on a combination of global search population algorithms and local search algorithms (generally, not populational). A distinctive feature of the SHLEH-model of MHA is that the local search algorithm is an embedded component of the global search populational algorithm. With its help, each agent coordinates in the current population are improved. A new population is formed based on the improved coordinates of each agent in the current population. At the same time, a significant autonomy of the combinable algorithms takes a place. Currently, a large number of high-level embedded hybridization examples of populational algorithms with local optimization algorithmsare known. In particular, memetic algorithms are implemented based on SHLEH-models [
5,
6]; hybrid evolutionary algorithms [
7,
8]; hybrid continuous orthogonal ant colony algorithms using orthogonal search methods in the region selected for each ant [
9,
10]; modifications of a continuously interacting ant colony hybrid algorithm using a combination of global search by an ant algorithm with local search algorithms of a deformable Nelder–Mead polyhedron and dynamic simplex [
11], etc.
Thus, hybrid metaheuristic search algorithms implemented on the basis of SHLEH-models generally provide high efficiency in solving global optimization problems. An important advantage of the SHLEH-models of MHAs is also the possibility of their effective parallelization.
However, all the above-mentioned HMHAs are fundamentally finite-dimensional and in their existing form do not allow us to effectively solve the problems of dynamical systems control multicriteria optimization, which in the original formulation are infinite-dimensional. This circumstance determines the relevance of the development of new HMHA-models, a priori focused on solving infinite-dimensional global optimization problems.
2. The Problem Statement of the Dynamic System Program Control Multicriteria Synthesis
We suggest that the a controlled dynamic system mathematical model is described by a system of nonlinear ordinary differential equations
In (1) is the vector of the system state; —given nonlinear; n—dimensional vector function; —vector of the system control; —initial conditions.
The control selection is subject to restrictions
of the form
where
is the Hilbert space of
-dimensional functions, the square of which we integrate on a fixed interval
(hereinafter the entry
will mean
as an element of the functional space, and
is the value at a time
t).
The efficiency of the system (1) controlling under constraints (2) is estimated by a vector criteria
, whose components are Frechet differentiable functionals of the form
It is necessary to define a program control of the system (1) that satisfies the restrictions (2) and minimizes the values of the components of the vector objective functional (3).
The peculiarity of the statement (1)–(3) is that it is an infinite-dimensional nonlinear multicriteria optimization problem with non-convex objective functionals.
4. Multicriteria Optimization of a Bioreactor Program Control Law
Consider a biotechnological process (BTP) occurring in a bioreactor. A bioreactor is a container with reproducing microorganisms, a solution of salts and simple organic compounds, into which a sterile nutrient medium continuously enters, and part of the contents, including living organisms, is constantly removed. It is assumed that the mathematical model of BTP is given in the form of a system of nonlinear ordinary differential equations characterizing the dynamics of the development of a two-age population of bacteria in a dimensionless form
In the considered BTP model, Equations (4)–(7) describe the dynamics of the development of a two-age population of bacteria in a dimensionless form; (8) the equations of the measured output; and (9) initial conditions. The following designations are used:
—the state vector of the system;
,
—the relative concentrations of the substrate that ensures the growth of “young” and division of “old” cells, respectively;
,
—relative concentrations of “young” and “old” cells, respectively;
—the vector of the measured output of the system;
—the control vector;
,
—the relative rates of entry of the nutrient substrate into the cultivator, ensuring the growth of “young” and division of “old” cells, respectively;
—the relative velocity of the toque in the cultivator; and
—a limited closed set of the form
—quantitative requirements of the microorganism in food;
,
—the maximum and minimum time interval (without feeding with substrates and with maximum feeding with substrate), respectively, necessary for a young cell to change its properties and transition to the phase of development of an old cell;
,
—the maximum and minimum time interval (without feeding with substrates and with maximum feeding with substrate), respectively, required for the old cell to start the division process;
q—the number of descendants after division of one cell (it is genetically inherited and does not depend on the conditions of cultivation);
—the maximum rate of absorption of the substrate by microorganisms;
—the value of the saturation function is equivalent to the Michaelis–Menten constant, numerically equal to the concentration of the substrate, at which the growth rate of the culture is equal to half the maximum rate.
The efficiency of system control (4)–(9) will be evaluated by a vector criteria
, the components of which are functionals differentiable by Frechet:
In (11), (12) characterize an etalon BTP mode.
It is required to determine the program control of the system (4)–(9) with restrictions on the control vector (10), minimizing the values of the components of the vector functional (11), (12).
Model parameters. The computational experiment was carried out at the following values of the model (4)–(12) parameters: , , , , , , , , , ; modeling interval, ; .
To solve the problem (4)–(12), a hybrid evolutionary algorithm of multicriteria optimization based on a transdimensional search model was used, where .
4.1. Global Evolutionary Multicriteria Search
Perform parameterization of the vector law of program control
in the form of
, when
,
,
. To accomplish this this, on the interval
a grid
is built. The parameterized program control law is represented as natural cubic splines
, for which the conditions
are met at the nodal points.
Thus, the vector of control parameters is represented as , where . Next, the problem of finite-dimensional multicriteria optimization is solved. The polyhedral cone of dominance is given as a function of uncertainty intervals of the vector criteria components weighting coefficients.
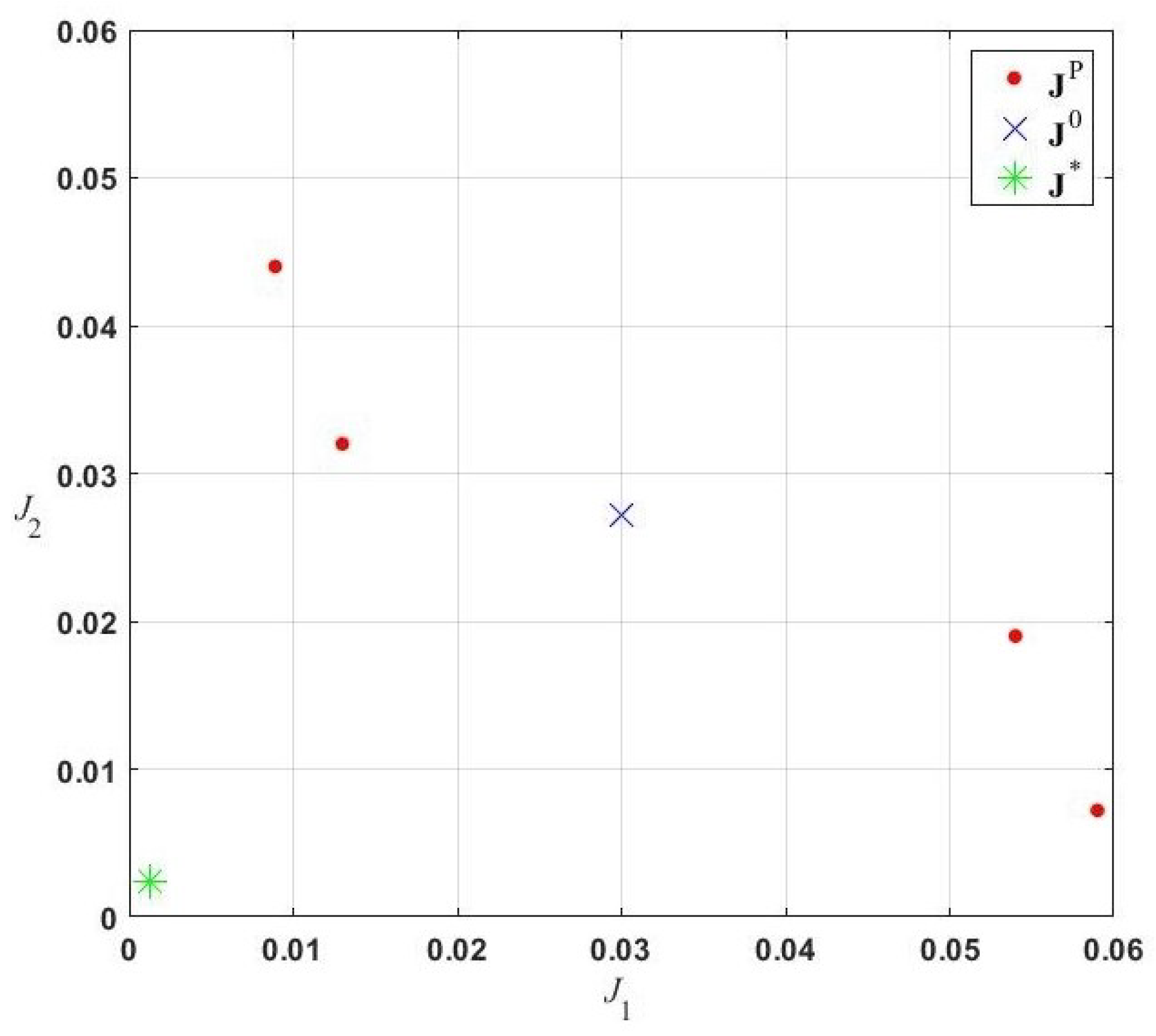
Figure 1 shows the results of the application of the evolutionary algorithm of multicriteria optimization with respect to the polyhedral dominance cone: the points set
is a discrete approximation of
-optimal solutions set in the problem (4)–(12). The polyhedral dominance cone
is given as a function of uncertainty intervals of the vector criteria components weighting coefficients. The uncertainty intervals of the vector criteria components weighting coefficients is given as a set:
The matrix of the dominance cone
The points coordinates of the set
in the criterion space are presented in the
Table 1. Based on the Hermeyer criterion, point No 3 is chosen as the initial approximation
for the implementation of the local multicriteria search stage. As can be seen from
Table 1, the solution
is characterized by the most balanced component values of the vector criteria.
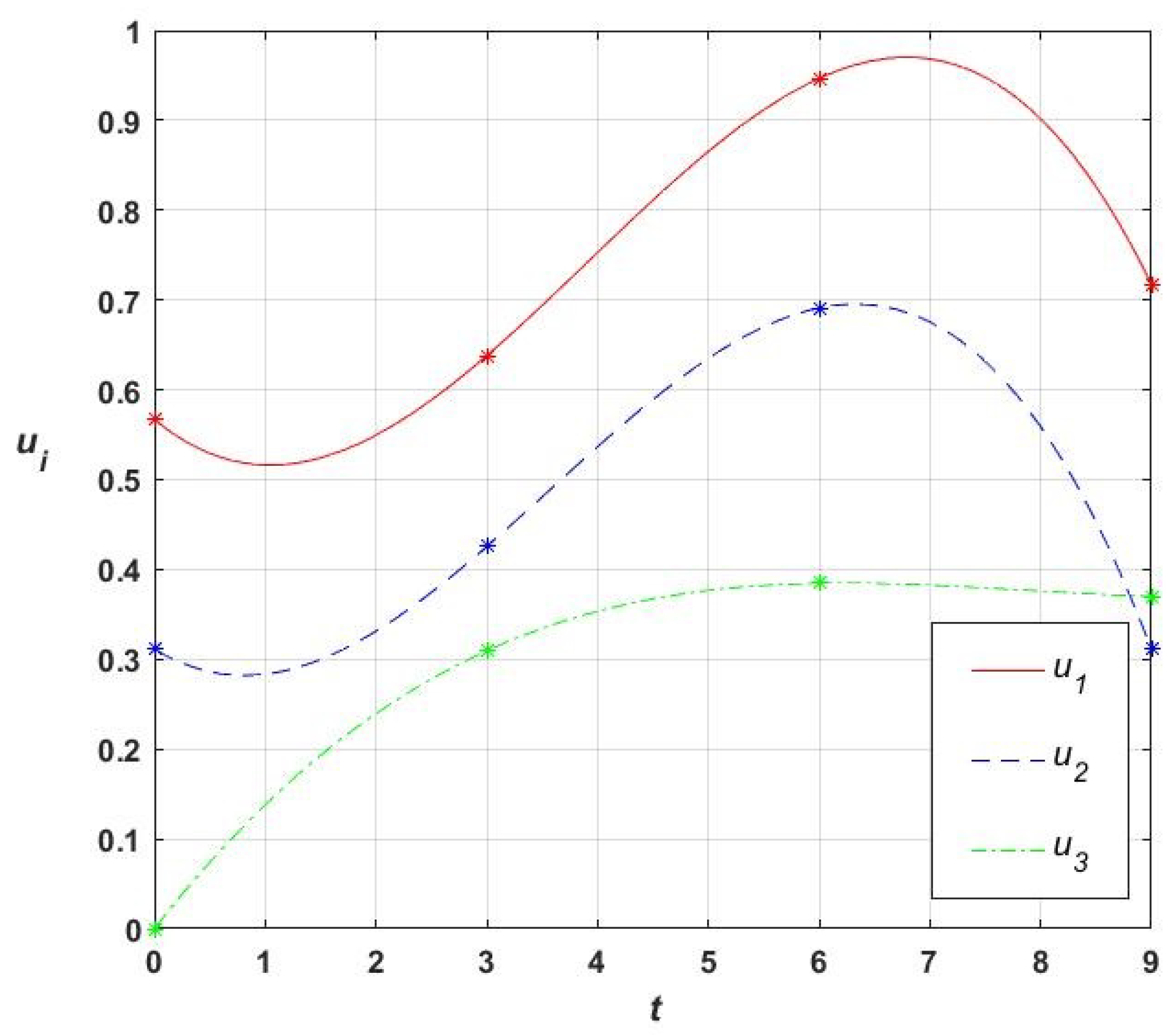
The point
corresponds to the program control
, where
is the vector of control parameters:
The components of the subvector
are the nodal points of the natural cubic spline
,
. The graphs of the components of the program control law
are shown in
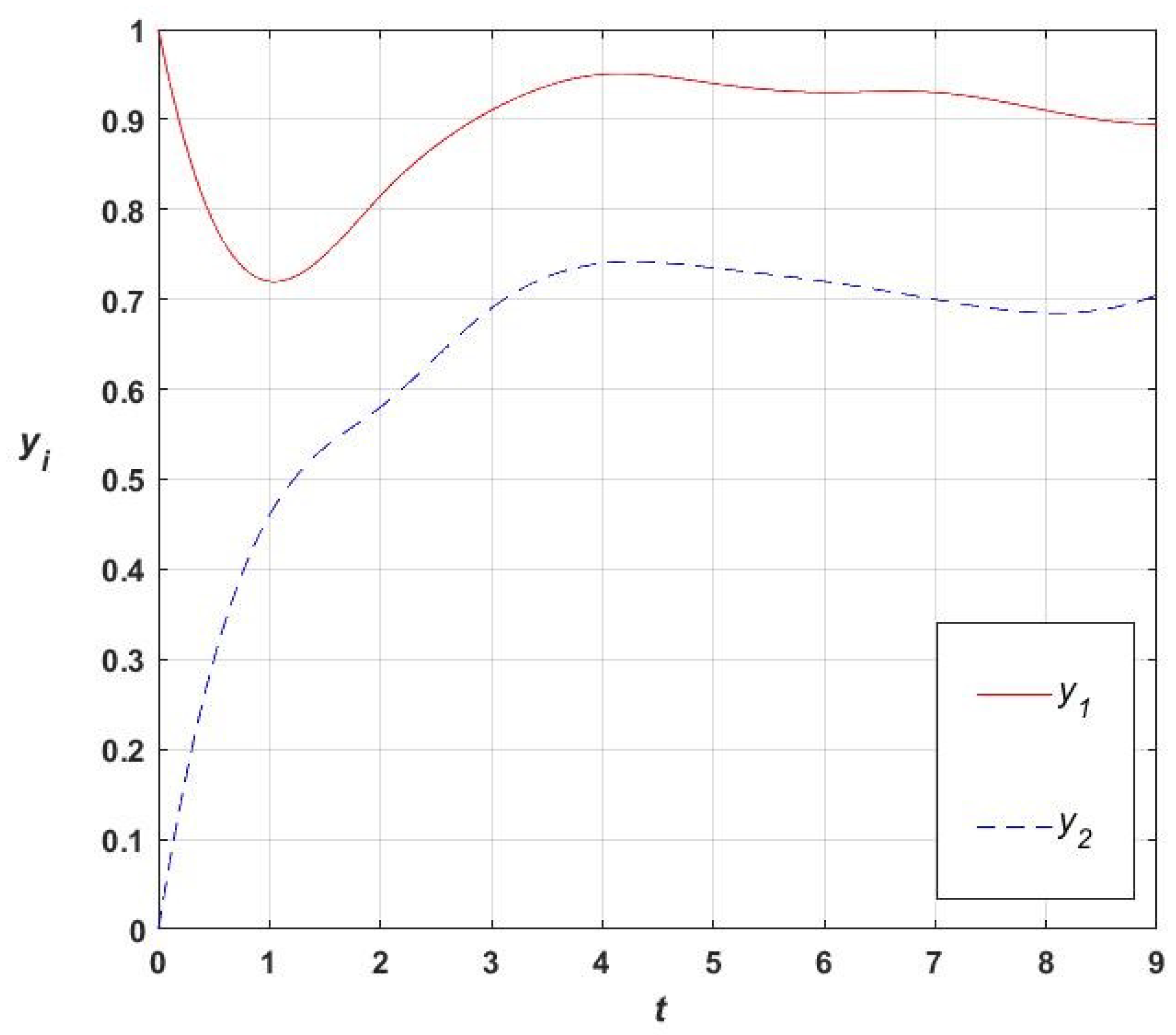
Figure 2. The corresponding trajectory
is shown in the
Figure 3.
4.2. Local Evolutionary Multicriteria Search
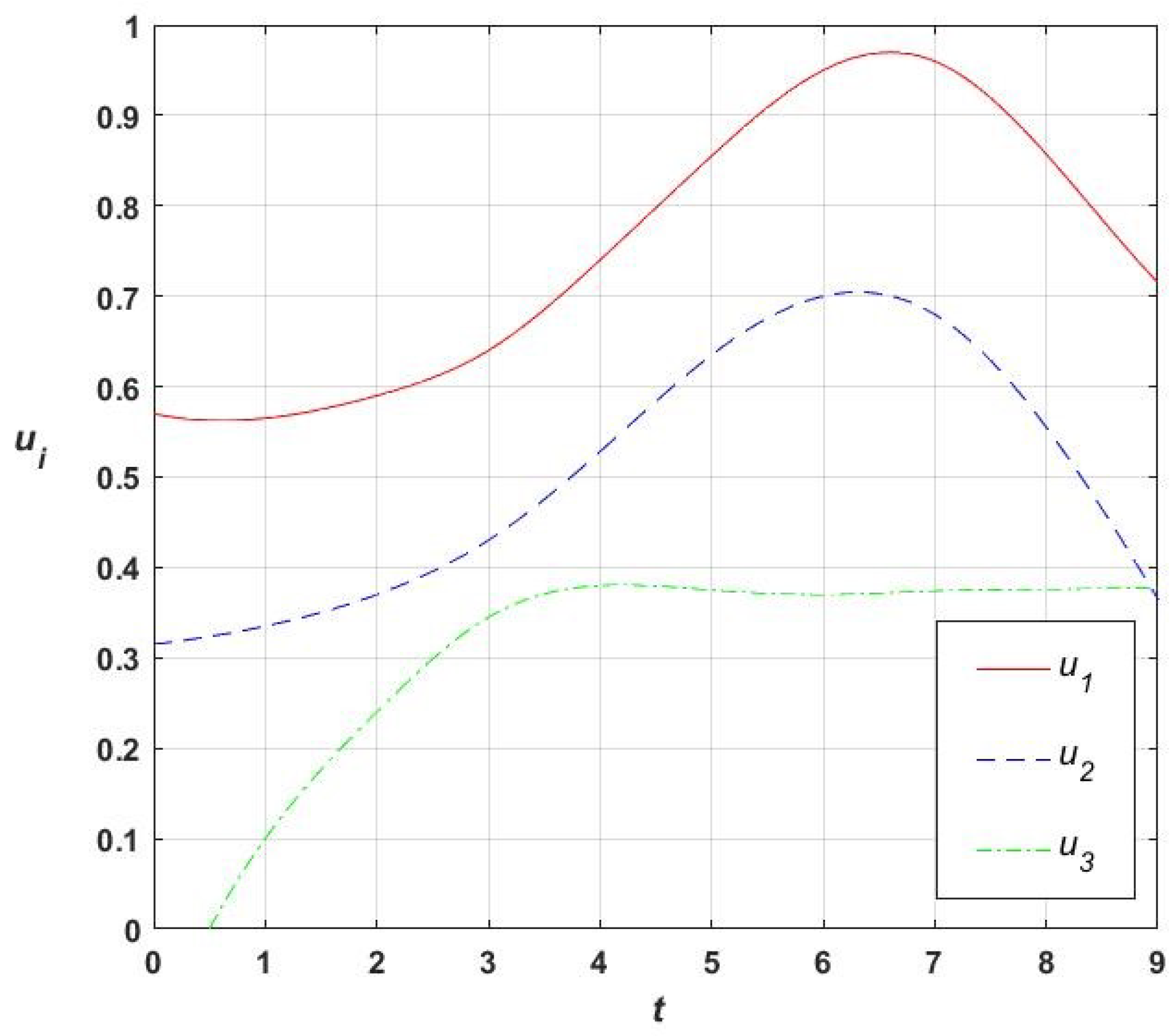
The clarifying search for the optimal law of program control is performed using an evolutionary multicriteria algorithm of feasible directions, in which the degree of the approximating functional of constraints [
13] p = 3. As a result, the optimal control law of the system
is obtained, the form of which is shown in
Figure 4. The corresponding optimal trajectory
is shown in
Figure 5. The optimal value of the vector criteria
is also shown in
Figure 1.
4.3. Comparative Analysis of Transdimensional Search Models
Computational experiments were carried out with various transdimensional search
-models. The results of computational experiments are presented in
Table 2.
In each experiment, the initial approximation for the local multicriteria search stage is formed from the vector obtained at the global multicriteria search stage based on the transdimensional -transition. The transdimensional -transition is implemented using the following algorithm.
Transdimensional -transition algorithm.
Step 1. Convert the time grid into a time grid , , which is obtained from the original one by dividing each interval into two equal parts. The values of the transfer transition parameters have the following values: , .
Step 2. Form a vector of parameters
, the components of which are determined on the basis of splines (39) with a nodal points vector
Step 3. Construct natural cubic splines , , with the nodal points vector (14).
Step 4. Form a parameterized program control law
The analysis of the computational experiment results leads to the following main conclusion. If the initial the multicriteria control optimization problem statement is infinite-dimensional, then the use of a transdimensional -search model that implements the search for the optimal control law in space provides a higher efficiency of the optimal program control law compared to finite-dimensional transdimensional search (p/s)-models.
5. Conclusions
A hybrid transdimensional evolutionary algorithm for dynamical system control multicriteria optimization has been developed. The proposed transdimensional search -model is based on the joint use of a finite-dimensional model for the control law parameters global multicriteria optimization and an infinite-dimensional model for the control law local multicriteria optimization.
An evolutionary algorithm of global finite-dimensional multicriteria optimization with respect to the polyhedral dominance cone has been developed. It is shown that the representation of the polyhedral dominance cone as a function of the uncertainty intervals of the vector criterion components weighting coefficients makes it possible to reduce the uncertainty of choice on the set of Pareto optimal solutions. The resulting subset contains solutions that have a higher degree of balance for various components of the vector criterion. This property is achieved by cutting off solutions located on the "edges" of the Pareto set, which often has properties close to the optimal solutions by Slater and a priori do not meet technical requirements.
An algorithm for calculating the polyhedral dominance cone as a function of uncertainty intervals of the vector criterion components weighting coefficients has been developed.
A multicriteria evolutionary algorithm for feasible directions has been developed to solve the problem of the local multicriteria optimization of dynamic systems program control laws. A comparative analysis of transdimensional evolutionary search (p/s)- and -models’ effectiveness is carried out on the example of solving the problem of the optimal law of bioreactor program control multicriteria synthesis. It is shown that the use of a transdimensional search -model that implements the search for the optimal control law in space provides higher efficiency of the optimal law of program control compared with finite-dimensional transdimensional search (p/s)-models.
The general conclusion is that the transdimensional -hybridization of evolutionary algorithms for multicriteria control optimization gives a synergistic effect. This effect is expressed in fundamental increase of the solving accuracy the multicriteria control optimization problem compared to the known hybrid control optimization NIAs by resolving the contradiction between the finite-dimensional global search model and the infinite-dimensional initial problem statement.