Watermark Embedding Scheme with Variance of Chromatic Components ^†

Abstract

This paper contains the idea of inserting a watermark with the variance of color components of the image. The color image is converted into CIE color space. Chromatic components are transformed into a sequency domain by applying the complex Hadamard transform. The variance of the spatio-chromatic coefficients is calculated and the watermark is selected from the transformed image based on the variance by setting the threshold value. The watermark is only inserted in image blocks that have a smaller value of variance than the threshold value. Simulation results are presented and discussed using the two variants of complex Hadamard transform and discrete cosine transform.

1. Introduction

The use of digital material from the internet is modernizing our daily life due to the wide variety of digital systems. A vast amount of information is easily available on the World Wide Web. Therefore, a number of copies of the information can be produced unlawfully, which is a serious crime against the rightful owners. Copyrights provide advantages to the concerned owners to prevent their intellectual work, i.e., audio, video records, photographs, and research papers, from being illegally downloaded and copied. Many researchers are currently working on watermarking techniques. A number of algorithms and methods have been developed for digital image watermarking. Color image watermarking is a challenge due to the perception ability of the human eye [1]. Hidden information is embedded without creating distortions in the host image [2]. Just noticeable difference (JND) is measured on the human visual system (HVS) [3]. Robustness and perceptivity are demanding parameters to forecast the hidden information in the image [4]. Traditionally, watermarking methods are divided into two categories: spatial domain and transform domain [5]. In previous works, the focus was to insert a watermark in the least significant bit of the pixel [6]. Gray image techniques are not robust against the attack; therefore, it is more difficult to tamper with color image watermarking in spatial domains than in transform domains. There are many distinguishing attributes of transform domain schemes. For example, insertion is processed by the transformed coefficients that perceptually cause less deterioration to the watermark by tempering [7]. Up until now, numerous methods have been developed using different transforms, such as discrete Fourier transform (DFT) such as multidirectional vectors. The watermark is embedded as binary data using DFT, which bears the Joint Photographic Experts Group (JPEG) compression [8]. Many algorithms have been developed by using discrete wavelet transform (DWT) [9] and discrete cosine transform (DCT) [10]. Due to its less computational cost and simplicity of the transform, Walsh–Hadamard transform is used in watermarking [11]. Unified complex Hadamard transform (UCHT) [12] is varint of CHT and it is applied for image analysis to hide the information.. On the basis of phase shift keying, the watermark is encoded in the low amplitude blocks using sequency-ordered complex Hadamard transform (SCHT) [13]. Conjugate symmetric SCHT (CS-SCHT) has been applied to image processing [14]. Several approaches have been implemented based on HVS [15] and just noticeable difference (JND) [16,17,18] to achieve challenging factors, such as imperceptivity and robustness. This presents the watermarking technique using the complex Hadamard transform (CHT) using variants SCHT [19] and CS-SCHT [14].

The presented work in this paper is based on watermarking using the coefficients of the transformed image in the sequency domain. The watermark is embedded in sequency vectors to make a more robust insertion of the information. The proposed work is simulated using MATLAB, although it can be performed using R-language and Python. MATLAB is used because image processing applications and algorithms can be easily handled with it.

2. Methods

This algorithm is based on the variance of the chromatic coefficients by ignoring the luminance component in the transform domain. Figure 1 shows the flow diagram for the embedding process. The steps are given below.

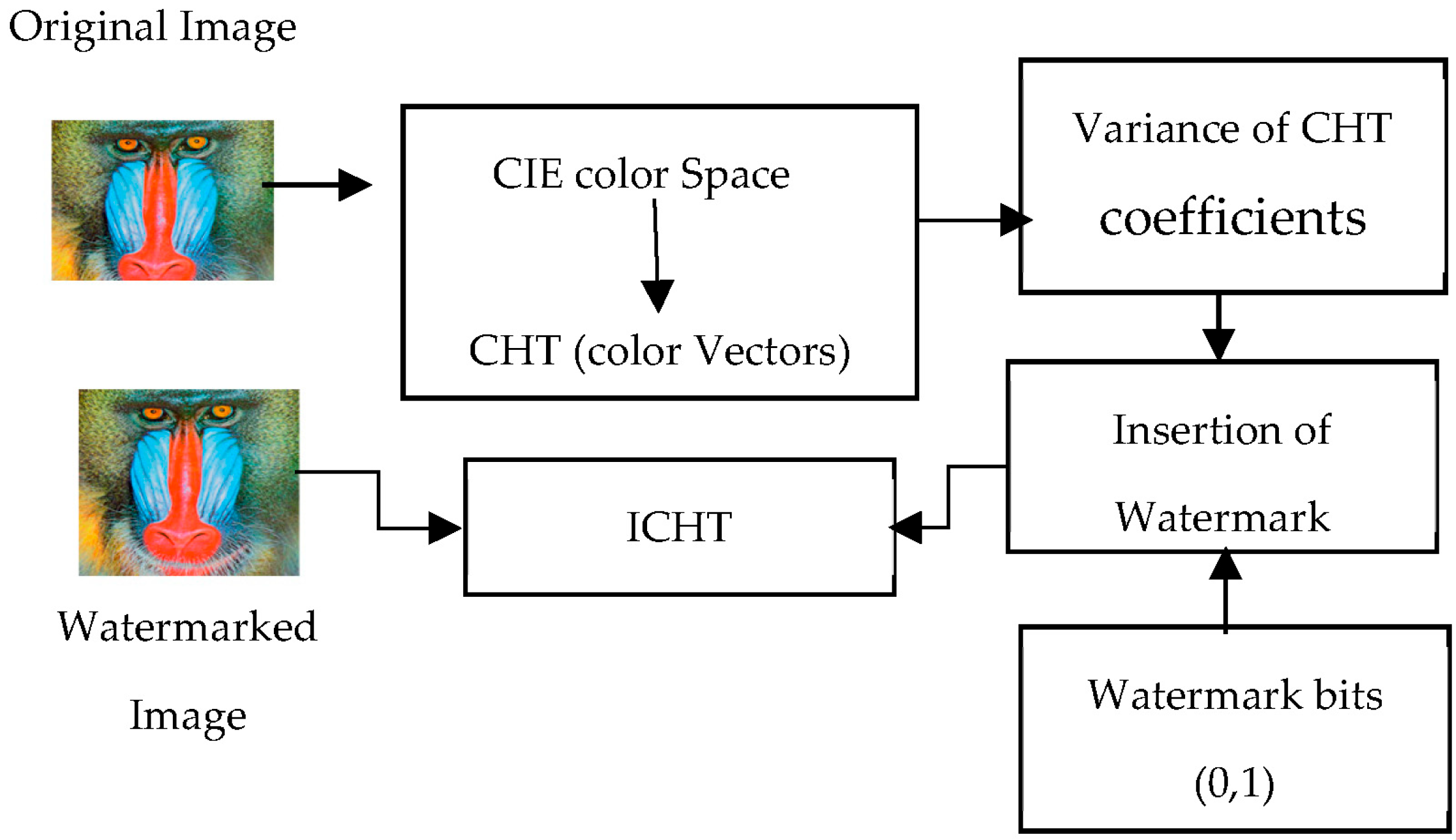
2.1. Steps of the Embedding Scheme

• Converting color images into international commission on illumination (CIE) color spaces, such as Luv and La*b*;
• Dividing images into 8 × 8 blocks;
• Transforming the chromatic components into sequency domain;
• Calculating the variance of the sequency domain coefficients;
• Setting the threshold value for the variance;
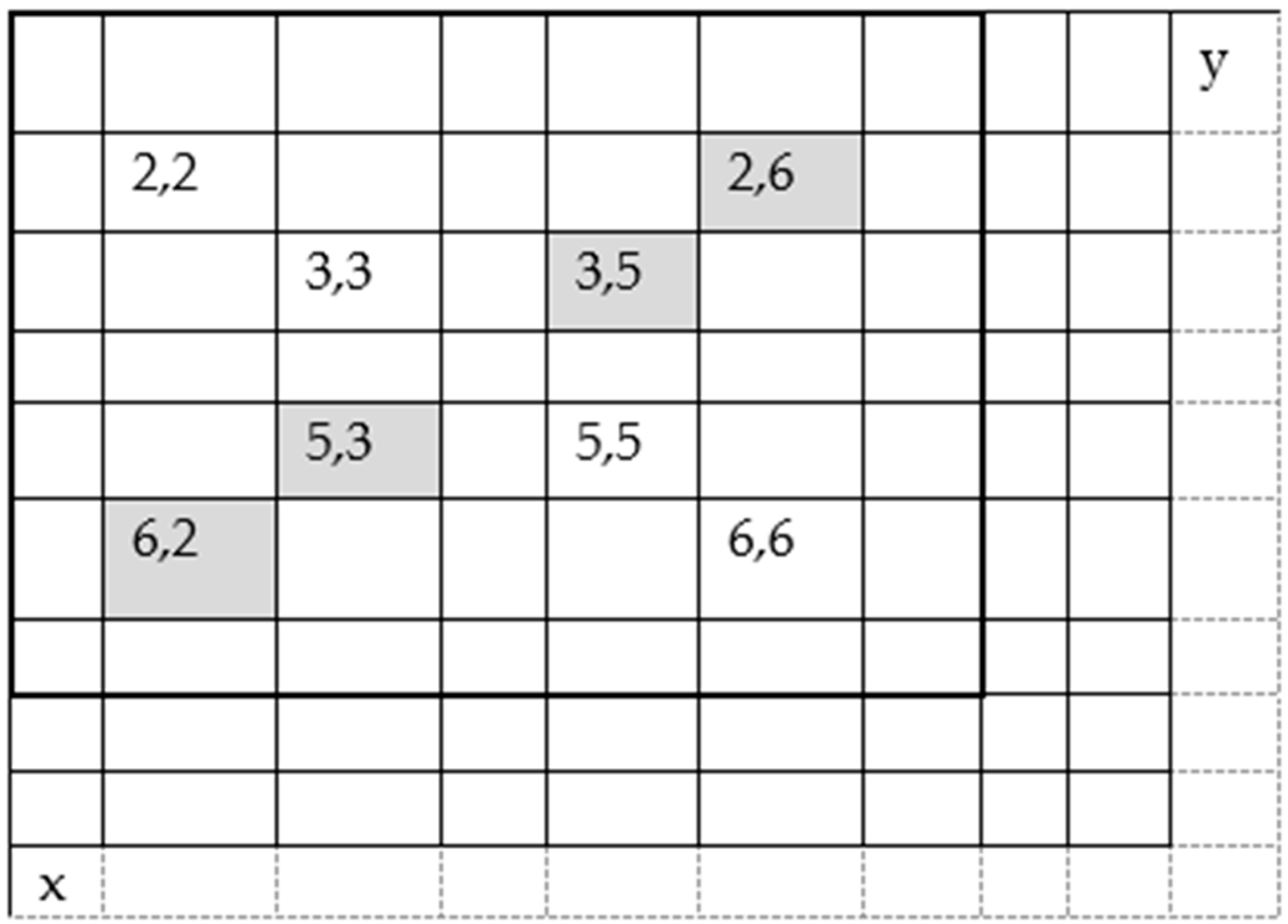
• Selecting the watermark coefficients from the spatio-chromatic coefficients on the bases of variance as shown in Figure 2;
• Generating the watermark bits zero and one;
• Inserting the watermark into the host image according to binary bits and variance;
• Taking inverse transforms of the watermarked image;
• Converting into an RGB image.

2.2. Complex Hadamard Transform

A family of complex Hadamard transform contains discrete and orthogonal transforms [14]. It is a complex modified form of the real Hadamard transform RHT. Transformation matrix values of the CHT variants depend on the unit complex plane $\left\{\pm 1,\pm j\right\}$ [14]. CHT provides the number sequence along the unit complex plane in increasing order of rows/columns of the matrix. The sequence of SCHT and CS-SCHT is more related to the frequency of the most referenced transform DFT, SCHT and CS-SCHT are discussed below.

2.2.1. Sequency-Ordered CHT

SCHT was developed and applied to signal processing and communication system applications. This transform follows sequency ordering. Sequency is a rotation of the row vector across the complex plane at normalized level from $\left(0\to 1\right)$ [13]. The SCHT matrices are discrete transforms that are constrained to four complex values in the unit circle of a complex plane and are orthogonal in the complex domain. In the discrete Fourier transform, sequence is comparable to frequency. SCHT for the two-dimensional signals is as follows:

$$\overline{X}(k_1,k_2)=\frac{1}{\sqrt{N}}{\stackrel{\rightharpoonup }{H}}^{*}\left(\overline{x}(n_1,n_2)\right){({\stackrel{\rightharpoonup }{H}}^T)}^{*}$$

(1)

where, $\stackrel{\rightharpoonup }{H}$ is the SCHT matrix of $N\times N$ size; ${\stackrel{\rightharpoonup }{H}}^{*}$ represents the conjugate of the matrix; and transpose is ${\stackrel{\rightharpoonup }{H}}^T$ [14]. The inverse is as follows:

$$\overline{x}(n_1,n_2)={({\stackrel{\rightharpoonup }{H}}^{*})}^{-1}\left(\overline{X}(k_1,k_2)\right){\left({({\stackrel{\rightharpoonup }{H}}^T)}^{*}\right)}^{-1}$$

(2)

where, $\overline{x}(n_1,n_2)$ is an image; $\overline{X}(k_1,k_2)$ is spectra of the transform domain; and ${\left(\right)}^{-1}$ is the inverse matrix.

2.2.2. Conjugate Symmetric SCHT

CS-SCHT is the conjugate and symmetric form of the SCHT [15]. Its computational cost is less than SCHT due to its conjugate nature, which requires only half of the coefficients for the computational analysis [20]. CS-SCHT was implemented and used in signal processing applications. For two-dimensional signals, CS-SCHT is applied by using the following formula:

$$\overline{X}(k_1,k_2)=\stackrel{⌢}{C}\left(\overline{x}(n_1,n_2)\right){({\stackrel{⌢}{H}}^T)}^{*}$$

(3)

where, $\stackrel{⌢}{H}$ is the CS-SCHT matrix; and $\stackrel{⌢}{C}=\frac{1}{\sqrt{N}}{(\stackrel{⌢}{H})}^{*}$ is the conjugate of CS-SCHT. The inverse of the transform is as follows:

$$\overline{x}(n_1,n_2)={(\stackrel{⌢}{C})}^{-1}\left(\overline{X}(k_1,k_2)\right){\left({({\stackrel{⌢}{H}}^T)}^{*}\right)}^{-1}$$

(4)

3. Embedding Process

After converting the color image into CIE La*b* color space, the sequency domain coefficients are as follows:

$$\overline{X}(k_1,k_2)=A_i(k_1,k_2)+j{B}_i(k_1,k_2)$$

(5)

The watermark is selected on the threshold value ‘z’ if the variance of $\left|A_i(k_1,k_2)+j{B}_i(k_1,k_2)\right|$ is less than and equal to ‘z’, otherwise the watermark coefficient selected will be zero, as shown in Figure 2. The watermark coefficients are selected from each 8 × 8 block of the image, as shown in Figure 3.

If the variance is less than ‘z’ and the secrete bit is high then the watermark is added to the transformed coefficients; otherwise, they are subtracted, as shown below if $\left(V\le z\right)\left(Sb==1\right)$:

$$\overline{X}(k_1,k_2)=A_i(k_1,k_2)+j{B}_i(k_1,k_2)+{\overline{W}}_i(k_1,k_2)$$

(6)

or

$$\overline{X}(k_1,k_2)=A_i(k_1,k_2)+j{B}_i(k_1,k_2)-{\overline{W}}_i(k_1,k_2)$$

(7)

where, ${\overline{W}}_i$ are the watermark coefficients; $V$ is the variance; and $Sb$ is the secrete bit. The original image and the magnified image is given in Figure 4a. The watermarked image is given in Figure 4b,c using SCHT and CS-SCHT, respectively. Secrete bits (Figure 5) are inserted in each block of the image (3, 3 and 5, 5) coefficients. Peak to signal noise ratio (PSNR) is measured at 157.8194 and 156.6337 with processing times 0.693134 and 0.690744 s, respectively, using respective transforms.

4. Decoding Process

For the decoding process, the original images and watermarked images are required. Both of them are transformed into the sequency domain.

$$\overline{D}(k_1,k_2)=\overline{X}(k_1,k_2)-\left(N(k_1,k_2)\right)$$

(8)

5. Discrete Cosine Transform

The most widely used algorithm for digital image and signal processing is the orthogonal transform known as the DCT. The key benefits are a larger compression ratio, lower error ratio, more centralized data capacity, and increased computational complexity issues. Image recovery was accomplished using the inverse DCT procedure. The image is converted into the frequency domain by DCT. Compared to spatial domain techniques, frequency domain techniques are more efficient [21].

• Read the actual image and divide it into 8 by 8 blocks that do not overlap;
• Each non-overlapping block’s forward DCT should be calculated;
• The highest coefficient selection criteria and HVS block selection criteria are applied;
• Add a secret image to the relevant frequency coefficient;
• Each block undergoes an inverse DCT transformation.

6. Result and Discussion

MATLAB is used to accomplish the suggested methods. The PSNR value determined the image quality in digital watermarking. A great-quality image can be found when the PSNR value is between 30 and 50 dB. The results found for SCHT, DCT, and CS-SCHT are listed in

Table 1. PSNR for Unique Transforms.

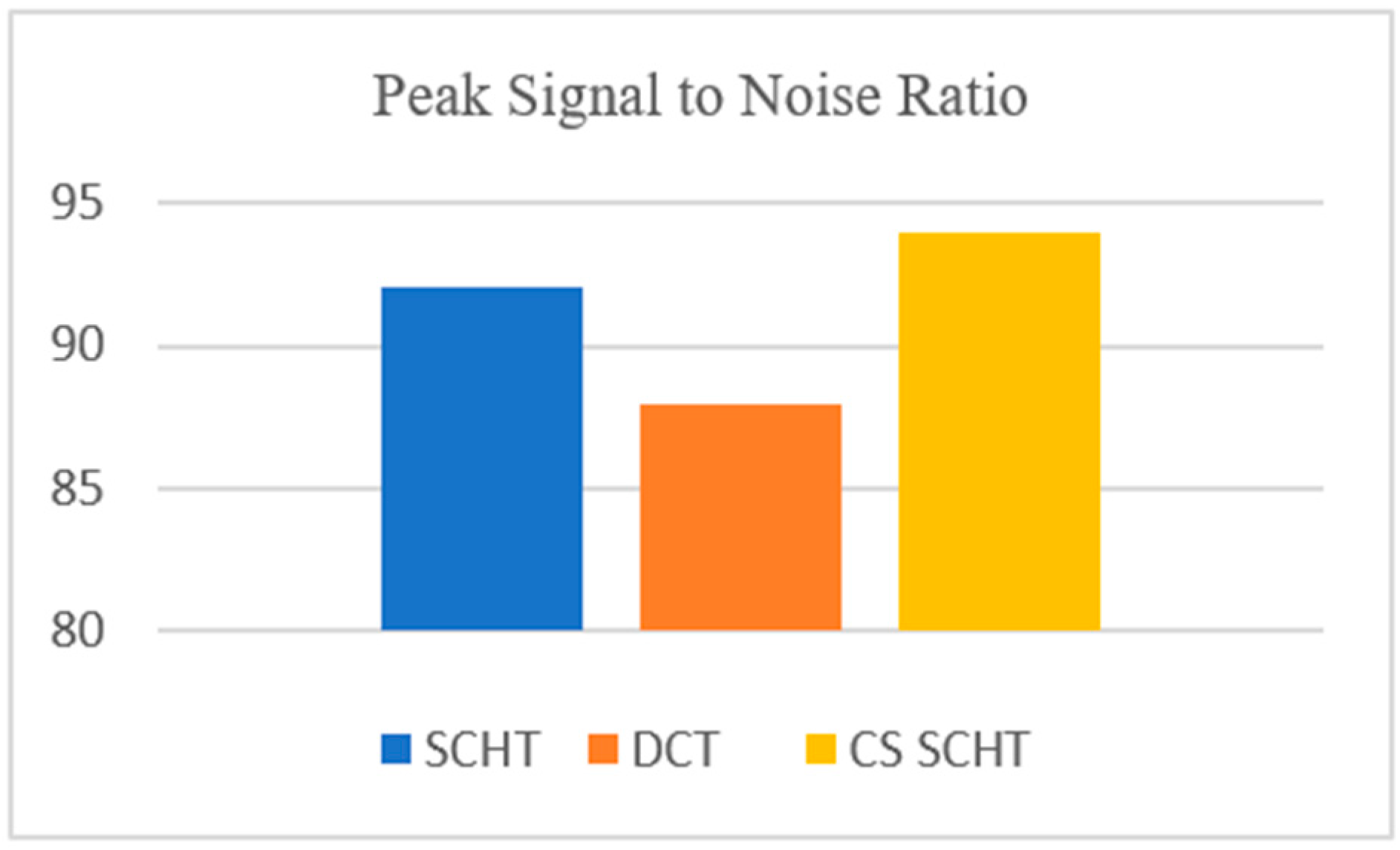
Watermarking Technique	PSNR
CS SCHT	94.0070
SCHT	92.0482
DCT	87.9364

and Figure 6 prested the PSNR compatsion.

It is clear from the table that the conjugate symmetric sequence-ordered complex Hadamard transform’s PSNR value is higher than that of the other approaches, which did not degrade the image’s quality.

7. Conclusions

This paper presents an inventive watermarking method for digital color photographs. The complex Hadamard transform and discrete cosine transform, which is a discrete and orthogonal transform, were used. The two approaches of complex Hadamard have been used, i.e., SCHT and CS-SCHT, to watermark the image. We have also shown that the proposed algorithm is stronger against the most common outbreaks. In addition, when compared to the discrete cosine transform, the approach suggested in this study merely marks the chromatic components by taking the variance of the sequency domain coefficients without adjusting the luminance component. The results obtained were analyzed based on PSNR. The calculated PSNR value proves that watermarking does not affect the quality of the image severely when compared to other prevailing methods. Future work will be devoted to embedding the watermarks into multiple frequency coefficients.