Application of Adaptive Algorithms on Ultrasound Imaging ^†

Abstract

Ultrasound, also known as ultrasonography, plays a major role in the medical imaging field. Ultrasound images are inevitably prone to different kinds of noise and speckle during their acquisition. Adaptive filters show the best performance in removing noise and speckles from images. In this paper, we compared the least mean square algorithm, the quaternion least mean square algorithm, and the normalized least mean square algorithm for ultrasound image processing. It was demonstrated that NLMS displayed the best performance of these algorithms. The results are provided in order to illustrate the performance of algorithms.

1. Introduction

Image processing is a fast-growing technology [1] in various fields across the world, including engineering and medical fields. In the medical field, ultrasound imaging is widely used in clinics and hospitals [2] to diagnose any problem in the specific body part on which the ultrasound is performed. The ultrasound system functions in the frequency range of 3 MHz–30 MHz [3]. According to research, around 12 million people, when seeking medical care, have to suffer due to the wrong diagnosis of their ailment [4]. Ultrasound images are prone to noise, which can lead to the wrong diagnosis and can risk a person’s life. This includes speckle noise, Gaussian noise, salt and pepper noise (impulsive noise), and Poisson noise (shot noise) [5]. Many types of filters have been designed to remove noise from ultrasound images, including median, mean, and Wiener filters, etc. [1]. Mean filters are used to remove speckle noise from images. They select a specific region and calculate its average, and the average value is then replaced by the value of the center pixel [6]. The median filter is a non-linear filter that is used to remove impulsive noise from images [7]. A Wiener filter is an adaptive filter that is used to remove additive noise, e.g., additive white Gaussian noise, from images [3].

Adaptive filters provide a better performance and results when removing noise from images. They provide better image enhancement, image compression, and noise cancellation for 2D signals, i.e., images. Among these, the two dimensional least mean square (2DLMS) [8] algorithm is widely used because of its simplicity, and although it has low computational complexity, the convergence of this algorithm is slow. Therefore, many variants of the least mean square algorithm have been proposed to make convergence faster, e.g., the quaternion least mean square (QLMS) [9] and normalized least mean square (NLMS) [10] algorithms, and to improve its efficiency. In this paper, we used additive white Gaussian noise in ultrasound images and applied these algorithms to remove Gaussian noise from images.

2. Algorithm Used

2.1. LMS Algorithm

In the 2D-LMS algorithm, we use two input images. One is the desired or primary input image, D, and the other is the reference input image or noise, denoted by X. Both the images must be of the same dimension, namely M by M. D and X are correlated with each other. A filter of size of N by N is used, which is convolved with X. The weight update equation of LMS algorithm is given by:

$$\mathrm{W}\mathrm{j}+1(\mathrm{l},\mathrm{k})=\mathrm{W}\mathrm{j}(\mathrm{l},\mathrm{k})+2\times \mathrm{e}\mathrm{j}\times \mathrm{X}(\mathrm{m}-\mathrm{l},\mathrm{n}-\mathrm{k})$$

(1)

where

J = iteration number,

Wj = weight matrix,

$\mathsf{\mu }$ = step size,

X = reference input.

The error in each iteration is calculated by:

$$\mathrm{e}\mathrm{j}=\mathrm{D}\left(\mathrm{m},\mathrm{n}\right)-{\displaystyle {\sum }_{\mathrm{l}=0}^{\mathrm{N}-1}}{\displaystyle {\sum }_{\mathrm{k}=0}^{\mathrm{N}-1}}\mathrm{W}\mathrm{j}\left(\mathrm{l},\mathrm{k}\right)\mathrm{X}\left(\mathrm{m}-\mathrm{l},\mathrm{n}-\mathrm{k}\right)$$

(2)

ej = error signal at jth iteration,

D = primary input,

Wj = weight matrix,

X = reference input.

2.2. QLMS Algorithm

The quaternion least mean square (QLMS) algorithm is an extension of the LMS algorithm, which provides fast convergence by using the concept of the q-derivative. The weight update equation of QLMS algorithm is given as:

$$\mathrm{W}\mathrm{j}+1\left(\mathrm{l},\mathrm{k}\right)=\mathrm{W}\mathrm{j}\left(\mathrm{l},\mathrm{k}\right)+2\left(\mathrm{q}\left(\mathrm{l},\mathrm{k}\right)+1\right)\ast \mathrm{e}\mathrm{j}\ast \mathrm{X}(\mathrm{m}-\mathrm{l},\mathrm{n}-\mathrm{k})$$

(3)

J = number of iterations,

Wj = weight matrix,

$\mathsf{\mu }$ = step size,

X = reference input.

The error in each iteration is calculated by:

$$\mathrm{e}\mathrm{j}=\mathrm{D}\left(\mathrm{m},\mathrm{n}\right)-{\sum }_{\mathrm{l}=0}^{\mathrm{N}-1}{\sum }_{\mathrm{k}=0}^{\mathrm{N}-1}\mathrm{W}\mathrm{j}(\mathrm{l},\mathrm{k})\mathrm{X}(\mathrm{m}-\mathrm{l},\mathrm{n}-\mathrm{k})$$

(4)

ej = error signal at jth iteration,

D = primary input,

Wj = weight matrix,

X = reference input.

2.3. NLMS Algorithm

Another extension of the LMS algorithm is the normalized least mean square (NLMS) algorithm that calculates the step size at each iteration to achieve a faster convergence. The weight update equation of NLMS algorithm is given as:

$$\mathrm{W}\mathrm{j}+1\left(\mathrm{l},\mathrm{k}\right)=\mathrm{W}\mathrm{j}\left(\mathrm{l},\mathrm{k}\right)+2\mathsf{\mu }\left(\mathrm{n}\right)\ast \mathrm{e}\mathrm{j}\ast \mathrm{X}(\mathrm{m}-\mathrm{l},\mathrm{n}-\mathrm{k})$$

(5)

J = number of iteration,

Wj = weight matrix,

$\mathsf{\mu }$ = step size,

X = reference input.

The step size in each iteration is calculated by:

$$\mathsf{\mu }\left(\mathrm{n}\right)=\frac{\mathsf{\alpha }}{\mathrm{C}+x^T\left(\mathrm{m},\mathrm{n}\right)\mathrm{x}(\mathrm{m},\mathrm{n})}$$

(6)

where

$\mathsf{\alpha }$ = constant (0 < $\mathsf{\alpha }$ < 2),

C = constant (less than 1),

x(m,n) = reference input.

The error in each iteration is calculated by:

$$\mathrm{e}\mathrm{j}=\mathrm{D}\left(\mathrm{m},\mathrm{n}\right)-{\sum }_{\mathrm{l}=0}^{\mathrm{N}-1}{\sum }_{\mathrm{k}=0}^{\mathrm{N}-1}\mathrm{W}\mathrm{j}(\mathrm{l},\mathrm{k})\mathrm{X}(\mathrm{m}-\mathrm{l},\mathrm{n}-\mathrm{k})$$

(7)

ej = error signal at jth iteration,

D = primary input,

Wj = weight matrix,

X = reference input.

3. Results and Discussion

The algorithms were applied to images of a thyroid, a mass in muscle, and a thyroid cyst. Additive white Gaussian noise was first added to the images, and then the algorithms were applied. The results are shown in Figure 1, Figure 2 and Figure 3.

3.1. PSNR Values

Table 1. PSNR values of the applied algorithms.

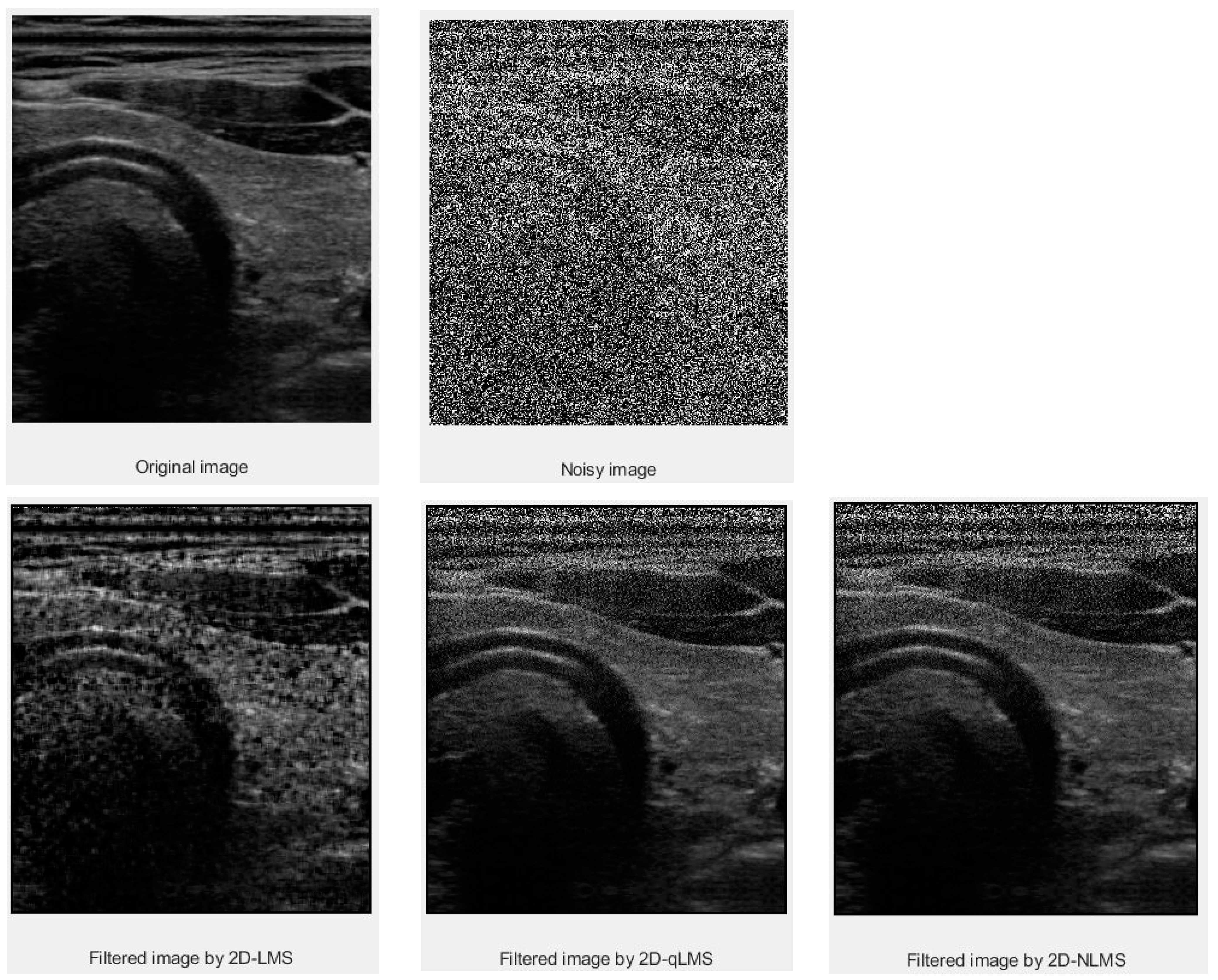
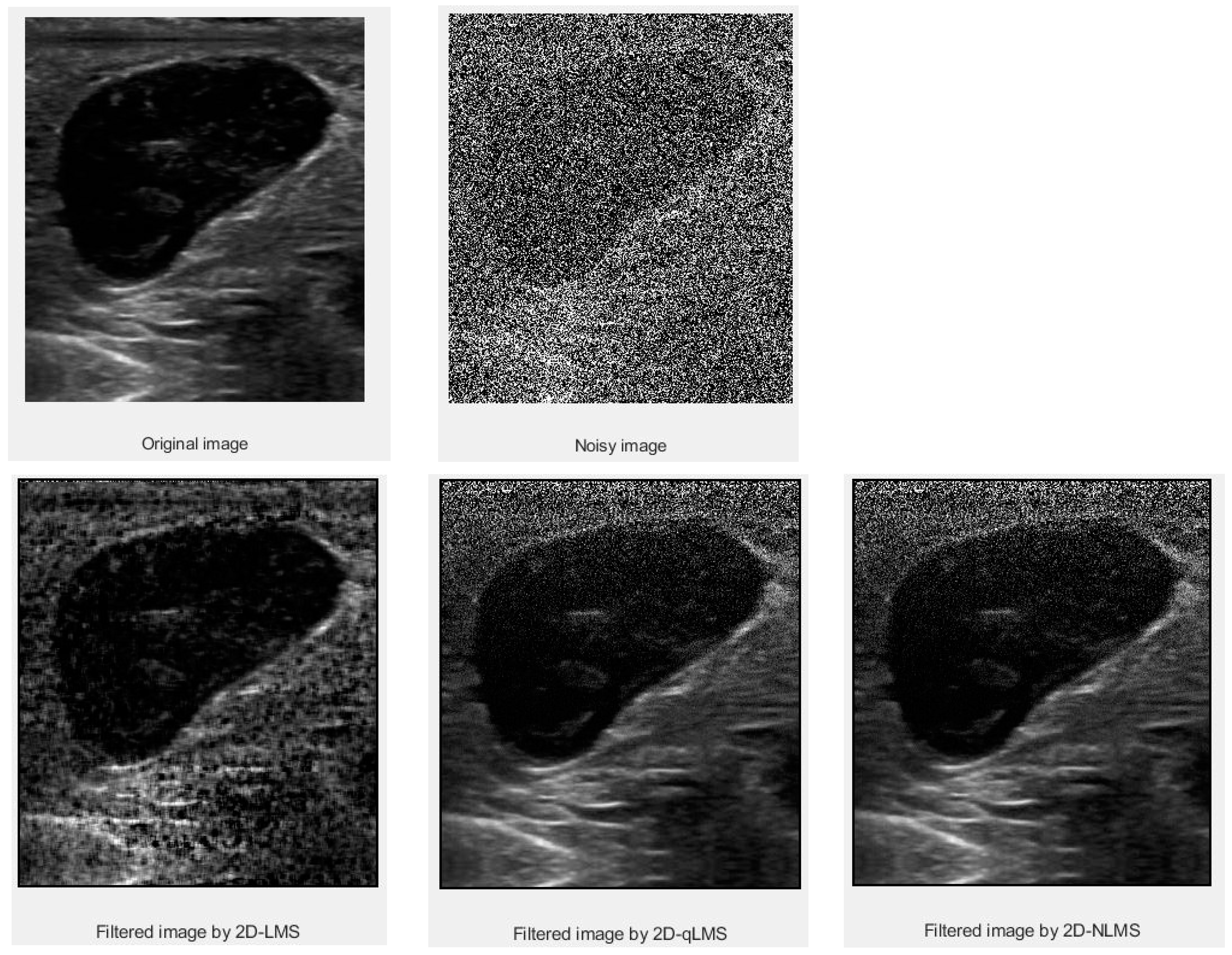
Data	Filter Size	LMS	QLMS	NLMS
Thyroid	5 × 5	64.0167	70.0593	72.8341
Thyroid Cyst	5 × 5	64.0506	69.1289	72.8708
Mass in Muscle	5 × 5	63.8117	69.1211	72.2958

shows the peak signal-to-noise ratio (PSNR) values of the applied algorithms.

3.2. SSIM Values

Table 2. SSIM values of the applied algorithms.

Data	Filter Size	LMS	QLMS	NLMS
Thyroid	5 × 5	0.9996	0.9997	0.9998
Thyroid Cyst	5 × 5	0.9993	0.9997	0.9999
Mass in Muscle	5 × 5	0.9996	0.9998	0.9999

shows the structural similarity index measurement (SSIM) values of the applied algorithms.

4. Conclusions

The least mean square (LMS), quaternion least mean square (QLMS), and normalized least mean square (NLMS) algorithms were applied to different ultrasound images. This paper proves that of these algorithms tested on ultrasound images for noise reduction, the normalized least mean square (NLMS) algorithm gave better results than the others. This can also clearly be seen in the data given in the tables above, as well as in the ultrasound images on which the algorithms were tested. Following NLMS, QLMS is the second best algorithm for the cancellation of additive white Gaussian noise.

As stated in the conclusions above, NLMS is the best of the algorithms tested. Additionally, as we already know that QLMS functions better than LMS, we concluded that inducing the q-factor into the NLMS algorithm would result in a better algorithm proposition for image processing in ultrasound.

5. Future Work

In the future, we plan on inducing the Q-factor in the NLMS algorithm, and we also plan on designing a new algorithm for noise cancellation in ultrasound imaging, which works better than all the algorithms analyzed in this paper. We also plan on taking the direct data of ultrasound images by a transducer and applying our proposed algorithm directly to it, rather than only utilizing database images.