Nonlinear Filter for a System with Randomly Delayed Measurements and Inputs ^†

Abstract

This paper deals with a remote state estimation problem for a nonlinear system. In a typical networked control system (NCS) scenario, the estimator and controller are remotely located, and they are connected with the plant through a common communication network. Traditional Bayesian filters assume that the measurements are always available. However, this may not be the case in reality. As the sensor measurements are transmitted to the remotely located estimator through an unreliable communication channel, delay may arise during data transfer. Similarly, the control signal is also applied remotely, and it reaches to the plant through a similar unreliable communication channel, and due to which here also delay may occur. In this paper, the authors develop a generalized framework of nonlinear filtering where the states can be estimated in the presence of arbitrary random delay in (i) transmission of measurement from sensor to the estimator and (ii) transmission of input from the remotely located controller to the system. The filtering algorithm in such a scenario is realized with deterministic sample points. The performance of the proposed method is tested experimentally on one simulation problem. With the help of the simulation result, it is shown that the developed method performs better than traditional non-delayed nonlinear filters in the presence of arbitrary delay in measurement and input.

1. Introduction

In the networked control system (NCS) [1,2], traditional Bayesian filters assumed that measurements are always available and reach to estimator without delay. However, that may not be the case in reality. In such a scenario [2], the estimator and controller are remotely located, and they are connected with the physical system through a common network. Here, the sensor measurements reach the remotely located estimators through a common network, which incurs delay in it. Similarly, the input signal is applied remotely, and it reaches to plant through a common network.

In this paper, the emphasis is given to handle measurement delay that arises due to the transmission of measurement signals through a common network channel. The literature on the described problem began with the work of Ray et al. [3], where the authors developed a randomly delayed filtering method for linear systems [4]. In [5], an optimal filter is proposed for randomly sampled and delayed measurements. Later, Sun et al. [6] have introduced an optimal filtering algorithm considering packet dropouts and extended their work [7] for randomly delayed measurements and inputs. Hermoso-Carazo et al. considered a nonlinear system and proposed a suboptimal solution with the extended Kalman filter (EKF) [8] and unscented Kalman filter (UKF) [9] for one step [10], and two steps [11] randomly delayed measurements. Wang et al. have used the cubature Kalman filter (CKF) [12] for one step randomly delayed measurement [13]. Zhang et al. [14] have proposed a new particle filter algorithm [15] when model parameter for delay in the channel (latency probability) is unknown. All the above filters assume that the random delay’s extent is known. Singh et al. [16] introduced a framework of Bayesian filtering for a nonlinear system where the delay could be arbitrary and random. Under this framework, the cubature quadrature Kalman filter (CQKF) [16,17], UKF [18] and particle filter [19] were realized.

To date, no estimator has been formulated for nonlinear systems that can take care of the effect of input, applied remotely, and transmitted the system through an unreliable communication channel. In this paper, we extend the work of [16], so that a generalized framework of nonlinear filtering could be developed which can estimate the states in the presence of arbitrary random delay during (i) transmission of measurement to estimator, and (ii) transmission of input from the controller (located remotely) to system. It is seen that to realize any filter in the proposed framework, a few intractable integrals are required to be evaluated. We have used the cubature quadrature rule of integration [17] to realize those integrals. The developed method is named as randomly delayed cubature quadrature Kalman filter (CQKF-RD), and it is applied to one nonlinear estimation problem. The simulation result shows that the developed CQKF-RD outperforms ordinary CQKF in the presence of randomly delayed measurement and input.

2. Problem Formulation

Let us consider a dynamic system whose state equation is given by

$$x_k=\varphi \left(x_{k-1}\right)+B{\tilde{u}}_k+{\eta }_{k-1},$$

(1)

and measurement equation is

$$z_k=\gamma \left(x_k\right)+{\nu }_k,$$

(2)

where $x_k\in {\mathbb{R}}^n$ is a state vector and $z_k\in {\mathbb{R}}^d$ is sensor measurement. $\varphi \left(x_k\right)\in {\mathbb{R}}^n$ and $\gamma \left(x_k\right)\in {\mathbb{R}}^d$ are nonlinear function of $x_k$. B is a matrix with acceptable dimension, and ${\tilde{u}}_k$ is the control input received by the system. ${\eta }_k\in {\mathbb{R}}^n$ is the process noise, and ${\nu }_k\in {\mathbb{R}}^d$ is the measurement noise. ${\eta }_k$ and ${\nu }_k$ are assumed to be white, mutually uncorrelated and normally distributed with zero mean and covariance $Q_k$, $R_k$, respectively.

2.1. Delayed Measurement

In NCS, sensor measurements $\left(z_k\right)$ reach the remote estimator through a common, unreliable communication network. Due to limited bandwidth and common network channels, data may be delayed. Moreover, the delay may be a random and arbitrary step. The delayed measurement $\left(y_k\right)$ can be expressed as

$$y_k=\sum _{i=0}^{N-1}{\beta }^{(j,i)}{z}_{k-i},$$

(3)

where ${\beta }^{(j,i)}=\left({\prod }_{j=0}^i{\beta }_j\right)(1-{\beta }_{i+1})$, ${\beta }_j$ ( $j=0,1,2,\cdots$) are mutually independent Bernoulli random variables and the value of ${\beta }_0$ is 1. As ${\beta }_j$ is the Bernoulli random variable, the values of ${\beta }_j$ could be either 0 or 1. $N-1$ is considered as the maximum extent of delayed step. From Equation (3), we see that at any instant at most one ${\beta }^{(j,i)}$ will be 1 and all other ${\beta }^{(j,i)}$ will be 0. When ${\beta }^{(j,i)}$ will be 1, we will get $i^{th}$ step delayed measurement.

Furthermore, the variable ${\beta }_j$ satisfies $P({\beta }_j=1)=p_j$ and $P({\beta }_j=0)=1-p_j$, where $p_j$ is latency probability. From the distribution of ${\beta }_j$, it can be easily obtained that $E\left[{\beta }_j\right]=p_j$ and $E\left[{\beta }_j^2\right]=p_j$.

2.2. Delay in Control Input

Here, $u_k$ is the control input, determined in the remote location. It is transmitted to the plant through an unreliable network. The control input received by the plant (${\tilde{u}}_k$) can be expressed as

$${\tilde{u}}_k=\sum _{i=0}^{N-1}{\alpha }^{(j,i)}{u}_{k-i},$$

(4)

where ${\alpha }^{(j,i)}=\left({\prod }_{j=0}^i{\alpha }_j\right)(1-{\alpha }_{i+1})$, ${\alpha }_j,j\in \{0,1,2,\cdots \}$ are mutually independent Bernoulli random variables and the value of ${\alpha }_0$ is 1. Moreover, $P({\alpha }_j=1)=q_j$ and $P({\alpha }_j=0)=1-q_j$, where $q_j$ is latency probability. From the distribution of ${\alpha }_j$, we can calculate that $E\left[{\alpha }_j\right]=q_j$ and $E\left[{\alpha }_j^2\right]=q_j$.

3. Bayesian Estimation for Randomly Delayed Measurements and Inputs

In this section, we derive a few Lemmas, which will be used to construct the nonlinear filtering algorithm for the considered scenario. It is to be noted that, due to nonlinearity in process and measurement model, the prior and posterior probability density function (pdf) of states will be non-Gaussian and arbitrary. Throughout the derivation, we assume that the prior and posterior pdf of states are Gaussian and characterized with mean and covariance. In filtering literature, the estimators designed with this assumption are collectively known as Gaussian filter [9,12,17].

Assumption 1.

We assume that there is no loss of control and measurement data during transmission. They are only delayed by maximum $(N-1)$ step. This is a prerequisite of all the remaining Lemmas.

Lemma 1.

The expectation of control input received to the plant is given by $E\left[{\tilde{u}}_k\right]={\sum }_{i=0}^{N-1}\left({\prod }_{j=1}^i{q}_j\right)(1-q_{i+1})u_{k-i}$.

Proof. 

From Equation (4), it can be written as

$$E\left[{\tilde{u}}_k\right]=E\left[\sum _{i=0}^{N-1}{\alpha }^{(j,i)}{u}_{k-i}\right]=\sum _{i=0}^{N-1}E\left[{\alpha }^{(j,i)}\right]E\left[u_{k-i}\right].$$

(5)

Substituting the value of $E\left[{\alpha }^{(j,i)}\right]$ which can be calculated similarly to $E\left[{\beta }^{(j,i)}\right]$ in [16], we obtain

$$E\left[{\tilde{u}}_k\right]=E\left[\sum _{i=0}^{N-1}{\alpha }^{(j,i)}{u}_{k-i}\right]=\sum _{i=0}^{N-1}\left(\prod _{j=1}^i{q}_j\right)(1-q_{i+1})u_{k-i}.$$

(6)

□

Lemma 2.

The expectation of ${\tilde{u}}_k{\tilde{u}}_k^T$ can be expressed as $E\left[{\tilde{u}}_k{\tilde{u}}_k^T\right]={\sum }_{i=0}^{N-1}\left({\prod }_{j=1}^i{q}_j^2\right){(1-q_{i+1})}^2{u}_{k-i}{u}_{k-i}^T$.

The derivation of Lemma 2 is similar to Lemma 1, and proof is not provided here due to page restriction. Generally, Bayesian filters are realized in two steps: (i) time update (ii) measurement update.

3.1. Time Update

In this step, we calculate prior mean (${\widehat{x}}_{k|k-1}$) and prior error covariance ($P_{k|k-1}$). The expressions for them are derived in Lemmas 3 and 4.

Lemma 3.

Prior estimate of the states can be expressed as ${\widehat{x}}_{k|k-1}=\int \varphi \left(x_{k-1}\right)\mathcal{N}(x_{k-1};{\widehat{x}}_{k-1|k-1},P_{k-1|k-1})d{x}_{k-1}+BE\left[{\tilde{u}}_k\right]$.

Proof. 

Prior mean,

$$\begin{array}{cc}\hfill {\widehat{x}}_{k|k-1}& =E\left[x_k\right|y_{1:k-1}]\hfill \\ & =E\left[(\varphi \left(x_{k-1}\right)+B{\tilde{u}}_k+{\eta }_{k-1})\right|y_{1:k-1}]\hfill \\ & =\int \varphi \left(x_{k-1}\right)\mathcal{N}(x_{k-1};{\widehat{x}}_{k-1|k-1},P_{k-1|k-1})d{x}_{k-1}+BE\left[{\tilde{u}}_k\right].\hfill \end{array}$$

□

In the above equation, $E\left[{\tilde{u}}_k\right]$ can be calculated using Lemma 1.

Lemma 4.

Prior error covariance can be expressed as $P_{k|k-1}=E\left[\varphi \left(x_{k-1}\right){\varphi }^T\left(x_{k-1}\right)\right|y_{1:k-1}]-E\left[\varphi \left(x_{k-1}\right)\right|y_{1:k-1}]E\left[{\varphi }^T\left(x_{k-1}\right)\right|y_{1:k-1}]+Q_k+BE\left[{\tilde{u}}_k{\tilde{u}}_k^T\right]B^T-BE\left[{\tilde{u}}_k\right]E\left[{\tilde{u}}_k^T\right]B^T.$

Proof. 

Prior estimate error can be written as

$$\begin{array}{cc}\hfill e_{k|k-1}& =x_k-{\widehat{x}}_{k|k-1}\hfill \\ & =\varphi \left(x_{k-1}\right)+B({\tilde{u}}_k-E\left[{\tilde{u}}_k\right])+{\eta }_{k-1}-E\left[\varphi \left(x_{k-1}\right)\right|y_{1:k-1}],\hfill \end{array}$$

where $B^{\prime }=B({\tilde{u}}_k-E\left[{\tilde{u}}_k\right])$ and $E\left[B^{\prime }\right]=E\left[B({\tilde{u}}_k-E\left[{\tilde{u}}_k\right])\right]=0$. Prior error covariance can be expressed as

$$\begin{array}{cc}\hfill P_{k|k-1}& =E\left[e_{k|k-1}{e}_{k|k-1}^T\right|y_{1:k-1}]\hfill \\ & =E\left[\{\varphi \left(x_{k-1}\right)+B^{\prime }+{\eta }_{k-1}-E\left[\varphi \left(x_{k-1}\right)\right|y_{1:k-1}]\}{\{\varphi \left(x_{k-1}\right)+B^{\prime }+{\eta }_{k-1}-E\left[\varphi \left(x_{k-1}\right)\right|y_{1:k-1}]\}}^T\right|y_{1:k-1}]\hfill \\ & =E\left[\right\{\varphi \left(x_{k-1}\right){\varphi }^T\left(x_{k-1}\right)-\varphi \left(x_{k-1}\right)E\left[{\varphi }^T\left(x_{k-1}\right)\right|y_{1:k-1}]+B^{\prime }{B}^{\prime T}+{\eta }_{k-1}{\eta }_{k-1}^T-E\left[\varphi \left(x_{k-1}\right)\right|y_{1:k-1}]{\varphi }^T\left(x_{k-1}\right)\hfill \\ & +E\left[\varphi \left(x_{k-1}\right)\right|y_{1:k-1}]E\left[{\varphi }^T\left(x_{k-1}\right)\right|y_{1:k-1}]\left\}\right|y_{1:k-1}]+C,\hfill \end{array}$$

where $C=E\left[\{\varphi \left(x_{k-1}\right){B^{\prime }}^T+\varphi \left(x_{k-1}\right){\eta }_{k-1}^T+B^{\prime }{\varphi }^T\left(x_{k-1}\right)+B^{\prime }{\eta }_{k-1}^T-B^{\prime }E\left[{\varphi }^T\left(x_{k-1}\right)\right|y_{1:k-1}]+{\eta }_{k-1}{\varphi }^T\left(x_{k-1}\right)-{\eta }_{k-1}E\left[{\varphi }^T\left(x_{k-1}\right)\right|y_{1:k-1}]+{\eta }_{k-1}{B}^{\prime T}-E\left[\varphi \left(x_{k-1}\right)\right|y_{1:k-1}]B^{\prime T}-E\left[\varphi \left(x_{k-1}\right)\right|y_{1:k-1}]{\eta }_{k-1}^T\}\right|y_{1:k-1}]$.

As $E\left[{\eta }_k\right]=0$ and $E\left[B^{\prime }\right]=0$, $C=0$. Finally, the prior error covariance can be written as

$$\begin{array}{cc}\hfill P_{k|k-1}& =E\left[\varphi \left(x_{k-1}\right){\varphi }^T\left(x_{k-1}\right)\right|y_{1:k-1}]-E\left[\varphi \left(x_{k-1}\right)\right|y_{1:k-1}]E\left[{\varphi }^T\left(x_{k-1}\right)\right|y_{1:k-1}]+BE\left[{\tilde{u}}_k{\tilde{u}}_k^T\right]B^T-BE\left[{\tilde{u}}_k\right]\hfill \\ & E\left[{\tilde{u}}_k^T\right]B^T+Q_k.\hfill \end{array}$$

(7)

□

In the above equation, $E\left[{\tilde{u}}_k\right]$ and $E\left[{\tilde{u}}_k{\tilde{u}}_k^T\right]$ can be calculated with the help of Lemmas 1 and 2, respectively.

3.2. Measurement Update

In this step, the prior pdf is combined with the current measurement and provides the refined state estimate, generally called the posterior state estimate. To compute the posterior state estimate, ${\widehat{x}}_{k|k}$ and error covariance ($P_{k|k}$), we need to evaluate the estimated value of delayed measurement ${\widehat{y}}_{k|k-1}$, covariance of the delayed measurement $P_{k|k-1}^{yy}$, and cross-covariance between state and delayed measurement $P_{k|k-1}^{xy}$. The detailed derivation of these equations is given in [16], and readers are requested to see those equations.

Finally, we calculate the posterior state estimate and error covariance matrix as follows:

$${\widehat{x}}_{k|k}={\widehat{x}}_{k|k-1}+K(y_k-{\widehat{y}}_{k|k-1}),$$

(8)

$$P_{k|k}=P_{k|k-1}-K{P}_{k|k-1}^{yy}{K}^T,$$

(9)

where the Kalman gain, K is

$$K=P_{k|k-1}^{xy}{\left(P_{k|k-1}^{yy}\right)}^{-1}.$$

(10)

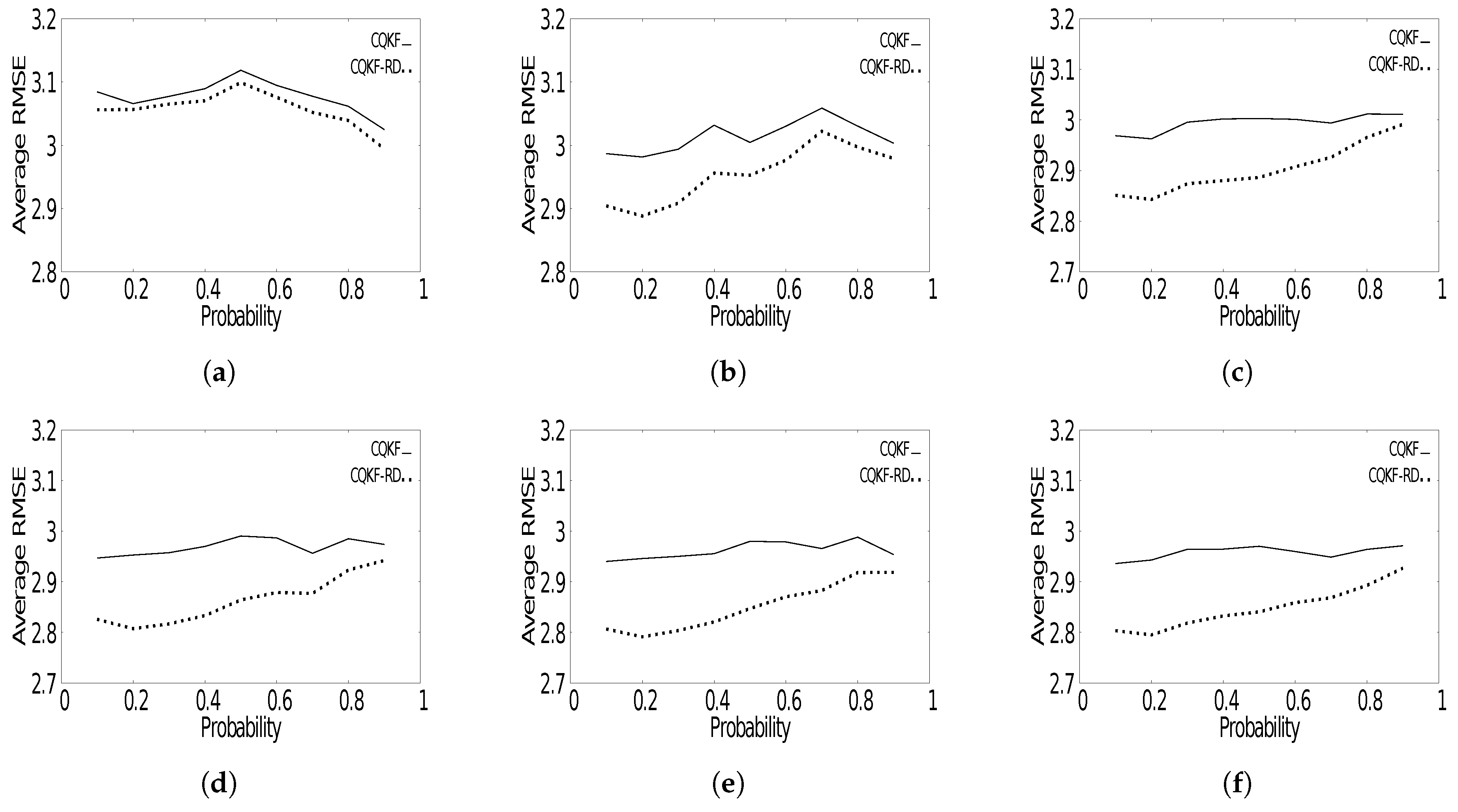
4. Simulation Result

Problem 1: In this problem, we consider a nonlinear system [16], with process model

$$x_k=2cos\left(x_{k-1}\right)+B{\tilde{u}}_k+{\eta }_k,$$

and measurement model

$$y_k=\sqrt{1+x_k^T{x}_k}+{\nu }_k,$$

where $x_k\in {\mathbb{R}}^6$ is the state vector, $y_k\in \mathbb{R}$ is the measurement and $u_k$ is control input. The process noise, ${\eta }_k$, and measurement noise, ${\nu }_k$, are assumed to be uncorrelated, white and normally distributed with mean zero, and covariance $Q_k$ and $R_k$, respectively. For this problem, the following values are used for simulation: $u_k$=2$sin\left(0.2k\right)$, $Q_k$=$5I_n$ and $R_k$=5. Initial truth value of the state is $x_0$=$0.1_{6\times 1}$. The filter is initialized with ${\widehat{x}}_{0|0}$=${15}_{6\times 1}$ and $P_{0|0}$=5$I_6$.

Simulation has been carried out for 200 time-steps. Here, second order quadrature $(n^{\prime }=2)$ is used for CQKF and CQKF-RD. Filtering performance has been compared in terms of averaged root mean square error (RMSE) calculated over 200 Monte Carlo runs for different values of p (we assume $p=q$) and plotted in Figure 1. From the figure, we see that the proposed filter performs better than conventional CQKF.

5. Discussion and Conclusions

In a cyber physical system, it is very common that an estimator and controller are remotely located, and communicate with the plant through a common unreliable network. During such communications, data may be delayed randomly. In this paper, we have developed a framework for nonlinear filtering where the measurements and input data are randomly delayed. The framework is realized with a popular Gaussian filter, namely CQKF. With the help of one nonlinear filtering problem, the superiority of the proposed method over the traditional filter has been demonstrated.