Abstract
In today’s data-driven world, time series forecasting is an intensively investigated temporal data mining technique. In practice, there is a range of forecasting techniques that have been proven to be efficient at capturing different aspects of an input. For instance, classic linear forecasting models such as seasonal autoregressive integrated moving average (S-ARIMA) models are known to capture the trends and seasonality evident in temporal datasets. In contrast, neural-network-based forecasting approaches are known to be best at capturing nonlinearity. Despite such differences, most forecasting techniques inherently assume that models are fitted using a single input. In practice, there are often cases where we cannot deploy forecasting models in this manner. For instance, in most wireless communication traffic forecasting problems, temporal datasets are defined by taking samples from hundreds of base stations. Moreover, the base stations are expected to have spatial correlation due to user mobility, land use, settlement patterns, etc. Thus, in such cases, it is often advised that forecasting should be approached using clusters that group the base stations based on their traffic patterns. However, when this approach is used, the quality of the cluster centroids and the overall cluster formation process is expected to have a significant impact on the performance of forecasting models. In this paper, we show the effectiveness of representation learning for cluster formation and cluster centroid definition, which in turn improves the quality of cluster-level forecasting. We demonstrate this concept using data traffics collected from 729 wireless base stations. In general, based on the experimental results, the representation learning approach outperforms cluster-level forecasting models based on classical clustering techniques such as K-means and dynamic time warping barycenter averaging K-means (DBA K-means).
1. Introduction
Time series forecasting (prediction) is a well-developed temporal data mining technique [1,2,3,4]. The theory of time series forecasting often relies on the data having recognizable patterns that can either be captured or learned. In practice, patterns or components within a time series dataset include trends, seasonality, cycles, and irregular (error) components [2,5,6]. In general, given a set of time series denoted by , the forecasting task can be formalized as:
where, is the forecast for the ith series for p forward steps or horizons. Moreover, are past observations over a look-back window L. In most practical cases, different forecasting techniques often aim to provide predictions for a range of future time stamps [1,2,5]. However, when this is the case, it is important to carefully address the propagation of errors and the size of the look-back window. In this regard, some forecasting techniques often incorporate exogenous variables that are presumed to add value to (improve) the prediction accuracy [6]. In Equation (1), the possibility of incorporating exogenous variables is indicated using the parameter . In practice, we can broadly categorize forecasting models based on different factors. For instance, we can categorize them into univariate or multivariate models based on their ability to incorporate either a single or multiple time series. We can also categorize them, based on their mathematical formulation, as linear or nonlinear [1]. In general, on deployment, the underlying data often govern which of the different forecasting models is to be utilized. For instance, if forecasting is performed on a group of input time series that have some degree of correlation, then multivariate techniques are more fitting [6,7,8]. In contrast, if forecasting is performed on a group of series that show a sense of independence, standard univariate techniques are often considered [9].
In practice, despite the differences among forecasting approaches, we must overcome certain challenges and limitations that are associated with either the underlying data or a forecasting model [1]. For instance, a limited number of training samples often leads to the overfitting problem. In reality, overfitting is a problem in both univariate and multivariate forecasting approaches [2,5,10]. However, in reality, there are also challenges (limitations) that are specific to a given forecasting approach. For example, in some practical cases, univariate forecasting models often fail to capture the dynamic nature of the underlying data [3,11]. This is because, in these approaches, the model’s locality with respect to an individual time series will restrict its scalability in the context of other correlated time series [5,7]. For instance, in most wireless communication forecasting problems, temporal datasets are collected from a range of base stations that share a certain geographical area [6,11]. In these cases, deploying univariate forecasting models on an individual base station is often not advised for two reasons [3,11]. Firstly, due to the presence of user mobility, settlement patterns, land use, etc., base stations cannot be treated as isolated entities. Consequently, a given base station is expected to have a piece of inherent hidden information about its neighbors [12,13]. In addition to this, in wireless communication networks, the base stations number hundreds if not thousands. Therefore, the sheer number alone makes it challenging to deploy univariate forecasting models. In order to overcome these and other additional challenges, most univariate time series forecasting tasks make use of pre-processing techniques. For instance, prior to fitting most univariate linear forecasting models, an input series is often processed in the context of identifying seasonal patterns, extracting external explanatory variables, putting a limit on the forecasting horizon, and using a “global” approach, which clusters the time series based on similarity [1,2,5,6,11,14]. Among such pre-processing steps, clustering is often considered to be useful in capturing the spatial correlations and reducing the number of required forecasting models [11,14]. This is because, while clustering, we often group base stations that have similar traffic patterns around a centroid (average). Thus, given an optimal cluster centroid, the patterns observed within cluster members can be generalized. This, in turn, provides a way to embed the information a base station has about its neighbors. Moreover, it has been shown to be possible to further incorporate spatial correlation by defining a cluster correlation matrix [11].
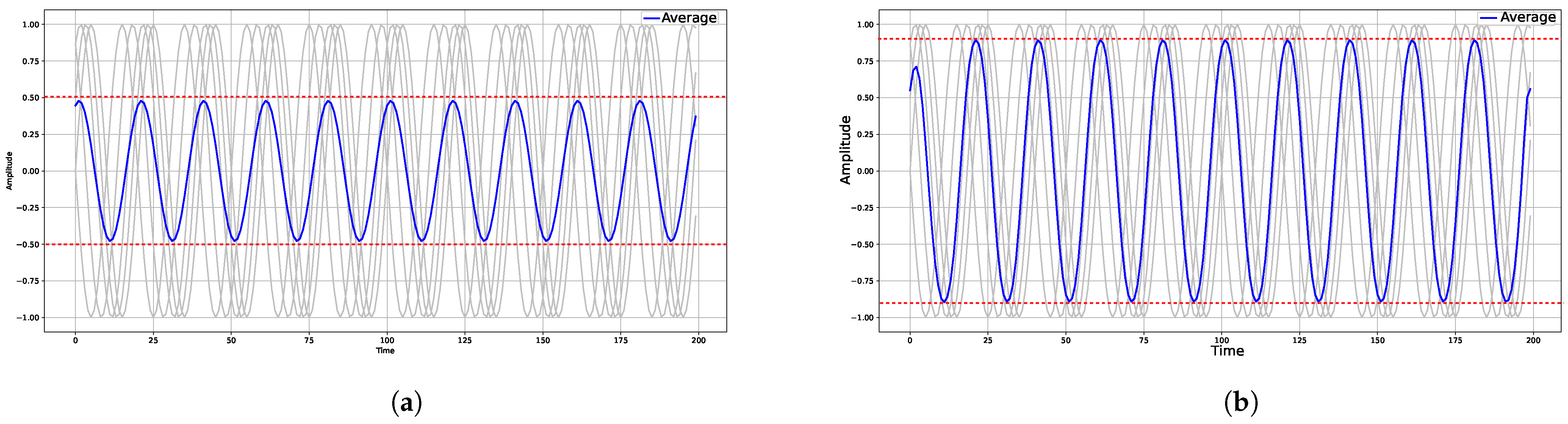
Although pre-processing techniques have proved to be useful, they often induce challenges of their own. In reality, this will be evident if the techniques are not properly configured or if the right technique is not utilized. In this respect, the quality of cluster-level forecasting is often dependent on the separability of clusters, the correlation among cluster members, and the quality of cluster centroids [11,14]. If, for instance, we focus on the cluster centroids (averages), we at times find them being utilized as representatives while fitting univariate or multivariate forecasting models [11]. However, in practice, time series cluster centroids are often significantly affected by temporal distortion, which misaligns patterns (shapes) [15,16]. For instance, in Figure 1, we show a cluster of 50-Hertz sinusoids (sin signals) that have phase differences of . We also show the cluster centroids (averages) that are estimated using an arithmetic mean (shown in Figure 1a) and the soft dynamic time warping barycenter averaging (SDBA) (shown in Figure 1b) [17]. The average estimated using the arithmetic mean is smaller, due to the presence of a phase shift (temporal distortion). In general, in practice, temporal distortion often forces the arithmetic mean to aggregate shapes in a destructive manner [17,18]. Therefore, we often expect a cluster-level forecasting model that is based on an arithmetic mean to be affected by underprediction. In addition to this, the impact of a temporal shift is not limited to the distortion of the cluster centroids. A sub-optimal cluster centroid could also lead to the grouping of members that have no significant correlation (similarity). This in turn could affect the quality of cluster-level predictions that aim at capturing spatial correlations via clustering [11,14].
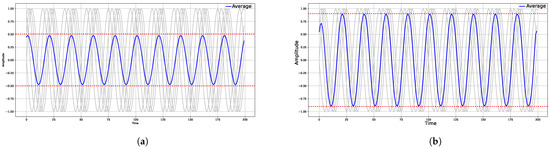
Figure 1.
A demonstration of the impact of temporal distortion on the estimation of cluster centroids. (a) An arithmetic mean. (b) An average estimated using SDBA.
With these observations in mind, in this paper, we propose to utilize a neural network arrangement for cluster formation and centroid estimation. In this regard, we show the advantage of utilizing representation learning, which aims to identify patterns that are presumed to be useful for cluster formation in the latent space of neural networks [19]. Moreover, we also propose to utilize a neural network architecture that is able to estimate time-domain cluster centroids from latent representations [18]. In reality, the utilization of neural networks for the cluster formation and centroid estimation is expected to be advantageous as a result of at least one factor, i.e., transfer learning [20]. In this regard, neural networks are known to be good at generalizing for a range of unseen datasets. Therefore, well-organized and trained clustering and centroid estimation networks are capable of generating clusters and centroids without the need for costly re-runs, i.e., if additional datasets (base stations) become available.
We have organized the rest of the paper into three additional sections. In Section 2, we give a brief review of different clustering and forecasting techniques. Following this, i.e., in Section 3, we present the methodology used in this study. In Section 4, we present the experimental evaluations. Finally, in Section 5, we present our concluding remarks.
2. Background
2.1. A Brief Review of Common Time Series Forecasting Techniques
On a holistic level, the different time series forecasting methods can be grouped into [1,5,10]:
- Statistical models that aim to explicitly model time series patterns using domain knowledge.
- Deep-learning-based models that learn temporal dynamics in a purely data-driven way and without explicit formulations.
In practice, we find both categories of forecasting approaches deployed in wireless network traffic prediction problems. Forecasting models that are deployed in this application domain could be either one of the two or a hybrid of both approaches [2,9,10,11,12]. In general, in this domain, one of the dominant knowledge-driven forecasting approaches is the S-ARIMA forecasting model. The main driving force behind this dominance is the seasonal nature of most mobile traffic data [2,6,9]. For instance, we expect base stations located in residential areas to have a cyclic peak traffic demand in the early mornings, late at night, and at weekends. The S-ARIMA model is found to be capable of modeling such seasonalities by linearly combining the forecasts of autoregressive (AR) and moving average (MA) models () [1,5]. However, in practice, increasing (decreasing) trends within datasets have been found to introduce offsets into predicted values. Consequently, S-ARIMA incorporates a difference operation, which is indicated with the keyword I(d). Moreover, to account for seasonality, it treats the seasonal and non-seasonal parts of the data independently. In general, assuming a (1 − L) lag operator, a S-ARIMA model is mathematically represented as [1]:
where the and orders of polynomials are used for AR() and MA() coefficients, i.e., for the non-seasonal and seasonal parts. The parameters d and D are also used to represent the differencing operation performed on the non-seasonal and seasonal parts of the data. Moreover, , and are the value of a series at t, its residual term, and a constant.
In practice, there are also cases where the underlying data could have patterns that cannot be captured with linear models [8,11]. When this is the case, researchers often propose deploying neural networks that are capable of performing nonlinear transformations. In this regard, neural networks that are based on the long short-term memory (LSTM) method are often found to be efficient [2,10]. This is because these networks are capable by design of capturing the dependencies between time stamps, which is a useful characteristic in time series forecasting. However, in some cases, combining S-ARIMA and neural networks has been proposed, to better capture the seasonal, linear, and nonlinear aspects of an underlying series [8,11]. We now conclude this section and proceed to the discussion of time series clustering techniques.
2.2. A Brief Review of Time Series Clustering Techniques
Like time series forecasting, time series clustering is also an intensively investigated temporal data mining technique [15,21,22]. In general, we can broadly categorize time series forecasting as either distance- or features-based. In distance-based approaches, clustering techniques utilize distance metrics either to group series around their centroids or to group them in a hierarchical manner [22,23]. However, in practice, distance-based approaches are often expected to incorporate some type of temporal alignment technique, to overcome the impact of temporal distortion. When this is the case, the most frequently proposed alignment technique is dynamic time warping (DTW) [24]. However, the incorporation of DTW into the clustering process often increases the computational complexity of the clustering process [16]. With this understanding, in recent years, researchers have proposed performing clustering by utilizing latent space embedding of neural networks [19,21]. For instance, in [19], the authors proposed deep embedding clustering (DEC), which uses a denoising autoencoder to extract latent features from the input series. The latent features are then grouped into K clusters by first computing the soft cluster assigning given in (3).
In (3), is a latent embedding corresponding to a time series , where . Moreover, is the arithmetic mean of the latent embedding corresponding to a cluster. In reality, the soft cluster assignment computes cluster labels based on the likelihood of latent features under the Student t-distribution. In order to make the soft assignments meaningful, the authors proposed to define the auxiliary distribution () given in (4). Finally, the network was forced to minimize the Kullback–Leibler (KL) divergence between its soft assignments and the auxiliary distribution (4).
In this paper, we propose to cluster base stations using the DEC setup. However, one minor inconvenience is that the DEC setup cannot generate time-domain cluster centroids. We propose to overcome this limitation by utilizing a multitasking autoencoder, which is set to perform multi-class classification and reconstruction. This configuration was proposed in [18], in order to estimate the averages of multi-class temporal datasets from their latent embedding. With this in mind, we will next present the methodology used.
3. Methodology
3.1. Proposed Network Architecture
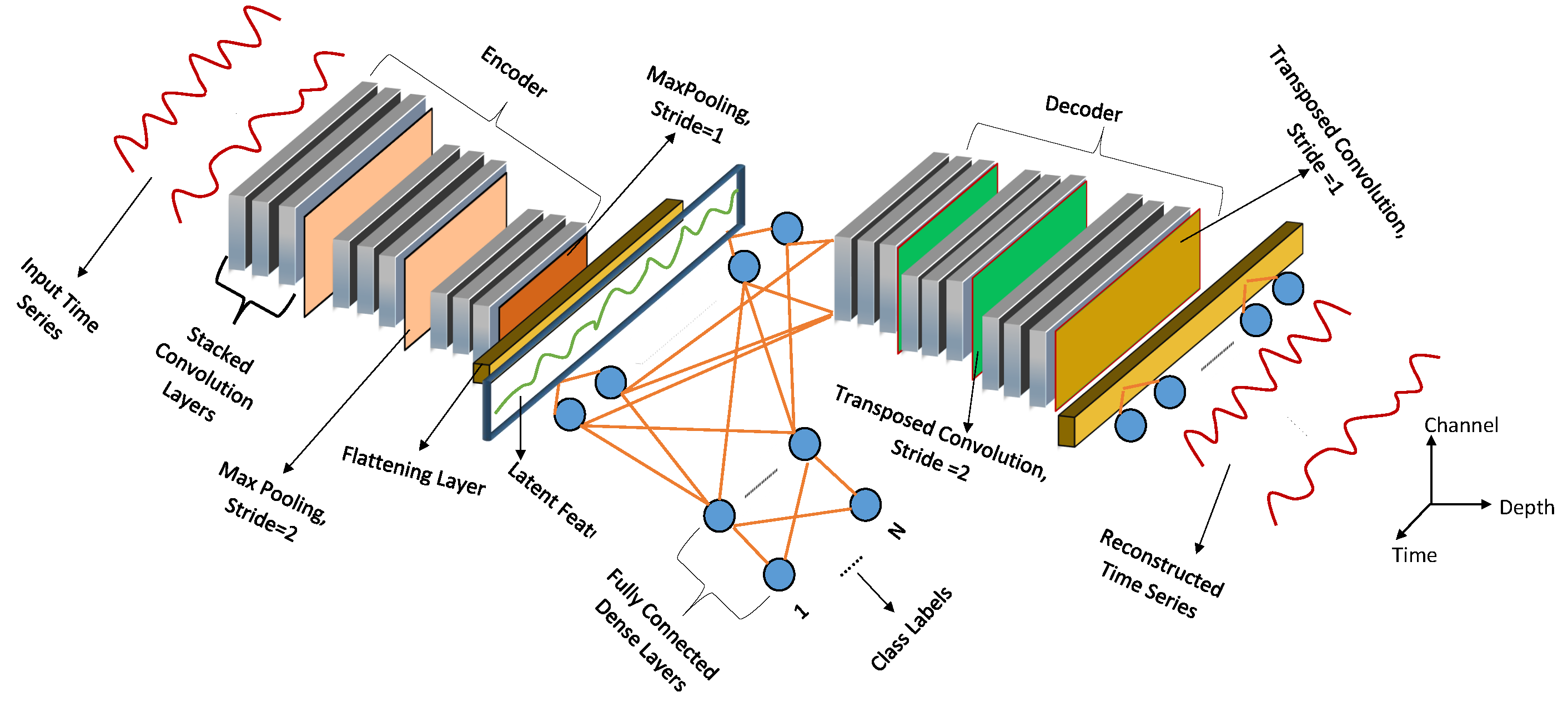
In this study, we utilized the multitasking architecture shown in Figure 2, in order to estimate time-domain cluster centroids. Moreover, we also used the architectures shown at the encoder for deep embedding clustering under the DEC arrangement. In general, the multitasking setup optimizes for reconstruction and the multi-class classification losses given in (5), where are input and reconstructed time series in . Moreover, are the softmax activation values (the likelihood) of a series belonging to category (Cat) [18]. In terms of layer arrangements, the multitasking network is constructed from transposed and normal convolutional, max-pooling, flattening, and dense layers [25].
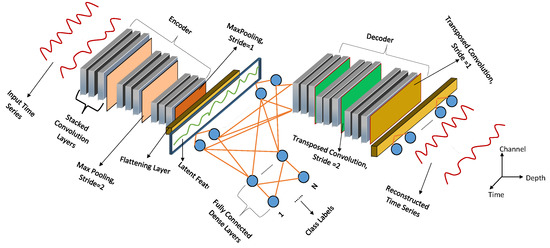
Figure 2.
Neural network architecture utilized for cluster centroid estimation.
In reality, the layer arrangements are motivated by the layer configurations observed in the Visual Geometry Group-16 (VGG16) architecture [26]. Overall, we configured the convolutional and max-pooling layers with a kernel size of 3. Moreover, we configured the transposed convolutions to have a stride of 2. In contrast, the non-transposed convolutional layer and the encoder’s last max-pooling layer had a stride of 1. Furthermore, the number of neurons in the encoder’s dense layer was set to . Moreover, we configured the dense layers of the three classifiers to have , , and K neurons, where K is the number of clusters. Finally, we set the number of neurons for the decoder’s dense layer to 2688. In terms of layer activation, we utilized a rectified linear unit (ReLU) activation function on most of the proposed neural network’s layers. However, for the first encoder’s convolutional layer and the last decoder’s dense layer, we utilized a linear activation function. Finally, we set the classifier’s last dense layer to use a softmax activation function [20,25].
3.2. Datasets
The datasets used were collected from 729 base stations providing wireless data services to regions located within Addis Ababa, Ethiopia. In order to define the temporal datasets, 24 h of data traffic measurements were taken for four consecutive months, i.e., from September 2019 to the end of December 2019. Hence, we obtained 729 temporal datasets that were 2688 time stamps long.
3.3. Experimental Setup
In order to evaluate the proposed approach, we first converted the datasets from terabytes to gigabytes by dividing by 1024. We then took the encoder and decoder portion of the multitasking setup and trained it for a reconstruction loss, i.e., using the first part of (5). Following this, we took the encoder portion of the trained autoencoder and trained it for 1500 epochs using the objective function given in (4). We then used the network to predict cluster labels for the latent embedding of input datasets. Next, we used the labeled series to train the full multitasking setup using (5). This training was performed in order to generate time-domain centroids (averages) for the clustered latent space representations. After training, we estimated time-domain cluster centroids using the decoder portion of the multitasking autoencoder and by taking the arithmetic mean of the latent space represenations. We then took the estimated centroids and fitted a D-SARIMA model, which was implemented in R [27]. The model fitting was performed using a segment of the estimated cluster centroids, i.e., a segment that corresponded to months of traffic measurements. However, in addition to segmenting the centroids, we also identified the most strongly correlated cluster centroids. We used these centroids as exogenous variables of one another while fitting the D-SARIMA model. This, in turn, becomes useful for capturing the spatial correlation among base stations that is evident due to land use.
Finally, we used the D-SARIMA models that were fitted to the cluster centroids to generate weeks of predictions for individual cluster members. However, in order to generate the predictions, we substituted the centroid segments used for model fitting with the corresponding segments of the individual cluster members. In this way, it is possible to test the representativeness of the coefficients learned using the segments of the cluster centroids. Finally, we assessed the quality of the predictions using the root mean square (RMS) error and mean absolute error (MAE), as given in (6). As a comparison, we performed the same evaluations using the TSLearner implantation of K-means and its variant, DBA K-means [16,23,28].
4. Experimental Results and Discussion
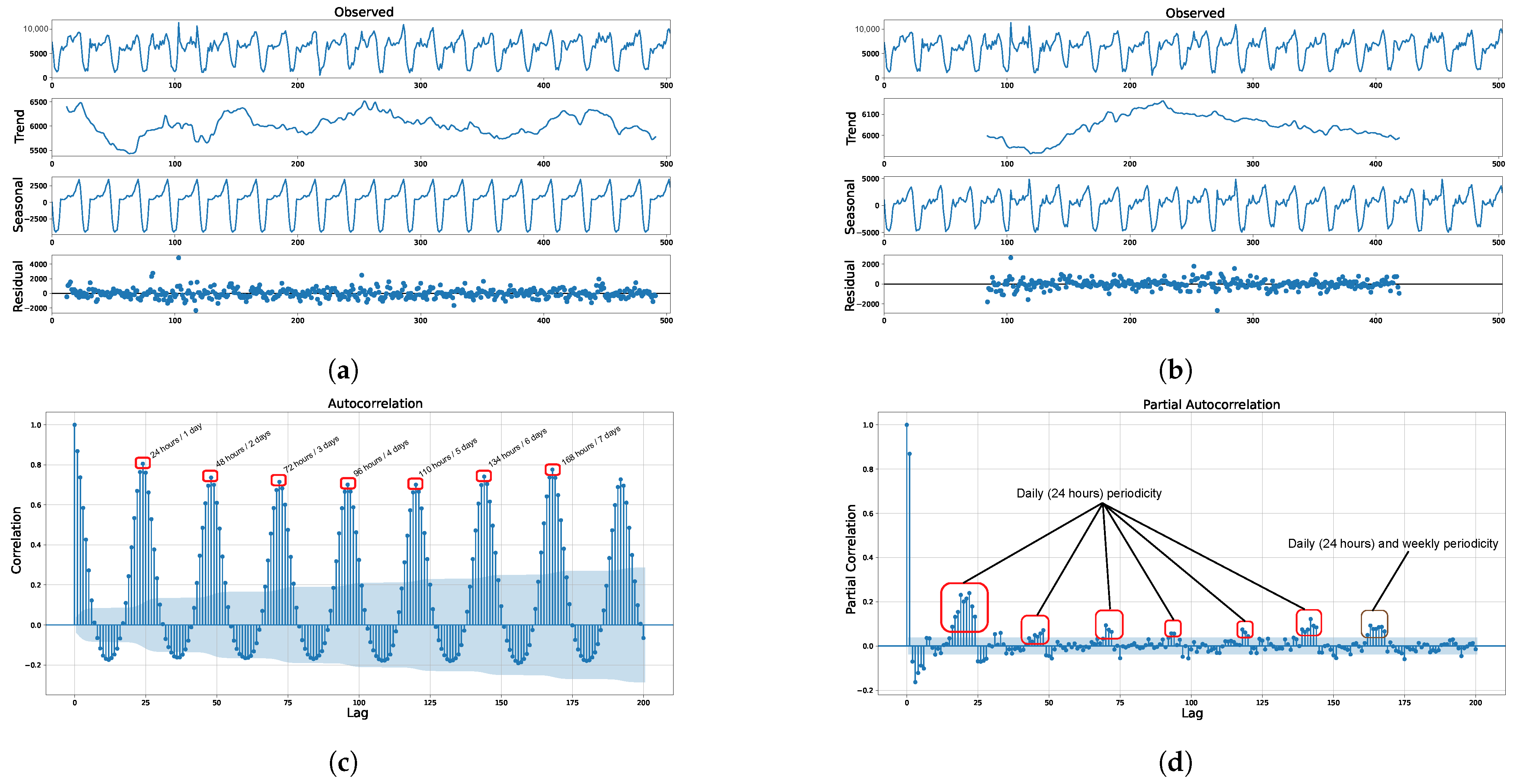
Prior to any model training or fitting, we first assessed the inter-cluster inertia of the traffic datasets, i.e., we determined the optimal number of clusters (K). In this regard, we first conducted a basic K-means clustering for different values of K. We then observed the average within-group squared sum (WGSS) for different values of K. From this observation, we found that five clusters sufficiently minimized the inter-cluster inertia. Next, we decomposed the datasets into their trend, seasonal, and residue components. Moreover, we conducted autocorrelation (AC) and partial autocorrelation (PAC) analyses of the datasets in order to determine the period of the seasonalities. Figure 3a,b show that the datasets have seasonal and trend components. Moreover, Figure 3c,d show that there are two seasons, i.e., a daily (24 h) season and a weekly (168 h) season. Therefore, we decided to deploy a double seasonal ARIMA (D-SARIMA) model rather than an S-ARIMA model.
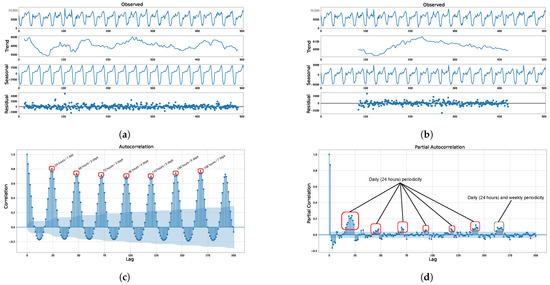
Figure 3.
Demonstration of the seasonality of the data traffic. (a) Daily seasonality. (b) Weekly seasonality. (c) Autocorrelation. (d) Partial autocorrelation.
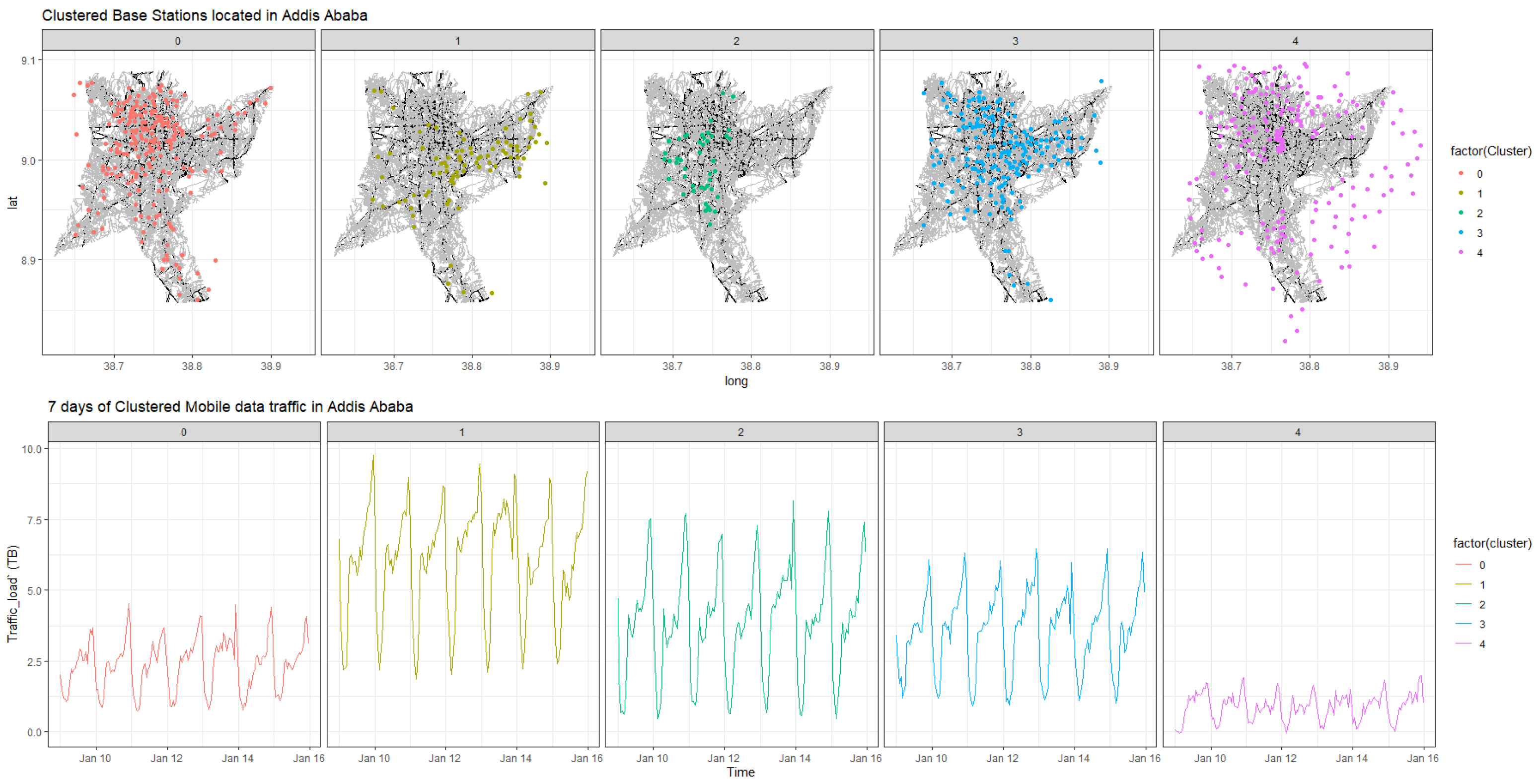
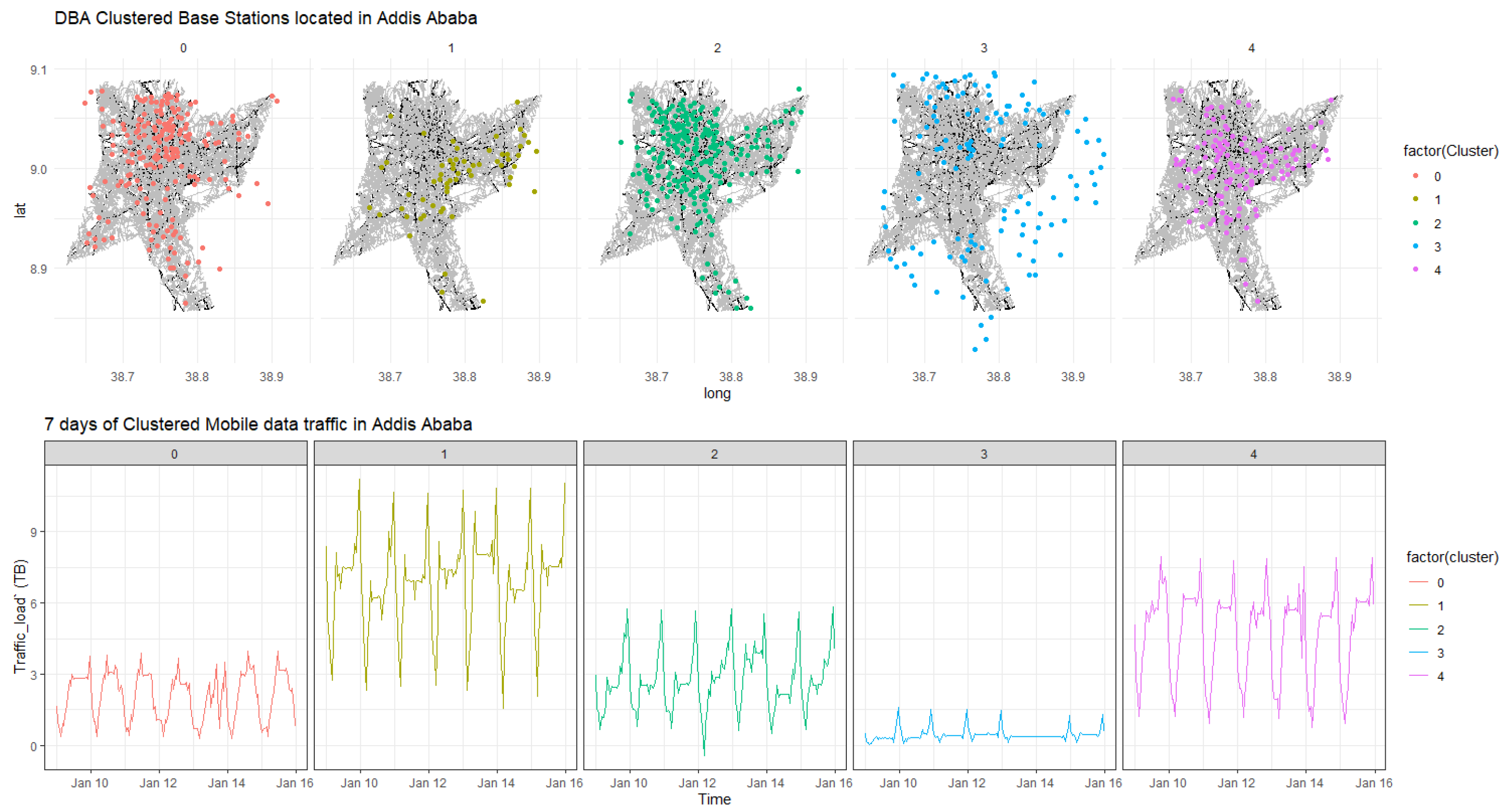
We then used R’s auto.sarima package to determine the optimal model parameters for D-SARIMA and . In this regard, we found that D-SARIMA , gave a better validation error. Therefore, we first clustered the base stations into five groups using the DEC arrangement. We then plotted the clusters on the map of Addis Ababa in order to visually assess whether the clusters had a geographical meaning, as shown in Figure 4.
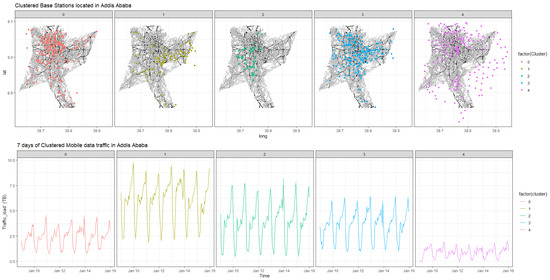
Figure 4.
Geographical location of clusters corresponding to base stations within Addis Ababa.
In general, the clustering algorithm identified geographical locations that correlated with the offered traffic demand. For instance, cluster 1 corresponded to the areas locally known as “Megenagna” and “Bole”. These locations are known to accommodate large entertainment facilities and the country’s largest airport. Additionally, the locations corresponding to cluster 2 accommodate governmental and non-governmental institutions, universities, residential areas, and embassies. Furthermore, cluster 0 and cluster 3 corresponded to mixed use areas that are densely populated, such as “Cherkos” and “Autobis Tera”. Finally, cluster 4 was a purely residential area that is sparsely populated. Overall, the DEC arrangement identified geographical locations that correlated with the amplitudes of the centroids. The alternative clustering also identified similar patterns. However, we observed minor distortions in the centroids of the DBA K-means clustering. We associated these distortions with the sensitivity of DBA to the offset (trend) that is evident in the datasets. Figure 5 demonstrates DBA’s response to the offsets, which are manifested as sharp spikes.
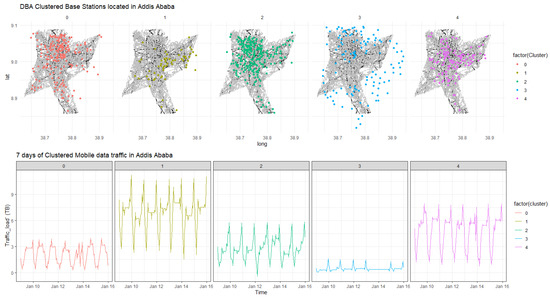
Figure 5.
Clusters and cluster centroids estimated by DBA K-means.
We next compared the performances of the D-SARIMA models fitted on the cluster centroids estimated using the different clustering techniques. In this regard, we made two types of predictions. First, we predicted cluster members using D-SARIMA models that were fitted on the cluster centroids, as discussed in the Experimental Setup section. In Table 1, these predictions are differentiated using the keyword CS. In addition to this, as a benchmark, we made similar predictions using D-SARIMA models that were fitted on the individual cluster members. In Table 1, these prediction are differentiated using the keyword BS.

Table 1.
Comparison of cluster-level and data-level forecasting.
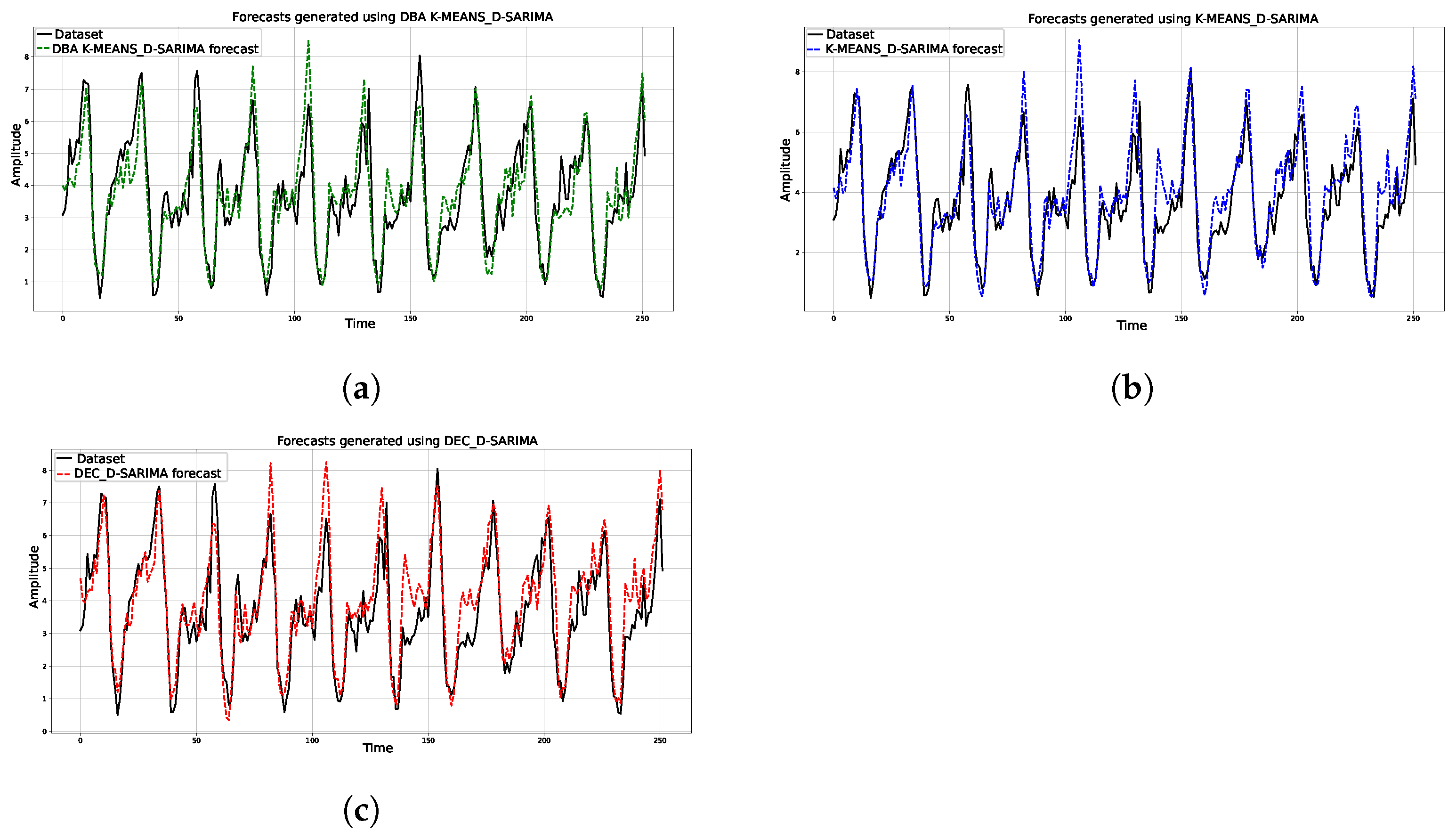
We can interpret the results shown in Table 1 from two different angles. First, we can note that whatever the utilized clustering technique, cluster-level forecasting approaches better captured the dynamics of the underlying data. This is evident, because we have incorporated the spatial information by using highly correlated cluster centroids as exogenous variables. In addition to this, we can also note that the representation learning approach had the lowest aggregate prediction error. This, in turn, implies that the approach is able to overcome the impact of temporal distortion either on cluster formation or on centroid estimation. We conclude this section by presenting the forecasts generated by the three approaches for one of the base stations. For the forecasts shown in Figure 6, the D-SARIMA based on representation learning achieved RMSE and MAE values of 0.758 and 0.596. In contrast, the DBA K-means and basic K-means approaches achieved RMSE and MAE values of 0.802 and 0.617, and 0.669 and 0.847.
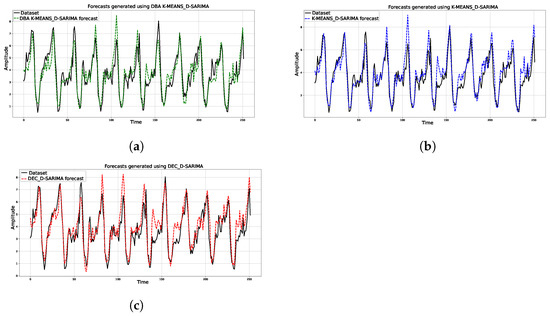
Figure 6.
Example forecasts generated using K-means, DBA K-means, and DEC clustering multitasking autoencoder centroid estimation. (a) DBA-K-means-based forecasts. (b) K-means-based forecasts. (c) DEC and multitasking autoencoder based forecasts.
5. Conclusions
In this paper, we argued that the effect of temporal distortion on cluster formation and cluster centroid estimation cannot be ignored. With this in mind, we proposed a representation-learning-based clustering and cluster centroid estimation approach for cluster-level forecasting. We showed that this approach has the ability to better capture the spatial correlation evident among base stations within wireless communication networks. In general, to validate our argument we only utilized a basic linear forecasting model. However, in reality, the potential of the proposal is not limited to this. In our future work, we aim to assess the improvement in the quality of forecasts using either neural-network-based forecasting techniques or a hybrid of linear and neural-network-based forecasting approaches.
Author Contributions
Conceptualization, Methodology, Software, Validation, Formal Analysis, Investigation, and Data Curation: T.T.D. and B.S.S.; Original Draft Preparation: T.T.D.; Supervision, Review, and Editing: M.D., J.W., D.H.W., S.P. and G.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was conducted under the Ethio-France PhD. program.
Data Availability Statement
The datasets utilized for experimental evaluation are obtained from Ethio Telecom. The authors could make the datasets available up on request and with the consent of the network operator.
Acknowledgments
The authors would like to thank the French Embassy for Ethiopia and the African Union and the former Ethiopian Ministry of Science and Higher Education (MOSHE) for supporting the PhD program under which this research was conducted.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fotios, P.; Daniele, A.; Vassilios, A.; Babai, M.Z.; Barrow, D.K.; Taieb, S.B.; Bergmeir, C.; Bessa, R.J.; Bijak, J.; Boylan, J.E.; et al. Forecasting: Theory and practice. Int. J. Forecast. 2022, 38, 705–871. [Google Scholar]
- Azari, A.; Papapetrou, P.; Denic, S.; Peters, G. Cellular Traffic Prediction and Classification: A Comparative Evaluation of LSTM and ARIMA. In Discovery Science; Kralj Novak, P., Šmuc, T., Džeroski, S., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 129–144. [Google Scholar]
- Chen, G. Spatiotemporal Individual Mobile Data Traffic Prediction; Technical Report RT-0497; INRIA Saclay—Ile-de-France: Leyon, France, 2018. [Google Scholar]
- Xu, F.; Lin, Y.; Huang, J.; Wu, D.; Shi, H.; Song, J.; Li, Y. Big Data Driven Mobile Traffic Understanding and Forecasting: A Time Series Approach. IEEE Trans. Serv. Comput. 2016, 9, 796–805. [Google Scholar] [CrossRef]
- Wei, W. Time Series Analysis: Univariate and Multivariate Methods; Pearson Addison Wesley: Boston, MA, USA, 2006. [Google Scholar]
- Shu, Y.; Yu, M.; Liu, J.; Yang, O. Wireless traffic modeling and prediction using seasonal ARIMA models. In Proceedings of the IEEE International Conference on Communications, Anchorage, AK, USA, 11–15 May 2003; Volume 3, pp. 1675–1679. [Google Scholar]
- Montero-Manso, P.; Hyndman, R.J. Principles and algorithms for forecasting groups of time series: Locality and globality. Int. J. Forecast. 2021, 37, 1632–1653. [Google Scholar] [CrossRef]
- Zeng, D.; Xu, J.; Gu, J.; Liu, L.; Xu, G. Short Term Traffic Flow Prediction Using Hybrid ARIMA and ANN Models. In Proceedings of the 2008 Workshop on Power Electronics and Intelligent Transportation System, Guangzhou, China, 2–3 August 2008; pp. 621–625. [Google Scholar]
- Zhou, B.; He, D.; Sun, Z. Traffic Modeling and Prediction using ARIMA/GARCH Model. In Modeling and Simulation Tools for Emerging Telecommunication Networks; Springer: Boston, MA, USA, 2006; pp. 101–121. [Google Scholar]
- Zhang, C.; Patras, P.; Haddadi, H. Deep Learning in Mobile and Wireless Networking: A Survey. IEEE Commun. Surv. Tutor. 2019, 21, 2224–2287. [Google Scholar] [CrossRef]
- Shawel, B.S.; Debella, T.T.; Tesfaye, G.; Tefera, Y.Y.; Woldegebreal, D.H. Hybrid Prediction Model for Mobile Data Traffic: A Cluster-level Approach. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar]
- Jaderberg, M.; Simonyan, K.; Zisserman, A.; Kavukcuoglu, K. Spatial Transformer Networks. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Jose, CA, USA, 2015; Volume 28. [Google Scholar]
- John, G.P.; Masoud, S. Fundamentals of Communication Systems; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Sfetsos, A.; Siriopoulos, C. Time series forecasting with a hybrid clustering scheme and pattern recognition. IEEE Trans. Syst. Man Cybern. Part A Syst. Humans 2004, 34, 399–405. [Google Scholar] [CrossRef]
- Aghabozorgi, S.; Shirkhorshidi, A.S.; Wah, T.Y. Time-series clustering–a decade review. Inf. Syst. 2015, 53, 16–38. [Google Scholar] [CrossRef]
- Petitjean, F.; Forestier, G.; Webb, G.I.; Nicholson, A.E.; Chen, Y.; Keogh, E. Faster and more accurate classification of time series by exploiting a novel dynamic time warping averaging algorithm. Knowl. Inf. Syst. 2016, 47, 1–26. [Google Scholar] [CrossRef]
- Petitjean, F.; Gançarski, P. Summarizing a set of time series by averaging: From Steiner sequence to compact multiple alignment. Theor. Comput. Sci. 2012, 414, 76–91. [Google Scholar] [CrossRef]
- Terefe, T.; Devanne, M.; Weber, J.; Hailemariam, D.; Forestier, G. Time Series Averaging Using Multi-Tasking Autoencoder. In Proceedings of the 2020 IEEE 32nd International Conference on Tools with Artificial Intelligence (ICTAI), Baltimore, MD, USA, 9–11 November 2020; pp. 1065–1072. [Google Scholar]
- Xie, J.; Girshick, R.; Farhadi, A. Unsupervised Deep Embedding for Clustering Analysis. In Proceedings of the 33rd International Conference on International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; Volume 48, pp. 478–487. [Google Scholar]
- Vasilev, I.; Slater, D.; Spacagna, G.; Roelants, P.; Zocca, V. Python Deep Learning: Exploring Deep Learning Techniques and Neural Network Architectures with PyTorch, Keras, and TensorFlow, 2nd ed.; Packt Publishing: Birmingham, UK, 2019. [Google Scholar]
- Lafabregue, B.; Weber, J.; Gançarski, P.; Forestier, G. End-to-end deep representation learning for time series clustering: A comparative study. Data Min. Knowl. Discov. 2021, 36, 29–81. [Google Scholar] [CrossRef]
- Leonard, K.; Peter, J.R. Finding Groups in Data: An Introduction to Cluster Analysis; John Wiley: Hoboken, NJ, USA, 1990. [Google Scholar]
- Bock, H.H. Origins and extensions of the -means algorithm in cluster analysis. J. Électron. d’Histoire Probab. Stat. 2008, 4, 18. [Google Scholar]
- Sakoe, H.; Chiba, S. Dynamic programming algorithm optimization for spoken word recognition. IEEE Trans. Acoust. Speech Signal Process. 1978, 26, 43–49. [Google Scholar] [CrossRef]
- Chollet, F. Keras. 2015. Available online: https://keras.io (accessed on 1 May 2022).
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. In Proceedings of the 3rd International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Hyndman, R.J.; Khandakar, Y. Automatic Time Series Forecasting: The forecast Package for R. J. Stat. Softw. 2008, 27, 1–22. [Google Scholar] [CrossRef]
- Tavenard, R.; Faouzi, J.; Vandewiele, G.; Divo, F.; Androz, G.; Holtz, C.; Payne, M.; Yurchak, R.; Rußwurm, M.; Kolar, K.; et al. Tslearn, A Machine Learning Toolkit for Time Series Data. J. Mach. Learn. Res. 2020, 21, 1–6. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).