On the Aerodynamic Characteristics of the Aurel Persu Car ^†

Abstract

This study investigates the aerodynamics of Romanian engineer Aurel Persu’s car through wind tunnel experiments involving force measurements, Particle Image Velocimetry (PIV), and CFD simulations. Tests using scale models revealed significant flow separation behind the cabin. The measured drag coefficient is C_D = 0.364 at 33 m/s, showing moderate sensitivity to Reynolds number. CFD simulations using the unsteady STAR CCM+ solver with a k-ω SST turbulence model produced a slightly lower drag coefficient (C_D = 0.353) due to delayed separation. The good agreement between experimental and numerical results validates the modeling approach and highlights aerodynamic limitations around the front and roof. Despite these limitations, the model achieved aerodynamic performance that was exceptional for its time and remained competitive with mainstream production vehicles well into the latter half of the 20th century.

1. Introduction

Automotive aerodynamics is a complex, multidisciplinary field that affects multiple aspects of vehicle performance. External airflow management contributes to stability, handling, wind noise reduction, and the cleanliness of surfaces like windows, mirrors, and headlights. It also aids in cooling components such as brakes and exhaust systems. Additionally, aerodynamic principles govern internal airflow for engine cooling and effective heat rejection, while also supporting cabin climate control to ensure passenger comfort.

Although all of these functions contribute to the overall aerodynamic performance of a vehicle, aerodynamic drag remains the most prominent and widely analyzed factor due to its direct influence on fuel consumption, emissions, and driving range. The drag coefficient (C_D) has become a key design benchmark, analogous to the compression ratio in internal combustion engines, and is widely used as a standardized metric for aerodynamic efficiency. The aerodynamic drag force (D) increases with the square of vehicle velocity (D ∝ V²), making it the dominant resistive force at highway speeds. For a typical mid-sized car traveling at 100 km/h, aerodynamic drag accounts for approximately 75–80% of the total driving resistance [1]. As a result, reducing drag is one of the most effective strategies for improving vehicle efficiency. Historically, drag reduction was motivated primarily by the pursuit of higher top speeds. In recent decades, however, design priorities have shifted toward lowering fuel consumption and minimizing greenhouse gas emissions, in response to increasingly stringent environmental regulations and growing consumer expectations for sustainability. This interest started with the 1973 and 1979 oil crises, which prompted automakers to focus on advancements in car aerodynamics. Returning to present times, the electrification of propulsion has given another push to the car aerodynamics and in this context, it is worth noting the current efforts of the OEMs to reduce the aerodynamic drag of the pure electric vehicles (PEVs), mainly aiming to increase the range (e.g., the Mercedes-Benz VISION EQXX boasts a drag coefficient of 0.17 [2], which is a benchmark for aerodynamics of vehicles). This aspect is more valid for PEVs, as here, the external aerodynamics is also relevant in the case of decelerations, thanks to the regenerative braking; i.e., since the energy recovered while decelerating is harvested from the energy remaining after deducting the energy loss in the vehicle’s interaction with the environment (rolling and aerodynamic drags) from the vehicle’s kinetic energy, it follows that the smaller the air resistance, the greater the energy recovered during vehicle’s deceleration. An example of a study aiming to find the benefits of active aerodynamics on energy recuperation in electrified vehicles is given in [3].

A notable early attempt to improve aerodynamic efficiency is the automobile designed by Romanian engineer Aurel Persu, developed in 1922. Persu’s concept challenged traditional automotive design by enclosing the wheels within the streamlined body and approximating the ideal teardrop shape, as described in his patent [4]. Persu’s car is described by Hucho [1] as resembling the “ideal” half-body; however, Hucho does not mention any specific value for the drag coefficient. The vehicle is often cited—particularly in non-academic sources—as having achieved a drag coefficient of approximately C_D = 0.28, although no experimental measurements have been published to substantiate this claim. It is likely that this figure originated by analogy with the Rumpler Tropfenwagen, a contemporary streamlined vehicle that underwent wind tunnel testing at 1:7.5 scale in the AVA facility in Göttingen and was later re-evaluated by Volkswagen engineers in 1979 on a full-scale vehicle, confirming a C_D value of approximately 0.28 [1]. Another historic aerodynamic one-volume teardrop-shaped car was the Schlorwagen, which was tested in the wind tunnel of AVA and yielded a drag coefficient of 0.125, [1]. Returning to Persu’s car, however, its visual inspection reveals design elements that deviate from the “ideal” teardrop [3]. In particular, the front section appears relatively blunt, and the roofline may induce flow separation. These characteristics suggest that the actual aerodynamic drag coefficient may be higher than commonly believed, although no direct experimental validation has been performed to test this hypothesis.

The present study aims to provide a rigorous aerodynamic evaluation of the Persu automobile through a combination of experimental and computational methods and to complete previous works [5]. Wind tunnel testing will be conducted using a 1:8 scale model to measure drag forces and moments under controlled conditions. Flow visualization will be carried out via Particle Image Velocimetry (PIV) using a 1:20 scale model to capture qualitative and quantitative insights into flow separation, recirculation, and wake development. The use of scaled models is necessitated by tunnel size limitations and PIV camera resolution and requires careful consideration of Reynolds number effects and geometric similarity. In fact, the different model scales reflect the practical constraints of available experimental facilities while maintaining sufficient resolution for both force and flow measurements.

Complementing the experimental work, Computational Fluid Dynamics (CFD) simulations using STAR-CCM+ will provide detailed insights into the flow field. The simulations will serve to compare with the experimentally measured drag coefficients and help identify the flow mechanisms responsible for the vehicle’s aerodynamic behavior. Special attention will be paid to flow separation zones, wake structure, and surface pressure distribution.

2. Experiments

2.1. Wind Tunnel Facilities

The aim of the present experimental study is to gather sufficient data both for improving numerical modeling approaches and for their validation. Two printed models were used: one for measuring aerodynamic forces and another specifically designed for velocity field measurements around the vehicle. The scale of the first model 1:8, length 575 mm, was determined based on the limitations of the available 3D printing equipment. The second model has a length of 207 mm, selected according to the spatial resolution capabilities of the available PIV equipment. The two different model scales were necessitated by the spatial constraints of the respective measurement techniques while maintaining adequate resolution.

The experiments were conducted in the ENSAM-LIFSE, Paris, France wind tunnel, a closed-circuit Prandtl-type facility [6]. The test section is semi-guided and has dimensions of 1.35 m × 1.65 m with a length of 2 m. The cross-sectional area of approximately 2.2 m² exceeds the minimum recommended 2 m², as suggested by [1], for aerodynamic testing of scale car models. The return channel measures 3 m × 3 m in cross-section and 6 m in length. It is designed to accommodate wind turbine tests or other large cross-sectional models.

The tunnel is driven by a 3 m diameter fan powered by a 120 kW asynchronous motor. The fan velocity is regulated by a frequency converter, allowing airflow velocities between 1.5 m/s and 35 m/s. A nozzle with a contraction ratio of 12.5 ensures a turbulence intensity below 0.25% in the test section.

The boundary layer thickness at the test section inlet, measured with a hot-wire anemometer, is approximately 40 mm. To reduce its influence on the model, a thin circular plate with sharpened edges and a diameter of 1.6 m is used as a base in the test section. It is positioned 200 mm above the tunnel floor. The vehicle model is mounted at the center of this plate and connected to a six-component aerodynamic balance (Figure 1). It should be noted that the circular plate is not equipped with a moving belt and the wheels remain stationary. In this case, according to [1], the drag coefficient is expected to be slightly lower than that obtained with a moving ground.

2.2. Aerodynamic Drag Measurements

The aerodynamic forces are measured using a balance equipped with strain gauges connected to ML30B carrier-frequency amplifiers, integrated into an MGCplus data acquisition system (HBM GmbH, Darmstadt, Germany). This setup provides a measurement accuracy of 0.04 N within the 0–50 N range. The balance is calibrated before each measurement series using certified reference weights.

The airflow velocity V in the test section is determined by measuring the pressure difference $∆p$ between the settling chamber and the test section. Since the flow velocity in the settling chamber is significantly lower than that in the test section, this pressure difference closely approximates the dynamic pressure of the flow:

$$∆p={\displaystyle \frac{1}{2}}\rho V^2$$

(1)

A precision differential pressure manometer FCO510 (Furness Controls Ltd, Bexhill-on-Sea, UK) was used, offering an accuracy of 0.25% of the reading between 10% and 100% of the full scale.

The nozzle discharge coefficient is very close to 1, confirmed using both a Pitot tube and PIV. Atmospheric pressure was recorded using a mercury barometer, and air temperature was measured with a 4-wire Pt100 sensor. These values were used to calculate air density, which in turn allowed the determination of the free-stream velocity based on the measured differential pressure:

$$V=\sqrt{{\displaystyle \frac{2∆p}{\rho }}}$$

(2)

The entire system is controlled via a LabVIEW 8.5 (National Instruments, Austin, TX, USA) -based interface running on a PC connected to the MGCplus unit. An NI PCIe-6259 acquisition card (National Instruments, Austin, TX, USA) was used for collecting analog signals from temperature and pressure sensors.

It is important to note that the drag and lift forces acting on bluff bodies fluctuate over time. These unsteady loads may, under certain conditions, cause minor flow velocity oscillations in the test section. To capture these variations, pressure, force, and temperature data are sampled at 10 Hz over a 20 s interval. Experimental tests with varying sampling durations confirmed that 20 s is sufficient for statistically converged results.

The Reynolds number in this study is defined using the model length as the reference length and the wind tunnel velocity as the reference velocity. Due to limitations in both model size and flow velocity, full-scale Reynolds numbers could not be achieved. However, the maximum Reynolds number attained during testing was approximately $Re=1.2\times {10}^6$ which is generally sufficient to avoid most low-Reynolds-number effects. To further improve similarity with full-scale conditions, both an increase in model length and the use of turbulence-generating grids [7,8,9,10] may be considered.

The aerodynamic drag coefficient $C_D$ is calculated directly from the measured drag force $F_x$, frontal area $A_m$ obtained from the CFD model, and dynamic pressure $∆p$:

$$C_D={\displaystyle \frac{F_x}{{∆pA}_m}}$$

(3)

The drag force increased approximately eleven-fold as the flow velocity rose from 10 m/s to 33 m/s. As expected, the drag coefficient $c_d$ decreased with increasing Reynolds number, from $C_D=0.364$ at 10 m/s ($Re=3.55\times {10}^5$) to $C_D=0.355$ at 33 m/s ($Re=1.2\times {10}^6$). The estimated uncertainty in the drag coefficient is below 0.75% at the highest velocity and increases to 5.5% at the lowest test velocity, primarily due to the resolution limits of the wind tunnel balance. The lift coefficient (C_L) is negligibly small and effectively zero within the sensitivity range of the balance.

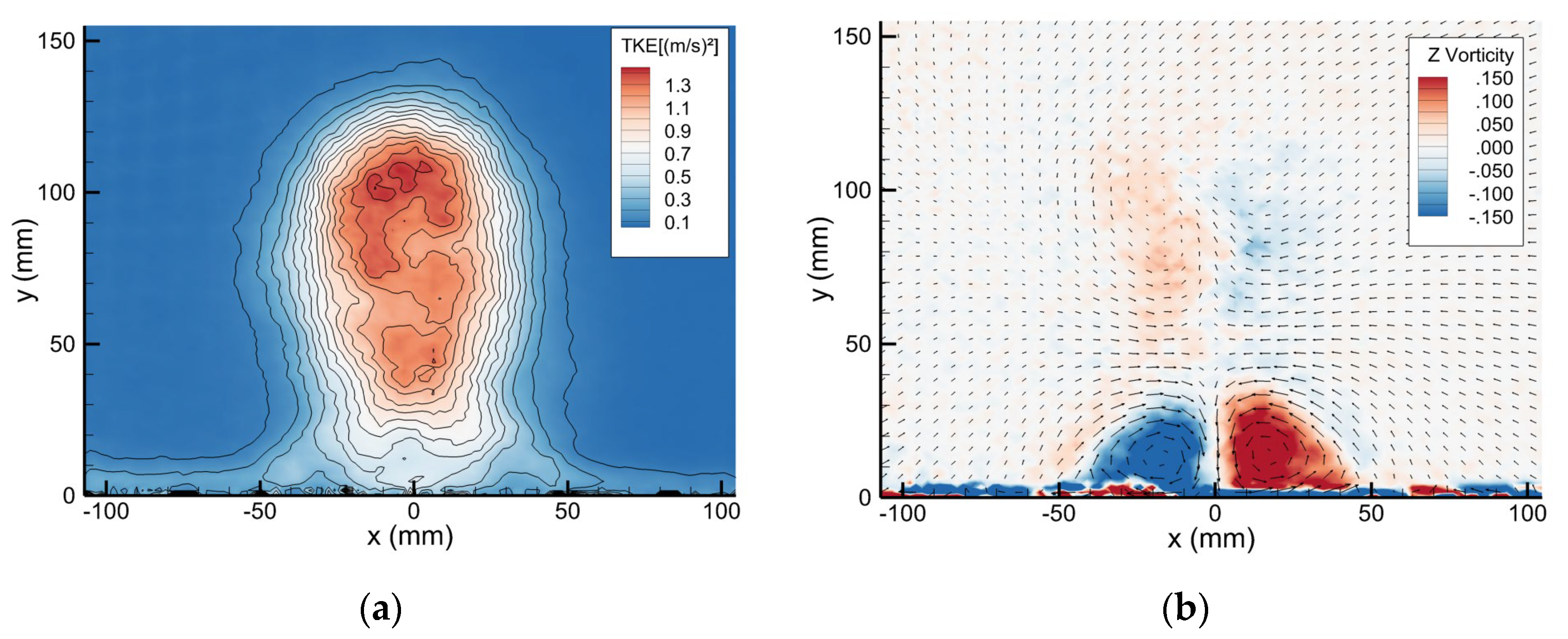
2.3. Particle Image Velocimetry (PIV) Measurements

PIV was employed to measure the velocity field around the vehicle model. This non-intrusive technique provides detailed information on flow structures, including separation zones, which are essential for understanding vehicle aerodynamics [11]. The data also serve as a reference for validating numerical simulations and selecting appropriate turbulence models.

During the PIV experiments, the flow velocity was set to 10 m/s. Olive oil droplets, generated by a 10F03 mist generator (Dantec Dynamics A/S, Skovlunde, Denmark), were used as seeding particles. These droplets, a few microns in diameter, were illuminated by a Nano L 200-15 double-pulse Nd:YAG laser (200 mJ; Litron Lasers Ltd, Rugby, UK) with laser sheet thickness of 3 mm. A FlowSense 4MP Mk2 camera (Dantec Dynamics A/S, Skovlunde, Denmark) captured the particle motion at a frequency of 7 Hz. Image processing was performed using adaptive PIV algorithms. The final vector field was obtained using an 8 × 8 pixel step grid and a minimum interrogation window of 16 × 16 pixels.

The first series was conducted in the symmetry plane of the vehicle using a AF Micro-Nikkor 60 mm f/2.8D lens (Nikon Corporation, Tokyo, Japan). This setup enabled the capture of the velocity field around the entire vehicle, covering an area of 250 mm × 250 mm with a spatial resolution of approximately 1 mm/vector.

The second series was also performed in the vehicle’s symmetry plane, focusing on the cabin region, and employed aAF-S VR Micro-Nikkor 105 mm f/2.8G IF-ED lens (Nikon Corporation, Tokyo, Japan). The longer focal length allowed for a more precise determination of the flow separation point. The measurement area in this case was 130 mm × 130 mm, with an improved spatial resolution of approximately 0.5 mm/vector.

The third series was carried out in a plane perpendicular to the free-stream direction, located 150 mm downstream from the vehicle’s rear end (equivalent to 0.72 vehicle lengths). The aim was to assess the vortex intensity in the vehicle’s wake. To capture all three velocity components, a stereo PIV configuration with two cameras was used. The combination of Nikon AF 60 mm lenses and the camera-to-measurement-plane distance enabled a velocity field measurement area of 230 mm × 230 mm, with a spatial resolution of approximately 0.9 mm/vector.

For each of the three measurement series, reference measurements were also performed in the undisturbed flow field without the vehicle, in order to evaluate the uniformity of the velocity field and to compare the measured velocities as given by Equation (2). For each series measurement, a total of 250 image pairs is used to obtain average velocity field.

Raw PIV images were processed using Dynamic Studio 2015a (Dantec Dynamics A/S, Skovlunde, Denmark).

It should be mentioned that estimating the uncertainty of velocity measurements near solid bodies using PIV is not straightforward, as also discussed in [11,12]. In this case, additional challenges arise due to laser sheet reflections from the model surface, coupled with the limited transparency of proprietary software methods. Instead of relying on generic assumptions to estimate accuracy, a reference PIV measurement was performed in the free stream without the model. The resulting velocity field showed a maximum deviation of less than 2%.

Figure 2a shows the time-averaged velocity field around the model. The stagnation point, where the flow velocity drops to near zero, is located close to the headlight height. Below this point, the flow accelerates to approximately 90% of the free-stream velocity. In the wake region, the velocity drops to around 75%, due to frictional losses along the underbody and additional blockage from the rear axle, which is located below the car underneath.

The highest local acceleration—up to 130% of the free-stream velocity—is observed near the upper edge of the windscreen, where the flow separates from the roof just after the start of the rear side window.

Figure 2b presents a visualization of the flow separation zone based on the time-averaged velocity field. The recirculation region behind the vehicle cabin extends over approximately 25% of the model’s total length. The presence of this low-velocity separation zone accounts for the observed drag coefficient of C_D = 0.364.

It is important to note that many of the vortices observed in the instantaneous velocity fields are considerably larger than the time-averaged recirculation zone. Furthermore, none of the instantaneous flow fields resemble the time-averaged pattern. The separation point is not fixed; instead, it varies over a relatively wide range. To more accurately determine the extent of the separation zone, a second set of velocity field measurements was conducted in the cabin region, as shown in Figure 3a.

To identify the boundaries of the separation region, the turbulence kinetic energy (TKE) was used [7,13]. TKE is calculated as half the sum of the squares of the standard deviations of the fluctuating velocity components u, v and w:

$$TKE={\displaystyle \frac{1}{2}}\left(\overline{{\left(u^{\prime }\right)}^2}+\overline{{\left(v^{\prime }\right)}^2}+\overline{{\left(w^{\prime }\right)}^2}\right)$$

(4)

Figure 3b shows the TKE distribution in the separation region. This provides a clearer indication of the extent of flow detachment, identified as the region where the TKE is significantly higher than in the surrounding flow. In this case, the high-TKE region corresponds to approximately 5% of the total body length.

The aerodynamic wake was further analyzed in a cross-sectional plane perpendicular to the freestream direction, located at a distance of 0.72 model length (L) measured from the rear end of the model. As shown in Figure 4a, the TKE reaches a maximum at a height of approximately 105 mm, which corresponds to 1.18 times the model height. The width of the high-TKE region is comparable to the model’s width.

Additionally, the vorticity in the streamwise direction was examined. The streamwise vorticity field, also shown in Figure 4b, was computed as:

$${\omega }_z={\displaystyle \frac{\partial v}{\partial x}}-{\displaystyle \frac{\partial u}{\partial y}}$$

(5)

Two counter-rotating vortices are observed at a spanwise distance of approximately 0.8 times the model’s width. The presence of these vortices suggests the generation of a very low positive lift force.

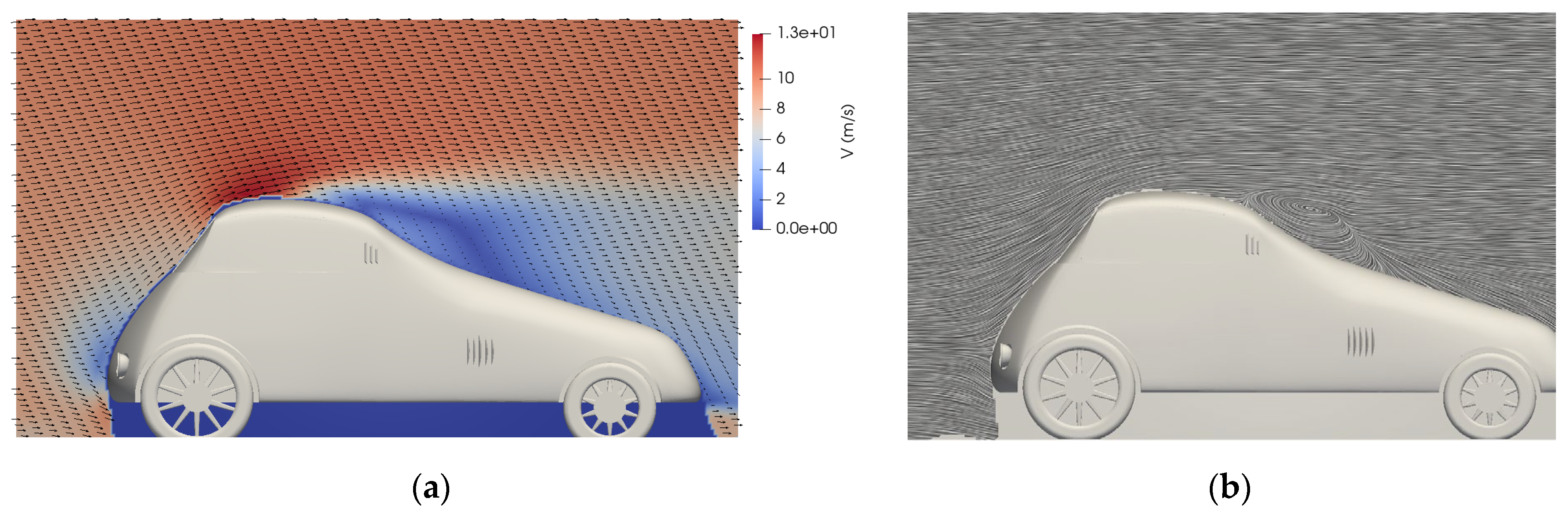
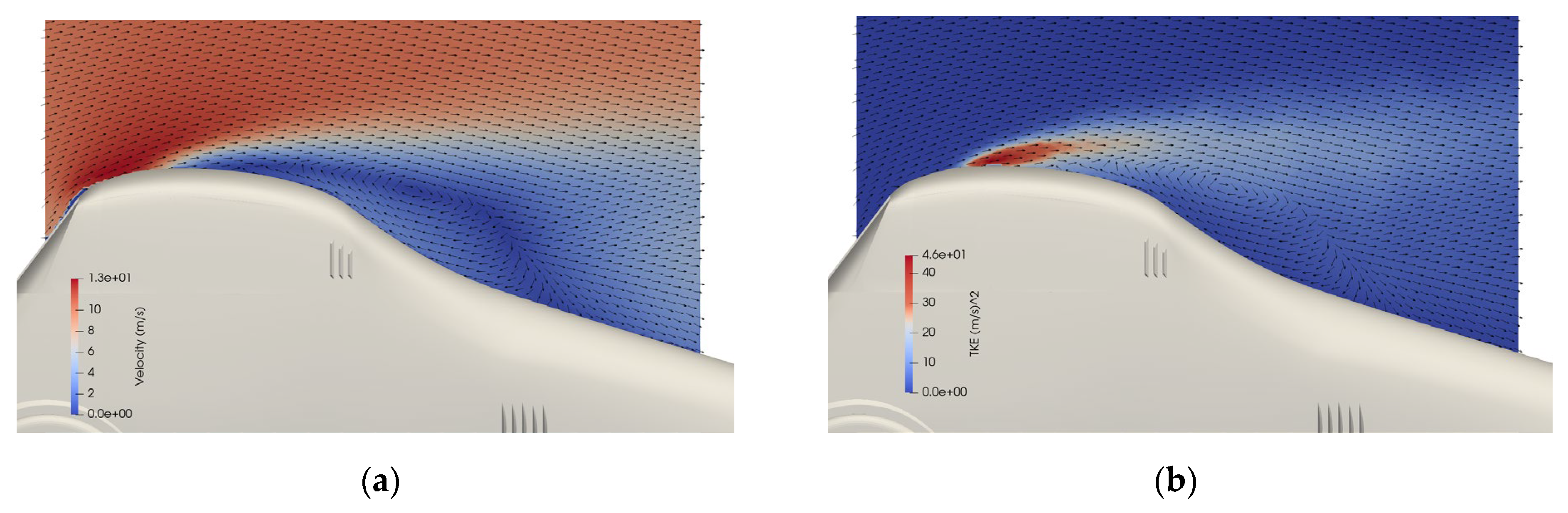
2.4. Discussion of Experimental Results

The velocity field analysis reveals a strong separation and a well-developed recirculation zone behind the vehicle cabin. It can be inferred that the front section of the vehicle is not sufficiently streamlined. The flow accelerates significantly at the end of the windshield and separates shortly thereafter, near the beginning of the roof. This aerodynamic behavior is likely influenced by practical design considerations. Notably, the patent registered by Persu [3] features a front profile with a more teardrop-like shape, suggesting that the current form may deviate from the optimal aerodynamic profile for functional reasons.

Despite the significant difference in Reynolds number between the model and the full-scale vehicle, their drag coefficients are expected to be very similar. This is due to two opposing effects. On one hand, the drag coefficient tends to decrease with increasing Reynolds number, as also pointed out in [13,14,15]. On the other hand, unlike the simplified model, the real car features numerous small external elements that increase aerodynamic resistance. This balance is confirmed by aerodynamic studies of the Rumpler car, where the full-scale vehicle exhibited the same drag coefficient as its 1:7.5 scale model.

3. Numerical Simulations

For the numerical simulation, a model representing an eighth-scale replica of the Persu vehicle was created. The flow domain around the vehicle corresponds to the test section of the wind tunnel. Both the wheels and the road surface beneath the vehicle are stationary. The objective is to develop a simulation model that accurately reproduces the experimental conditions from the wind tunnel tests. The drag coefficient (C_D) is the main output parameter of interest in the simulation, serving as a benchmark for evaluating the agreement between the numerical results and the experimental data.

The STAR CCM+ (18.02.008; Siemens Digital Industries Software, Plano, TX, USA) was employed for simulations. Computational mesh consists entirely of polyhedral cells. To improve the resolution of the boundary layer flow over the vehicle and road surfaces, five layers of prismatic cells were added. The simulations employed the “All-y+” wall treatment [16,17,18,19]. This approach blends low- and high-Re wall treatments, providing accurate results across a wide range of near-wall mesh densities. It adapts to the local y+, delivering consistent predictions even when the wall-cell centroid falls in the buffer region. In the present case, most y+ values lie between 50 and 100, appropriate for high-Re modeling. However, due to local flow complexity, values below 10 also occur. The “All-y+” model is specifically designed to handle such variation.

The computational domain was divided into two main regions. The first region surrounds the vehicle, extending approximately two vehicle widths and two vehicle heights in lateral and vertical directions, and covering the full length of the test section. The second region represents the remaining part of the flow domain in the test section.

The region around the vehicle was further subdivided into three zones:

• An upstream region with undisturbed flow containing approximately 2.3 million cells;
• A region surrounding the vehicle body with around 3.5 million cells;
• A wake region downstream of the vehicle with approximately 2.6 million cells.

The outer region contains about 2.2 million cells, bringing the total cell count for the simulation model to roughly 10.6 million. A detailed mesh independence study was not conducted in this work; however, the mesh parameters were selected based on the authors’ previous experience [4,6,20].

The widely used k-ω SST turbulence model was chosen [21,22], and the flow was assumed to be unsteady. The model’s surfaces were treated as rough walls with a roughness height of 0.2 mm; the roughness limiter was disabled. At the domain inlet, a velocity of 33 m/s and a turbulence intensity of 0.25% were prescribed to replicate the wind tunnel conditions as closely as possible. A pressure outlet boundary condition was applied at the domain exit. On the lateral and top boundaries, a zero-shear stress condition was imposed. These outer boundaries serve to simulate the cross-sectional area ratio between the model and the tunnel section. The boundary layer development in these regions is not expected to significantly affect the vehicle’s aerodynamic drag.

The simulation was performed as an unsteady calculation with a time step of 1.10⁻³ and 10 iterations per time step. Convergence of the solution was achieved after approximately 600 time steps, at which point the time-averaged drag force reached a steady value, resulting in a drag coefficient of C_D = 0.353, which is lower than the experimental value of C_D = 0.364 obtained at the same velocity. The primary reason for this discrepancy is the delayed flow separation from the vehicle roof, as clearly demonstrated in Figure 5a (velocity field in the symmetry plane) and Figure 5b (TKE field in the symmetry plane). The velocity field visualization reveals the extent of the separation bubble, while the TKE distribution indicates regions of high turbulent activity associated with the flow separation process.

In practice, predicting the exact separation line using conventional RANS models remains challenging due to difficulties in modeling the laminar-to-turbulent transition and laminar bubble, as also discussed in [16,20,21,22]. Although the difference between the experimental and simulated drag coefficients is relatively small in this case, further improvement could be achieved by exploring more suitable turbulence models or implementing higher-fidelity models.

4. Conclusions

This study presents the first rigorous experimental and numerical evaluation of the aerodynamic characteristics of Aurel Persu’s 1922 streamlined automobile. The combined approach using wind tunnel testing, PIV measurements and CFD simulations provides comprehensive insights into the vehicle’s flow characteristics.

Key findings include the following:

• The measured drag coefficient of C_D = 0.364 is significantly higher than the commonly cited value of 0.28, demonstrating the importance of experimental validation.
• Flow separation occurs shortly after the windshield, creating a substantial recirculation zone behind the cabin that extends over 25% of the vehicle length.
• CFD simulations (C_D = 0.353) show good agreement with experimental results, with the small discrepancy attributed to delayed separation prediction by the RANS model.
• The vehicle’s aerodynamic performance is limited by suboptimal front geometry and roofline design.

While the Persu’s car represents an important early attempt at automotive streamlining, the results indicate that its aerodynamic efficiency falls short of modern streamlined vehicles. The methodology developed in this study provides a validated framework for analyzing historical automotive designs and can inform future aerodynamic optimization efforts.