Dimensional Synthesis of a Pulse-Type Adjustable Speed Drive Based on a Six-Bar Watt II Linkage ^†

Abstract

This paper presents a method for dimensional synthesis of a pulse-type adjustable speed mechanical drive, realized through a Watt II six-bar linkage combined with an overrunning clutch. The goal is to achieve a transmission ratio that varies smoothly and linearly by adjusting the angle of a control lever, while meeting kinematic, geometric, and force constraints. The kinematic characteristics are derived analytically using vector-loop equations, enabling comparison with a predefined linear reference function. An optimization problem is formulated to minimize the maximum deviation between the actual and reference output angles across the entire operating interval. The solution employs a metaheuristic algorithm for global search followed by a local refinement phase. Three optimization scenarios are analyzed, each with different levels of design freedom regarding the parameters defining the linear reference function. The results demonstrate a clear trade-off between accuracy and functional tunability, highlighting the most effective balance for practical applications. This approach can be used for designing mechanical drives with adjustable speed features and can be applied to other complex linkage systems.

1. Introduction

The pulse-type adjustable speed drives transfer power from the driving link to the driven link in discrete portions. This is achieved by a link that performs continuous rotary motion, which is converted into intermittent unidirectional rotary motion of the output link through a Watt II six-bar linkage and an overrunning clutch [1,2]. Their primary use is in systems that need to regulate the output link’s speed continuously within a specific range. The main drawback of this drive is the unevenness of the output motion.

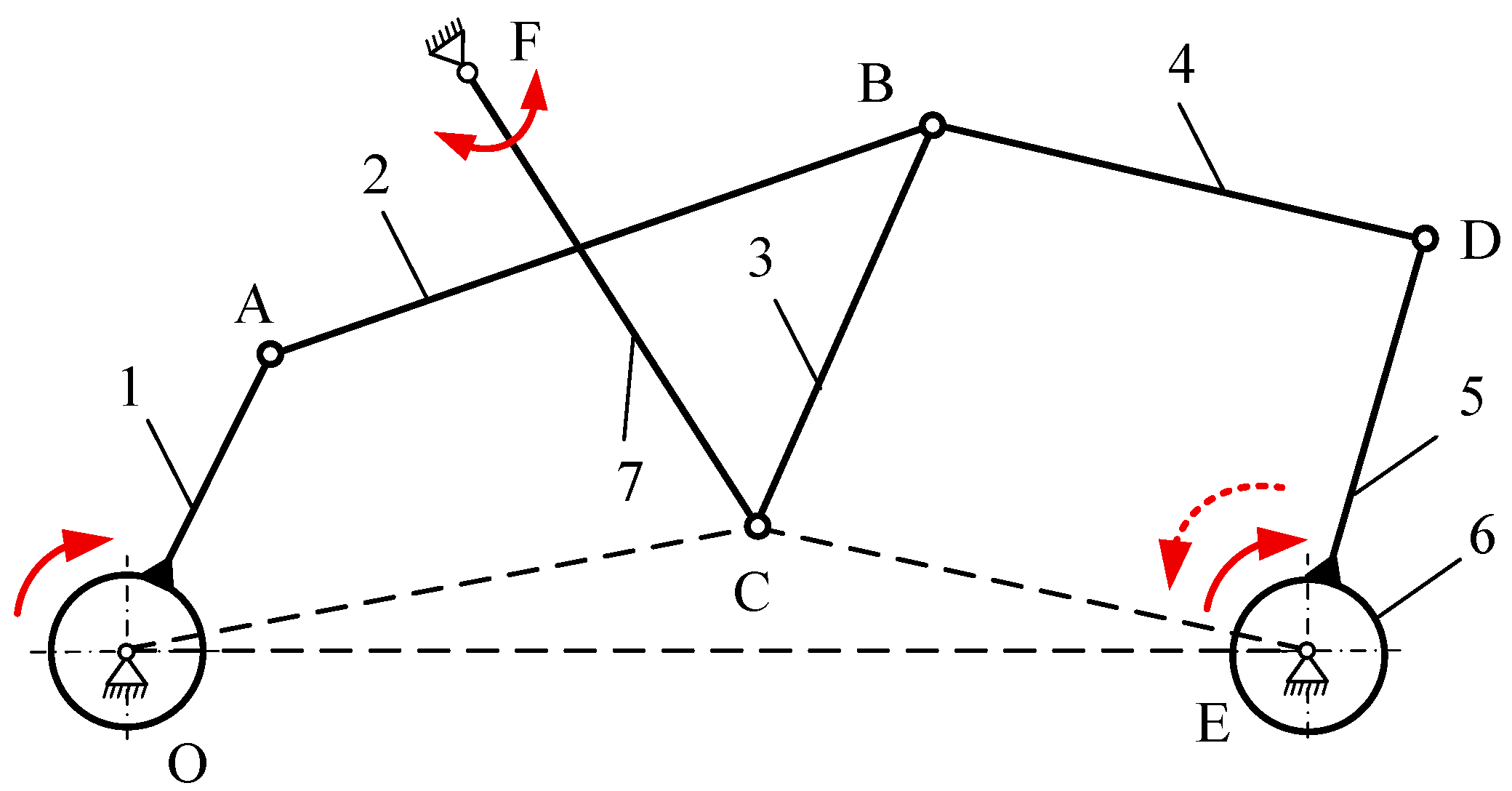
Figure 1 shows the geometric arrangement of this drive [1]. Two four-link loops connected in series form the six-bar Watt II type linkage. The first loop is driven by crank 1, which is rigidly attached to the input shaft with an axis aligned with the hinge O center. The motion is transmitted through link 2 to the output link 3, which drives the second loop. Link 4 transmits movement to link 5, the output link of the second loop, which is rigidly connected to the output shaft mounted on an overrunning clutch. The output link 5 oscillates after one revolution of the input shaft.

When the mechanism rotates forward, the clutch engages and transmits power to the output. When reversed, the clutch overruns and does not transmit torque. Adjusting the transmission ratio of the six-bar linkage is achieved by turning the control lever FC. This shifts the position of point C and, consequently, alters the mechanism’s geometry. To reduce the unevenness of the rotation of the output shaft, the design includes multiple parallel six-bar linkages of the same type, each driven by cranks set out of phase [1]. For example, four mechanisms will have a phase shift of 90°.

Research on the synthesis of pulse-type adjustable speed drives is limited despite their widespread manufacturing [3]. Tsonov’s PhD thesis [1] focuses on a series of tests of pulse-type adjustable speed drives and proposes a method for synthesizing the generating mechanism. References [4,5] analyze and synthesize a variable-speed transmission that employs an adjustable six-bar linkage to transform constant-speed rotations into controllable oscillations of the output link, complemented by an overrunning clutch. In [6], an analytical approach and a developed program were used to design a planar six-bar linkage with an adjustable coupler length to achieve multiple output motions. The authors of [7] introduce an innovative approach based on the cuckoo optimization method for the dimensional synthesis of an adjustable six-bar linkage, utilizing crank-rocker and slider-crank mechanisms. The study in [8], which holds high practical significance, details a method and software for multivariate design of impulse variators with an almost infinite range of transmission ratios, intended for use in main gears and steering systems of tracked vehicles.

The primary aim of the dimensional synthesis of the six-bar linkage under consideration is to determine the link dimensions and the positions of the suspension points needed to produce the desired mechanism motion. The problem is mathematically complex due to many variables and nonlinear relationships among them, making traditional analytical methods difficult to apply. Framing the synthesis as an optimization problem allows for increasing the problem’s dimensionality and finding the global extremum while respecting the geometric, kinematic, and force constraints. Modern metaheuristic methods are an effective tool for solving high-dimensional optimization problems with relatively small computational resources [9]. Extensive literature demonstrates the use of these methods for solving issues in mechanism analysis and synthesis. In [10], Bulatović & Đorđević utilize the Differential Evolution (DE) method for path generation through a six-link mechanism, achieving high accuracy. A similar approach is used in [11], where DE is combined with the geometric centroid of the positions to synthesize six-bar mechanisms with dwell and double dwell motion. Villegas et al. [12] propose a two-step Genetic Algorithms (GA) based approach for a six-bar linkage generating function with imposed dynamic constraints. A GA is also used in [13] for the synthesis of a Stephenson I six-bar mechanism for path following with minimal position error. In [14], an advanced evolutionary algorithm called MUMSA was developed and applied to both four- and six-bar linkages, demonstrating competitive results compared to other strategies. In paper [15], a Stephenson III six-link mechanism was synthesized using Particle Swarm Optimization (PSO), achieving reduced trajectory error along a complex path. The authors of [16] applied PSO to size a Watt II mechanism, considering both kinematic and dynamic criteria. In a recent paper [17], Nikitović et al. combined DE with a marine predator algorithm and synthesized a four-bar mechanism for path generation.

This paper aims to develop a method for a dimensional synthesis of a pulse-type adjustable-speed drive employing a six-bar Watt II linkage. The proposed design enables a continuously adjustable (stepless) transmission ratio, controlled through the angular displacement of a control lever, such that the resulting transmission ratio function closely approximates a predefined linear reference within a specified operating interval. The synthesis process is constrained by kinematic, geometric, and force-related constraints, and is formulated as an optimization problem. The objective is to minimize the deviation between the actual and target transmission characteristics, with the solution obtained through a metaheuristic optimization algorithm.

2. Materials and Methods

2.1. Kinematic Analysis of the Mechanism

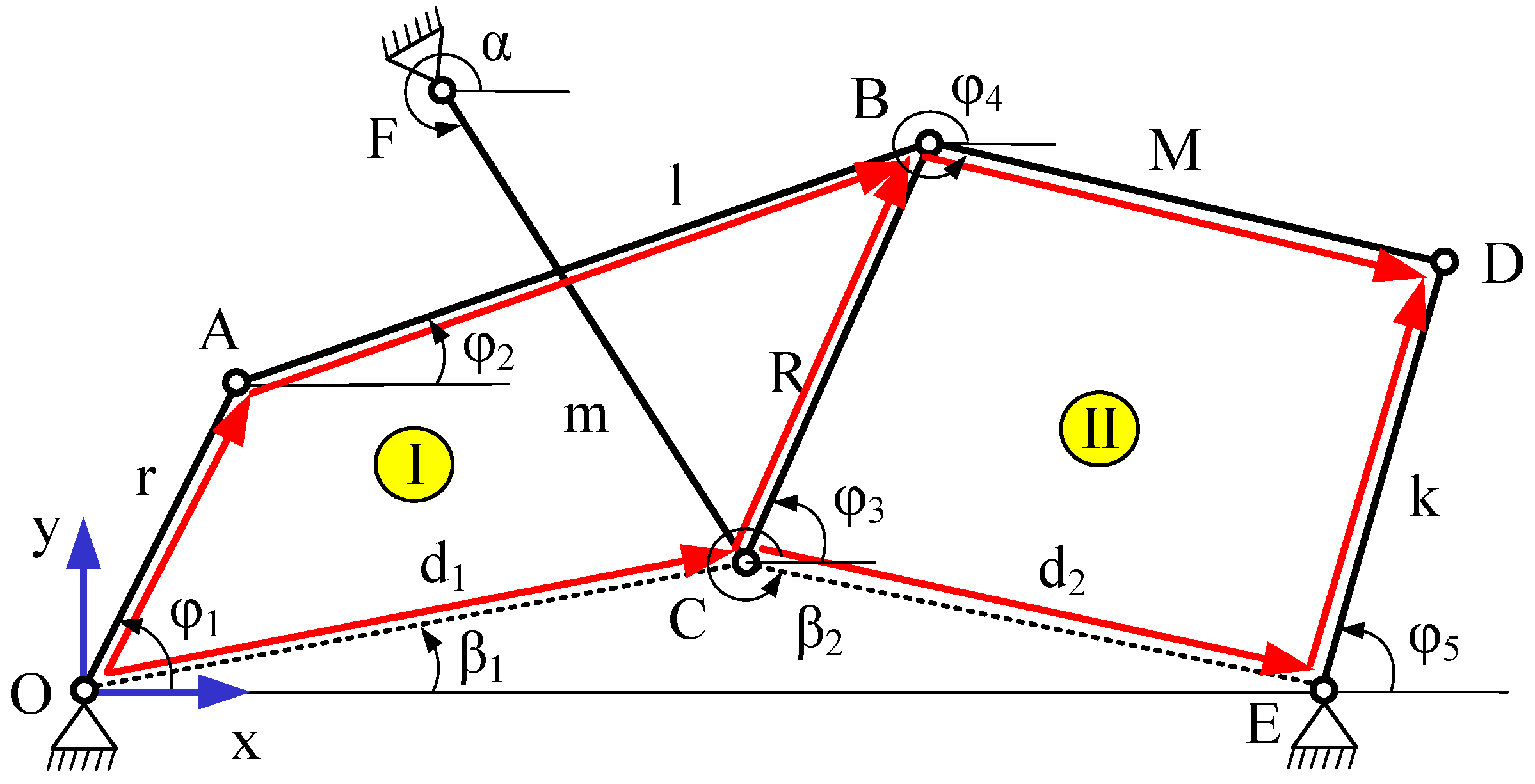
The closed vector contour method is used to conduct kinematic analysis of the mechanism, which will be utilized to develop the optimization model. The mechanism’s kinematic diagram is presented in Figure 2. The inclination of each link is measured relative to the horizontal axis, with the counterclockwise direction considered positive.

The analytical position equations of the two vector contours [18], based on the assumed directions of the vectors, are formulated as follows:

For contour I:

$$OA+AB-OC-CB=0$$

(1)

For contour II:

$$CB+BD-CE-ED=0$$

(2)

The position functions of the two contours can be determined by projecting their equations onto the coordinate axes and solving them analytically as a system of equations.

For contour I:

$${\phi }_3=\mathrm{atan}2\left(\sin {\phi }_3,\cos {\phi }_3\right)$$

(3)

where $\cos {\phi }_3={\displaystyle \frac{-A_I{C}_I+B_I\sqrt{A_I^2+B_I^2-C_I^2}}{A_I^2+B_I^2}}$, $\sin {\phi }_3=\sqrt{1-{\cos }^2{\phi }_3}$, $x_C=x_F+m\cos \alpha$, $y_C=y_F+m\sin \alpha$, ${\beta }_1=\mathrm{atan}2\left(x_C,y_C\right)$, $d_1=\sqrt{x_C^2+y_C^2}$, $A_I=2R\left(r\cos {\phi }_1-d_1\cos {\beta }_1\right)$, $B_I=2R\left(r\sin {\phi }_1-d_1\sin {\beta }_1\right)$,$C_I=l^2-d_1^2-r^2-R^2+2d_{1}r\cos \left({\beta }_1-{\phi }_1\right)$.

For contour II:

$${\phi }_5=\mathrm{atan}2\left(\sin {\phi }_5,\cos {\phi }_5\right)$$

(4)

where $\cos {\phi }_5={\displaystyle \frac{-A_{II}{C}_{II}+B_{II}\sqrt{A_{II}^2+B_{II}^2-C_{II}^2}}{A_{II}^2+B_{II}^2}}$, $\sin {\phi }_5=\sqrt{1-{\cos }^2{\phi }_5}$, ${\beta }_2=\mathrm{atan}2\left(x_E-x_C,y_E-y_C\right)$, $d_2=\sqrt{{\left(x_E-x_C\right)}^2+{\left(y_E-y_C\right)}^2}$, $A_{II}=2k\left(R\cos {\phi }_3-d_2\cos {\beta }_2\right)$, $B_{II}=2k\left(R\sin {\phi }_3-d_2\sin {\beta }_2\right)$, $C_{II}=M^2-d_2^2-k^2-R^2+2d_{2}R\cos \left({\beta }_2-{\phi }_3\right)$.

In the expressions for $\cos {\phi }_3$ and $\cos {\phi }_5$ the signs before the radicals are chosen to implement the proper contour assembly schemes.

The following relationship defines the transmission ratio of the linkage:

$${\displaystyle \frac{\partial {\phi }_5}{\partial {\phi }_1}}={\displaystyle \frac{r}{k}}{\displaystyle \frac{\sin \left({\phi }_4-{\phi }_3\right)}{\sin \left({\phi }_4-{\phi }_5\right)}}{\displaystyle \frac{\sin \left({\phi }_2-{\phi }_1\right)}{\sin \left({\phi }_2-{\phi }_3\right)}}$$

(5)

where ${\phi }_2=\mathrm{atan}2\left(\sin {\phi }_2,\cos {\phi }_2\right)$, $\cos {\phi }_2=\left(d_1\cos {\beta }_1+R\cos {\phi }_3-r\cos {\phi }_1\right)/l$, $\sin {\phi }_2=\left(d_1\sin {\beta }_1+R\sin {\phi }_3-r\sin {\phi }_1\right)/l$; ${\phi }_4=\mathrm{atan}2\left(\sin {\phi }_4,\cos {\phi }_4\right)$, $\cos {\phi }_4=\left(d_2\cos {\beta }_2+k\cos {\phi }_5-R\cos {\phi }_3\right)/M$, $\sin {\phi }_4=\left(d_2\sin {\beta }_2+k\sin {\phi }_5-R\sin {\phi }_3\right)/M$.

2.2. Defining the Optimization Problem

The main goal of the mechanism’s dimensional synthesis is to determine the sizes of the links and the locations of their attachment points to achieve a linear variation in the transmission ratio within specific limits by adjusting the angular displacement α of the control lever FC (see Figure 2).

The reference linear function of the linkage transmission ratio $\partial {\phi }_5^{ref}/\partial {\phi }_1$ includes a constant u and a variable $\left(\alpha -{\alpha }_0\right)v$ parts [1]:

$${\displaystyle \frac{\partial {\phi }_5^{ref}}{\partial {\phi }_1}}=u+\left(\alpha -{\alpha }_0\right)v$$

(6)

where u denotes the constant transmission ratio of the mechanism, v denotes the proportionality coefficient, and $\alpha$ represents the current value of the control lever’s angular displacement, which varies within the limits $[{\alpha }_0, {\alpha }_{\max }]$, where α₀ and α_max are the initial and maximum values of the angle. With this definition, the transmission ratio of the mechanism will change within the limits $\left[u, u+\left({\alpha }_{\max }-{\alpha }_0\right)v\right]$.

The reference angle function of the output link ${\phi }_5^{ref}$ is derived by integrating (6):

$${\phi }_5^{ref}=\left({\phi }_1-{\phi }_{10}\right)\left(u+\left(\alpha -{\alpha }_0\right)v\right)+{\phi }_{50}$$

(7)

where ${\phi }_{10}$ and ${\phi }_{50}$ are integration constants corresponding to the initial values of the angles of input and output links, respectively. According to (7), at a fixed value of the angle α, the angle of the output link ${\phi }_5^{ref}$ is directly proportional to the angle of the input link ${\phi }_1$. This shows that within the operating range of ${\phi }_1\in [{\phi }_{10}, {\phi }_{1\max }]$, where ${\phi }_{1\max }$ is the upper boundary of the range, the linear relationship between the rotation angles of the input and output links is maintained. Therefore, the mechanism serves as a function generator within the operating interval.

Let $\Delta {\phi }_5$ denote the difference between the actual angle ${\phi }_5$ of the output link, obtained from the kinematic model (3) and (4), and the reference angle ${\phi }_5^{ref}$:

$$\Delta {\phi }_5={\phi }_5-{\phi }_5^{ref}$$

(8)

Considering that $\Delta {\phi }_5$ has a variable value depending on the current values of the angles ${\phi }_1$ and $\alpha$, the objective function $\Delta {\phi }_5^{*}$ of the optimization problem is defined as follows [1]:

$$\Delta {\phi }_5^{*}=\min \left\{\underset{\begin{array}{l}{\phi }_1\in \left[{\phi }_{10},{\phi }_{1\max }\right]\\ \alpha \in \left[{\alpha }_0,{\alpha }_{\max }\right]\end{array}}{\max }\left|\Delta {\phi }_5\right|\right\}$$

(9)

This function calculates the minimum of the maximum deviation [19] of the actual angle ${\phi }_5$ from the reference angle ${\phi }_5^{ref}$ within the range of change of the input link angle ${\phi }_1\in [{\phi }_{10}, {\phi }_{1\max }]$ and the range of angular displacement of the control lever $\alpha \in [{\alpha }_0, {\alpha }_{\max }]$. The minimum of the maximum deviation occurs at a specific combination of angles $\left({\phi }_1^w,{\alpha }^w\right)$. This combination represents the worst case.

The objective function should be optimized subject to the following constraints, which are checked for each combination of φ₁ and α within their definition intervals:

• For the input link length r to make a full rotation, Grashof’s condition [18] must be satisfied:

  $$2\left[\min \left(r,l,R,d_1\right)+\max \left(r,l,R,d_1\right)\right]<r+l+R+d_1$$

  (10)
• In addition to Grashof’s condition, it should be ensured that the crank r is the shortest link in the first contour:

  $$r<\min \left(l,R,d_1\right)$$

  (11)
• Transmission angles [18] ${\gamma }_I$ and ${\gamma }_{II}$ for both contours (see Figure 2), respectively, must be limited:

$${\gamma }_I=\left|{90}^0-\arccos {\displaystyle \frac{AB\cdot BC}{‖AB‖‖BC‖}}\right|\le {\gamma }_{\lim }$$

(12)

$${\gamma }_{II}=\left|{90}^0-\arccos {\displaystyle \frac{BD\cdot ED}{‖BD‖‖ED‖}}\right|\le {\gamma }_{\lim }$$

(13)

where ${\gamma }_{\lim }$ is the maximum allowable value of the angles;

4.

Geometric conditions required for the mechanism’s existence (see (3) and (4)):

$$A_I^2+B_I^2-C_I^2\ge 0$$

(14)

$$A_{II}^2+B_{II}^2-C_{II}^2\ge 0$$

(15)

5.

Design variable ranges:

$$x_{LB}\le x\le x_{UB}$$

(16)

where x denotes the vector of design variables:

$$x=\left[\begin{array}{ccccccccc}r& l& R& m& M& k& x_F& y_F& x_E\end{array}\right]$$

(17)

and x_LB and y_LB are vectors containing the numerical values of the lower and upper bounds of the design variables.

2.3. Solving the Optimization Problem

The PSO algorithm, known for its simple implementation, reliance on a few parameters, and fast convergence [9], is employed to solve the optimization problem. To prevent PSO from becoming stuck in a local optimum, it is combined with a local gradient method after the global phase is completed to refine the found minimum. Optimization is performed within the following ranges of angles changes -${\phi }_1\in [{90}^0,{180}^0]$ and $\alpha \in [{320}^0, {350}^0]$, also it is accepted ${\phi }_{50}={90}^0$. A step size of 0.5⁰ is used to discretize the range of change of ${\phi }_1$ and $\alpha$, creating a grid of 180 × 60 points, in the nodes of which the objective function (9) is calculated. Numerical tests have demonstrated that this grid density offers a good balance between result accuracy and calculation time. Initially, a swarm of 60 particles was generated.

Three optimization scenarios were evaluated to assist the design process and analyze how different parameters influence the mechanism’s kinematic properties.

Scenario 1. The design variables vector only includes the geometric parameters of the mechanism, as in (17). The linkage transmission ratio (7) is set with the following constant numerical values of the coefficients: u = 0.2 and v = 0.005. These values allow for stepless change in the transmission ratio within the interval $\left[0.2, 0.35\right]$;

Scenario 2. The design variables vector is expanded by adding u as an additional optimization variable, and the value of v is assumed to be constant at v = 0.005;

Scenario 3. Both coefficients u and v are included as optimization variables in the design variable vector.

For all three scenarios, it is accepted that ${\gamma }_{\lim }={50}^0$.

Table 1. Optimization results.

Parameter	Scenario 1			Scenario 2			Scenario 3
	LB	UB	Optimal Value	LB	UB	Optimal Value	LB	UB	Optimal Value
r, mm	10	50	34.3	10	50	26.3	10	50	18.4
l, mm	40	250	191.0	40	250	95.1	40	250	145.8
R, mm	50	140	109.1	50	140	131.2	50	140	104.4
m, mm	40	150	92.9	40	150	52.1	40	150	40.0
M, mm	50	180	155.3	50	180	122.1	50	180	170.8
k, mm	50	180	124.4	50	180	98.7	50	180	141.3
xF, mm	−50	100	41.8	−50	100	−9.2	−50	100	67.0
yF, mm	−50	140	32.5	−50	140	−40.7	−50	140	−7.1
xE, mm	200	600	330.5	200	600	203.5	200	600	290.5
u	0.2	0.2	0.2	0.1	0.3	0.227	0.18	0.22	0.115
v	0.005	0.005	0.005	0.005	0.005	0.005	−0.007	0.007	0.0008
$\Delta {\phi }_5^{*}$	1.8110			1.2430			0.5150
$\left({\phi }_1^w,{\alpha }^w\right)$	(1800, 3380)			(155.50, 3200)			(146.50, 3200)
E × 100%	≈7%			≈6.03%			≈4.95%

summarizes the optimization results for the three scenarios and shows: (1) Numerical values of the lower LB and upper UB bounds of the design variables; (2) Optimal values of the design variables; (3) Value of the objective function $\Delta {\phi }_5^{*}$; (4) Coordinates $\left({\phi }_1^w,{\alpha }^w\right)$ of the grid node where the maximum deviation occurs. All constraints on the objective function are satisfied in the three scenarios.

To evaluate the relative significance of the achieved deviation, the dimensionless index E is computed. It equals the maximum deviation $\Delta {\phi }_5^{*}$ divided by the achieved variation range of the reference angle ${\phi }_5^{ref}$ (read from Figure 6). The values calculated are shown in the last row of Table 1.

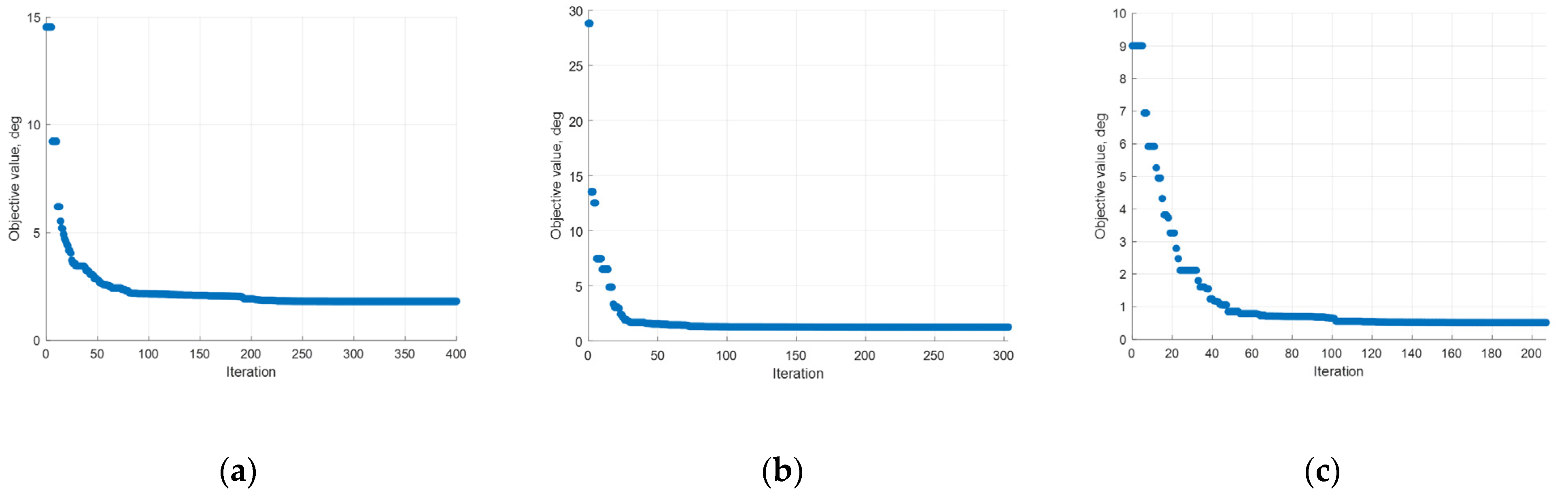
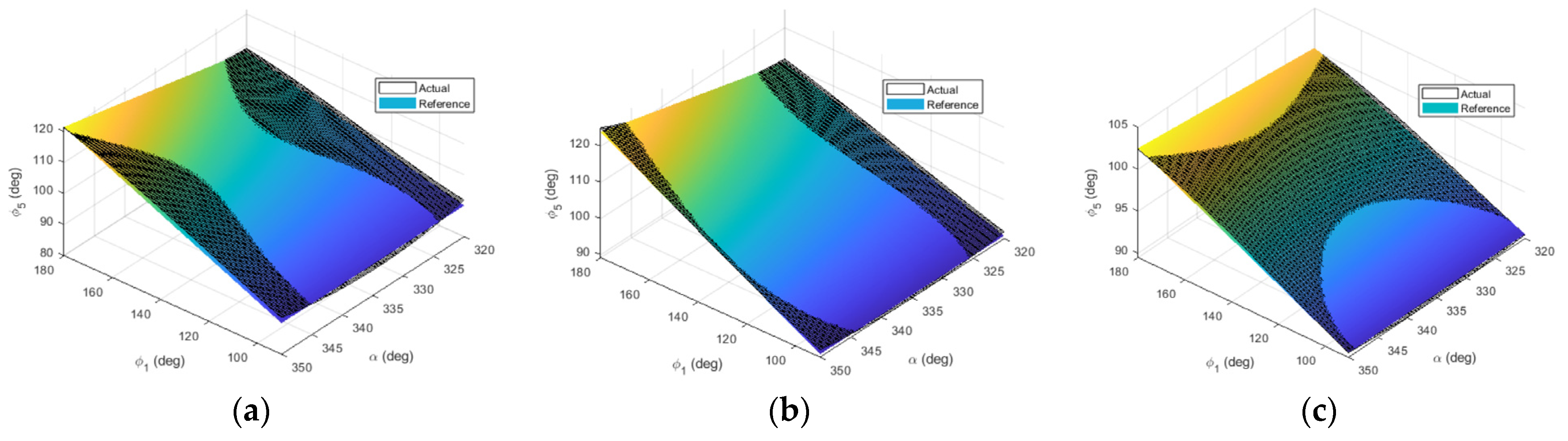
Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8 display the kinematic characteristics of the optimal mechanism across the three different scenarios. Figure 3 presents objective function convergence curves, indicating that the optimal solution is achieved in 150–200 iterations. Figure 4 shows 3D plots of the actual ${\phi }_5$ and reference ${\phi }_5^{ref}$ angles, plotted as a function of φ₁ and α. 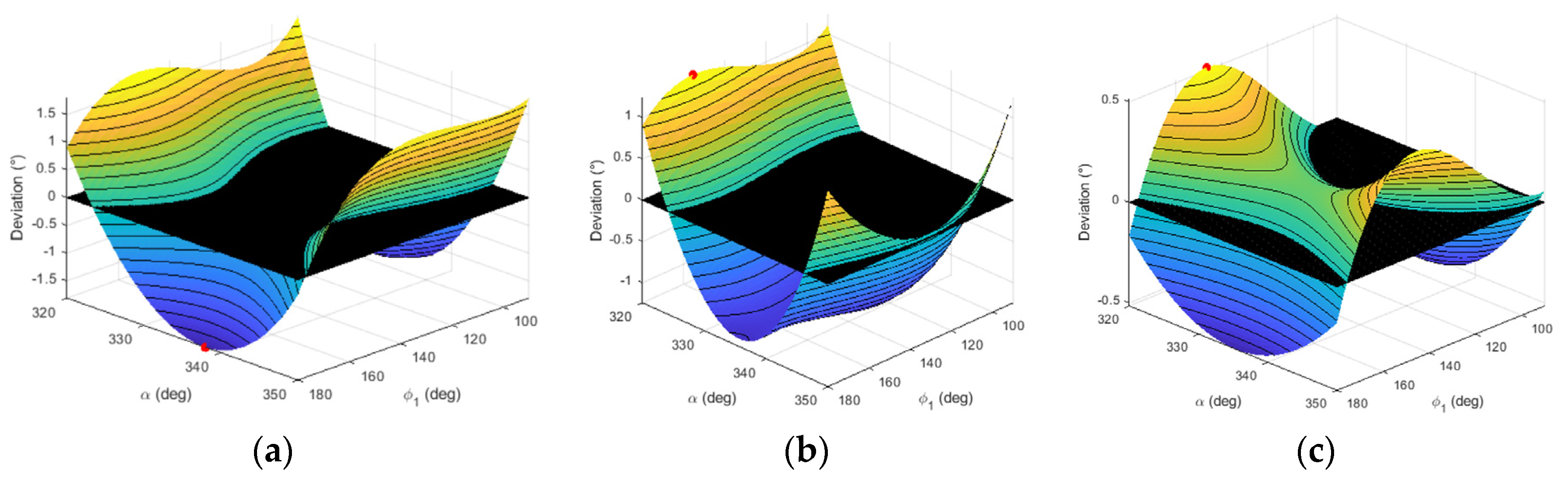In Figure 5 3D plots of the deviation $\Delta {\phi }_5={\phi }_5-{\phi }_5^{ref}$ are shown. The red points indicate the absolute maximum values of the function. 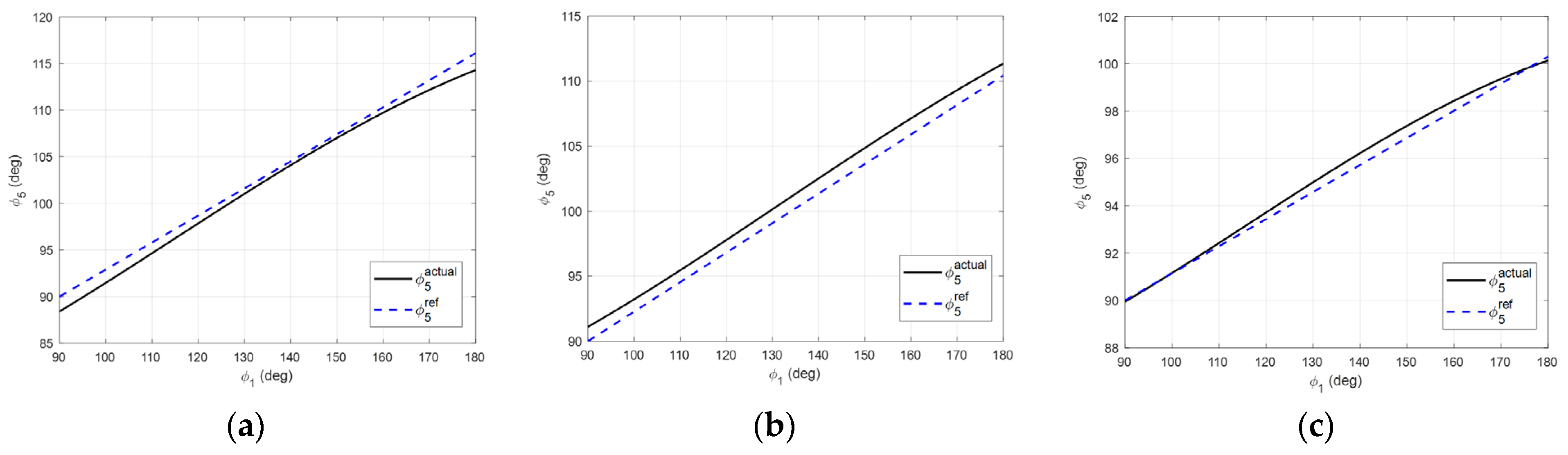Figure 6 shows the actual ${\phi }_5$ and reference ${\phi }_5^{ref}$ angles, constructed at the value $\alpha ={\alpha }^w$(position of the control lever for the worst case). 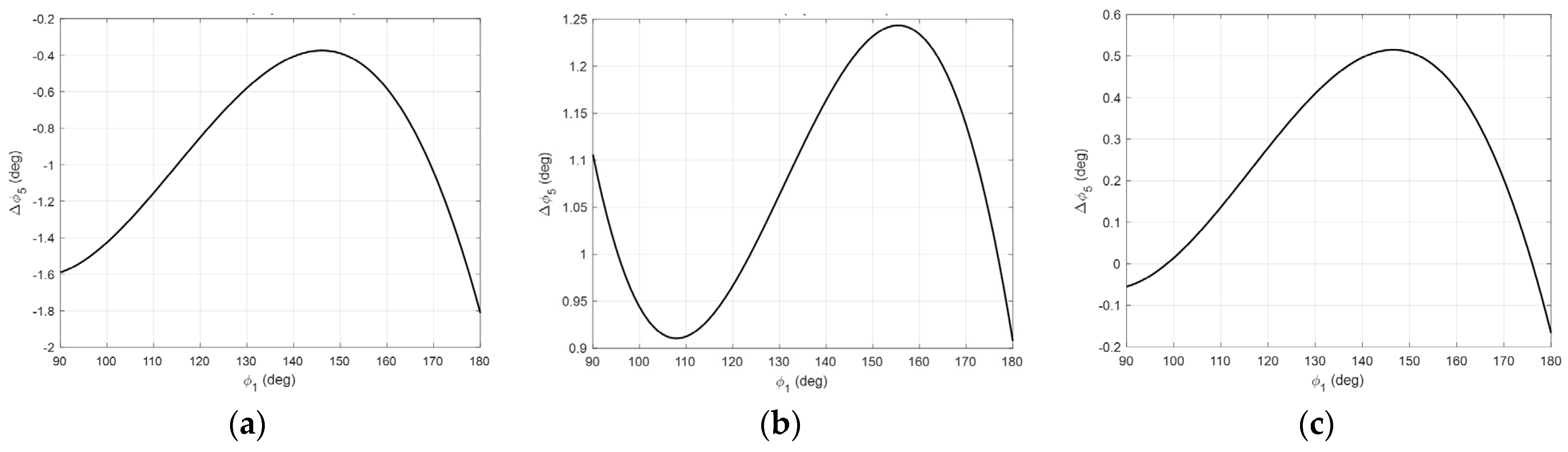In the considered range, the real curve is close to a straight line, with some deviation between them, which is visualized in Figure 7, depicting $\Delta {\phi }_5=f\left({\phi }_1\right)$ for $\alpha ={\alpha }^w$. 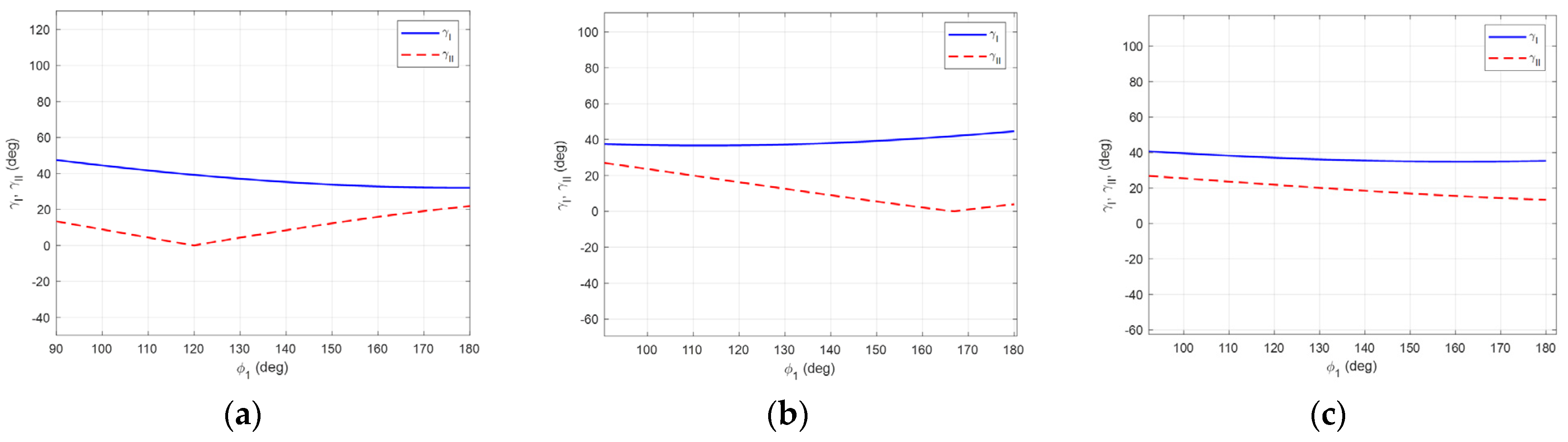Figure 8 shows plots of the deviation angles (12) and (13), whose values are smaller than ${\gamma }_{\lim }$ for the considered range.

3. Discussion

The results from solving the optimization problem for the dimensional synthesis of the six-bar linkage allow for a detailed analysis and discussion of the outcomes and the effectiveness of the selected approaches.

The optimal values of the design variables (see Table 1) across all three scenarios ensure high accuracy of the required linear adjustable characteristic of the transmission ratio within the specified rotation limits. The obtained value of the objective function (9), which measures the minimum of the maximum deviation from the reference function, indicates a substantial success in meeting the set task. This numerical value reflects the precision with which the linkage achieves the desired linear relationship between input and output link motions as the control angle varies. In all cases, the low values demonstrate good alignment between the mechanism’s actual and intended behavior.

Also, for each scenario, specific combinations of angles $\left({\phi }_1^w,{\alpha }^w\right)$ were identified where the deviation between the simulated and reference functions reaches its maximum. This critical case represents the least favorable operating condition for the mechanism and requires close attention. The maximum deviation at this angle likely results from the combination of geometric and kinematic constraints related to the specific position of the mechanism, where the transmission angles are least favorable, and the kinematic movement conditions are hardest to execute. Having a critical case enables the mechanism to be improved by readjusting constraints, adding additional constraints, or fine-tuning parameters near this critical angle. Despite the existence of such a critical case, the overall evaluation of the result remains positive, as the synthesis successfully achieves the set goals—linearity and stepless regulation of the transmission ratio within the allowable deviation.

Solving the problem, based on the first optimization scenario, is the most preferable and provides the highest engineering value, because in this case, the constant u and the variable $\left(\alpha -{\alpha }_0\right)v$ parts of the transmission ratio (6) are intentionally set by the user (in this scenario u = 0.2 and v = 0.005). This enables designing an adjustable speed drive with limits precisely set by the designer for changing the angular velocity of the output link, although it results in a larger error ($\Delta {\phi }_5^{*}={1.811}^0$, E ≈ 7%) compared to the other two scenarios.

The natural extension of the optimization problem to improve the value of the objective function is to include the constant transmission ratio u in the vector of design variables. The optimal value of u should then be calculated, just as was performed in Scenario 2. In this case, the value of v remains fixed at v = 0.005 to preserve the required range of change in the output angular velocity. The value of the objective function obtained $\Delta {\phi }_5^{*}={1.243}^0$ is improved by about 1/3 compared to Scenario 1, and E ≈ 6.03%. This approach can better approximate the reference function, but it reduces the designer’s control over the constant part of the transmission ratio u.

In Scenario 3, the lowest value of the objective function ($\Delta {\phi }_5^{*}={0.515}^0$ and E ≈ 4.95%) is reached through the simultaneous optimization of u and v. The many conducted numerical experiments show this is an impractical solution, because the obtained optimal value of v always takes a small value, close to 0 (in this case v = 0.0008 is obtained). This significantly limits the adjustment range of the output angular velocity, turning the mechanism into a device with a constant output angular velocity and minimal adjustment capabilities. From an application standpoint, even with a minor error, this scenario is the least favorable from a practical perspective.

4. Conclusions

This paper presents an optimization-driven process for the dimensional synthesis of a pulse-type adjustable speed drive employing a Watt II six-bar linkage. The problem is formulated as a constrained optimization task and solved with the Particle Swarm Optimization method, ensuring the transmission ratio remains within specified bounds while accurately following a designated linear reference curve.

The optimization using PSO consistently identifies the optimal geometric parameters of the mechanism under combined kinematic, geometric, and force constraints. These results demonstrate that metaheuristic methods are effective for highly nonlinear, high-dimensional mechanism synthesis problems that challenge traditional analytical techniques. A major advantage of the proposed workflow is its complete automation. The design cycles are shortened, and designers can quickly perform “what-if” studies to compare different configurations, resulting in more competitive mechanical systems.

The results show that Scenario 1, which includes only the geometrical parameters of the mechanism, provides the best balance between closely approximating the transmission ratio reference function and the user’s ability to control the output kinematic characteristics. However, despite the minimal error in Scenario 3, the outcome results in an almost constant transmission ratio and limited adjustability, which conflicts with the primary goal of adjustable speed drives.

Future developments will include dynamic criteria, multi-objective optimization, and sensitivity analysis to improve the model further. The method can be easily adapted to synthesize other types of mechanisms, significantly expanding its usefulness.