Analytical Subdomain Model for Double-Stator Permanent Magnet Synchronous Machine with Surface-Mounted Radial Magnetization ^†

Abstract

This paper proposes an analytical subdomain model for predicting magnetic field distributions in a three-phase double-stator permanent magnet synchronous machine (DS-PMSM) during open-circuit and on-load conditions. The geometric structure of DS-PMSM is quite challenging since the stator cores are located in the outer and inner parts of the motor, while the rotor magnets are placed between these two stators. Parameters that influence the motor performance in DS-PMSM include stator outer radius, stator inner radius, magnet thickness, magnet arc, slot opening, outer and inner airgap thickness and the number of winding turns. The analytical subdomain model proposed in this paper, which can accurately predict the performances of DS-PMSM with less computational time, has an excellent advantage as a rapid design tool. The model is initially generated using the separation of variables technique in four subdomains, namely, outer airgap, outer magnet, inner magnet, and inner airgap, based on Laplace’s and Poisson’s equations in polar coordinates. The field solutions in each subdomain are derived by applying the appropriate boundary and interface conditions. Furthermore, finite element analysis (FEA) is used to validate the analytical results in fractional DS-PMSM with a different number of slots between outer and inner stators and a non-overlapping winding configuration. The electromagnetic performances that have been evaluated are the slotted airgap flux density, back-emf and output torque. The results demonstrate that the proposed analytical model is able to predict the magnetic field distributions accurately in DS-PMSM.

1. Introduction

Double-stator permanent magnet synchronous machines (DS-PMSM) have recently been the subject of extensive research due to advantages such as higher torque and power density when compared to conventional single-stator PMSM [1,2,3]. The double-stator PMSM is used for Electric Vehicles (EVs) and is also proposed for dual-channel magnetically integrated charger operations [1]. In [2], the double-stator was developed to reduce manufacturing costs in machine constructions based on the relative positioning of both stator slots. The DS-PMSM is applied to a wind power generation system in [3] with the machine deploying two spatially independent stators for cooling.

In general, the ratio of both stator slot numbers to the rotor pole number in DS-PMSM is fractional and as a result, the machine incorporates a high winding factor [4]. Typically, numerical methods such as the finite element method (FEM) in 2D and 3D have been intensively used for designing and determining the optimal configuration of DS-PMSM before proceeding to fabrication and manufacture. This motor’s construction and design choices involve numerous parameters. Manually varying the important parameters in machine constructions, on the other hand, will require a longer computational time, and therefore, is not practical for achieving the best motor performance [5,6].

To address this issue, an analytical subdomain model provides a viable and faster solution for designing DS-PMSMs. In this regard, this paper develops an analytical sub-domain model for three-phase DS-PMSM with different numbers of slots between outer and inner stators, where the slot-to-pole combination for the outer part is 12-slot/10-pole and for the inner part is 9-slot/10-pole.

2. Motor Geometry

The developed model of the three-phase DS-PMSM, which consists of a 12-slot outer stator, a 10-pole rotor, and a 9-slot inner stator, is shown in Figure 1. Surface-mounted permanent magnets (PMs) are used on both the inner and outer surfaces of the rotor core. Non-overlapping double-layer windings are applied for both inner and outer stators. Table 1 displays the motor parameters and dimensions.

Figure 1. Construction of DS-PMSM.

Table 1. Parameters and dimensions of DS-PMSM.

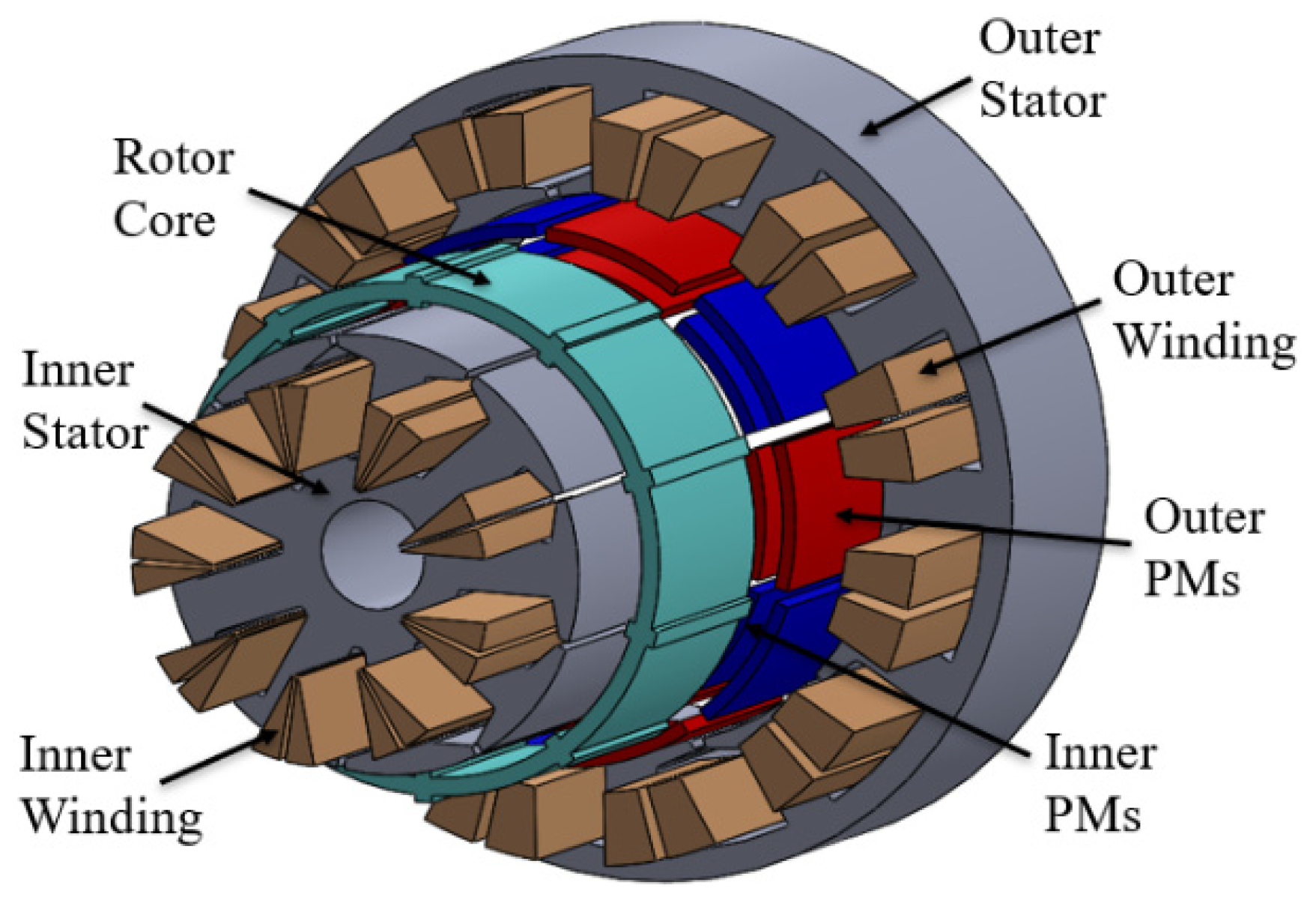
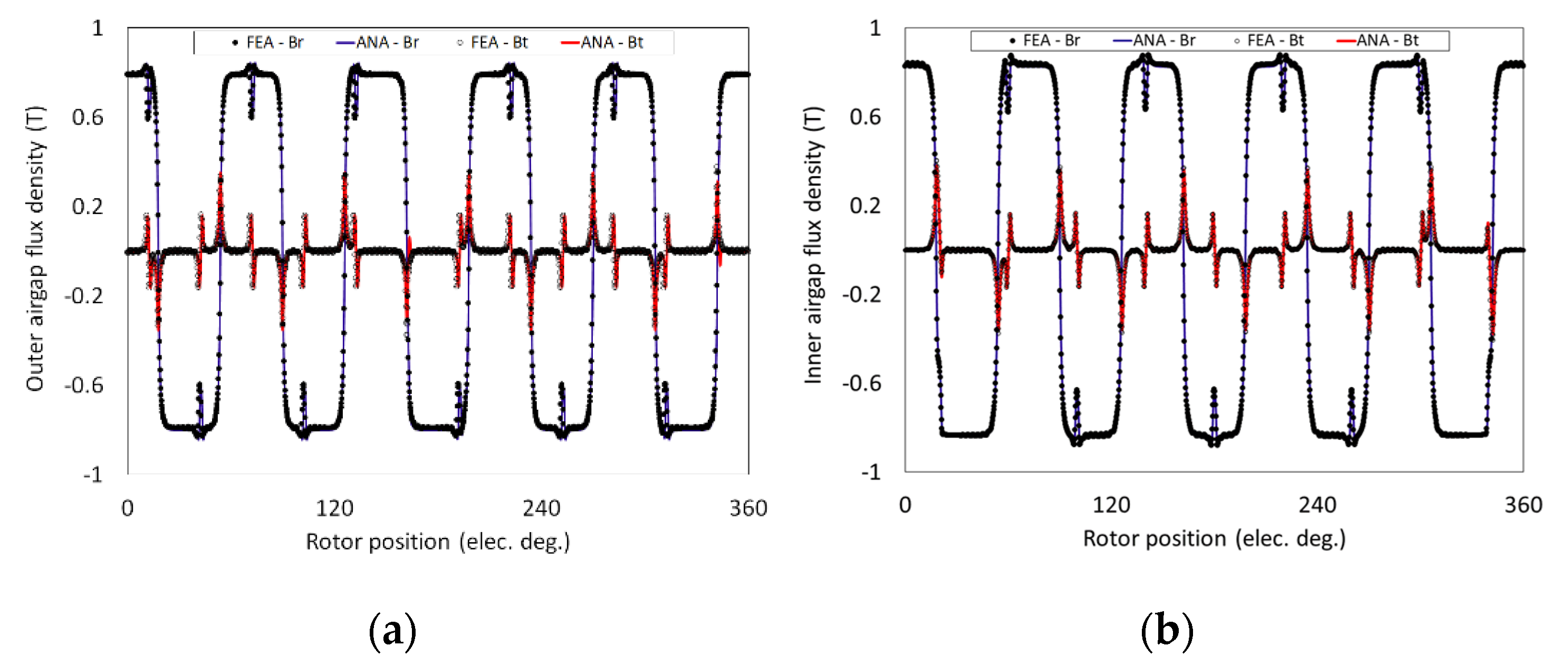
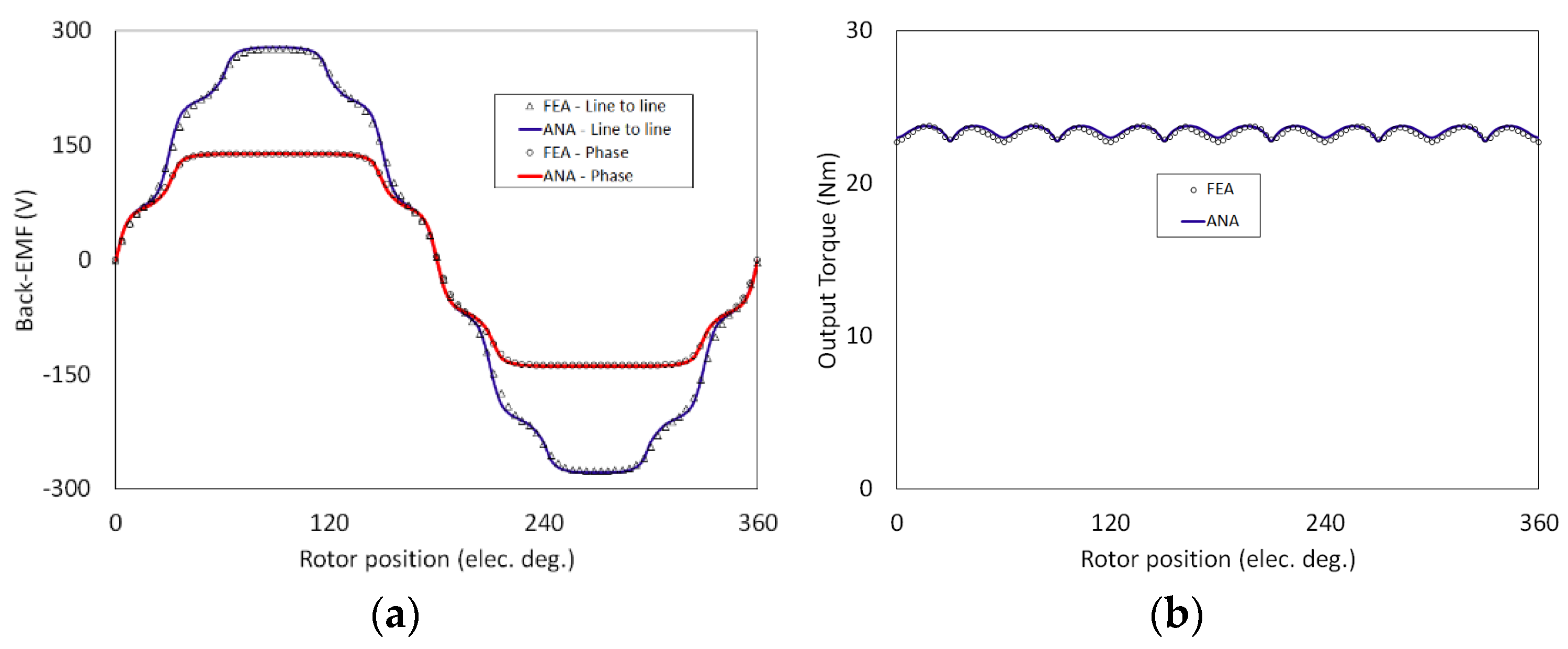
Parameters	Values	Parameters	Values
Outer Stator Slot Number, Nos	12	Stack Length, ls (mm)	40
Inner Stator Slot Number, Nis	9	Outer Airgap Length, log (mm)	1
Rotor Pole Number, 2p	10	Inner Airgap Length, lig (mm)	1
Outer Stator Outer Radius, Roso (mm)	90	Outer Magnet Thickness, hom (mm)	3
Outer Stator Inner Radius, Rosi (mm)	60	Inner Magnet Thickness, him (mm)	3
Inner Stator Outer Radius, Riso (mm)	48	Magnet Remanence, Br (T)	1.12
Inner Stator Inner Radius, Risi (mm)	12	Saturation Flux density, Bmax (T)	1.6
Rotor Outer Radius, Rro (mm)	56	Relative Recoil Permeability, µr	1.05
Rotor Inner Radius, Rri (mm)	52	Rated Speed, rm (rpm)	600
Outer Magnet Radius, Rom (mm)	59	Outer Winding Turns per coil, Noc	114
Inner Magnet Radius, Rim (mm)	49	Inner Winding Turns per coil, Nic	50

3. Analytical Formulations and Field Solutions

The proposed analytical subdomain model in this paper focuses on the double-stator PM machines with two airgaps. The permanent magnets attached at the outer and inner of the rotor core surfaces with radial magnetization pattern. Magnetic vector potential given by either Laplace’s or Poisson’s equations in each subdomain is obtained by the variable separation technique, and the final solutions are solved by applying the boundary and interface conditions. There are four regions in the motor modelling which are outer airgap, outer permanent magnet, inner airgap and inner permanent magnet. Some assumptions are used in formulating the analytical subdomain model such as infinite permeability in the rotor and stator cores; no conductivity in the rotor and stator cores; the eddy current reaction field is neglected; end effect is neglected; and linear magnet properties. By solving the general solutions consisting of Laplacian and Poissonian equations within the boundary conditions from [7,8], the radial and tangential components of flux density in polar coordinates for the slotted DS-PMSM in the outer airgap are described in Equation (1), while for the inner airgap they are given in Equation (2).

$$\begin{gathered} B_{ro}\left(r,\theta \right)={\displaystyle \sum }_{n=1,3,5\dots }^{\infty }\frac{{\mu }_o{M}_n}{{\mu }_r}\frac{np}{{\left(np\right)}^2-1}·\left\{\frac{2{\left(\frac{R_{ro}}{R_{om}}\right)}^{np+1}+\left(np-1\right)-\left(np+1\right){\left(\frac{R_{ro}}{R_{om}}\right)}^{2np}}{\frac{{\mu }_r+1}{{\mu }_r}\left[1-{\left(\frac{R_{ro}}{R_{osi}}\right)}^{2np}\right]-\frac{{\mu }_r-1}{{\mu }_r}\left[{\left(\frac{R_{om}}{R_{osi}}\right)}^{2np}-{\left(\frac{R_{ro}}{R_{om}}\right)}^{2np}\right]}\right\} \\ ·\left[{\left(\frac{r_o}{R_{osi}}\right)}^{np-1}{\left(\frac{R_{om}}{R_{osi}}\right)}^{np+1}+{\left(\frac{R_{om}}{r_o}\right)}^{np+1}\right]·\cos np\theta \end{gathered}$$

(1)

$$\begin{gathered} B_{ri}\left(r,\theta \right)={\displaystyle \sum }_{n=1,3,5\dots }^{\infty }-\frac{{\mu }_o{M}_n}{{\mu }_r}\frac{np}{{\left(np\right)}^2-1}·\left\{\frac{\left(np-1\right){\left(\frac{R_{im}}{R_{ri}}\right)}^{2np}+2{\left(\frac{R_{im}}{R_{ri}}\right)}^{np-1}-\left(np+1\right)}{\frac{{\mu }_r+1}{{\mu }_r}\left[1-{\left(\frac{R_{iso}}{R_{ri}}\right)}^{2np}\right]-\frac{{\mu }_r-1}{{\mu }_r}\left[{\left(\frac{R_{iso}}{R_{im}}\right)}^{2np}-{\left(\frac{R_{im}}{R_{ri}}\right)}^{2np}\right]}\right\} \\ ·\left[{\left(\frac{r_i}{R_{im}}\right)}^{np-1}+{\left(\frac{R_{iso}}{R_{im}}\right)}^{np-1}{\left(\frac{R_{iso}}{r_i}\right)}^{np+1}\right]·\cos np\theta \end{gathered}$$

(2)

where all parameters are referenced in Table 1. Based on flux density distribution in both mid airgaps, the back-emf induced by phase windings and the output torque developed by the DS-PMSM can be analytically investigated and evaluated.

4. Results and Discussion

Finite element analysis (FEA) is frequently used to model and predict the electromagnetic characteristics and performance of electrical machines. The airgap flux density distributions at mid airgaps of the slotted DS-PMSM are calculated analytically and compared with those obtained from FEA, as shown in Figure 2a for outer stator and Figure 2b for inner stator. The phase and line back-emf waveforms are shown in Figure 3a, while the output torque waveforms under sinusoidal current excitations are given in Figure 3b. From the results illustrated in Figure 2 and Figure 3, it is noted that the proposed analytical subdomain model for DS-PMSM in this paper demonstrates an excellent agreement between the analytical results and those obtained from FEA during open circuit and on-load conditions.

Figure 2. Radial and tangential components of airgap flux density: (a) outer airgap; (b) inner airgap.

Figure 3. Motor output performance: (a) phase and line back-emf waveforms; (b) output torque waveform.

5. Conclusions

An analytical subdomain model has been presented for predicting the magnetic field distributions during open circuit and on-load conditions for DS-PMSM. The analytical results exhibit excellent agreement in comparison with FEA results. The high accuracy of the proposed analytical subdomain model can enable analysis of the performance of DS-PMSM within a much shorter computational duration repetitively and interactively.