Error Minimization in ECG Signal Reconstruction Using Discrete Wavelet Transform ^†

Abstract

For clinical study and diagnosis, compression of Electro Cardio Gram (ECG) signal is a fundamental step for processing. However, the compression and reconstruction introduce errors in the signal. Therefore, error minimization is crucial before using these signals for analysis and diagnosis. This paper presents an efficient method to minimize the reconstruction error using the adaptive filtering technique. Better reconstruction was achieved based on higher value of Compression Ratio and lesser value of Percent Root mean squared difference. Daubechies Wavelet easily detects the signal spikes while keeping less error rate using Least Mean Squared Error algorithm. However, the percentage value of error appeared to be minimum when using Daubechies Wavelet because of its small coefficients other than Haar and Coiflet Wavelet. Therefore, it was concluded that Daubechies Wavelet should have been used for error minimization in the reconstructed signal.

1. Introduction

Higher resolution Electro Cardio Gram (ECG) signals are composed over lengthy periods. The information generated for transmission is due to the substantial volume. The quantity of data is decreased by data compression that is essential for storage and transmission of digitized ECG signals without any loss in the quality of the signal. As storage space is comparatively cheap, the compression of ECG signal has attracted substantial concentration for many years. Numerous compression algorithms for ECG are based on the reduction of compression ratios. A brief description of ECG signal compression is presented along with transformation and optimization procedures [1].

The purpose of Wavelet Transform is to break down the selected signal into a number of signals called cluster of signals belonging to different frequency bands. For a short duration of wavelet, a center frequency is defined by wavelet analysis [2]. Different types of wavelet families will have different characteristics, these include Haar, Mexian hat, Morlet, Complex Morlet, Symmlet, Daubechies, Coiflets, Biorthogonal, and Meyer Wavelets. Wavelet families can further be subdivided into their orthogonal and bi-orthogonal wavelets based on their scaling and wavelet function [3]. The mathematical expression of a wavelet can be described using Equation (1) [4]. Wavelet (MW) is used for analysis [5]. ((t − τ)/s) is the ratio between shift in time and change in scale (big S means long wavelength).

$${\psi }_{s,\tau }(t)=\frac{1}{\sqrt{s}}\psi (\frac{t-\tau }{s})$$

(1)

where, ${\psi }_{s,\tau }$(t) is wavelet with scales’ and time $’\tau ’$(‘s’ and ‘${\tau }^{\prime }$ are integers for dilating and scaling function.). $\frac{1}{\sqrt{s}}$ is Normalization (Normalization by $\frac{1}{\sqrt{a}}$ ensures that $\left|\right|{\psi }_{a,b}\left(x\right)\left|\right|$ = $\left|\right|\psi \left(x\right)\left|\right|$ is independent of ‘a’ and ‘b’). Lastly, $\psi$ is parent wavelet.

The Direct Compression technique of Bio-electrical data reduces useless repetitions in data arrangement by exploring a sequential amount of adjacent signals. The signals compressed through the direct compression technique reduce the re-establishment fault in a number of signal samples that are to be taken [6]. The Direct Data Compression technique includes AZTEC, CORTES, Fan, SAPA, TP algorithm, Improved Modified AZTEC, and Delta coding [7]. Secondly, Transform Domain Compression Technique is preferable for the application of linear orthogonal transformation of ECG signals [8]. The original signal sample of ECG is subject to a transformation and the compression technique is performed in new domains like Fourier Transform (FT), Discrete Cosine Transform (DCT), wavelet, and JPEG 2000. These techniques create higher Compression Ratio than direct techniques [9]. Lastly, in parameter extraction methods of data compression, irreversible processes are used to maintain the parameters of the ECG signals [10]. This technique includes the dominant feature of extraction from samples of raw ECG signals using peak, picking up approach, and long-term prediction approach [11].

2. Methodology

The work methodology can be decomposed into the following steps:

• Taking the targeted ECG signal
• Quantization of ECG signal
• Selection of wavelet families for quantized signal
• Applying the mathematical equations of its wavelet and scaling coefficient for channel estimation
• For the removal of noise, using high pass and low filters, applying the adaptive filtering technique (RLS/LMS) for its noise removal
• Reconstruction of signal using IDWT
• De-quantization of ECG signal
• Error Minimization using CR and PRD parameters.

MIT-BIH database has been used to get input ECG signals. These signals are then compressed to be used for reconstruction using the proposed method explained below. Figure 1 details the proposed methodology in which the compression of Bio-electrical signal was achieved using DWT technique, it is used for the compression and filtering of Bio-electrical signal because it represents both the time and frequency domain of signal in multi-resolution mode. The signal is quantized, and a wavelet family was selected for channel estimation.

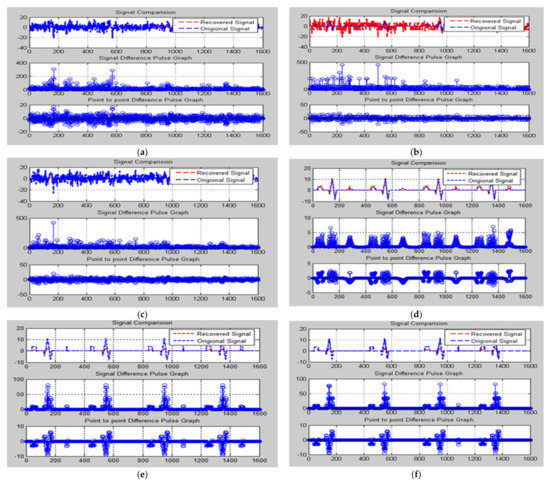
Figure 1. Adaptive filtering results using RLS and LMS, respectively. Each figure contains three outputs from top to bottom: Point to point difference pulse graph, signal difference pulse graph, and the reconstructed signal, respectively. (a) Result of Haar Wavelet by applying the adaptive filtering technique (RLS) (b) Result of Daubechies Wavelet by applying the adaptive filtering technique (RLS) (c) Result of Coiflet Wavelet by applying the adaptive filtering technique (RLS) (d) Result of Haar Wavelet by applying the adaptive filtering technique (LMS) (e) Result of Daubechies Wavelet by applying the adaptive filtering technique (LMS) (f) Result of Coiflet Wavelet by applying the adaptive filtering technique (LMS).

3. Results

The main purpose of an adaptive filter is to change (adapt) the coefficients of a FIR filter to match the response of an unknown system as closely as possible. The unknown system and the adapting filter process the same input signal and have the outputs. Adaptive filters are self-designing filters based on an algorithm that allows the filter to “learn” the initial input statistics and to track them if they are time-varying. These filters estimate the deterministic signal and remove the noise uncorrelated with the deterministic signal. Here, LMS and RLS have been used for noise reduction in adaptive filtration of signals.

The simulation model of Haar, Daubechies, Coiflet families and their results are provided in this section. We have considered two different cases as follows:

• Quantized/Compressed ECG Signal then apply adaptive filtering technique on it for which we use RLS (Recursive Least Square) algorithm.
• Quantized/Compressed ECG Signal then apply adaptive filtering technique on it for which we use LMS (Least Mean square Error) algorithm.

The selected wavelet families are Haar, Daubechies, and Coiflet. As shown in Figure 1, the reconstructed signal using Haar Wavelet with RLS and the maximum overlap with the original signal reflect minimum error rate as depicted in Figure 1a–c.

However, in Figure 1a, the Haar Wavelet with RLS has not shown good overlap. Furthermore, Daubechies and Coiflet have produced better results using RLS as compared to Harr Wavelet. Nevertheless, Daubechies Wavelets responses are significantly better than other techniques, as shown in Table 1 as well. Similarly, Figure 1d–f shows the wavelet results using LMS algorithm. The reconstructed signal showed better overlap as compared to RLS and therefore, it is preferred over RLS. Furthermore, Figure 1e shows minimum % error, where Daubechies wavelet has been used with LMS algorithm.

Table 1. Quantization of signal with adaptive filters by using RLS Algorithm.

Wavelet	CR	PRD	MSE	% Age Error
Haar	50	1.9239	2.2812	22%
Daubechies	50	0.8015	1.8304	3.7%
Coiflet	50	0.8056	1.8657	3.9%

Algorithm of adaptive filtration gives a minimum value of SNR and maximum value of PRD. Due to the opposite behavior of SNR and PRD reconstruction of the signal is not improved. Whereas, Adaptive filtering with LMS algorithm gives a maximum value of SNR and minimum value of PRD by using the proposed algorithm which is evident from Table 2.

Table 2. Quantization of signal with adaptive filters by using LMS Algorithm.

Wavelet	CR	PRD	MSE	% Age Error
Haar	50	0.3784	8.82	3%
Daubechies	50	0.8116	4.9599	2.8%
Coiflet	50	0.8128	4.2885	2.9%

4. Conclusions

In this research paper, the simulation results of Haar, Daubechies, and Coiflet are evaluated on the basis of parameters and percentage error. The results have shown that RLS algorithm of adaptive filtration by using Daubechies Wavelet family gives a better value of reconstruction that provides a minimum value of PRD (0.8015).