Wrist Photoplethysmography Pulse Waves: Morphological Classes and Physiological Influences ^†

Abstract

Wearables such as smartwatches provide opportunity for large-scale cardiovascular health monitoring. Wearables often use photoplethysmography (PPG), an optical sensing technique, to measure the arterial pulse wave and derive insights into cardiovascular physiology. Whilst there has been much research into the shape and physiological determinants of the finger-PPG pulse wave, much less is known about the wrist-PPG pulse wave. The aim of this study was to describe the morphology of wrist-PPG pulse waves and compare them with finger-PPG pulse waves. We analyzed wrist-PPG recordings from 686 adults in the Aurora-BP dataset. Visual inspection of pulse wave shapes revealed five classes of PPG pulse waves, three of which were similar to those seen in finger-PPG pulse waves, and two of which were different. An algorithm was developed to automatically classify wrist-PPG pulse waves and revealed variability in pulse wave shape within and between subjects. A multivariable regression analysis of associations between subject metadata and two features of pulse wave shape indicated that wrist-PPG pulse wave shape is associated with heart rate, body size (body size index and height), and blood pressure. No significant associations with age were observed, in contrast to previous findings on finger-PPG pulse waves. The differences observed between wrist- and finger-PPG pulse wave shapes indicate a need for greater understanding of the physiological origins of the wrist-PPG pulse wave and for the adaptation of algorithms specifically for wrist-PPG analysis.

1. Introduction

Cardiovascular disease (CVD) is the leading cause of mortality worldwide. Wearables may provide opportunity to monitor cardiovascular health in daily life and could be used to prompt lifestyle changes and to detect early signs of disease. Wearables such as smartwatches and smart rings often use photoplethysmography (PPG) for cardiovascular monitoring. PPG is a low-cost, non-invasive, optical sensing technique, which measures the arterial pulse wave—the variations in blood volume which occur each heartbeat as the pressure wave from the heart reaches the measurement site. The shape of the PPG pulse wave is influenced by both the heart and the blood vessels, making it a rich source of information on cardiovascular physiology [1]. Indeed, a growing body of work shows that the shape of the PPG pulse wave contains information on various aspects of cardiovascular physiology, including autonomic tone, blood pressure, and arterial stiffness [2]. Consequently, PW analysis is being explored for cuff-less blood-pressure estimation [3,4], vascular aging assessment [5], and evaluation of CVD risk [6]. Comprehensive overviews can be found in [7,8].

Since PPG has been used in finger pulse oximeters for several decades, much research in the PPG pulse wave has focused on finger-PPG pulse waves. In contrast, there has been much less research into the shape of wrist-PPG pulse waves. Given the widespread use of smartwatches, understanding wrist-PPG pulse wave shapes could inform large-scale cardiovascular monitoring.

This study aims to describe the morphology of wrist-PPG pulse waves and compare them with finger pulse waves. The objectives were (i) to identify classes of wrist-PPG pulse wave shapes and to compare these classes with those previously described for finger-PPG; (ii) to develop an automated algorithm to classify wrist-PPG pulse waves according to their shape; and (iii) to assess the physiological determinants of wrist-PPG morphology and compare them with those influencing finger-PPG.

2. Materials and Methods

Briefly, this study used wrist-PPG recordings from the Aurora-BP dataset [9] and wrist- and finger-PPG recordings from the MAUS dataset [10]. Preprocessed wrist- and finger-PPG recordings from the MAUS dataset were used to compare the shape of simultaneous wrist and finger pulse waves. Classes of wrist-PPG pulse wave shapes were identified by visually inspecting preprocessed pulse waves from the Aurora-BP dataset. An automated algorithm was developed to classify wrist-PPG pulse waves using a decision tree approach based on differences in pulse wave shapes between classes. Physiological determinants were assessed by using linear regression to investigate associations between pulse wave shape features (rise-time and AUC) and physiological factors.

Only fully anonymized data were used. No additional ethical approval was acquired. The code used is available at https://github.com/ad045/wrist-ppg-morphology (accessed on 11 August 2025).

2.1. Datasets

Two datasets were used in this study. The primary dataset was the Aurora-BP dataset [9], which includes wrist-PPG recordings collected from adults in laboratory conditions. We extracted the initial-visit, supine recordings from the participants performing either the oscillometric or auscultatory protocol (with our sample lasting on average ~25 s; both protocols utilized PPG sampling rates of 500 Hz), and available participant metadata. We chose to use the supine recordings, as these have previously been found to be of higher quality than sitting or standing recordings [11]. We only included recordings that met stringent quality criteria (optical quality > 0.80; tonometric quality > 0.65 on 0–1 scales; PPG recording longer than 15 s). We excluded participants with major cardiovascular comorbidities other than high blood pressure (namely, coronary artery disease, diabetes, arrhythmia, prior myocardial infarction or stroke, heart failure, aortic stenosis, valvular disease, or other CVD). The dataset was used to identify different prototypical morphologies of wrist pulse waves and to investigate physiological influences of pulse wave morphology.

The second dataset was the MAUS dataset [10], which includes simultaneous wrist- and finger-PPG recordings collected from graduate students in laboratory conditions. We extracted the seated resting segment collected before a cognitive-load task (lasting ~5 min, wrist-PPG at 100 Hz and finger-PPG at 250 Hz). Data from all participants were included in the analysis. The dataset was used to investigate differences between wrist and finger morphologies qualitatively and to compare the results of preprocessing pipelines at the wrist and finger. The MAUS dataset does not contain detailed participant metadata and therefore was not used for quantitative analyses.

2.2. PPG Signal Preprocessing

Aurora-BP wrist-PPG recordings were preprocessed using the pyPPG Python library [12], version 1.0.0, as follows. Signals were band-pass-filtered between 0.5 and 12 Hz. Then, individual pulse waves were extracted utilizing ‘find_peaks’ (from the Python library scipy, version 1.15.3) on the inverted signal with an initially set beat period of 1.0 s, minimum spacing of 0.5 s, and prominence ≥ 0.02 (relative units). Only pulse waves with a duration between 0.4 and 1.6 s were included in the analysis (±60 % around the initially set 1.0 s period, corresponding to heart rates between 38 and 150 bpm). Each pulse wave was linearly resampled to be 1000 samples in length (0–100 % cycle), detrended (first-to-last baseline removed), and amplitude-normalized to occupy a range of [−1, +1]. Also, any pulse wave whose mid-segment (samples 300–600 after resampling) contained a sample of <−0.1 was excluded from the analysis, thus excluding clipped or motion-distorted pulses.

The derivatives of each pulse wave were calculated as follows: Each pulse wave was repeated 20 times to generate a signal containing 20 repeated pulse waves. Then, the first three derivatives were calculated using pyPPG, and an additional fourth derivative was calculated. The central (11th) pulse wave was extracted to obtain smooth derivatives free of edge artifacts. The derivatives are denoted as VPG, APG, and JPG.

Finally, for every individual, pulse waves were ensemble-averaged by taking the mean of all clean pulse waves (and their derivatives), producing one representative pulse wave (and one representative wave for each derivative) per subject.

2.3. PPG Pulse Wave Feature Extraction

Two features were extracted from each pulse wave: the previously proposed rise-time parameter [13], and a novel parameter denoted AUC (positive area under the mid-part of the APG curve). The rise-time was computed as the time from pulse wave onset to maximum peak for each individual pulse wave; the median of this was calculated per individual. The AUC was proposed as a novel parameter to capture observed differences in wrist-PPG pulse wave morphology between classes. It was calculated as the area under the ensemble second derivative (APG) above zero between 20% and 80% of the wave duration, multiplied by −1 if the wave was classified as Class I or Class II.

2.4. Defining Classes of Wrist-PPG Pulse Wave Shapes

Classes of wrist-PPG pulse wave shapes were identified and defined as follows. First, the preprocessed wrist-PPG pulse waves from the Aurora-BP dataset were visually inspected to identify categories of pulse wave shape (aiming to cover all the general pulse wave shapes observed in the data). Second, any categories which were similar to each other were combined to produce the final classes of pulse wave shape. The approach of defining discrete morphological classes of pulse wave shape is in line with previous work by Dawber et al. [14] and Zanelli et al. [15]. Pulse wave classes were illustrated visually with representative examples and described mathematically. The newly proposed wrist-PPG classes were compared with those previously proposed for the finger-PPG.

2.5. Developing an Automated Algorithm to Classify Wrist-PPG Pulse Waves

An automated algorithm was developed to classify wrist-PPG pulse waves as follows. First, the morphology of each pulse wave class was described in terms of the number of peaks in the pulse wave, their relative amplitudes, and (in the case of pulse waves with only one peak) the position of the inflection point in relation to the peak. Second, a decision tree algorithm was designed to classify pulse waves according to these characteristics. Third, the algorithm was extended to quantify the ‘sharpness’ of the notch between the first and second peaks using the AUC parameter. This enabled a continuous measure of pulse wave shape, in addition to the categorical measure provided by the pulse wave classes.

2.6. Assessing the Physiological Determinants of Wrist-PPG Morphology

The physiological determinants of wrist-PPG morphology were assessed by investigating the associations between participant metadata and pulse wave features. The following metadata variables were included: heart rate (HR), body mass index (BMI), age, height, and systolic and diastolic blood pressure (SBP and DBP). The two pulse wave features were rise-time and AUC (as described in Section 2.3). Associations were investigated using multiple linear regression. To do so, continuous predictors were z-scored, and then multiple linear regression (ordinary least squares performed with the statsmodels library in Python, version 0.14.4) was performed to investigate determinants of each of the pulse wave features.

3. Results

3.1. Dataset Characteristics

Wrist-PPG recordings from a total of 686 subjects (340 female and 346 male) in the Aurora-BP dataset met the inclusion criteria and were therefore included in the analysis. Summary characteristics can be found in

Table 1. Dataset characteristics. Values are provided as mean ± standard deviation, if not stated otherwise. Only limited metadata were available for the MAUS dataset.

Characteristic	Aurora-BP	MAUS
Recording site	Wrist	Finger and wrist
Number of subjects	686	22
Gender [percentage female]	49.56 %	9.09 %
Age [years]	43.98 ± 11.26	23 ± 1.7
Height [m]	1.72 ± 0.1	-
BMI [kg/m2]	28.54 ± 6.23	-
SBP [mmHg]	124.72 ± 16.72	-
DBP [mmHg]	76.14 ± 11.18	-
Heart rate [bpm]	65.83 ± 9.8	-
Recording duration [s]	24.64 ± 5.59	Finger: 299.41 ± 1.84 Wrist: 299.92 ± 2.23

. The mean (±SD) rise-time across subjects was 0.34 ± 0.09 s. A total of 17,873 individual wrist pulse waves were included in the analysis.

3.2. Comparing Finger- and Wrist-PPG Pulse Waves

Simultaneous finger- and wrist-PPG recordings from the MAUS dataset showed clear differences in pulse wave morphology between the two sites (see Figure 1). After amplitude and duration normalization, finger pulses showed an earlier, steeper systolic upstroke and sharper peak, with more distinct secondary (dicrotic) features. Wrist pulses appeared broader, with a later peak and a more symmetric contour.

3.3. Identifying Classes of Wrist-PPG Pulse Wave Shapes

The process for identifying classes of wrist-PPG pulse wave shapes consisted of (i) identifying categories of pulse wave shape and (ii) combining some of these categories to produce a final set of pulse wave classes.

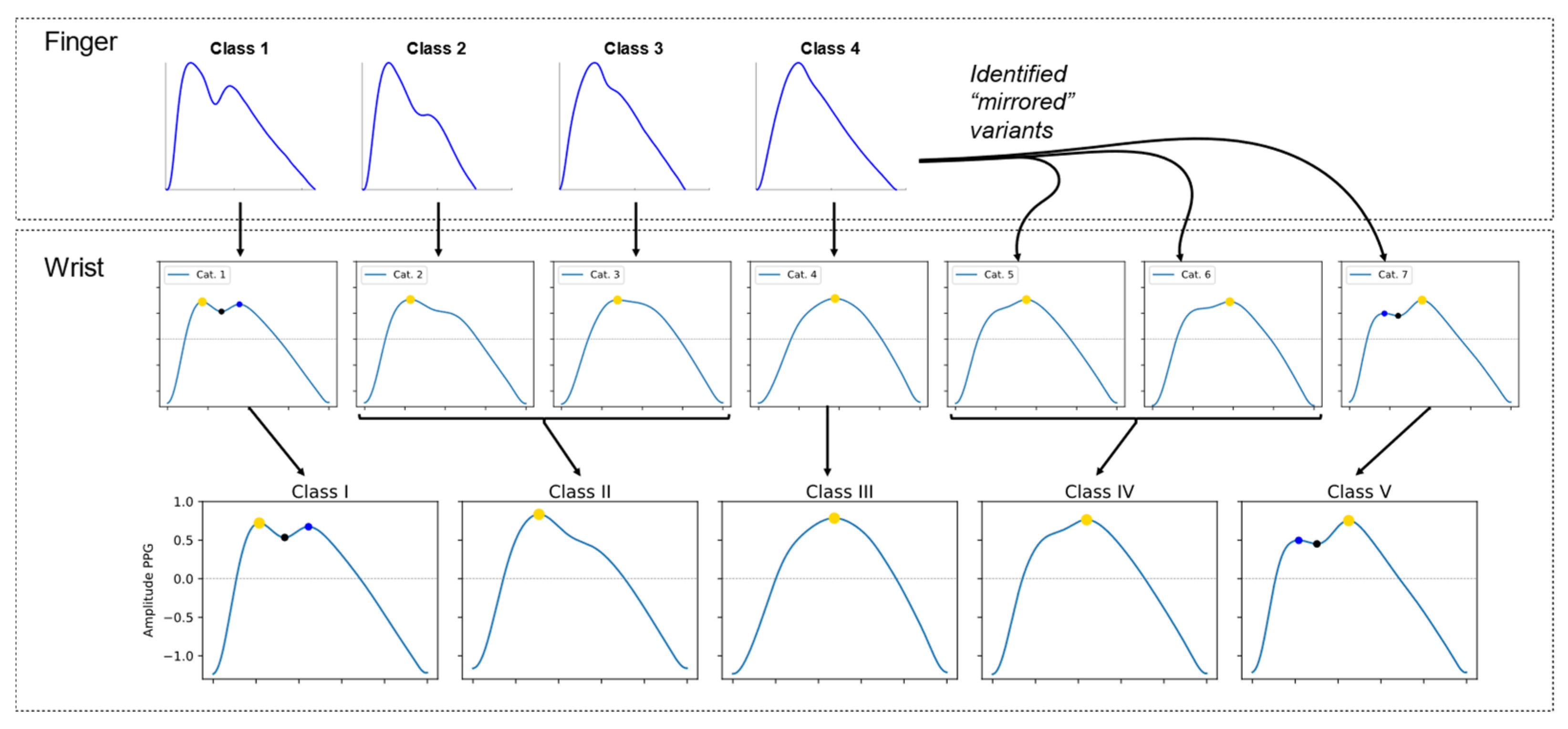
We identified seven categories of wrist-PPG pulse wave shape, as illustrated in Figure 2 (middle row). The first four categories (cat. 1–4) of wrist-PPG pulse wave shape corresponded closely with the four previously proposed classes of finger-PPG pulse wave shape, as shown in Figure 2 (top row) [5]. These first four categories each consisted of a dominant systolic peak. followed by one of the following: (cat. 1) a smaller dicrotic-like peak, (cat. 2) a shelf-shaped inflection, (cat. 3) a subtle change in downslope angle, or (cat. 4) no discernible secondary feature. In addition, we observed three additional categories of wrist-PPG pulse wave shape (cat. 5–7) which did not correspond to any of the four previously proposed finger-PPG classes. Instead, these additional wrist-PPG categories (cat. 5–7) appeared to be mirror versions of finger-PPG classes (1–3).

We defined five classes of wrist-PPG pulse wave shape by combining some of the observed categories. Specifically, categories 2 and 3 were combined into a single class, and categories 5 and 6 were also combined into a single class, as illustrated in the middle and lower rows of Figure 2. These were combined because there was minimal difference between the appearance of a shelf-shaped inflection (categories 2 and 5), and a subtle change in downslope angle (categories 3 and 6).

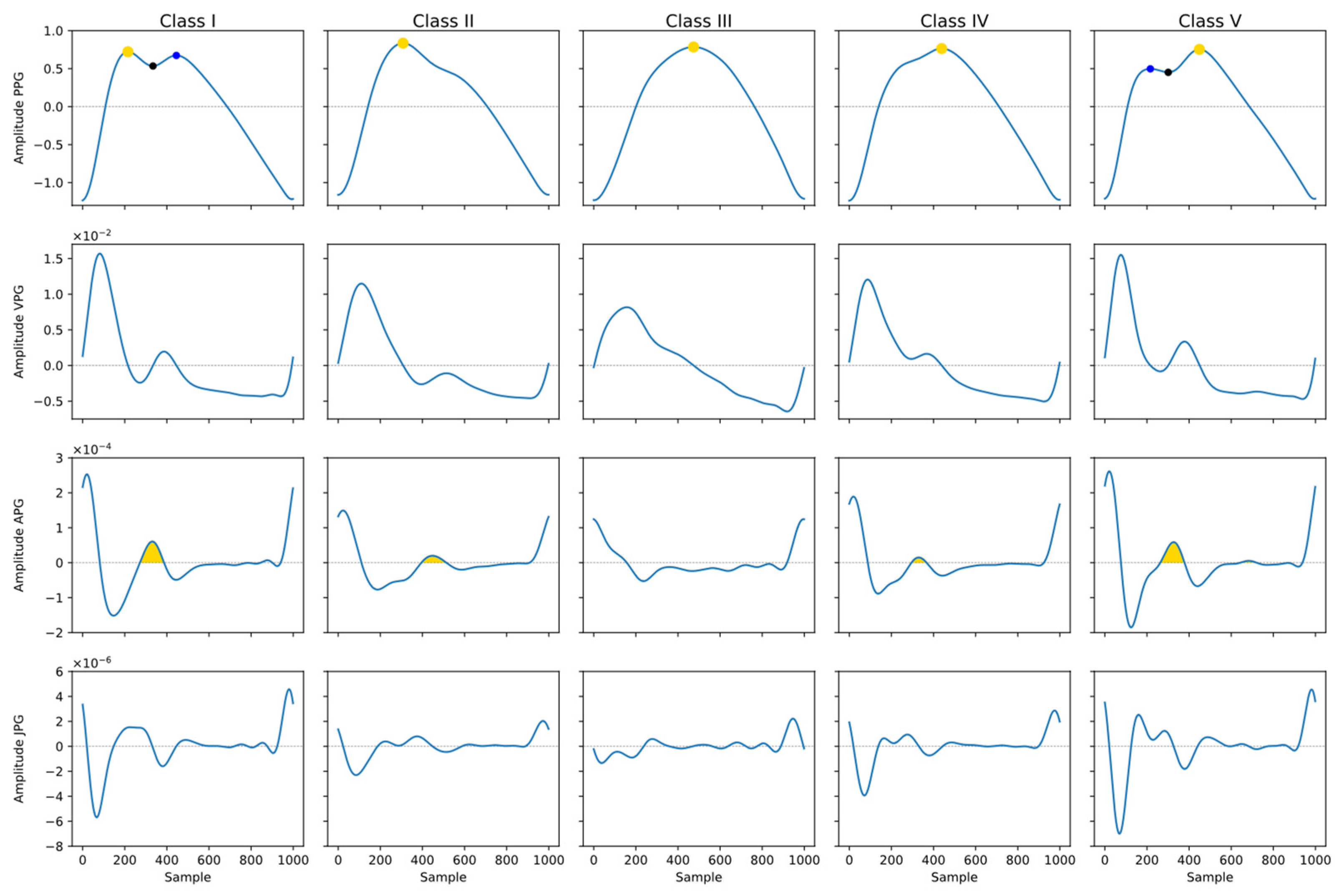
The five defined classes of wrist-PPG pulse wave shape are illustrated in Figure 3 (top row) alongside their derivatives (remaining rows). The classes are denoted Class I–Class V. Class I shows two peaks, with the first peak being of higher amplitude than the second. Class II shows one peak, followed by a change in angle (inflection point) on the downslope. Class III shows one peak with no discernible change in angle (inflection point). Class IV shows one peak, preceded by a change in angle (inflection point) on the upslope. Class V shows two peaks, with the second peak being of higher amplitude than the first. The five wrist-PPG classes and their comparison with finger-PPG classes are summarized in

Table 2. Morphological descriptions of the five wrist-PPG pulse wave classes, and their prevalence in the individual pulse waves that were identified in the AURORA-BP dataset.

Class	Equivalent Finger Class	Morphology	Percentage in Sample
I	1	Two peaks, first peak > second peak	6.5
II	2/3	One peak + change in angle/inflection on downslope	41.2
III	4	Single peak, no evidence of second component	24.1
IV	-	One peak + change in angle/inflection on upslope	23.2
V	-	Two peaks, first peak < second peak	5.0

.

3.4. An Automated Algorithm to Classify Wrist-PPG Pulse Waves

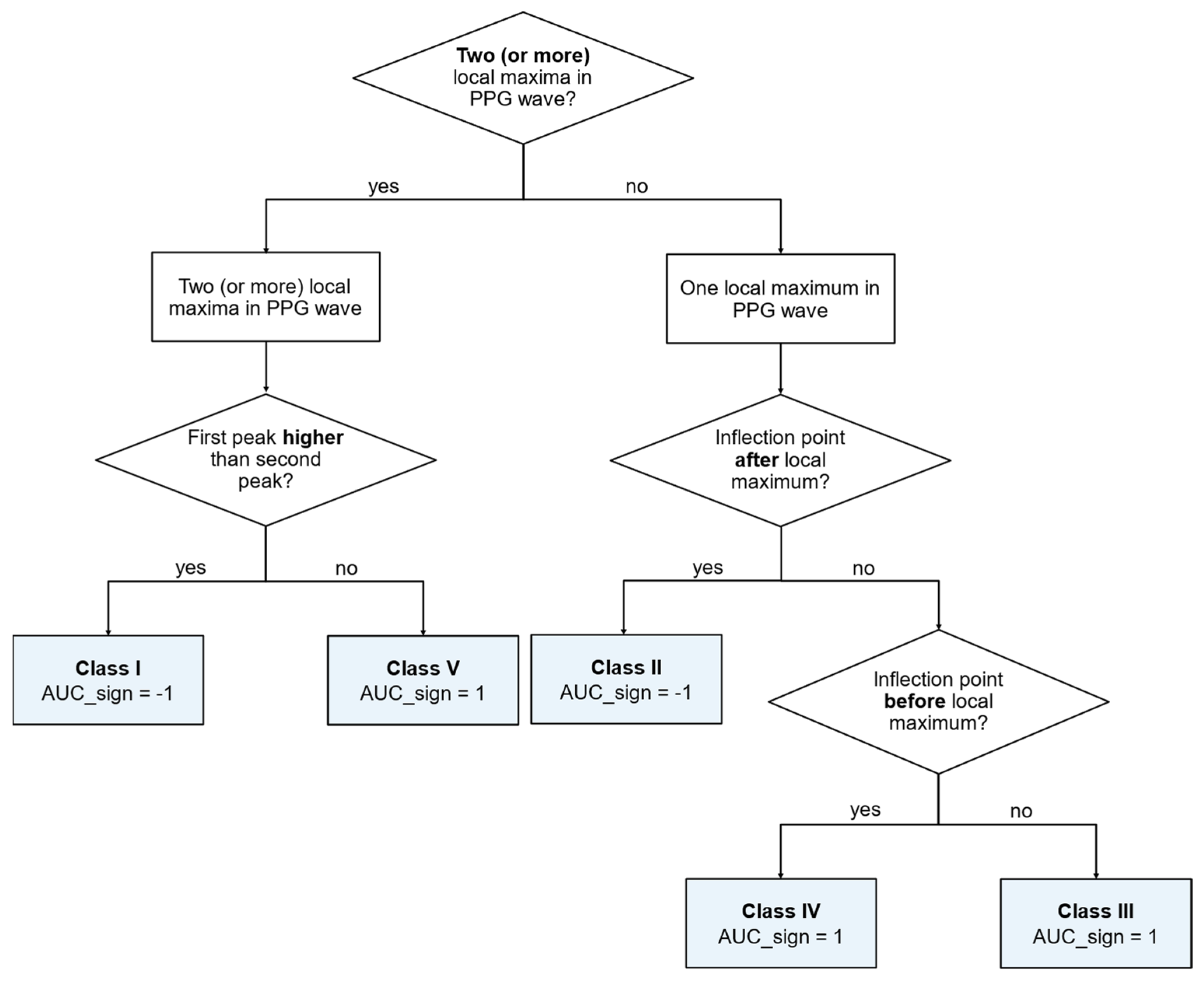
An automated algorithm to classify wrist-PPG pulse waves was developed based on the differences in morphologies between the five classes. The morphologies of the five classes are described in Table 2. The algorithm presented in Figure 4 was used for classification; classification was performed by decision rules based on (i) the number of peaks in the pulse wave; (ii) their relative amplitudes; and (iii) in the case of pulse waves with only one peak, the position of the inflection point in relation to the peak.

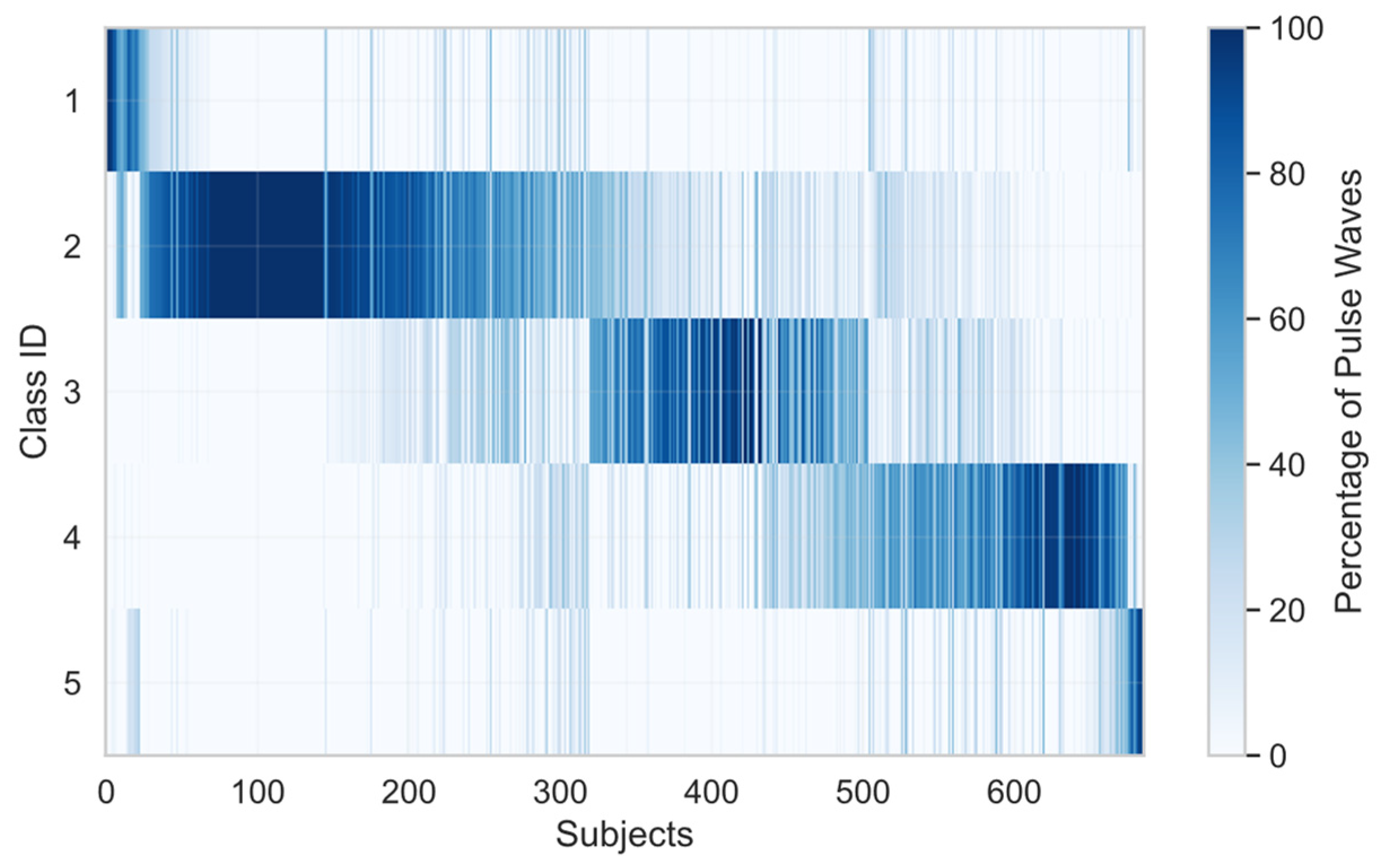
The algorithm was used to classify the individual pulse wave of each Aurora-BP participant. The distribution of pulse wave classes is summarized in Table 2. Figure 5 illustrates the distribution of pulse wave classes. It demonstrates that as well as variation between subjects, there was also variation within individual subjects; i.e., most recordings contained a mixture of pulse wave classes. This demonstrates that a single canonical waveform per subject is the exception rather than the rule.

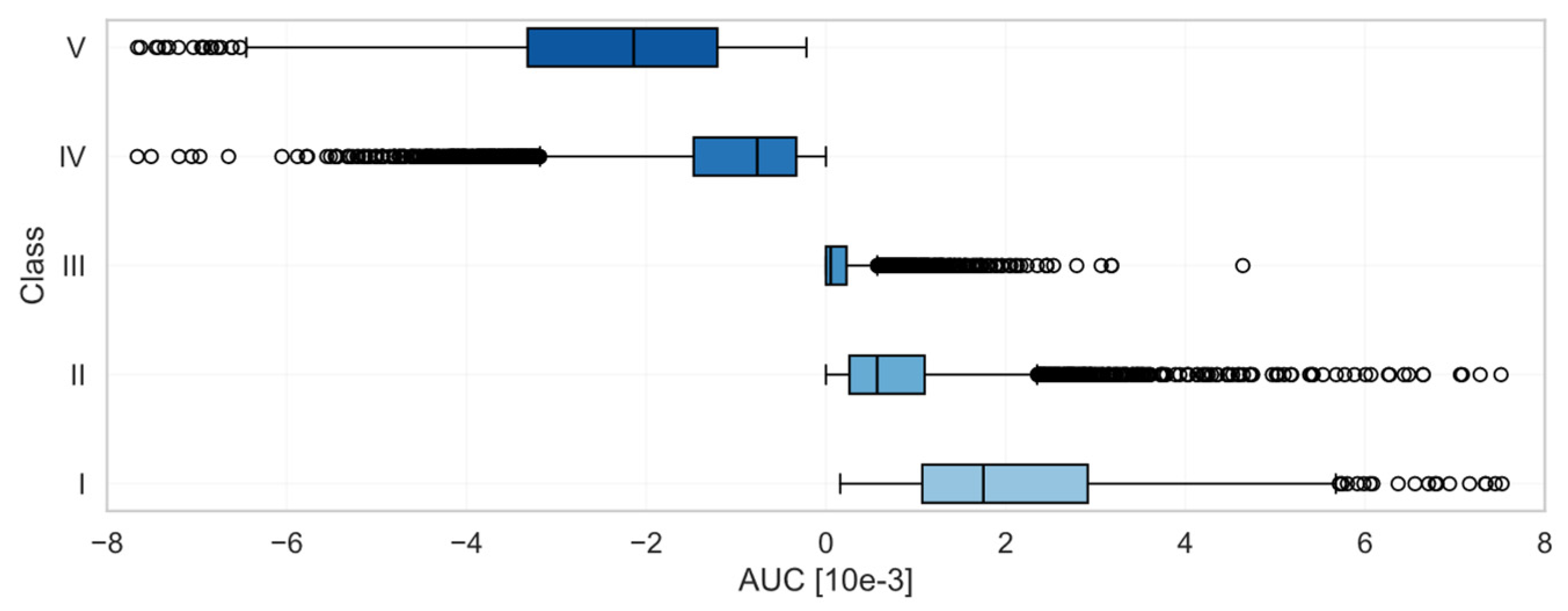
The algorithm was then extended by calculating the AUC to provide a continuous measure of pulse wave shape. Figure 6 shows the distribution of AUCs for each pulse wave class. The AUC generally increased from its lowest negative values for Class I pulse waves, to values close to 0 for Class III pulse waves, and its highest positive values in Class V. The AUC therefore corresponded well with the classes, but provided a continuous measure of pulse wave shape as opposed to the discrete measure provided by the classes. In summary, Figure 5 demonstrates inter- and intra-subject variability in pulse wave classes, while Figure 6 confirms that the discrete classification aligns with the continuous AUC descriptor.

3.5. Physiological Determinants of Wrist-PPG Morphology

The results of the regression analyses used to identify determinants of wrist-PPG morphology are shown in

Table 3. Multivariate analysis (OLS), 686 datapoints. All variables were z-normalized. For rise-time, R² = 0.540; adjusted R² = 0.536; F-statistic = 132.8; prob (F-statistic) = 5.88 × 10⁻¹¹¹. For AUC, R² = 0.195; adjusted R² = 0.188; F-statistic = 27.45; prob (F-statistic) = 2.17 × 10⁻²⁹. Bold numbers indicate statistical significance at p < 0.05.

	Rise-Time [ms]			AUC
Variable	β	Std Err	p > |t|	β	Std Err	p > |t|
Const	0.3435	0.002	0.000	−0.0002	2.88 × 10−5	0.000
Age	−0.0041	0.002	0.094	3.946 × 10−5	3.04 × 10−5	0.195
BMI	−0.0184	0.002	0.000	−0.0002	3.01 × 10−5	0.000
Height	−0.0091	0.002	0.000	−0.0001	3.00 × 10−5	0.000
HR	−0.0607	0.002	0.000	−0.0003	2.99 × 10−5	0.000
SBP	−0.0079	0.004	0.034	−5.91 × 10−5	4.61 × 10−5	0.200
DBP	0.0161	0.004	0.000	0.0002	4.43 × 10−5	0.000

. Together, the metadata variables explained approximately half of the variance in rise-time (adj. R² = 0.536), whereas they only explained approximately 19% of the variance in AUC (adj. R² = 0.188). For rise-time, heart rate was identified as the dominant determinant (β = −0.0607; p < 0.001): every 1 SD increase in HR was associated with a reduction in rise-time of ~0.06 SD. Increased BMI and height were also associated with decreased rise-time (β ≈ −0.0184 and −0.0091; both p < 0.001), while increased DBP was associated with increased rise-time (β ≈ 0.0161; p < 0.001). SBP had a weaker negative association (p < 0.05), while age was not significantly associated with rise-time in this multivariate analysis. AUC was associated with similar determinants: heart rate, BMI, height, and DBP; once again, heart rate was the dominant determinant and there was no significant association with age. 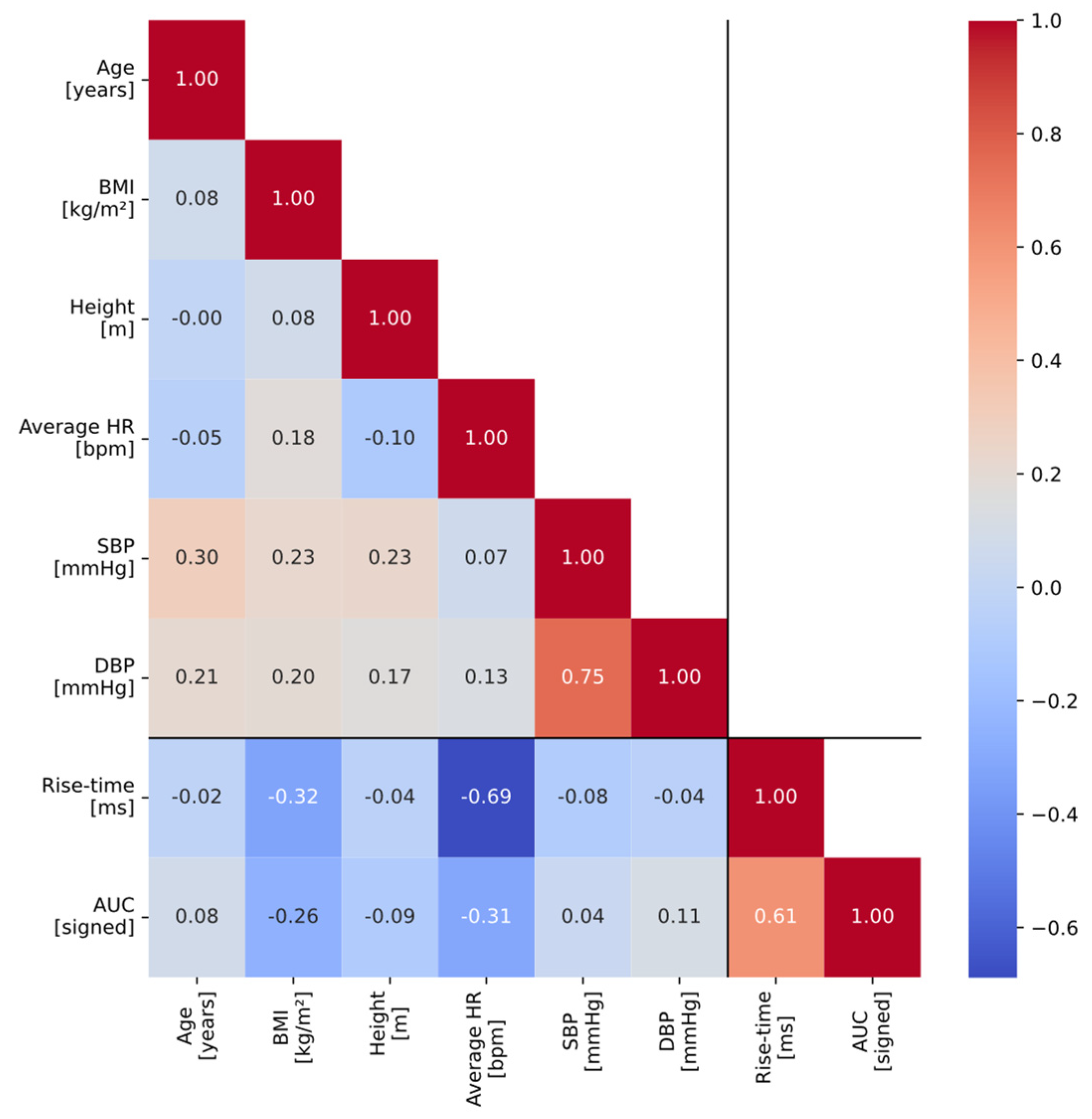The correlation coefficients (Pearson’s r values) between different variables (metadata and pulse wave features) can be found in Figure 7.

4. Discussion

4.1. Summary of Findings

We identified five classes of wrist-PPG pulse wave shape, defined as follows: Class I—a higher peak followed by a lower second peak; Class II—a peak followed by an inflection point on the downslope; Class III—a peak with no evidence of a second component; Class IV—an inflection point on the upslope followed by a peak; and Class V—a lower peak followed by a higher second peak. These five classes include the morphologies commonly encountered in finger-PPG pulse waves (Classes I–III), and additional morphologies not often seen in finger-PPG pulse waves (Classes IV and V). These clear differences between the morphology of finger- and wrist-PPG pulse waves were also observed when comparing simultaneous finger and wrist recordings.

A simple algorithm was designed to classify wrist-PPG pulse waves into the five classes of pulse wave shape. This algorithm is a decision tree containing decision rules about the number of peaks, their relative amplitudes, and (in the case of pulse waves with only a single peak) the position of any inflection point relative to the peak. In addition, a novel feature denoted AUC was designed to quantify the prominence of the notch in wrist-PPG pulse waves, providing a continuous measure of this particular aspect of pulse wave shape.

When using this algorithm to analyze continuous recordings, we found that individual subjects did not exhibit just one class of pulse wave shape, but often their pulse waves spanned multiple classes. When quantifying pulse wave shape using two features (rise-time and AUC), we found that the variability in pulse wave shape was only partially explained by subject characteristics (principally heart rate, BMI, and diastolic blood pressure). Notably, there were no significant associations with age.

4.2. Comparison with the Existing Literature

Previous studies have identified classes of different types of pulse waves. Dawber et al. proposed four classes of finger pressure pulse waves [14], with shapes similar to categories 1–4 in Figure 2. These four classes were defined according to their dicrotic notch characteristics. Charlton et al. applied Dawber’s classes to finger-PPG pulse waves [5]. Zanelli et al. used unsupervised clustering algorithms to identify seven clusters of finger-PPG pulse waves, which differed not only according to their dicrotic notch characteristics but also other characteristics such as the width of the systolic peak [15]. To our knowledge, the current study is the first to identify classes of wrist-PPG pulse waves. In this study we used visual inspection to identify classes, similarly to Dawber et al. In the future, unsupervised clustering algorithms such as those used by Zanelli et al. could be used to refine the identified classes, accounting for multiple pulse wave characteristics rather than focusing primarily on the dicrotic notch. In addition, Dawber et al. and Zanelli et al. assessed the clinical interpretation of their identified classes. Investigating the clinical interpretations of wrist-PPG pulse wave classes could help create potential use cases for them.

A key finding of the current study was that wrist-PPG pulse wave shape was determined primarily by heart rate, body size (BMI), and blood pressure (diastolic), but not by age. In a multivariate regression analysis on rise-time, similar to the current study, Allen et al. found that finger-PPG pulse wave shape was also associated with heart rate and body size (height in their case), but not blood pressure [13]. In addition, the strongest association identified by Allen et al. was with age, indicating a potential difference between finger- and wrist-PPG pulse waves: finger-PPG pulse wave shape is strongly determined by age, whereas wrist-PPG pulse wave shape did not appear to be so in the current study.

4.3. Strengths and Limitations

There are several strengths to this study. First, it was performed using a large dataset with a wide range of subject characteristics (age, BP, and BMI). Second, the analysis included only data from subjects without cardiovascular diseases (with the exception of hypertension), thereby avoiding the potential confounding effects of abnormal hemodynamics on pulse wave analysis. In addition, only high-quality data recorded under laboratory conditions were included to reduce any influence of noise on the results. Third, the study utilized a range of methodologies to investigate the morphology of wrist-PPG pulse waves, including visual inspection, visual comparison with finger-PPG pulse waves, automated analysis, and regression analyses to identify associations between subject characteristics and pulse wave shape. Fourth, ensemble-averaging was used to minimize the within-subject variance in regression analyses.

There are also limitations to the work. First, the data used in this work were collected using particular devices, such as the green-wavelength PPG acquisition in the Aurora-BP dataset, and therefore the results may not be generalizable to other devices and sensor designs. Second, the data were collected in the supine position, and potentially wrist-PPG pulse wave shape could vary between different postures. However, we anticipate that it is most important to understand wrist-PPG characteristics in the supine position, as detailed analyses of pulse wave shape are often performed whilst subjects are asleep. Third, the data were collected in a controlled laboratory setting with minimal motion artifact, and therefore it is likely that additional steps would be required to perform automated analyses of wearable data in free-living conditions. Fourth, whilst the visual comparison between wrist- and finger-PPG pulse wave shapes from the MAUS dataset was informative, we did not perform a quantitative comparison between the two sites. The MAUS dataset is small and only contains data from a narrow range of ages, and in the future it may be helpful to use larger datasets to compare pulse wave shapes between anatomical sites.

4.4. Implications and Future Work

This study indicates that wrist-PPG pulse waves differ from finger pulse waves, and the physiological determinants of wrist-PPG pulse waves may differ from the determinants of finger pulse waves. This has two key implementations. First, signal processing algorithms developed for finger-PPG pulse waves may not function correctly on wrist-PPG pulse waves. For instance, a finger-PPG algorithm may use the assumption that the highest point on the pulse wave corresponds to the first peak. However, this is not the case in Classes IV and V of wrist-PPG pulse waves. Therefore, such an algorithm may not correctly detect the additional points on a wrist-PPG pulse wave. Second, the potential use cases of wrist-PPG pulse waves may differ from those of finger-PPG pulse waves because of differences in their physiological determinants. For instance, previous work has found a strong association between age and rise-time extracted from finger-PPG pulse waves [13], whereas in this study we found no significant correlation between age and rise-time extracted from wrist-PPG pulse waves. Therefore, the wrist-PPG pulse wave may not be as useful as the finger-PPG pulse wave for assessing vascular aging. Conversely, the wrist-PPG pulse wave may be influenced by different physiological characteristics compared to the finger-PPG, such as microcirculatory properties, and therefore may be better suited to alternative use cases.

This study identified a strong association between wrist-PPG pulse wave features and heart rate, which may have implications for the analysis of wrist-PPG pulse waves. When using wrist-PPG pulse wave features to gain physiological insights, it may be helpful to normalize features by heart rate, thus reducing the impact of heart rate on them and enabling comparisons of features despite changes in heart rate. This approach is already used in ECG analysis, such as normalizing the QT-interval by RR-interval to produce the ‘corrected QT-interval’ parameter. As well as heart rate, we found BMI to be significantly associated with wrist-PPG pulse wave features, which may be helpful in some use cases and require normalization in other use cases.

Further research is needed to develop a detailed understanding of the physiological determinants of wrist-PPG pulse wave shape. Such an understanding would support the identification of suitable applications for wrist-PPG devices, such as which aspects of cardiovascular physiology can be assessed and which pathological states might be manifested.

5. Conclusions

In this study we identified five classes of wrist-PPG pulse wave shape. These included the morphologies commonly encountered in finger-PPG pulse waves, as well as additional morphologies not often seen in finger-PPG pulse waves. This highlights differences in the morphologies of finger- and wrist-PPG pulse waves. A simple algorithm was designed to classify wrist-PPG pulse waves into the five classes, and a novel feature of pulse wave shape was proposed to provide a continuous measure of pulse wave shape. Differences in wrist-PPG pulse wave shape were observed both within and between subjects. Wrist-PPG pulse wave shape was found to be associated with heart rate, BMI, and diastolic blood pressure, but unlike for the finger, there were no significant associations with age.

This study highlights the need to develop further understanding of the determinants of the wrist-PPG pulse wave shape to select suitable use cases for wrist-PPG devices. Furthermore, signal processing algorithms may need to be adapted for analysis of wrist-PPG pulse waves, rather than using those previously proposed for the finger-PPG.