Energy Harvesting for a Microscale Biosensing Device via Piezoelectric Micromachined Ultrasonic Transducers ^†

Abstract

Microdevices with dimensions comparable to a blood cell, i.e., tens of micrometers, show great potential for use in the human body. They can be adopted to identify the source of diseases, track their evolution and enhance the effectiveness of therapies, significantly improving patients’ quality of life. A key challenge is how to power the devices, which should ideally be performed wirelessly from a remote source. Piezoelectric micromachined ultrasonic transducers (pMUTs) offer a solution thanks to their ability to generate and collect energy via acoustic waves. In this work, numerical simulations of transmitter pMUT arrays are performed with the aim of generating an acoustic wave synchronized with a single pMUT or pMUT array receiver. The latter is intended for insertion in the human body. The characteristics required to switch on and power nano-electronics, in terms of generated voltage and electrical power at the receiver, are studied in ballistic gel, a material that mimics human organs. The focus is on a bio-compatible material for the piezoelectric layer, i.e., aluminum nitride enriched with scandium. Coupled electromechanical and acoustic simulations show that, of the considered pMUT devices, an 8 × 8 transmitter array combined with a single-device receiver (with a 50 µm pitch) or a 2 × 2 receiver array provide alternative options, with each offering advantages in terms of voltage amplitude or power at a steady state. The overall dimensions of the receiver, at a maximum of only 100 × 100 µm², is compatible with a future proof-of-concept biosensing platform test chip.

1. Introduction

Microscale biosensing devices have rapidly emerged as a fundamental medical tool for health monitoring, dramatically enhancing the effectiveness of therapies [1]. Recent advances in biomedicine and microelectronics, which have brought about the development of medical implants with dimensions at the tens-of-micrometers scale, require the identification of efficient, wireless and miniaturized energy sources that can substitute conventional batteries, which are bulky and have limited lifespans [2].

These miniaturized devices have ground-breaking applications in dry eye disease treatment [3], cancer tracking, diagnosis [4,5] and curing brain disorders [6], and the non-invasive, real-time monitoring [7,8] of metabolites, biomarkers, drugs and pathogens, aiming to identify the source and to track the evolution of disease [9]. First, ultrasound waves are a more safe and efficient transmission medium compared to electromagnetic waves, having higher safe exposure limits and shorter wavelengths that enable deeper penetration into the human body and, consequently, higher derivable power to the biosensing device. In addition, thin-film piezoelectric layers are able to efficiently convert acoustic energy into electrical energy despite their miniaturized size. This characteristic allows the design of microscale devices that work at frequencies in the megahertz range, providing high operational speed and optimal coupling with high-impedance fluids. Lastly, the choice of scandium aluminum nitride (ScAlN) as piezoelectric material, over the commonly used lead zirconate titanate (PZT), makes the device bio- and CMOS-compatible, ideal for the design of microscale biosensors. Piezoelectric micromachined ultrasonic transducers (pMUTs) [10,11] represent a promising solution for the energy harvesting of biomedical devices for multiple reasons [12,13].

In this paper, numerical simulations of one of the Sc_0.15Al_0.85N pMUTs reported in [14] are carried out to evaluate the operating frequency, derivable power and voltage of the selected devices, and to understand the energy-harvesting capabilities of receivers with very small areas, in the order of 100 × 100 µm². The analysis is conducted coupling the pMUT with ballistic gel, as reported in [15], which most closely mimics the acoustic properties of the relevant human tissue.

The remainder of the contribution is arranged as follows. Section 2 discusses the selected device, describing its geometrical parameters, piezoelectric properties and design frequency, together with details related to the numerical simulation. In Section 3, frequency domain analyses are presented to evaluate the performance of the transmitter (Tx) (8 × 8 array) and of the receiver (Rx), along with studies on cross-talk effects and acoustic coupling. Section 4 presents a time domain analysis of the whole setup, where Tx and Rx are placed 5 mm distant from each other in ballistic gel, to compute the collected voltage and the derivable power. The Section also discusses some fundamental aspects related to human tissue, such as acoustic attenuation of the material and safe exposure limits. In Section 5, final conclusions are drawn along with further developments of the current work. Used abbreviations are collected at the end of the paper.

2. Description of the pMUT Devices and Numerical Setup

In [14], six different Sc_0.15Al_0.85N pMUTs are presented: three devices are designed for air-coupled applications, while the other three are designed for water-coupled applications. With the ballistic gel being a high-impedance acoustic medium, comparable to water, the last three pMUTs are ideal for the required application. Among these devices, the smallest one, called R19 (labeled by its cavity radius), was chosen to comply with the Rx area constraints (100 × 100 µm²). 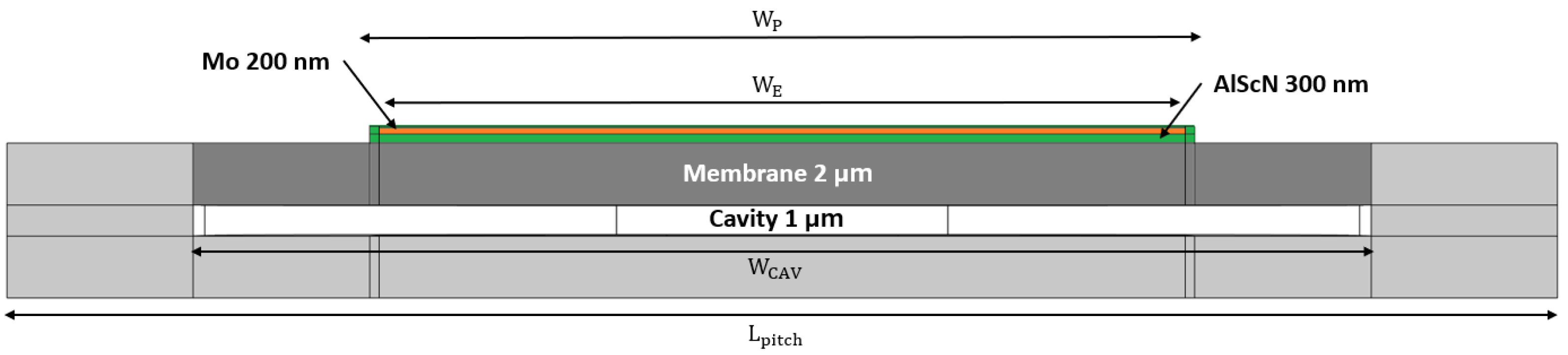The selected device features a square pitch with a side length of L_pitch = 50 μm, meaning that it is possible to employ a 2 × 2 array as the Rx, enhancing the collected energy and power, reducing the overall impedance of the device and enabling a larger transmit power in case the signal is sent back. The cross section of the R19 pMUT is depicted in Figure 1.

Its multi-layered structure is composed of a monocrystalline silicon (Si) substrate, etched to insert a cavity of 1 μm and a Si membrane of 2 μm. Selective areas of the Si layer are locally doped with phosphorous, setting the bottom surface of the piezoelectric layer to ground and avoiding the design of a metal bottom electrode. Then, a ScAlN layer of 300 nm and a molybdenum (Mo) layer, which acts as the top electrode, of 200 nm are deposited on the silicon membrane. To protect the Mo electrode from oxidation due to exposure to the external environment, an additional 50 nm coating layer of piezoelectric material is applied. Lastly, silicon dioxide (SiO₂) is deposited and etched to serve as insulation layer for aluminum (Al) tracks, which act as parallel interconnections for all pMUTs. SiO₂ and Al will not be considered for the numerical simulations, since they do not influence the pMUT dynamics.

With the exception of the Si pitch that has a square shape, the different layers are designed as sides of a square with rounded corners. The diameters of each layer are summarized in

Table 1. Geometrical parameters of the R19 device. The Si membrane has the same width as the cavity, while W_P is computed as 70 % of W_CAV.

Device	${\mathit{W}}_{\mathbf{CAV}}$ (µm)	${\mathit{W}}_{\mathit{E}}$ (µm)	${\mathit{W}}_{\mathbf{P}}$ (µm)
R19	38	26	26.6

.

The R19 pMUT has been modeled in COMSOL 6.3 Multiphysics^® to evaluate its design frequency and to check, through a transient analysis over time, the operating conditions from Tx to Rx in a ballistic gel medium. In the following subsections, the materials, the boundary conditions in all three physical domains (mechanical, electrical, acoustical), and the mesh requirements for the three-dimensional analysis are summarized.

2.1. Materials

In the mechanical domain, the R19 pMUT materials have been defined in the following way: Mo is isotropic elastic, Si and SCAlN are anisotropic elastic and ScAlN is also linearly piezoelectric. For the first two materials, the elastic constants (Si) and the Young’s modulus (Mo) are extracted according to [16].

The Sc_0.15Al_0.85N parameters, i.e., the elastic constants and the piezoelectric coupling coefficients, are instead computed following the methodology reported in [17], with the values summarized in

Table 2. Material properties of Sc_0.15Al_0.85N, with $C_{66}={\displaystyle \frac{1}{2}}(C_{11}-C_{12})$.

Property	Value	Unit
Dielectric constant ${\epsilon }_{33}$	13.79	–
Mass density $\rho$	3.23	g/cm3
Piezoelectric coefficient $e_{31}$	−0.63	C/m2
Piezoelectric coefficient $e_{33}$	1.77	C/m2
Piezoelectric coefficient $e_{15}$	−0.29	C/m2
Elastic compliance $C_{11}$	348.97	GPa
Elastic compliance $C_{12}$	144.97	GPa
Elastic compliance $C_{13}$	119.68	GPa
Elastic compliance $C_{33}$	305.95	GPa
Elastic compliance $C_{44}$	104.82	GPa
Elastic compliance $C_{66}$	102.00	GPa

.

2.2. Boundary Conditions

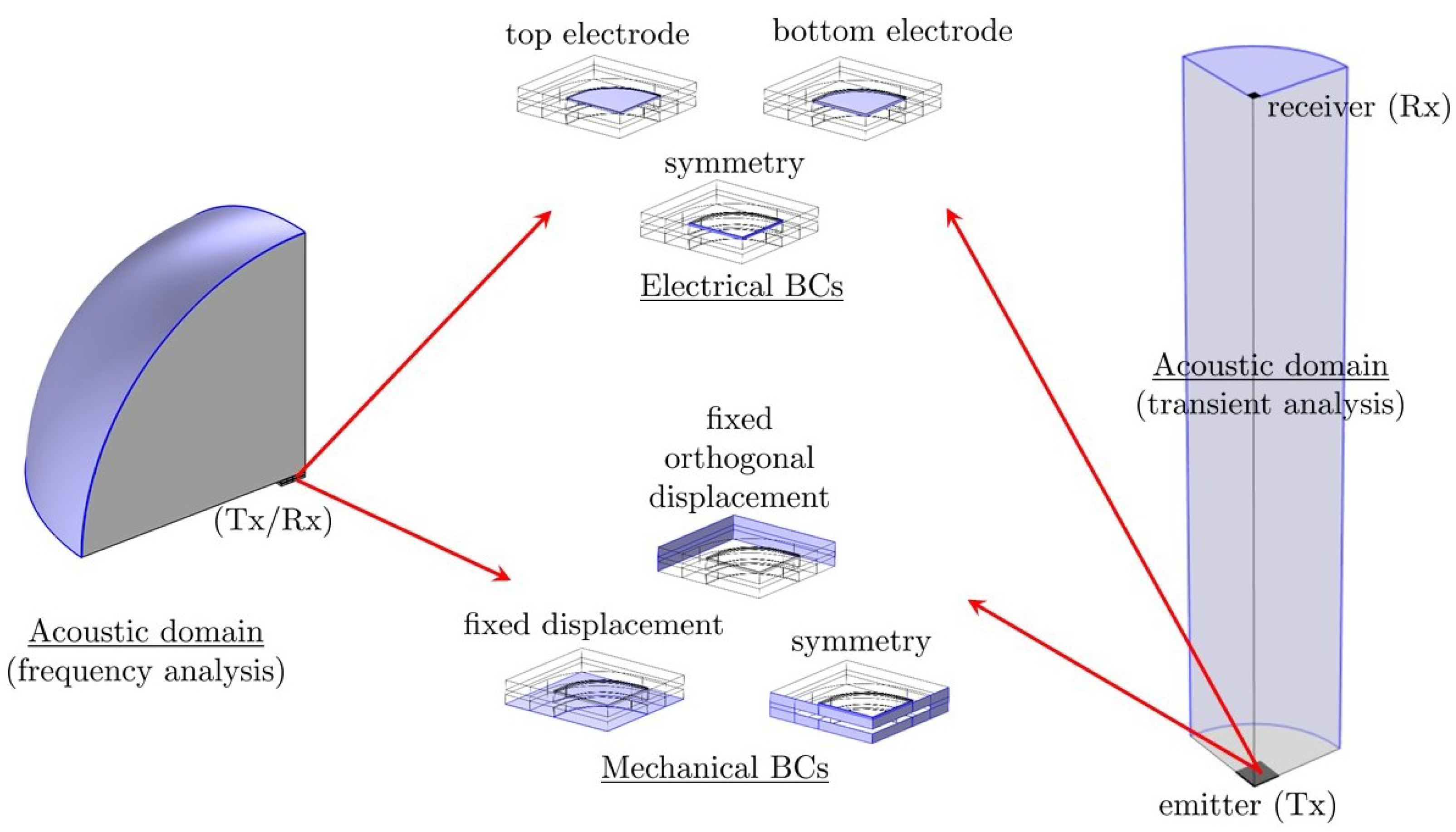
Two types of analysis were performed in the ballistic gel medium: frequency analysis and transient analysis.

In the first case, the acoustic domain has been approximated by a quarter sphere (see Figure 2 (left)), with the device located at the center of the sphere, receiving or emitting an acoustic wave. If the device is the Tx, a time-varying voltage is applied and the pressure spectrum generated at a certain distance in the fluid is recorded. If the device is the Rx, a time-varying sinusoidal pressure is applied to the top of the sphere and the effect on the device, i.e., voltage and energy per pressure unit, generated across the piezoelectric layer, is recorded.

In the transient analysis case, the acoustic domain is instead approximated by a quarter cylinder (see Figure 2 (right)).

In both cases, it is important to apply a spherical wave radiation condition on the outer (curved) surfaces to avoid spurious reflections of the acoustic wave. Moreover, symmetry is also exploited wherever possible in the mechanical and electrical domains (see Figure 2 (center)); the device base under the cavity is held fixed; the displacement components in directions perpendicular to the lateral surfaces that are not on the symmetry planes are set to zero; the bottom and top surfaces of the piezoelectric layer are kept at zero voltage or at varying sinusoidal voltage, respectively.

2.3. Meshing

To reduce the computational burden, in the mechanical domain only the piezoelectric layer has been discretized using three-dimensional, quadratic prismatic Lagrangian solid elements, while the other thin layers have been modeled using cubic (third-order) Lagrangian shell elements, according to the hybrid solid shell technique [18,19].

In the acoustic domain, tetrahedral quadratic Lagrangian elements are employed, with a maximum lateral size set to one-fifth of the acoustic wavelength. This meshing strategy ensures a spatial resolution of approximately 10 nodes per wavelength, which is sufficient for accurate wave propagation modeling. It is in fact very important to carefully design the mesh within the available memory and CPU power limits, since the fluid domain discretization can easily consume all computing resources: in the frequency domain simulations 190,467 elements and 499,429 degrees of freedom (dofs) were used, while in the transient analyses 410,104 elements and 756,605 dofs were used. The wall-clock time for the longest transient analyses amounted to about 10 h with a workstation Intel^® Xeon^® W-2275 CPU @ 3.30GHz and 128 GB RAM.

3. Frequency Domain Analysis in Ballistic Gel

The eigen-frequency analysis considers all coupled domains. First, the focus is on the Tx, where a pMUT array is considered to achieve a relevant pressure wave amplitude at regime. Then, the analysis moves to the Rx, for which, in the case of the R19 device, the single configuration and the 2 × 2 array (giving a 100 × 100 µm² footprint) are compared.

3.1. Transmit Sensitivity of the 8 × 8 R19 Array

In this work, it is conventionally assumed that the frequency response function of an array is computed as the average center displacement of the individual membranes. This approach actually implies that all pMUT elements are actuated simultaneously and in phase and that the excitation is spatially uniform across the array. The last hypothesis is actually challenged by the interaction between pMUTs, which causes nonlinear mechanical vibrations, and acoustic cross-talk. The resonance peak shifts from 11.04 MHz for a single pMUT (not represented here) to 14.0 MHz for the 8 × 8 array, see Figure 3. This shift is primarily attributed to cross-talk phenomena, where mutual interactions between adjacent pMUT elements influence the overall dynamic behavior of the array (stiffening effect).

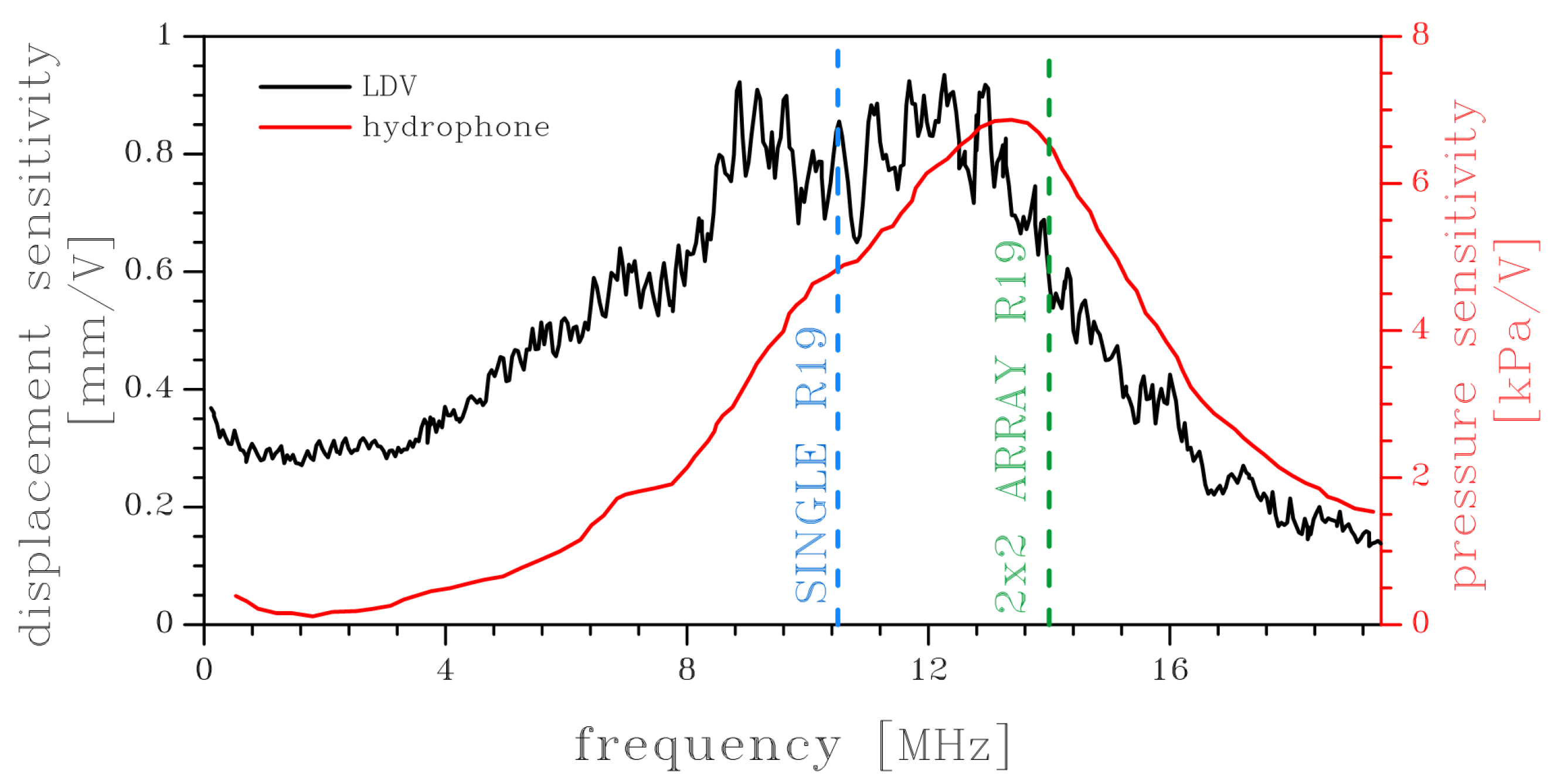
The obtained fundamental frequency is comparable with the experimental results shown in [14] for a larger 50 × 55 R19 array. In Figure 4, in particular, the numerical resonance frequencies of the fundamental mode for a single R19 (in blue) and for a 2 × 2 R19 array (in green) are indicated by dashed lines. The experimental measurements were carried out by using laser Doppler vibrometry (LDV, black line) and by a hydrophone (red line) that was placed at a distance of 20 mm in water. Although the dimensions of the measured array are much larger than those studied by numerical simulations, the results are encouraging when considering that the medium has a comparable velocity of propagation.

3.2. Receiving Sensitivity of a Single R19 Device and of a 2 × 2 R19 Array

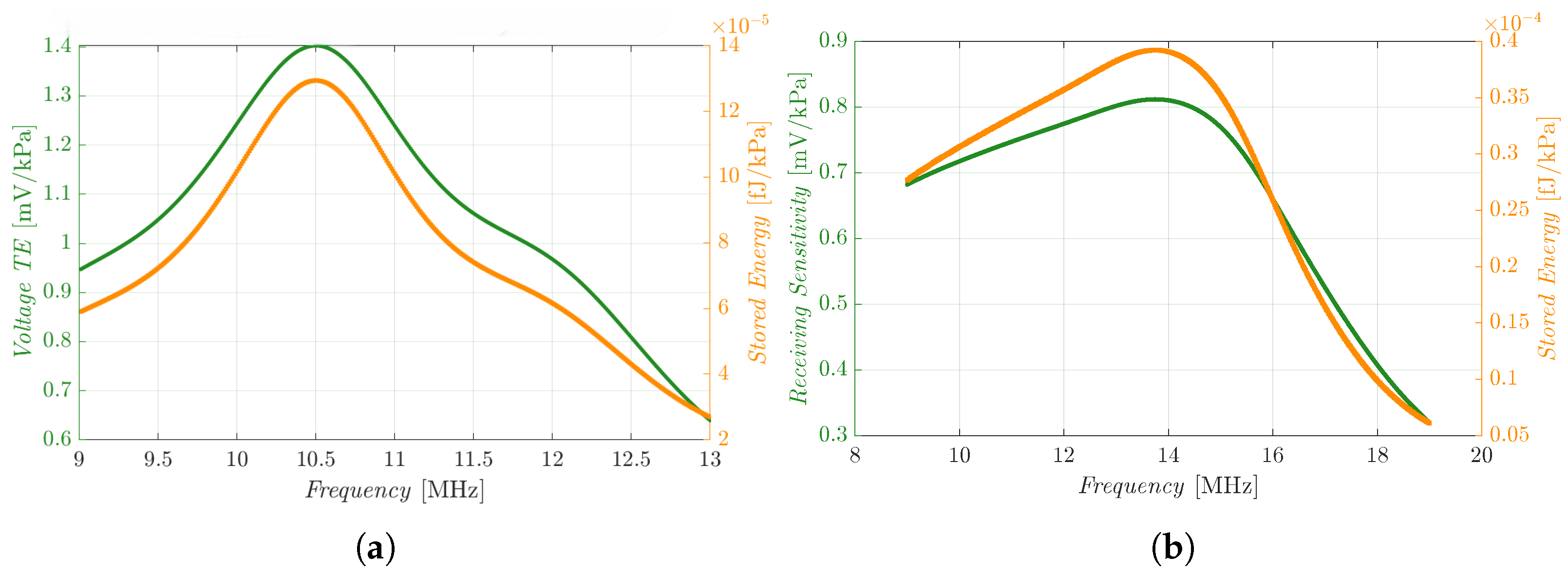
As depicted in Figure 5a, when the single R19 pMUT is deformed by an acoustic wave traveling in ballistic gel with an amplitude of 1 kPa at 10.5 MHz, due to the converse piezoelectric effect it generates an AC voltage amplitude of about $1.4\mathrm{mV}$ on the top electrode, while the piezoelectric layer produces an energy peak of $1.25\times {10}^{-4}\mathrm{fJ}$.

When the 2 × 2 array is instead deformed by the same acoustic wave, each element generates a $0.8\mathrm{mV}$-amplitude voltage and stores energy with a $0.4\times {10}^{-4}\mathrm{fJ}$ peak ($1.6\times {10}^{-4}\mathrm{fJ}$ if we consider the whole array). The cross-talk effect of the array can be observed, as the generated voltage is decreased with respect to the single device. On the other hand, by connecting the four pMUTs in parallel, it is possible to harvest more energy and power, and also reduce the overall impedance.

Several aspects must be considered to define the optimal set-up for energy harvesting, specifically regarding the operational frequencies of the two device configurations:

• The 2 × 2 array allows for better resonance frequency matching with the Tx, as both are affected by stiffening effects that cause a frequency shift. Better matching provides lower losses in the transmit sensitivity (the operational frequency is always set to the resonance of the Rx);
• Higher operational frequency (2 × 2 array case) brings higher collected power, this term being dependent on the frequency, which is ideal for energy harvesting;
• However, the ballistic gel attenuation must be considered for our analysis. This term also depends on the operational frequency, meaning that, in the case of a single R19 as Rx, there will be less attenuation and consequently reduced losses in the acoustic pressure, see also the discussion in the next Section;
• Spatial peak temporal average intensity must be checked in order to respect the safety limits on ultrasound waves imposed by the United States Food and Drug Administration (FDA). On this topic, a lower transmit power, given by a higher frequency shift between Tx and Rx (single pMUT case), may be ideal to not surpass the FDA safety limits;
• In case the electrical signal must be delivered back from the Rx to the Tx, the 2 × 2 array seems more ideal for this purpose, because it brings more transmit power and it is better matched with the Tx.

As some points mentioned above contradict each other, a time domain analysis, described in the following Section, is also carried out. It will provide a detailed insight into all these topics in order to find the optimal configuration for our purpose.

4. Time Domain Analysis

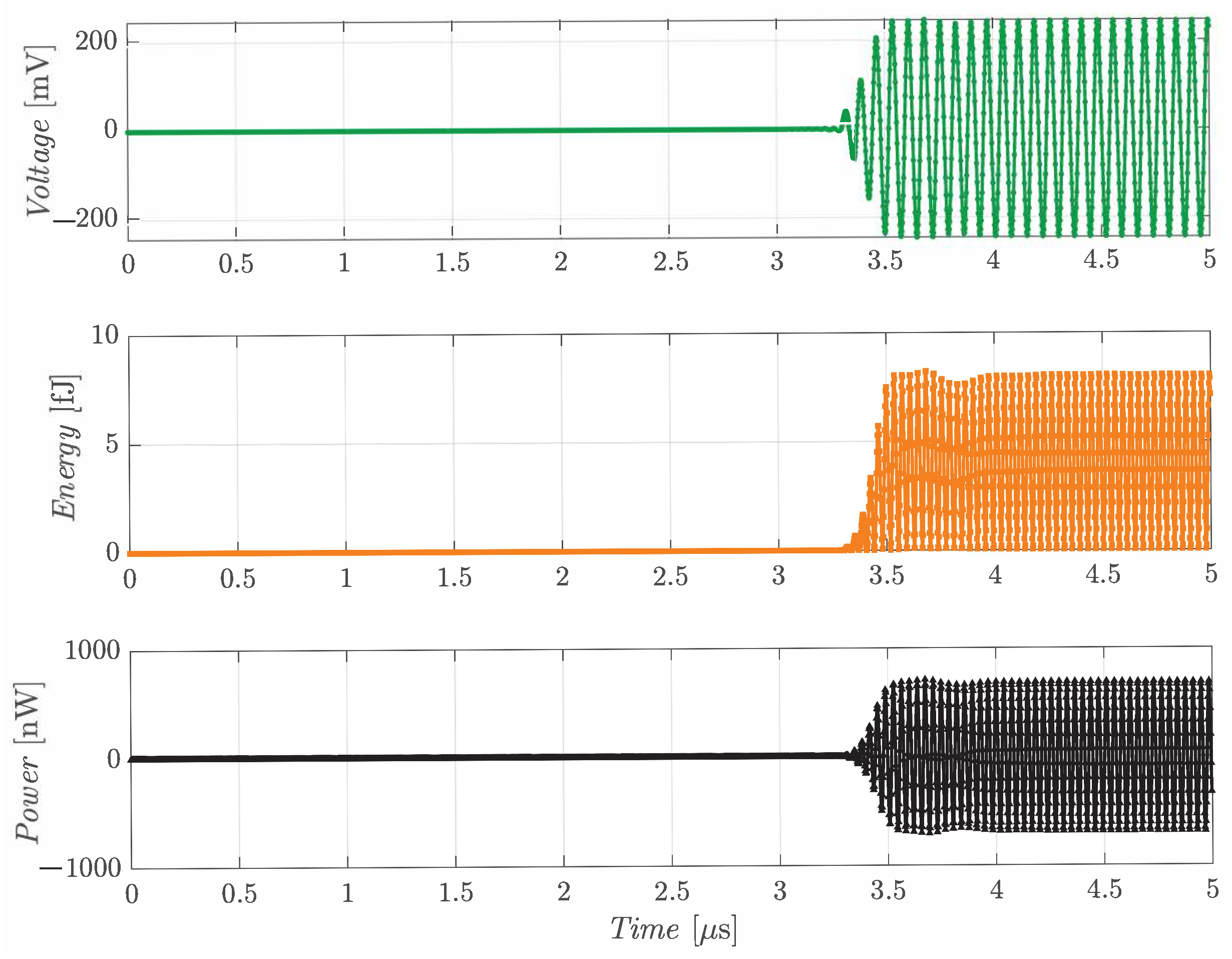
The time domain analysis was carried out for the single R19 device and for the 2 × 2 array by placing the Tx and the Rx at a distance of 5 mm in the ballistic gel medium. A sinusoidal voltage, with 20 V amplitude and frequency equal to the Rx resonance, was applied to the 8 × 8 array working as Tx, driving each element in phase. The analysis was conducted for 5 µs.

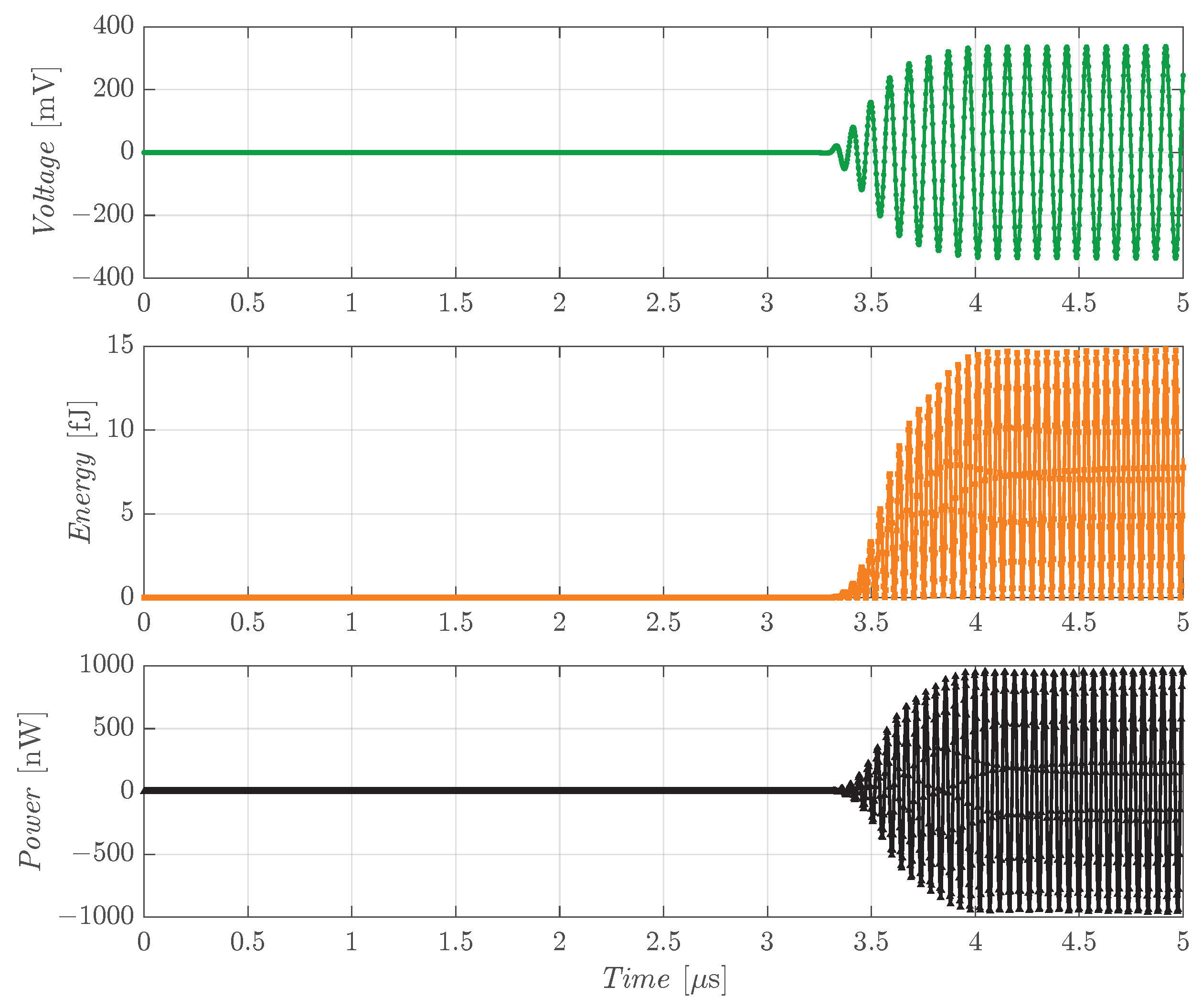
Figure 6 shows the results obtained, in terms of voltage, energy and power, when the 2 × 2 array is used as the Rx. Considering the ballistic gel speed of sound and the distance between the two devices, the acoustic wave is expected to reach the Rx after 3.16 µs, consistent with what is depicted in the plots. The same analysis was repeated for the single R19 used as Rx, with the results depicted in Figure 7. The peak values of the electrical parameters at steady-state are summarized in

Table 3. Extracted electrical performance from the transient simulation for the single R19 and the 2 × 2 array. In the latter case, a parallel connection between each element is considered.

Quantity	Symbol	Single R19	2 × 2 Array	Unit
Voltage	$V_{\mathrm{peak}}$	337	213	mV
Energy	$E_{\mathrm{peak}}$	15	32.2	fJ
Power	$P_{\mathrm{peak}}$	0.96	2.74	µW

.

Comparing the two voltage plots in Figure 6 and Figure 7, it can be observed that the single R19 is able to collect a higher voltage, suggesting that the cross-talk effect of the 2 × 2 array brings a larger voltage drop compared to the frequency shift of the single device. The large bandwidth of the R19 in ballistic gel (∼4 MHz in the 8 × 8 array) facilitates operation at lower frequencies without considerable losses in the acoustic pressure. The two plots also evidence that the connection of four pMUTs in parallel enables a larger total stored energy. From these assumptions, it can be stated that the optimal configuration for the Rx initially depends on what is considered more fundamental for the target application, either voltage or electrical power. However, further aspects must be taken into account to find the ideal implementation that will be analyzed in detail in the following subsection.

4.1. Output Power

The instantaneous output collected power is a crucial parameter for energy harvesting applications and can be computed as

$$P\left(t\right)={\displaystyle \frac{dE\left(t\right)}{dt}},$$

indicating that it is directly dependent on the stored energy. More precisely, power can be approximated, starting from the energy formula $E\left(t\right)\approx {\displaystyle \frac{1}{2}}{C}_{0}V{\left(t\right)}^2$, in the following way:

$$P\left(t\right)\propto C_0{V}^2{\omega }_0,$$

(1)

where $C_0$ is the capacitance of the piezoelectric layer at rest, V is the voltage amplitude detected and ${\omega }_0$ is the angular resonance frequency. The above equation proves that both energy and power depend on $C_0$ (and therefore on the area and thickness of the piezoelectric layer) and $V\left(t\right)$, while the latter term also depends on the fundamental frequency $f_0={\displaystyle \frac{{\omega }_0}{2\pi }}$. As a consequence, the 2 × 2 array provides even more output power, having a higher working frequency combined with the additional factor 4 given by the parallel connection. It must be specified that the formulae presented are an approximation of energy and power and are only used to demonstrate their dependence on voltage and frequency.

4.2. Time to Reach the Steady-State Condition

Another fundamental advantage of a higher resonance frequency lies in the settling time, which leads to increased operating speed. Indeed, by assuming the mechanical vibration of the membrane as that of a linear resonator, its time constant can be derived as

$$\tau ={\displaystyle \frac{2Q}{{\omega }_0}},$$

where Q is the quality factor. The time constant defines the steady-state condition (∼5$\tau$), meaning that the 2 × 2 array will have a shorter settling time. Additionally, the array also presents a larger bandwidth compared to the single device, which leads to a lower quality factor, further reducing the settling time and, consequently, enabling faster operation for the 2 × 2 array Rx.

4.3. Ballistic Gel Attenuation

Despite the advantages, higher working frequencies bring several drawbacks. A crucial one is the ballistic gel attenuation, which can be expressed as

$$\mathrm{Attenuation}\left(\mathrm{dB}\right)=\alpha ·f_0·d,$$

(2)

where $\alpha$ is the acoustic attenuation coefficient, set to $\alpha =1.07\mathrm{dB}/\mathrm{MHz}·\mathrm{cm}$ [15], and d is the distance, in centimeters, from the acoustic source. Since both Rxs operate at significant high frequencies (>10 MHz), the pressure losses caused by the acoustic attenuation will be substantial, with a slightly larger dissipation in the 2 × 2 array.

As a first approximation, the pressure loss was estimated analytically using Equation (2) and converting the attenuation from dB to linear, obtaining 47.6$\%$ in the single R19 and 57$\%$ in the 2 × 2 array case.

The peak values obtained by applying the respective reduction factors are reported in

Table 4. Extracted electrical performance of the two Rxs when the ballistic gel acoustic attenuation is applied.

Quantity	Symbol	Single R19	2 × 2 Array	Unit
Voltage	$V_{\mathrm{peak}}$	176.6	91.6	mV
Energy	$E_{\mathrm{peak}}$	4.11	5.95	fJ
Power	$P_{\mathrm{peak}}$	264	507	nW

.

4.4. Spatial Peak Temporal Average Intensity

As described in the previous section, the FDA has established an exposure limit to ultrasound waves in the medical field, specifically 7.2 $\mathrm{mW}/{\mathrm{mm}}^2$ [20]. To check whether an experimental setup respects the defined safety limits, the Spatial Peak Temporal Average Intensity $I_{\mathrm{SPTA}}$ is computed at the point of maximum intensity [12]:

$$I_{\mathrm{SPTA}}={\displaystyle \frac{p_{peak}^2}{2\rho c}}·C,$$

(3)

where $p_{peak}$ is the measured peak acoustic pressure, C is the duty cycle and c, $\rho$ are the ballistic gel speed of sound and density, respectively. The $I_{\mathrm{SPTA}}$ is practically defined as the ratio between the acoustic power ${\displaystyle \frac{p_{peak}^2}{2}}$ and the acoustic impedance $Z_a=\rho c$, multiplied by the signal duty cycle. The point of maximum intensity was selected based on the Rayleigh distance, which establishes when the acoustic signal enters the far-field region and becomes stable. The Rayleigh distance Z is computed as follows [13]:

$$Z={\displaystyle \frac{a^2}{\lambda }},$$

(4)

where a is the Tx radius and $\lambda$ is the acoustic signal wavelength. Considering the 8 × 8 array Tx, where the radius a is evaluated as $a={\displaystyle \frac{7L_{pitch}}{2}}=175\mathsf{\mu }\mathrm{m}$, the Rayleigh distance turns out to be $Z=210\mathsf{\mu }\mathrm{m}$ and $Z=273\mathsf{\mu }\mathrm{m}$ for the single device case and the 2 × 2 array, respectively.

Based on the computed values, the maximum intensity point was chosen at a distance of 500 $\mathsf{\mu }\mathrm{m}$ from the Tx, ensuring that the acoustic signal is completely stable. To evaluate the maximum $I_{\mathrm{SPTA}}$, the acoustic pressure at the selected point was measured in both cases during the transient analysis, obtaining the time-dependent plots depicted in Figure 8.

Since the two Rxs work at different frequencies, the emitted pressure of the 8 × 8 array will be different in the two case studies, with a higher acoustic pressure in the 2 × 2 array case as its resonance frequency is closer to the one for the Tx. As a result, it was measured a peak pressure of 277 and 531 kPa, corresponding to an $I_{\mathrm{SPTA}}$ of 23.5 and 86.5 $\mathrm{mW}/{\mathrm{mm}}^2$, respectively, above the FDA exposure limit. To solve this issue, a duty cycle C must be added to the driving input signal, namely 30% in the single R19 and 8% in the 2 × 2 array case.

The main drawback of the introduction of a duty cycle is the reduction in the average output collected energy, which decreases proportionally to C. Instead, the instantaneous power that was measured during the transient analysis is not affected by the duty cycle, resulting in an unchanged power peak. Considering the average energy and the voltage amplitude, the single R19 device appears to be more advantageous in this regard, as it delivers a higher output compared to the 2 × 2 array. Conversely, looking at the instantaneous power, the 2 × 2 array performs better. More accurate numerical simulations, including the addition of a resistive load, will be conducted in the future to evaluate the average harvested power and quantify the reduction introduced by the duty cycle.

5. Conclusions

In this work, a pMUT device that exists in the literature was studied as a harvester to provide wireless energy transmission to a biosensor through multi-physics three-dimensional simulations. Unlike previous studies, the present work pursued the possibility of using high frequencies (>10 MHz) and a very small footprint (100 × 100 µm²). The analyses reported here propose a comparison between a single device and a 2 × 2 array for the receiver, both powered by an 8 × 8 array at a distance of 5 mm in a ballistic gel medium that mimics human internal organs.

By combining frequency-response and transient analyses while accounting for acoustic dissipation phenomena, this study underscores the necessity for a trade-off between the single device and the array solution for the receiver: the former provides a higher voltage amplitude at steady-state, while the latter provides a higher instantaneous power. The single device performances, in particular, appear in line with digital nano-electronics requirements, but a duty cycle must also be accounted for. The chosen material, ScAlN, replaces the more common PZT, which performs better under the same conditions; however, ScAlN guarantees better bio-compatibility and CMOS-integration. In addition, common PZT pMUT geometries [18] work at lower frequencies (1–5 MHz), where attenuation is significantly reduced. Ongoing work is exploring alternative but slightly larger geometries that could achieve a good performance balance to have a precise comparison with PZT pMUTs in energy harvesting capabilities.