Backstepping-Based Trajectory Control for a Three-Rotor UAV: A Nonlinear Approach for Stable and Precise Flight ^†

Abstract

Ensuring precise trajectory tracking and stability in unconventional UAVs is a critical challenge in aerial robotics. This paper investigates a three-rotor UAV with complex underactuated dynamics and develops a nonlinear backstepping controller. The UAV model highlights the essential role of onboard sensors, since position and angular velocity measurements are fundamental for feedback and must be continuously exploited by the control law. Using these sensor-based signals in simulation, the proposed controller achieves accurate trajectory tracking, fast convergence, and stable behavior. The study emphasizes that sensor integration is crucial for enabling reliable autonomous flight of unconventional UAVs.

1. Introduction

The increasing demand for agile and versatile aerial platforms has driven significant research into novel UAV configurations. Among them, tilt tri-rotor UAVs offer a promising compromise between maneuverability and endurance. However, their asymmetric structure and nonlinear dynamics pose major control challenges.

To ensure stable hovering, a sliding mode control SMC with a disturbance observer and control allocation was proposed in [1], while smooth transition between flight modes was addressed via a cascade controller in [2]. A feedback linearization strategy combined with PID control (tuned by genetic algorithms) enabled accurate trajectory tracking for a T-shaped tri-copter in [3]. A flying-wing tilt three-rotor equipped with a mechanical tilting mechanism and controlled by classical PID was validated through flight tests in [4]. Comparative simulations using PID and LQG controllers were also performed to assess trajectory tracking accuracy in [5]. In terms of design, a hybrid Vertical Take-Off and Landing (VTOL) UAV with thrust vectoring and minimal actuation was proposed in [6], and an improved aerodynamic modeling technique coupling Computational Fluid Dynamics (CFD) and multibody dynamics was introduced in [7]. Simpler architectures using fixed-pitch propellers and speed variation for control were explored in [8]. Robustness against actuator failures was investigated in [9], where dynamic control allocation exploited system redundancy to maintain stable flight. A lightweight tri-rotor configuration with asymmetric thrust distribution and onboard combustion engine was tested in [10].

Recent works focus on enhancing the robustness and control of tri-rotor UAVs. An ADRC-based control for smooth mode transition in a composite tilt-rotor UAV was proposed and validated through simulations in [11]. A quaternion-based dynamic model for tri-copters was developed in [12] to enable accurate, singularity-free attitude control. A fault-tolerant controller [13] using a super-twisting observer and RISE method showed effective compensation under actuator faults. A fully actuated planar tri-copter enabling inclined hovering was introduced in [14] with nonlinear attitude tracking control. Sliding Mode Control has been used in [15] to stabilize tilt tri-rotor UAVs in hover, showing strong robustness against disturbances. Finally, PID tuning via optimization was proposed in [16] to improve tracking accuracy in programmed 3-rotor UAV flights.

The backstepping control approach has been widely adopted to enhance robustness and precision across various robotic systems [17]. For quadrotors, it enables accurate trajectory tracking even under wind disturbances, especially when combined with optimization-based tuning [18]. In the domain of wheeled mobile robots, backstepping has been effectively used to ensure energy-efficient motion and precise trajectory tracking with minimal control effort [19]. Furthermore, in the control of autonomous helicopters, backstepping coupled with disturbance observers provides agile attitude tracking and strong disturbance rejection capabilities, particularly in uncertain and outdoor environments [20]. In this study, a nonlinear controller based on the backstepping technique is proposed for trajectory tracking of a three-rotor UAV. The main contributions include the development of a comprehensive nonlinear dynamic model specific to the three-rotor configuration, the design of a control law that effectively handles system nonlinearities, and the validation of the proposed strategy through realistic simulation scenarios demonstrating stable and precise trajectory tracking performance.

Table 1. Assessment of the proposed approach with respect to state-of-the-art solutions.

Ref.	Approach	Features	Limitations	Novelty
[21]	Fuzzy backstepping and sliding mode	Attitude and altitude stabilization; fuzzy logic	Hybrid; no 3D trajectory	-
[22]	Maneuvering control via backstepping	Backstepping for maneuvering	Comparative assessment, not Lyapunov trajectory control	-
[23]	PID vs backstepping	Comparative study	Simulation only	-
This work	Nonlinear backstepping trajectory control	Lyapunov proof; sensor-based; complex trajectories	Simulation only	1st pure backstepping-based trajectory controller for underactuated three-rotor UAV

highlights the novelty of this paper with respect to the other state-of-the-art backstepping controllers for 3-rotor UAVs [21,22,23].

To the best extent of our knowledge, prior three-rotor backstepping studies are limited to hybrid fuzzy/SMC backstepping designs, maneuvering and attitude control, or fully actuated tilt variants. In contrast, this paper proposes a Lyapunov-based backstepping trajectory-tracking controller specific to the triangular three-rotor geometry, using only standard onboard measurable signals. The proposed backstepping controller relies on signals that are directly measurable with standard onboard sensors. All the states in the controller (attitude, angular rates, and position) can be obtained from inertial measurement units, magnetometers, GPS, etc. As such, the proposed control strategy is both scientifically sound and practically deployable on real-world 3-rotor UAVs. By grounding the controller design in measurable feedback signals, the work aligns with sensor-driven UAV applications and bridges the gap between control theory and practical 3-rotor UAV sensing, enabling stable and precise trajectory tracking. This paper is organized as follows. Section 2 introduces the mathematical model of the UAV, while Section 3 presents the backstepping control design. Section 4 discusses the simulation results and evaluates the controller’s effectiveness. Section 5 concludes the study with final remarks and suggestions for future work.

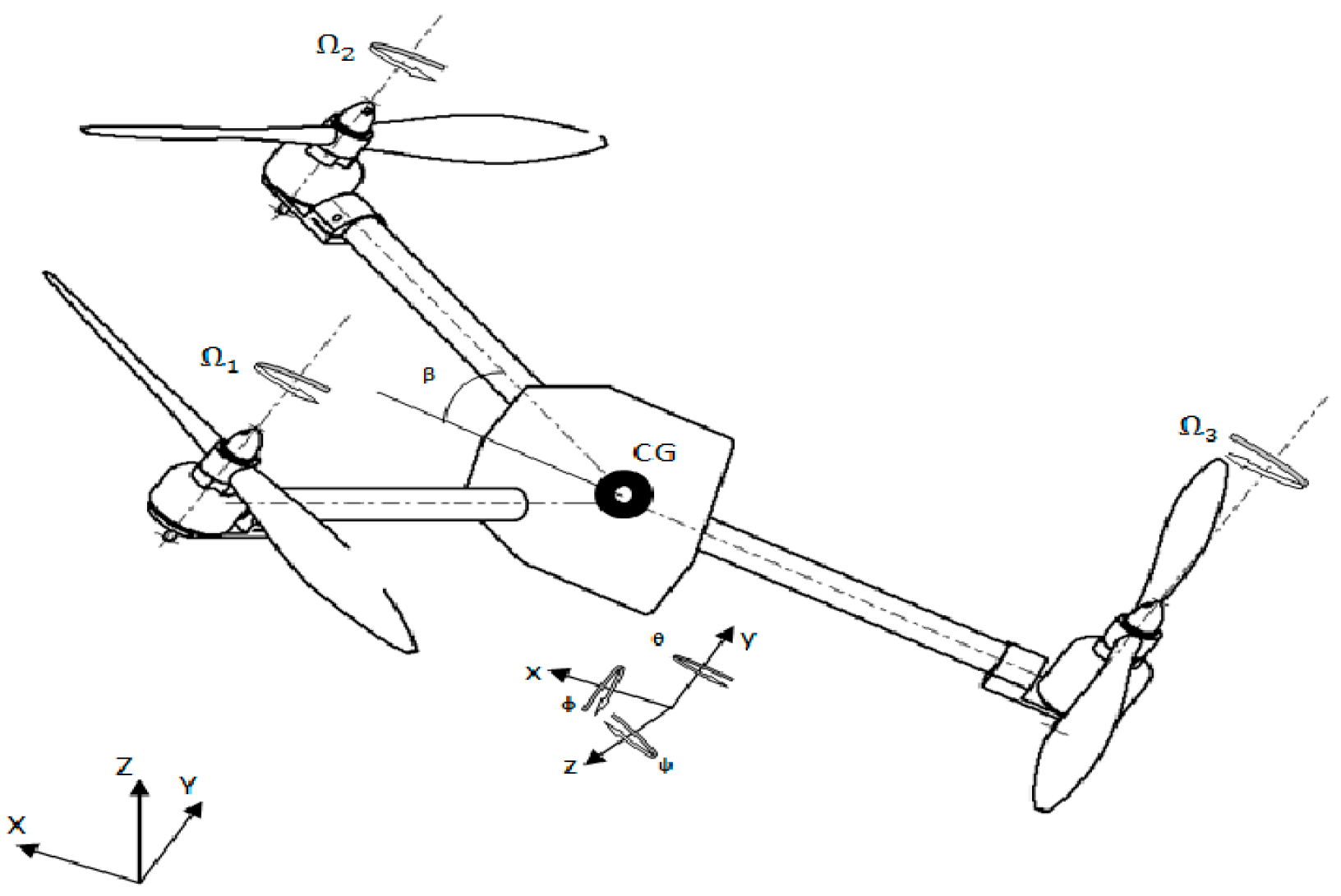
2. System Model

The UAV considered in this work is a simplified three-rotor system, characterized by three rotors arranged symmetrically in a triangular configuration. The center of mass is assumed to coincide with the geometric center of the platform, which is schematically represented in Figure 1.

To develop a comprehensive dynamic model that accurately reflects the behavior of the tri-rotor UAV, we introduce the following assumptions to simplify the analysis by concentrating on the most significant factors:

• The UAV is a rigid body.
• The aerodynamic drag and gyroscopic effects are neglected.
• The thrust produced by each rotor is proportional to the square of its angular velocity.
• The system operates under small to moderate angular displacements (<30°) to ensure the validity of the control model.

The modeling of the three-rotor UAV is essential to design an appropriate nonlinear controller that ensures stable trajectory tracking. This section presents the dynamic equations governing the UAV’s translational and rotational motion.

2.1. Definition of States

The motion of the three-rotor UAV is described by six variables:

• x, y, z: the position coordinates of the UAV in space.
• ϕ: the roll angle, representing the inclination of the UAV along the longitudinal axis.
• θ: the pitch angle, representing the inclination along the lateral axis.
• ψ: the yaw angle, representing the heading.

These variables, along with their time derivatives, define the dynamic state of the UAV and are used to express both the translational and rotational motion in the next sections.

2.2. Translational Dynamics

Let $(x,y,z)$ be the UAV’s position in the inertial frame, and let $m$ be the total mass of the vehicle. The translational dynamics are described by Newton’s second law:

$$\{\begin{array}{c}\ddot{x} = {\displaystyle \frac{T}{m}}(cos\varphi sin\theta cos\psi +sin\varphi sin\psi )\\ \ddot{y} = {\displaystyle \frac{T}{m}}(cos\varphi sin\theta cos\psi -sin\varphi sin\psi )\\ \ddot{z} = -{\displaystyle \frac{T}{m}}cos\varphi cos\theta +g\end{array}$$

(1)

where $T$ is the total thrust generated by the three rotors and $g$ is the gravitational acceleration.

These equations are consistent with the block structure implemented in Simulink for trajectory tracking in the $(x,y,z)$ directions.

2.3. Rotational Dynamics

Let $I_x$, $I_y$ and $I_z$ be the moments of inertia around the roll, pitch, and yaw axes, respectively. The rotational dynamics of the UAV are given by:

$$\{\begin{array}{c}{I}_x\ddot{\varphi }={\tau }_{\varphi }\\ I_y\ddot{\theta }={\tau }_{\theta }\\ I_z\ddot{\psi }={\tau }_{\psi }\end{array}$$

(2)

where ${\tau }_{\varphi }$, ${\tau }_{\theta }$ and ${\tau }_{\psi }$ are the control torques generated by the differential speeds of the rotors. These torques are considered as inputs in the control loop and are computed in the next section using a backstepping strategy.

2.4. State Vector and Control Inputs

The complete state vector of the system is defined as:

$$\left[x y z \varphi \theta \psi \ddot{x} \ddot{y} \ddot{z} \ddot{\varphi } \ddot{\theta } \ddot{\psi }\right]$$

(3)

The control inputs are defined as:

$${U=\left[\begin{array}{cccc}T& {\tau }_{\varphi }& {\tau }_{\theta }& {\tau }_{\psi }\end{array}\right]}^T$$

(4)

This state-space representation is used to derive the backstepping control laws for tracking the desired trajectory $\left[x_d\left(t\right),y_d\left(t\right),z_d\left(t\right),{\psi }_d\left(t\right)\right]$.

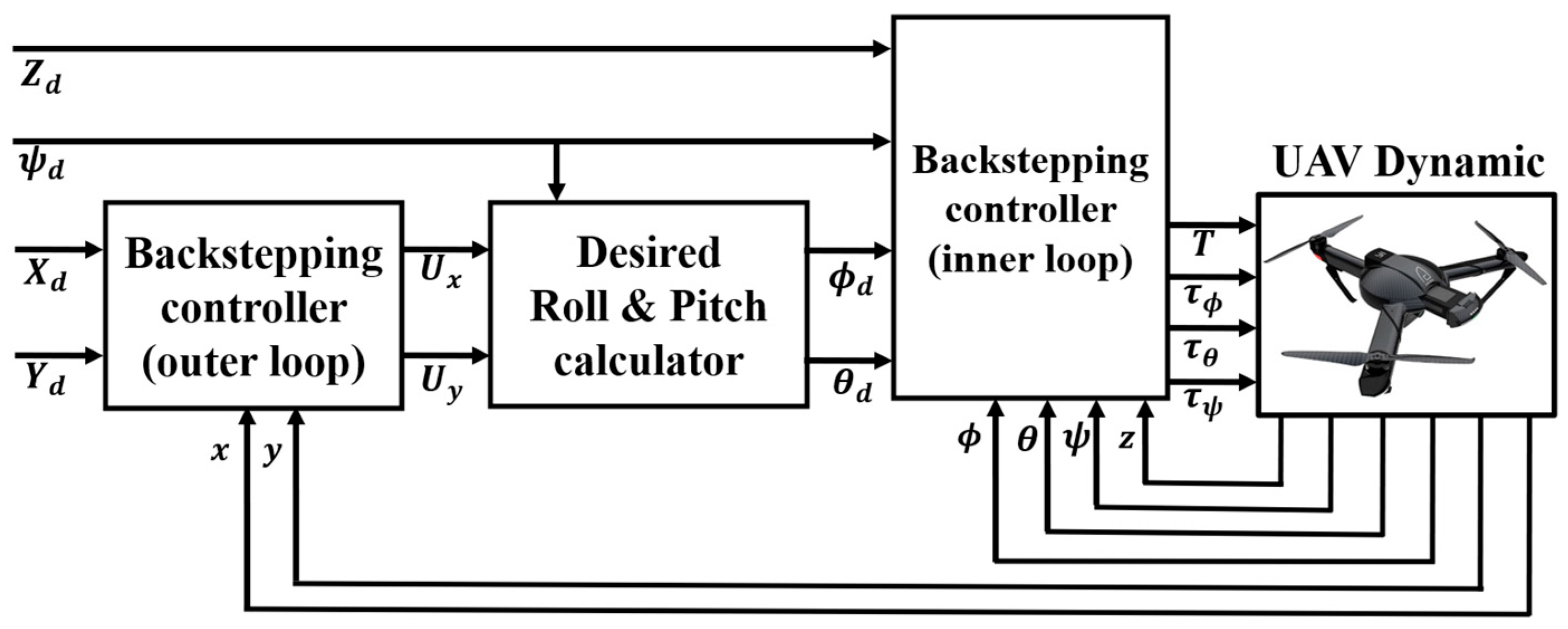
3. Control System

To ensure stable trajectory tracking of the three-rotor UAV, a nonlinear backstepping control approach is adopted. The controller is designed to guarantee asymptotic convergence of the position and orientation errors (Figure 2). The derivation of the control laws is based on Lyapunov stability theory. We begin by developing the vertical control law in detail.

3.1. Vertical Position Control

The vertical dynamics of the UAV are governed by:

$$\ddot{z}=-{\displaystyle \frac{T}{m}}cos\varphi cos\theta +g$$

(5)

We define the tracking error and its derivative as:

$$e_z=z_d-z, { \dot{e}}_z={\dot{z}}_d-\dot{z}$$

(6)

We consider the following Lyapunov candidate function:

$$V_z={\displaystyle \frac{1}{2}}{e_z}^2+{\displaystyle \frac{1}{2}}{{\dot{e}}_z}^2$$

(7)

Its time derivative is:

$${\dot{V}}_z=e_z{\dot{e}}_z+{\dot{e}}_z({\ddot{z}}_d-\ddot{z})$$

(8)

To ensure ${\dot{V}}_z<0$, we define the virtual control input $U_z$ as:

$${U_z={\ddot{z}}_d+\lambda }_z{\dot{e}}_z+k_z{e}_z\mathrm{with} k_z>0 \mathrm{and} {\lambda }_z>0$$

(9)

Assuming ideal tracking where $\ddot{z}=U_z$, the stability of the vertical subsystem is ensured. Substituting this into the UAV’s dynamics yields the final thrust command:

$$T={\displaystyle \frac{m\left({g-U}_z\right)}{cos\varphi cos\theta }}={\displaystyle \frac{m(g-{{\ddot{z}}_d-\lambda }_z{\dot{e}}_z-k_z{e}_z)}{cos\varphi cos\theta }}$$

(10)

3.2. Position and Attitude Control Laws

The virtual control inputs for position tracking in the horizontal plane are defined as:

$$\{\begin{array}{c}{U}_x={\ddot{x}}_d+{\lambda }_x{\dot{e}}_x+k_x{e}_x\\ U_y={\ddot{y}}_d+{\lambda }_y{\dot{e}}_y+k_y{e}_y\end{array}$$

(11)

The corresponding desired roll and pitch angles are obtained as:

$$\{\begin{array}{c}{\varphi }_d={\displaystyle \frac{1}{g}}(U_{x}sin\psi +U_{y}cos\psi )\\ {\theta }_d={\displaystyle \frac{1}{g}}(U_{x}cos\psi -U_{y}sin\psi )\end{array}$$

(12)

The control torques for attitude tracking are given by:

$$\{\begin{array}{c}{\tau }_{\varphi }=I_x({\ddot{\varphi }}_d+{\lambda }_{\varphi }{\dot{e}}_{\varphi }+k_{\varphi }{e}_{\varphi })\\ {\tau }_{\theta }=I_y({\ddot{\theta }}_d+{\lambda }_{\theta }{\dot{e}}_{\theta }+k_{\theta }{e}_{\theta })\\ {\tau }_{\psi }=I_z({\ddot{\psi }}_d+{\lambda }_{\psi }{\dot{e}}_{\psi }+k_{\psi }{e}_{\psi })\end{array}$$

(13)

With all gains $k_i>0$ and ${\lambda }_i>0$.

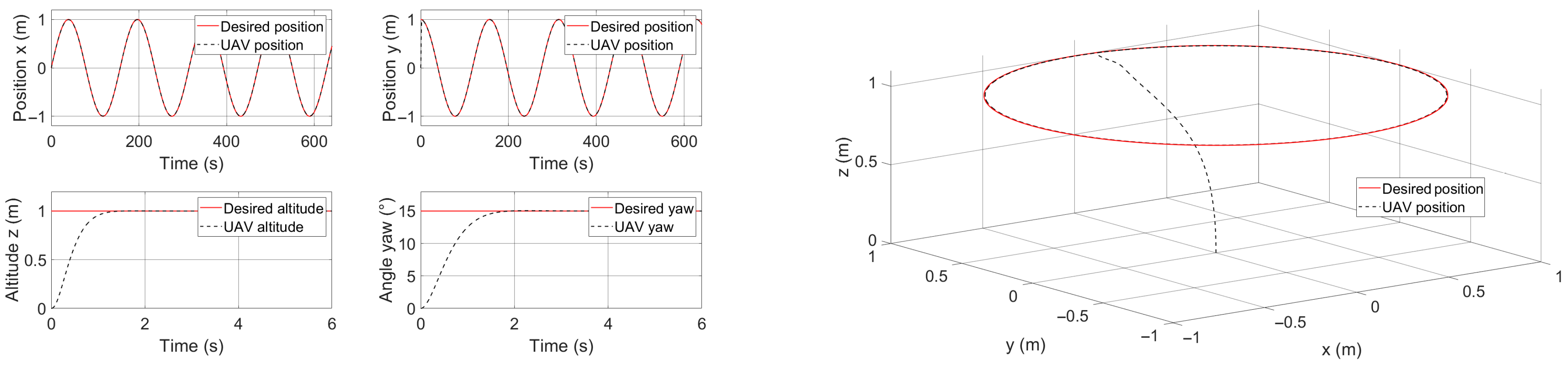
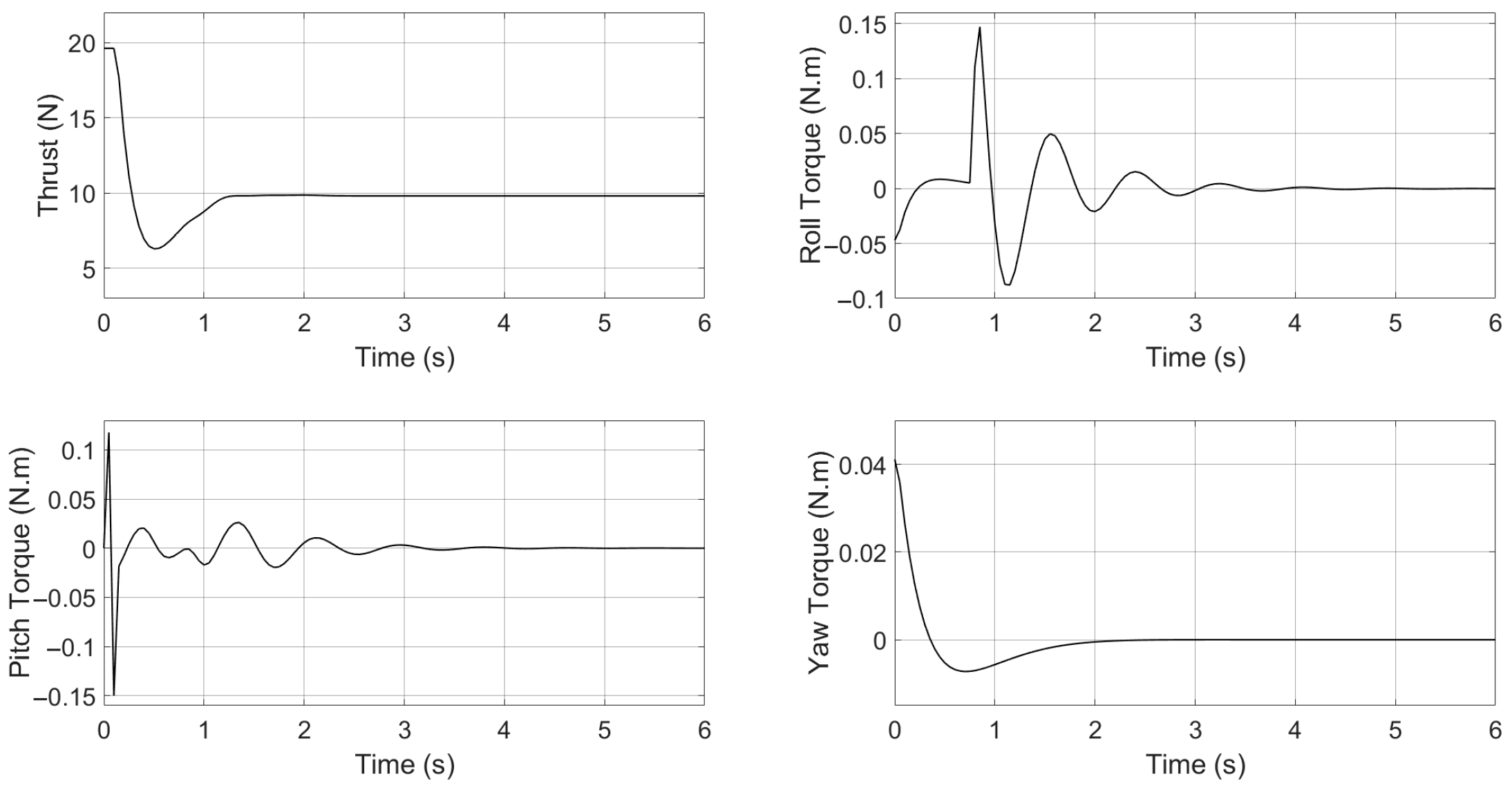
4. Results and Discussion

To assess the performance of the proposed backstepping-based control approach, two simulation scenarios were conducted using MATLAB/Simulink 2018a: a circular trajectory and a lemniscate trajectory. For each case, the UAV’s tracking accuracy, control efforts, and 3D motion are analyzed.

4.1. Scenario 1: Circular Trajectory

In the first scenario, the UAV was tasked with tracking a circular path in the horizontal plane while maintaining a constant altitude and yaw angle. The simulation results clearly demonstrate the ability of the controller to ensure stable and accurate flight.

The time response of the position components $x\left(t\right), y\left(t\right)$ and $z\left(t\right)$, along with the yaw angle $\psi$, confirms the ability of the proposed controller to accurately track different types of reference signals. In the circular trajectory scenario, the lateral position components $x$ and $y$ successfully follow sinusoidal reference signals with an amplitude of 1 m, which correspond to a circular path in the horizontal plane. The UAV exhibits smooth and synchronized tracking, with minimal phase lag and no steady-state error. The vertical position $z$ responds to a step reference of 1 m and quickly stabilizes around the desired altitude without overshoot or oscillation. Similarly, the yaw angle $\psi$ tracks a step reference of 15 degrees with fast convergence and good steady-state accuracy, confirming the effectiveness of the attitude regulation (Figure 3).

The 3D flight path generated during the simulation confirms the accurate reproduction of the circular trajectory. This demonstrates the capacity of the controller to manage rapid orientation changes and nonlinear couplings between position and attitude, while preserving tracking precision and flight stability (Figure 3).

Figure 4 shows the control efforts generated by the proposed controller during the circular trajectory scenario. The thrust exhibits a brief transient peak before converging to its steady hover value around 10 N. The roll and pitch torques remain very small (within ±0.15 N.m), with short oscillations during stabilization, while the yaw torque quickly decreases from about 0.04 N.m to nearly zero. After the initial transient, all control inputs settle smoothly, indicating stable attitude regulation with limited and well-damped actuation.

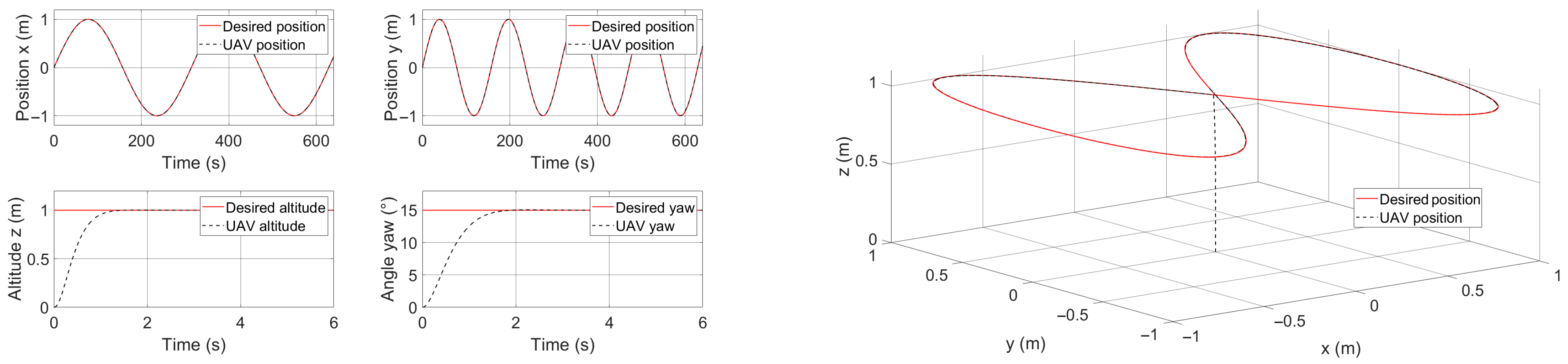
4.2. Second Scenario: Lemniscate Trajectory

The second scenario involves a more complex lemniscate trajectory, which imposes frequent curvature changes and directional inversions. This trajectory is particularly useful for evaluating the robustness and responsiveness of the controller under more demanding dynamic conditions.

In the lemniscate ($\infty$) trajectory scenario, the UAV is commanded to follow a figure-eight pattern generated by coupled sinusoidal references in the horizontal plane, each with an amplitude of 1 m. The position responses in $x\left(t\right)$ and $y\left(t\right)$ accurately replicate the oscillatory nature of the desired path, including the sharp curvature transitions and crossings at the center. The tracking is smooth, coordinated, and without noticeable lag or steady-state deviation. The altitude $z\left(t\right)$, commanded via a step input to 1 m, is well maintained throughout the trajectory, with fast convergence and stable behavior. Similarly, the yaw angle $\psi \left(t\right),$ driven by a step reference of 15 degrees, shows consistent tracking performance with rapid alignment and no overshoot, confirming that the attitude controller maintains orientation despite the high maneuverability demands of the lemniscate (Figure 5).

The 3D flight path generated during the simulation confirms the accurate reproduction of the lemniscate. The UAV smoothly transitions between the two lobes of the figure-eight shape without deviation or accumulation of error. This demonstrates the capacity of the controller to manage rapid orientation changes and nonlinear couplings between position and attitude, while preserving tracking precision and flight stability (Figure 5).

Figure 6 presents the control effort signals generated by the proposed controller during the lemniscate trajectory scenario. The total thrust shows an initial transient peak before converging to a steady value around 10 N. The roll and pitch torques remain very small (within approximately ±0.1 N.m) and exhibit short, well-damped oscillations caused by the rapid attitude adjustments required by the lemniscate motion. Similarly, the yaw torque decreases smoothly from about 0.04 N.m to nearly zero. Overall, the control inputs remain bounded and stable throughout the maneuver, confirming the controller’s ability to handle more complex trajectories with limited actuation effort.

Overall, the simulation results confirm the effectiveness and robustness of the proposed backstepping-based control strategy for trajectory tracking of a three-rotor UAV. The controller ensures smooth and stable tracking of both circular and lemniscate trajectories, even under nonlinear coupling between position and attitude. All tracking errors converge rapidly with minimal overshoot, and the control inputs remain bounded and physically consistent. These results validate the controller’s ability to handle complex reference trajectories while maintaining system stability.

As shown in

Table 2. Performance of the proposed controller with respect to other state-of-the-art results.

Control Method	Precision	Rapidity	Overshoot	Tested Trajectory	Limitations
PID [24]	Moderate	Low	>10%	Simple trajectory	Limited robustness and steady-state error
LQR [24]	Good	Moderate	0%	Simple trajectory	Requires linearization, limited for nonlinear systems
Sliding Mode Control [1]	High	Moderate	>3%	Square	Chattering phenomenon
Backstepping	High	Fast	0%	Circle & Lemniscate (complex sharp turns)	Requires a relatively complex design process

, conventional PID controllers are simple but suffer from steady-state errors and low robustness. LQR provides good results but depends strongly on linearization, which limits its use for nonlinear systems such as UAVs. Sliding Mode Control ensures high robustness but suffers from the well-known chattering phenomenon. In contrast, the proposed Backstepping control for the tri-rotor achieves zero error, fast response (settling time $\approx$ 1.2 s), and no overshoot, validated on both circular and complex lemniscate trajectories. The main limitation is the relative complexity of the controller design, but this is justified by the significant improvement in performance.

5. Conclusions

In this work, a nonlinear backstepping control approach was developed and applied to a three-rotor UAV to ensure stable and accurate trajectory tracking. The control design was derived step by step based on Lyapunov stability theory, ensuring asymptotic convergence of the position and attitude errors. The performance of the proposed method was evaluated through two representative scenarios involving circular and lemniscate trajectories. The simulation results demonstrated that the UAV is able to track the desired trajectories with high accuracy and without instability, even in the presence of sharp curvature and orientation transitions. The smooth evolution of the position and orientation, along with the physical consistency of the control inputs, confirms the applicability of this approach to real UAV systems. These findings are in line with recent trends in the literature, where nonlinear and Lyapunov-based methods, such as backstepping, have proven to be reliable and effective for UAV control. Moreover, since the controller relies solely on measurable signals, the study highlights the importance of considering the sensing capabilities of the UAV configuration when designing the flight control law. Future works may focus on addressing robustness to parametric uncertainties, wind gusts, and sensor noise.