Time-Frequency Analysis and Statistical Variation for Feature Extraction in the Dressing of Conventional Grinding Wheels ^†

Abstract

The study proposes a new methodology based on time-frequency analysis for the indirect monitoring of the dressing operation of conventional grinding wheels. Through a low-cost piezoelectric diaphragm (PZT), acoustic signals are captured during the process. The analysis is based on the coefficient of variation in the Short-Time Fourier Transform (STFT). The results indicate that the signal instability is high in the first passes but progressively decreases, reaching stability between passes 10 and 15. This suggests that the surface of the grinding wheel is regularized and ready for grinding. The methodology can serve as an objective indicator to assist the operator in interrupting the dressing process at the optimal moment, thereby optimizing grinding quality and reducing operational costs.

1. Introduction

Due to the high production demand and the need for optimization of mechanical processes, Tool Condition Monitoring (TCM) becomes extremely crucial in machining processes such as grinding. This process is responsible for the surface finishing of parts and is one of the last to be employed. The grinding tool is known as the grinding wheel, which is composed of abrasive grains bonded by a binder [1]. When the grinding wheel comes into contact with the workpiece, it performs a controlled surface cut, ensuring precision and final quality in production.

With the frequent use of the grinding wheel in the grinding process, the abrasive tool gradually loses its cutting ability due to wear caused by contact with the workpiece. When the grinding wheel reaches this condition, it becomes necessary to interrupt the process in order to restore its topography. The main method for preparing the grinding wheel is known as dressing [2,3]. This operation employs a tool called a dresser to remove worn abrasive grains and chips from its surface, thereby restoring its aggressiveness [4]. Performing the dressing operation with a single-point dresser is the simplest technique and is generally the most effective for producing a suitable cutting surface on a conventional grinding wheel and ensuring its efficient performance in the grinding process [4,5].

The dressing operation is essential for correcting flaws on the cutting surface of the grinding wheel, thereby ensuring the surface quality of the ground parts [6]. For this reason, researchers in the field adopt the slogan: “grinding is dressing” [6,7]. Monitoring the sharpness condition of the grinding wheel during the dressing operation is a relevant scientific topic for the optimization of the grinding process and the reduction in manufacturing costs.

Since 1984, acoustic emission (AE) sensors have been used for the indirect monitoring of conventional grinding wheels, both during the grinding process (to prevent damage to the workpiece) and throughout the dressing operation, with the objective of ensuring that the grinding wheel is in suitable condition for use [8,9]. The main advantage of this sensor is its ability to capture high-frequency signals, higher than the frequencies generated by the machines and the surrounding environment [10]. However, its implementation cost is relatively high, which represents a limiting factor for its application [11]. Thus, the investigation of low-cost devices has become a growing topic in recent years, with the aim of providing more affordable alternatives for the implementation of indirect monitoring of dressing and grinding in the industry.

The PZT transducer, known as a piezoelectric diaphragm or piezoelectric buzzer, is one of the devices tested in recent research for this purpose. Dotto et al. [12] used the signals captured by the diaphragm to construct acoustic maps for detecting flaws on the grinding wheel surface. The authors confirmed that the results obtained with this transducer were as effective as those obtained with an AE sensor.

More recently, Lopes et al. [13], introduced a new technique based on time-frequency analysis and the Ratio of Power statistic applied to signals captured by a PZT diaphragm. The authors proposed a new statistical parameter called the Wheel Shape Factor (WSF). The results showed that this approach is effective for quantifying the topographical regularity of the cutting surface of conventional aluminum oxide grinding wheels during the dressing operation, ensuring that the wheel is suitable for use in grinding. Although it is a comprehensive study, the authors did not explore all the possibilities of feature extraction through time-frequency analysis.

In this context, this study also employs time-frequency analysis to develop a new methodology based on the coefficients of variation in the parameters of the Short-Time Fourier Transform (STFT), with the objective of identifying the frequencies most associated with the condition of the grinding wheel. Unlike the work of Lopes et al. [13], this research aims to deepen the understanding of the interrelationship of the characteristic frequencies of the dressing operation, providing a more detailed analysis of the process.

2. Materials and Methods

The dressing tests were carried out on a tangential surface grinding machine, model RAPH 1055 from Sulmecânica (Porto Alegre, RS, Brazil), equipped with a NORTON (Guarulhos, SP, Brazil) aluminum oxide grinding wheel, model 38A.150.LVH, with dimensions of 324 mm × 25.4 mm × 127 mm, and a single-point diamond dresser manufactured using the Chemical Vapor Deposition (CVD) technique. Figure 1 shows the schematic diagram of the test bench used.

During the dressing operation, the acoustic waves generated by the contact between the dresser and the grinding wheels were captured by a low-cost piezoelectric diaphragm (PZT), model 7BB-35-3, manufactured by Murata Electronics (Kyoto, Japan), which was attached to the dresser support. This sensor converted the acoustic waves into electrical signals (I—PZT sensor signal), which were collected at a sampling frequency of 2 MHz using an oscilloscope, model DL850 (Tokyo, Japan), from Yokogawa (II—signal acquisition). Finally, the collected signals were sent to the computer for subsequent digital signal processing (III—stored signal). Index (a) in Figure 1 represents a real image of the PZT transducer used.

2.1. Dressing Tests

Before the definitive test, preliminary grinding and dressing trials were carried out in order to determine the most suitable parameters for the execution of the final test. The dressing parameters used in the definitive test are shown in

Table 1. Dressing parameters.

${\mathit{N}}_{\mathit{s}} \left[\mathbf{R}\mathbf{P}\mathbf{M}\right]$	${\mathit{d}}_{\mathit{s}}$ [mm]	${\mathit{V}}_{\mathit{s}}$ [m/s]	${\mathit{a}}_{\mathit{d}}$ [mm]	${\mathit{b}}_{\mathit{d}}$ [µm]	${\mathit{t}}_{\mathit{d}}$ [s]	${\mathit{S}}_{\mathit{d}}$ [mm]	${\mathit{U}}_{\mathit{d}}$	${\mathit{P}}_{\mathit{d}}$
1800	319.84	30.14	0.01	800	5.820	0.1455	5.5	30

, where $D_s$ is the grinding wheel diameter; $U_d$ is the overlap ratio; $V_s$ is the grinding wheel peripheral speed or cutting speed; $a_d$ is the dressing depth; $b_d$ is the dresser width of action; $n_s$ is the grinding wheel rotational speed; $t_d$ is the dressing time; and finally, $S_d$ is the axial feed of the dresser per wheel revolution, also referred to as the dressing feed.

The dresser width of action was determined using a DTN digital microscope, model USB: DNT DigiMicro 2.0 Scale (Dietzenbach, Germany). This equipment, equipped with a 2-megapixel camera, enabled precise measurement of the diamond tip. The microscope software was calibrated using the 10 mm diameter of the dresser body itself as a dimensional reference. After calibration, images of the diamond tip were captured and magnified for measurement. All images were acquired from the same position, approximately 8 mm from the tool tip. The width of action was then measured based on a dressing depth of 0.01 mm (10 µm).

The method used for carrying out the definitive test is divided into two main stages: (i) To introduce flaws on the cutting surface of the grinding wheel, a severe grinding process was applied to ABNT 1020 steel workpieces with dimensions of 150 mm × 48 mm × 12 mm. The machining consisted of 20 passes of the grinding wheel over the workpiece without the use of cutting fluid, applying a cutting depth of 20 µm and a table speed of approximately 48 mm/s. (ii) After the flaws were introduced on the grinding wheel surface, the dressing test was initiated, this time using cutting fluid.

2.2. Digital Signal Processing

The digital processing of the AE signals was performed using MATLAB^® version R2025b. Initially, only the data related to the dressing pass were extracted from the original signals of the PZT diaphragm. This was necessary because all collected signals consisted of noise before the dressing pass, the signal corresponding to the dressing pass, and noise after the dressing pass.

After separating the signals, the STFT coefficients were calculated using the spectrogram algorithm available in MATLAB^®. To define the window length used in the STFT of the signals, a specific algorithm was developed, thus avoiding the need to determine this parameter through trial and error.

After performing preliminary analyses and processing, it was possible to define the parameters of the Short-Time Fourier Transform (STFT), including the most appropriate window type for calculating its coefficients. In this process, several windows were tested, including Hamming, Hanning, Blackman, Flattop, Bartlett, Kaiser, and Tukey. Based on the analyses carried out, the Kaiser window was selected as the most appropriate, as it provided better attenuation of background noise and lower distortion of frequency amplitudes in the range of 20 to 600 kHz.

With the parameters defined, the STFT coefficients were calculated for each AE signal using the adjustments presented in

Table 2. Short-Time Fourier Transform (STFT) parameters.

Short-Time Fourier Transform (STFT)
Window Type	Kaiser
Window Length	4096 points
Overlay	75%
DFT	8192 points
Effective interval between windows	0.512 ms

.

Next, for each STFT curve over time, the coefficient of variation (CV) was obtained by dividing the standard deviation by its mean value. This resulted in a CV curve as a function of frequency. To attenuate the high-frequency components present in the CV curves, a moving average filter with a 32-point sliding window was applied. Finally, the visualization of the coefficient of variation in the STFT as a function of the number of dressing passes and frequency was performed using a three-dimensional map.

3. Results and Discussion

3.1. Original PZT Signal

The signals captured during the dressing operation of the conventional grinding wheel by the PZT diaphragm, corresponding to the 2nd and 30th passes, are shown in Figure 2. It can be observed that the 2nd pass (red line) presents irregular amplitudes over time, indicating that at this initial stage of dressing, the cutting surface of the grinding wheel exhibits irregularities caused during grinding. This results in reduced contact with the dresser and consequently produces a low level of acoustic excitement. This behavior is characteristic of a worn grinding wheel. In other regions of the 2nd pass over time, high amplitude values can be observed, attributed to the large amount of chips embedded on the grinding wheel surface. At these points, the dresser has greater contact with the accumulated material, thereby generating a more intense acoustic signal.

On the other hand, in the 30th pass (blue line), an increase in signal amplitude can be observed, evidencing a higher intensity of the acoustic waves generated by the contact between the dresser and the new abrasive grains of the grinding wheel. Furthermore, a lower variation in signal amplitude over time can be noticed, which suggests that as dressing progresses, the topography of the grinding wheel surface becomes more uniform, generating more consistent acoustic patterns over time.

3.2. Coefficient of Variation in the STFT

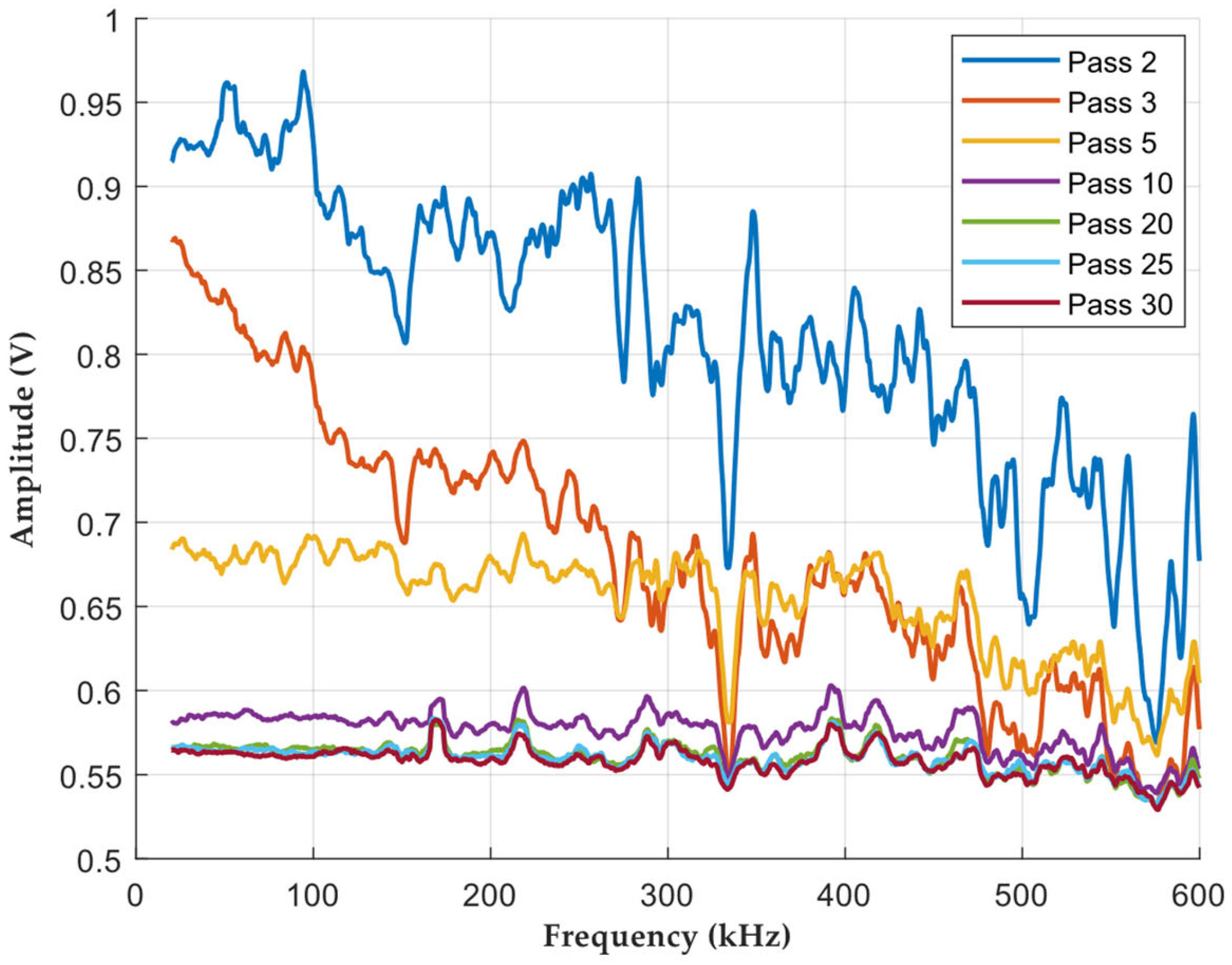
Figure 3 presents the coefficient of variation in the STFT over frequency for the 2nd, 3rd, 5th, 10th, 20th, 25th, and 30th dressing passes of the grinding wheel. Each curve represents a distinct stage of the dressing process, ranging from the 2nd pass (blue line) to the 30th pass (red line), allowing for a comparative analysis of the process evolution. It can be observed that the 2nd pass exhibits the highest coefficients of variation, especially in the range of 50 to 300 kHz. This behavior indicates greater signal instability, possibly due to the initial condition of the grinding wheel cutting surface, which still contains flaws, worn abrasive grains, and adhered chips. As the dressing progresses, this variation gradually decreases, suggesting a more homogeneous and regular surface after dressing.

In the 3rd pass, and even more notably in the 5th pass, a reduction in variation can be observed, mainly in the mid- and high-frequency ranges (>100 kHz). From the 10th pass onward, the coefficient of variation remains at low and relatively constant levels, suggesting that the dressing has already reached an equilibrium condition in the structure of the grinding wheel surface. In the 20th, 25th, and 30th passes, stabilization is evident, presenting the lowest coefficient of variation values, which indicates that the grinding wheel already has a well-defined and regular cutting surface.

Surface Matrix Visualization

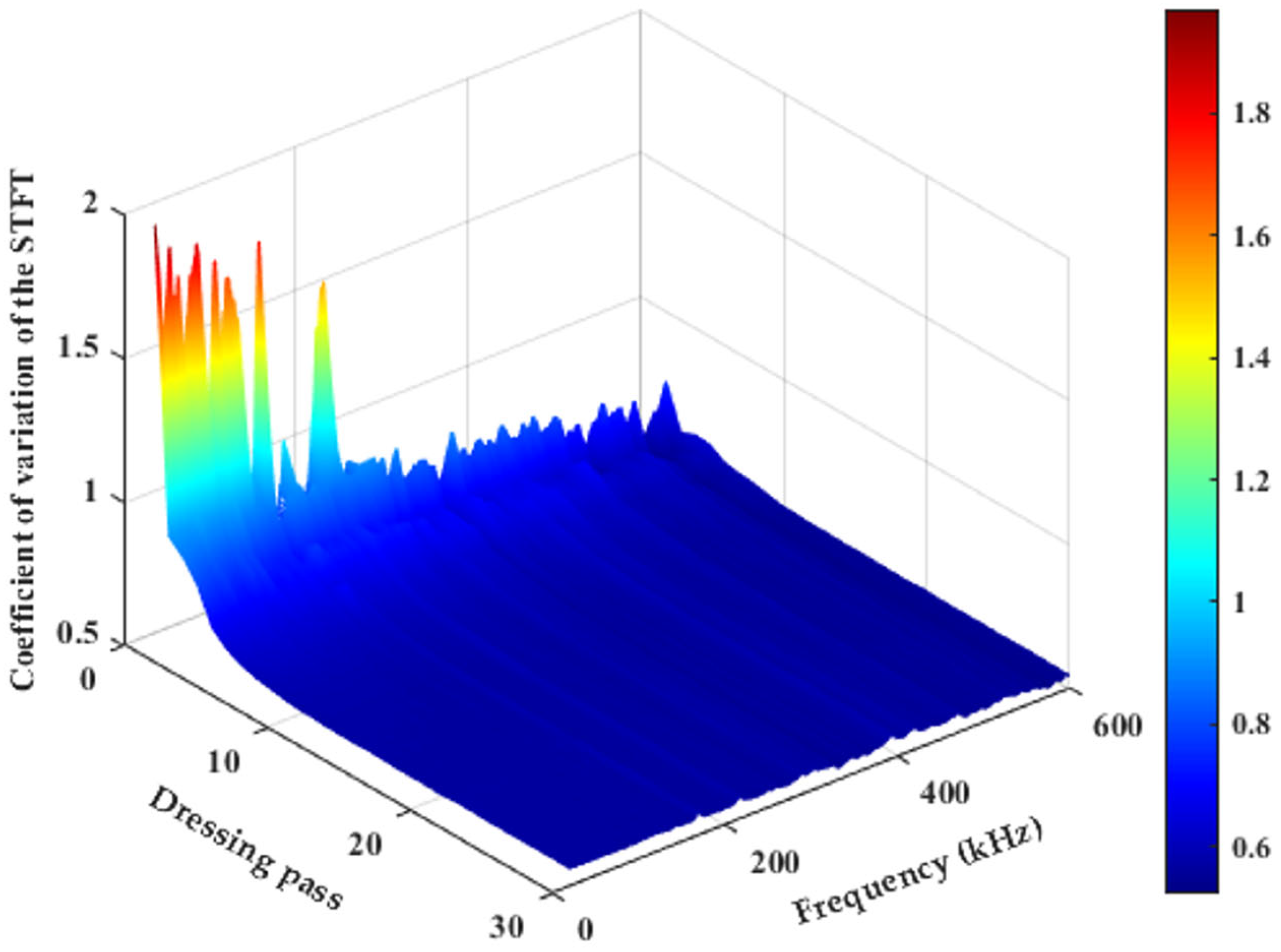
Figure 4 presents the evolution of the dressing operation as a function of the dressing passes and frequency, in the range of 20 to 600 kHz. It can be observed that the spectral region that best evidenced the transition from a non-dressed grinding wheel (high amplitudes of the STFT coefficient of variation) to a dressed grinding wheel (more stable amplitudes) was between 20 and 211 kHz, except for the intervals from 118 to 135 kHz and from 140 to 211 kHz. Therefore, the range of 20 to 100 kHz was identified as the most suitable for monitoring the dressing operation using the method proposed in this study.

Furthermore, it is noted that the stability of the STFT coefficient of variation is reached after approximately 10 to 15 passes, suggesting that this interval may represent a critical limit for the regularization of the grinding wheel surface. In other words, after 15 dressing passes, the cutting surface of the grinding wheel can be considered uniform and suitable for grinding.

Thus, the STFT coefficient of variation can serve as an objective indicator to support the operator in decision-making, ensuring that the dressing is interrupted at the optimal moment. In this way, the proposed methodology reduces the risks of incomplete dressing, which would impair grinding quality, while minimizing operational costs by preventing unnecessary wear of the abrasive material and increasing process efficiency.

4. Conclusions

The present study demonstrated that the spectral variation in the STFT coefficient of variation, extracted from signals acquired by a low-cost PZT diaphragm during the dressing operation, can serve as a reliable and objective indicator for assessing the regularization of the grinding wheel surface. The results revealed that the signals exhibited pronounced instability in the initial passes, followed by a progressive stabilization between the 10th and 15th passes. This behavior confirms that the dressing process effectively restored the cutting surface, rendering the wheel suitable for subsequent grinding operations.

Three-dimensional map further validated this stabilization trend, reinforcing the potential of the coefficient of variation as a decision-support tool for operators in determining the optimal point to interrupt dressing. Additionally, the frequency band between 20 kHz and 100 kHz proved to be the most sensitive for feature extraction, as it enabled a clear distinction between irregular and regularized cutting surfaces. This range was identified as the most representative for monitoring the process with precision and robustness.

The proposed methodology contributes significantly to the optimization of dressing operations by ensuring improved grinding quality, reduced dresser wear, and lower abrasive consumption. These advantages highlight the potential of the approach for increasing process efficiency and sustainability.

For future research, it is recommended to extend the methodology to different dressing conditions, wheel geometries, and sensor types. Furthermore, integration with intelligent systems—such as artificial neural networks and fuzzy algorithms—could enable automatic classification of grinding tool conditions, enhancing the level of autonomy and reliability in industrial applications. The conclusions presented here remain valid within the specific experimental conditions employed, including the selected transducer, grinding wheel, and single-point dresser.