Bilateral Teleoperation with Force Feedback and Obstacle Detection-Based Navigation for Mobile Robots in Congested Environments ^†

Abstract

This paper presents the implementation of a bilateral teleoperation system for mobile robots operating in congested environments, incorporating force feedback and obstacle-aware navigation. The system uses the Novint Falcon device as the master interface and a mobile robot as the slave unit. A control strategy is developed that integrates mechanical impedance models and a force-based obstacle detection and avoidance algorithm. Additionally, the control law incorporates feedback based on the relative velocities of surrounding objects to account for dynamic interactions and contribute to system stability. Experimental tests were conducted to evaluate the performance of the teleoperation system, focusing on remote navigation, obstacle avoidance, and bidirectional interaction through force feedback in congested scenarios.

1. Introduction

Bilateral teleoperation is currently one of the most prominent applications in the field of technological innovation and robotics [1]. This technology enables direct interaction between a human and a robot within a virtual or remote environment. In recent years, considerable advances have been made in the remote control of robots and autonomous vehicles [2]. In particular, bilateral teleoperation with haptic feedback enhances the operator’s perception and improves task performance [3]. This technology has found applications in numerous fields, such as medicine, where teleoperated surgical systems integrate haptic feedback to increase precision and safety [4], as well as in space and underwater exploration, allowing for safe manipulation in otherwise inaccessible environments [5], and in hazardous or radioactive facilities, where it ensures operator safety by maintaining physical separation [1].

To address the challenge of achieving safe and reliable remote control of mobile robots, various strategies have been proposed, such as the integration of repulsive haptic feedback [6,7] and shared control approaches that facilitate collaboration between the robot and the operator [8]. Additionally, obstacle avoidance algorithms have been developed to ensure safe navigation, enabling the robot to decelerate or change its trajectory prior to potential collisions [9]. Several advanced control strategies have also been designed to ensure stability and robustness in bilateral teleoperation. Among these, Lyapunov-based controllers offer reliable trajectory tracking in systems with uncertain dynamics [10], while sliding mode control (SMC) enhances robustness against model uncertainties and external disturbances, particularly when used in hybrid schemes incorporating null-space projection and sliding surfaces [11]. Moreover, adaptive controllers enable online tuning of control parameters to cope with changes in the environment [12].

The main contributions of this work are summarized as follows. A bilateral teleoperation architecture is proposed for the TurtleBot3 Burger mobile robot, incorporating force feedback into the Novint Falcon haptic interface. The system estimates relative velocity to enhance the operator’s interactive experience. A mechanical impedance model is implemented to enable smooth and bidirectional interaction between the human operator and the robot. In addition, an obstacle avoidance algorithm based on virtual force fields is integrated, allowing the robot to adjust its velocity profile upon detecting obstacles, prioritizing safe navigation over strict reference tracking. It is worth noting that the trajectory-tracking and obstacle-avoidance controllers operate without switching, thereby preserving system stability by avoiding controller commutation, whereas in [9,10,11], controller switching is employed. The robot does not stop to replant, and the human–robot interaction is enhanced through impedance control, which is not considered in [8]. Furthermore, a velocity control strategy with improved feedback is applied to maintain system stability in congested environments with static obstacles. Finally, the proposed system is experimentally validated, which is not addressed in [7], demonstrating its capability to perform remote operation, obstacle detection, and force-reflective interaction in cluttered scenarios.

The article is organized as follows: Section 2 introduces the TurtleBot3 Burger platform, the robot velocity filtering approach, and the implemented mechanical impedance model. Section 3 presents the obstacle avoidance algorithm and the mathematical formulation of the Lyapunov-based controller. Section 4 describes the experimental test conducted to evaluate the performance of the robot and the overall bilateral teleoperation system. Finally, Section 5 provides the conclusions of this work.

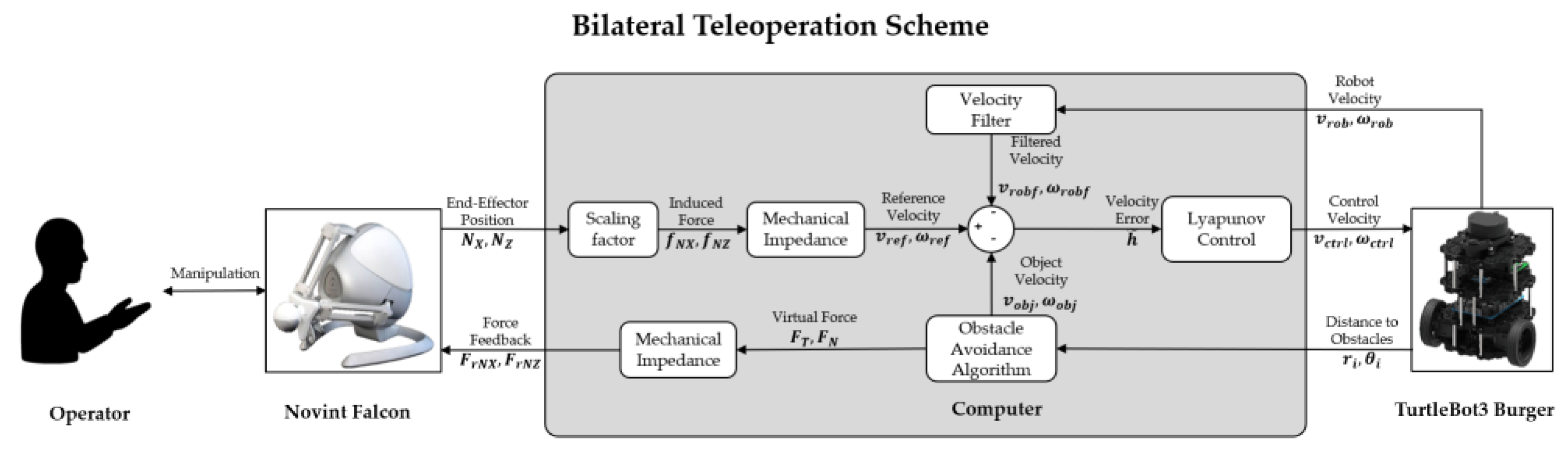
2. Modeling

2.1. TurtleBot3 Mobile Robot

This work utilizes the TurtleBot3 Burger, manufactured by Robotis Co., Ltd., Daejeon, South Korea as the slave platform for bilateral teleoperation. Designed for ROS-based development, the robot features wheel encoders for velocity estimation and a 360° LiDAR sensor for precise obstacle detection. Control signals are limited to ±0.2 m/s for linear velocity and ±1 rad/s for angular velocity. Communication with the MATLAB-Simulink environment is established via the ROS middleware, allowing for real-time data exchange and implementation of the proposed control architecture.

2.2. Velocity Filter

To mitigate the effects of noise, sharp spikes, and outliers present in the velocity measurements of the TurtleBot3 Burger robot, a three-stage filtering process was implemented. This process consists of outlier removal, a moving median filter [3], and an exponential moving average (EMA) filter. The goal is to obtain cleaner and smoother estimates of the robot’s linear and angular velocities, providing a more accurate representation of its dynamic behavior.

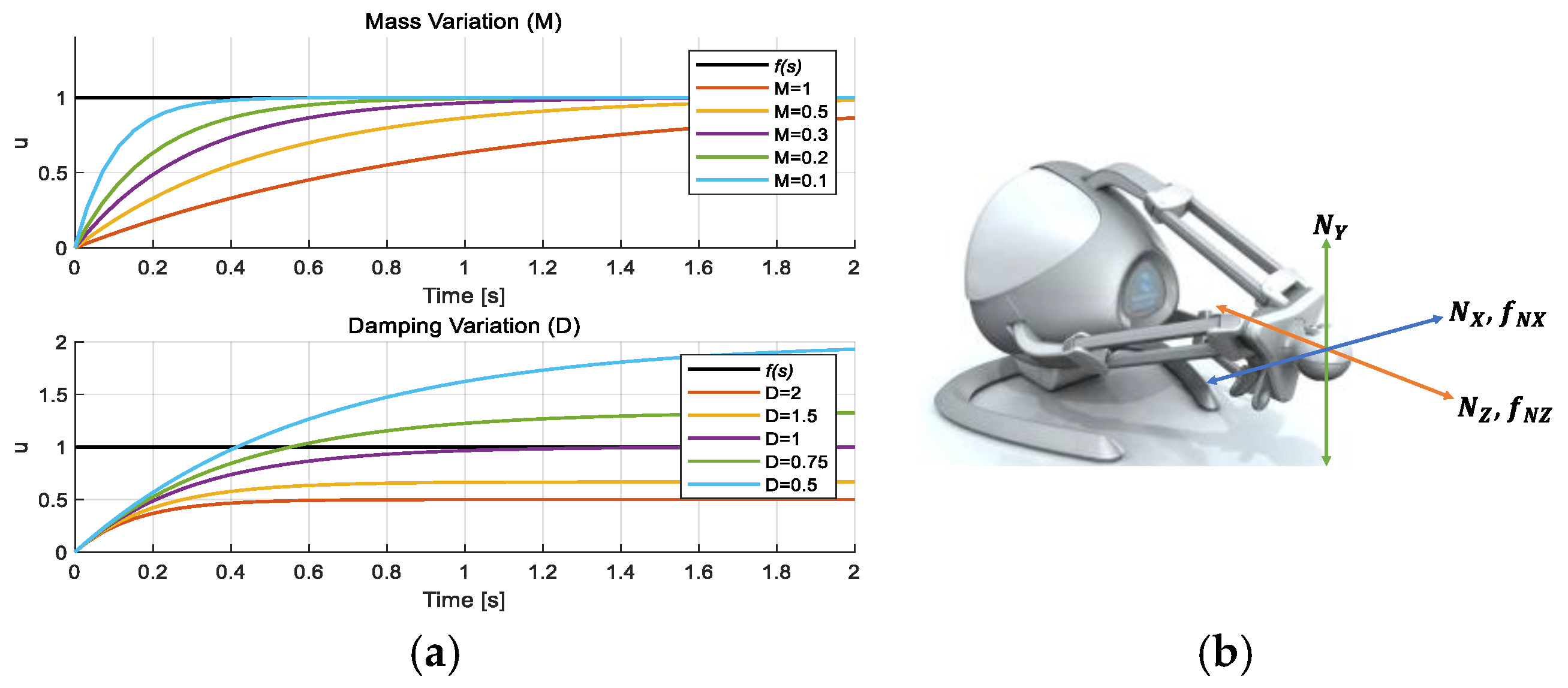
2.3. Mechanical Impedance

Mechanical impedance is applied in two key components of the system: first, in the interaction force exerted by the operator on the Novint Falcon device is manufactured by Novint Technologies, Inc., Albuquerque, NM, USA, which is used to generate the reference velocities fed into the Lyapunov-based controller; and second, in the virtual force fields used to compute the feedback forces transmitted to the Novint Falcon. The mechanical impedance is defined by:

$$v\left(s\right)={\displaystyle \frac{1}{Ms+D}} f(s)$$

(1)

where $f\left(s\right)$ is the induced force, $v\left(s\right)$ is the induced velocity, $M$ represents the mass, and $D$ denotes the damping of the system. Figure 1a illustrates the variation of the impedance parameters.

2.3.1. Reference Velocity

The mechanical impedance model is employed to generate the reference velocities, enhancing the operator’s immersive experience during the bilateral teleoperation of the TurtleBot3 Burger robot, while simultaneously attenuating abrupt changes in the command signals. The model uses the parameters $D=1$, to ensure unit gain of the impedance model, and $M=0.3$, experimentally selected to provide smooth force feedback and guarantee a fast response, without requiring readjustment for different operating conditions. This results in the following applied impedance model:

$$\left[\begin{array}{c}{\nu }_{ref}\\ {\omega }_{ref}\end{array}\right]= \left[\begin{array}{cc}\frac{1}{0.3s+1}& 0\\ 0& \frac{1}{0.3s+1}\end{array}\right]\left[\begin{array}{c}{f}_{NZ}\\ f_{NX}\end{array}\right]$$

(2)

Here, ${\nu }_{ref}$ and ${\omega }_{ref}$ denote the linear and angular velocities, respectively, while $f_{NZ}$ and $f_{NX}$ represent the operator-induced forces. These forces are derived from the end-effector positions $N_Z$ and $N_X$ of the Novint Falcon device, scaled appropriately, and aligned with the directions illustrated in Figure 1b.

2.3.2. Feedback Force

To provide smooth and continuous force feedback to the Novint Falcon device, a mechanical impedance model is implemented. This approach allows the operator to perceive the interaction forces between the robot and its environment in a gradual manner, avoiding abrupt transitions that could compromise system stability or degrade the teleoperation experience. The model uses parameters $D=1$, to guarantee the unity gain of impedance model, and $M=0.1,$ experimentally selected to provide smooth force feedback and guarantee a fast response, without requiring readjustment for different operating conditions. This results in the following relationship between the fictitious forces generated by obstacle detection and the feedback forces applied to the device:

$$\left[\begin{array}{c}{F}_{rNZ}\\ F_{rNX}\end{array}\right]=\left[\begin{array}{cc}\frac{1}{0.1s+1}& 0\\ 0& \frac{1}{0.1s+1}\end{array}\right]\left[\begin{array}{c}{F}_N\\ F_T\end{array}\right]$$

(3)

where $F_{rNZ}$ and $F_{rNX}$ denote the feedback force components applied to the Novint Falcon along the $Z$ and $X$ axes, respectively. The terms $F_N$ and $F_T$ correspond to the normal and tangential components of the artificial force field generated based on the proximity of obstacles detected by the robot’s LiDAR sensor.

3. Controllers

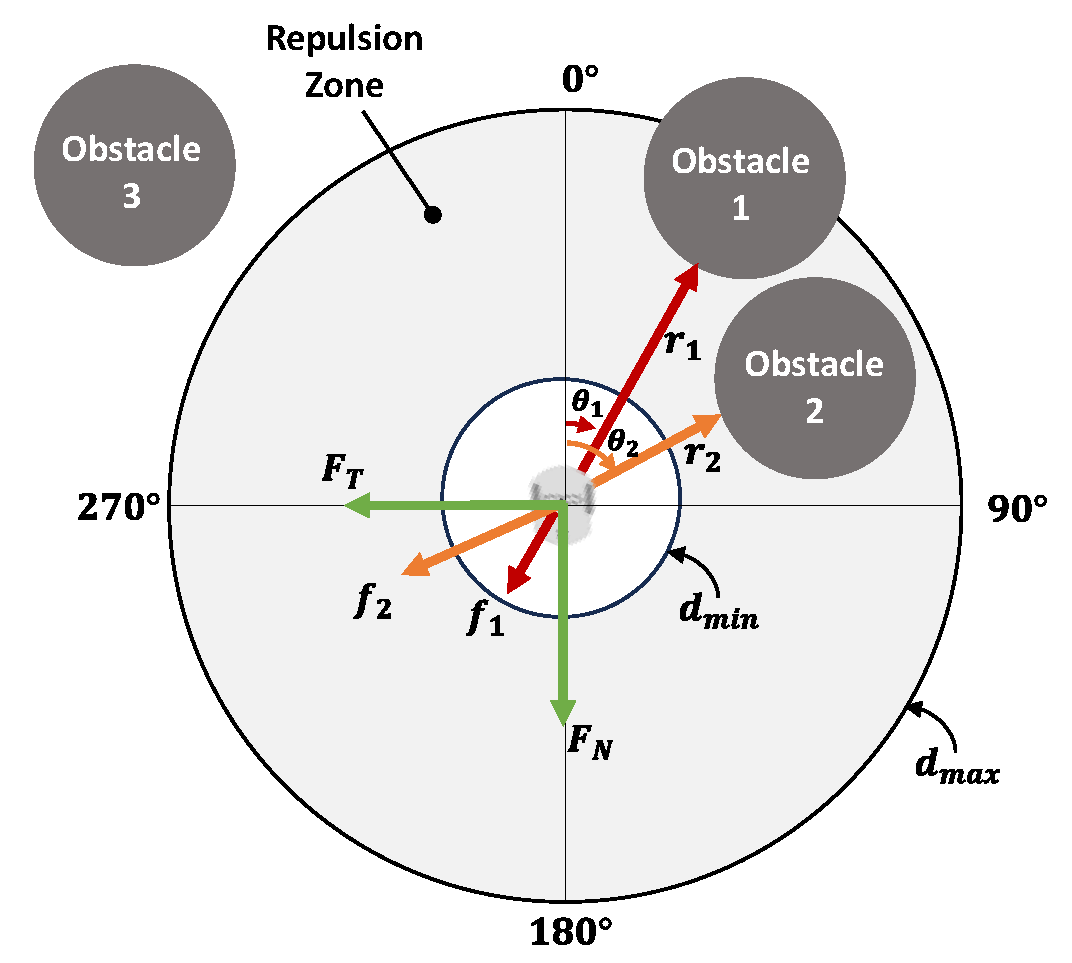
Figure 2 illustrates the complete architecture of the bilateral teleoperation system implemented in this study. It depicts the velocity control of the TurtleBot3 Burger robot carried out by the human operator through interaction with the Novint Falcon haptic device, as well as the force feedback provided to the device based on the obstacle avoidance algorithm.

3.1. Obstacle Avoidance Algorithm

The obstacle avoidance strategy is based on virtual force fields, where virtual repulsive forces are generated with magnitudes inversely proportional to the distance between the robot and nearby obstacles. In addition to these repulsive forces, a velocity component is introduced in opposition to the robot’s motion to prevent potential collisions.

3.1.1. Virtual Forces

The virtual forces act in the opposite direction to objects located within the repulsion zone, as illustrated in Figure 3. In this context, $d_{min}$ and $d_{max}$ define the minimum and maximum distances that determine the limits of the repulsion zone. The parameters $r_i$ and ${\theta }_i$ correspond to the radial distances and angles of incidence between the robot and obstacles, which are measured using the onboard 360° LiDAR sensor.

The magnitude of the virtual forces $f_i$ is determined through linear interpolation, expressed as:

$$f_i=f_{max}-{\displaystyle \frac{f_{max}}{d_{max}-d_{min}}}\left(r_i-d_{\mathrm{m}\mathrm{i}\mathrm{n}}\right)$$

(4)

where $f_{max}$ is the maximum feedback force supported by the Novint Falcon device, set to 10 N.

To provide force feedback to the operator, the virtual forces must be decomposed into tangential $F_T$ and normal $F_N$ components, which are computed as follows:

$$F_T=K_T {\sum }_{i=0}^{360}\left(f_i \sin \left({\theta }_i\right)\right)$$

(5)

$$F_N=K_N {\sum }_{i=0}^{360}\left(f_i \cos \left({\theta }_i\right)\right)$$

(6)

where $K_T$ and $K_N$ are coupling constants. The forces feedback to the Novint Falcon device are then obtained by applying the mechanical impedance model to these tangential and normal components of the virtual forces.

3.1.2. Object Velocity

The object velocities $v_{obj}$ and ${\omega }_{obj}$ represent the linear and angular velocity components, respectively, that act in opposition to the robot’s motion to prevent collisions with nearby obstacles [10]. These velocities are derived from the feedback forces applied to the Novint Falcon device using scaling factors, as shown in Equations (7) and (8):

$$v_{obj}=K_v F_{rNZ}$$

(7)

$${\omega }_{obj}=K_{\omega } \mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}\left(F_{rNX}\right)$$

(8)

where $K_v$ and $K_{\omega }$ are the scaling factors for the linear and angular object velocities, respectively. These coefficients ensure that the resulting object velocities remain within the same operational range as the reference velocities, thereby enabling a proper system response when obstacles are detected within the repulsive zone.

3.2. Lyapunov Control

The linear and angular velocity control of the TurtleBot3 Burger is achieved through a Lyapunov-based controller. System stability is analyzed by proposing a Lyapunov candidate function and evaluating its time derivative.

The control law is given in Equation (9), where the hyperbolic tangent function $tanh$ is incorporated to prevent signal saturation, enhance transient response, and mitigate undesirable oscillations:

$$\left[\begin{array}{c}{v}_{ctrl}\\ {\omega }_{ctrl}\end{array}\right]=\int \left(\left[\begin{array}{c}{\dot{v}}_{ref}\\ {\dot{\omega }}_{ref}\end{array}\right]+K \mathit{tanh}\left(\tilde{h}\right)\right)$$

(9)

Here, $v_{ctrl}$ and ${\omega }_{ctrl}$ represent the linear and angular control velocities, respectively, $v_{ref}$ and ${\omega }_{ref}$ are the reference linear and angular velocities, $K$ is a gain matrix, and $\tilde{h}$ is the velocity error vector defined in Equation (10). This formulation also includes the object velocities to ensure that the robot avoids obstacles in its environment, even when the operator applies a force opposite to the feedback force.

$$\tilde{h}=\left[\begin{array}{c}{v}_{ref}-v_{rob}-v_{obj}\\ {\omega }_{ref}-{\omega }_{rob}-{\omega }_{obj}\end{array}\right]$$

(10)

where $v_{rob}$ and ${\omega }_{rob}$ denote the linear and angular velocities of the robot, respectively. Assuming perfect velocity tracking in closed-loop control $v_{rob}=v_{ctrl}, {{\omega }_{rob}=\omega }_{ctrl}$, the time derivative of the velocity error becomes:

$$\dot{\tilde{h}}=\left[\begin{array}{c}{\dot{v}}_{ref}-{\dot{v}}_{ctrl}-{\dot{v}}_{obj}\\ {\dot{\omega }}_{ref}-{\dot{\omega }}_{ctrl}-{\dot{\omega }}_{obj}\end{array}\right]$$

(11)

The proposed Lyapunov candidate function is:

$$V={\displaystyle \frac{1}{2}} {\tilde{h}}^T\tilde{h}$$

(12)

Deriving:

$$\dot{V}={\tilde{h}}^T\dot{\tilde{h}}$$

(13)

Substituting Equations (9) and (11) into Equation (13) yields:

$$\dot{V}=-{\tilde{h}}^T K tanh\left(\tilde{h}\right)-{\tilde{h}}^T \left[\begin{array}{c}{\dot{v}}_{obj}\\ {\dot{\omega }}_{obj}\end{array}\right]$$

(14)

Analysis of Equation (14) shows that when the object velocities are zero (i.e., no nearby obstacles), the Lyapunov derivative is strictly negative, guaranteeing asymptotic stability $\tilde{h}\to 0$. However, in the presence of obstacles, when the object velocities are non-zero, the $\dot{V}$ cannot be guaranteed to be negative. Therefore, stability cannot be assured in this case, as the control strategy prioritizes collision avoidance over exact reference velocity tracking.

4. Experimental Tests and Results

4.1. Experimental Setup and Parameters

To ensure safe operation within the available track space and maintain controlled robot movement, the reference linear and angular velocities were set to $\pm 0.1 \mathrm{m}/\mathrm{s}$ and $\pm 0.5 \mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}$, respectively. Based on these operational limits, the scaling factors in Equations (7) and (8) were defined as $K_v=0.1$ and $K_{\omega }=0.5$, ensuring consistency between the virtual object velocities and the reference signals. The repulsion zone parameters were defined with $d_{max}=40 \mathrm{c}\mathrm{m}$ and $d_{min}=10 \mathrm{c}\mathrm{m}$. The tangential and normal coupling constants were empirically set to $K_T=K_N=36$, ensuring smooth virtual forces within the operational range of the haptic device $\pm 10 \mathrm{N}$. Additionally, the gain matrix used in the Lyapunov-based controller was tuned experimentally to enhance system performance. The selected matrix is $K=\left[1.4 0; 0 1.3\right].$

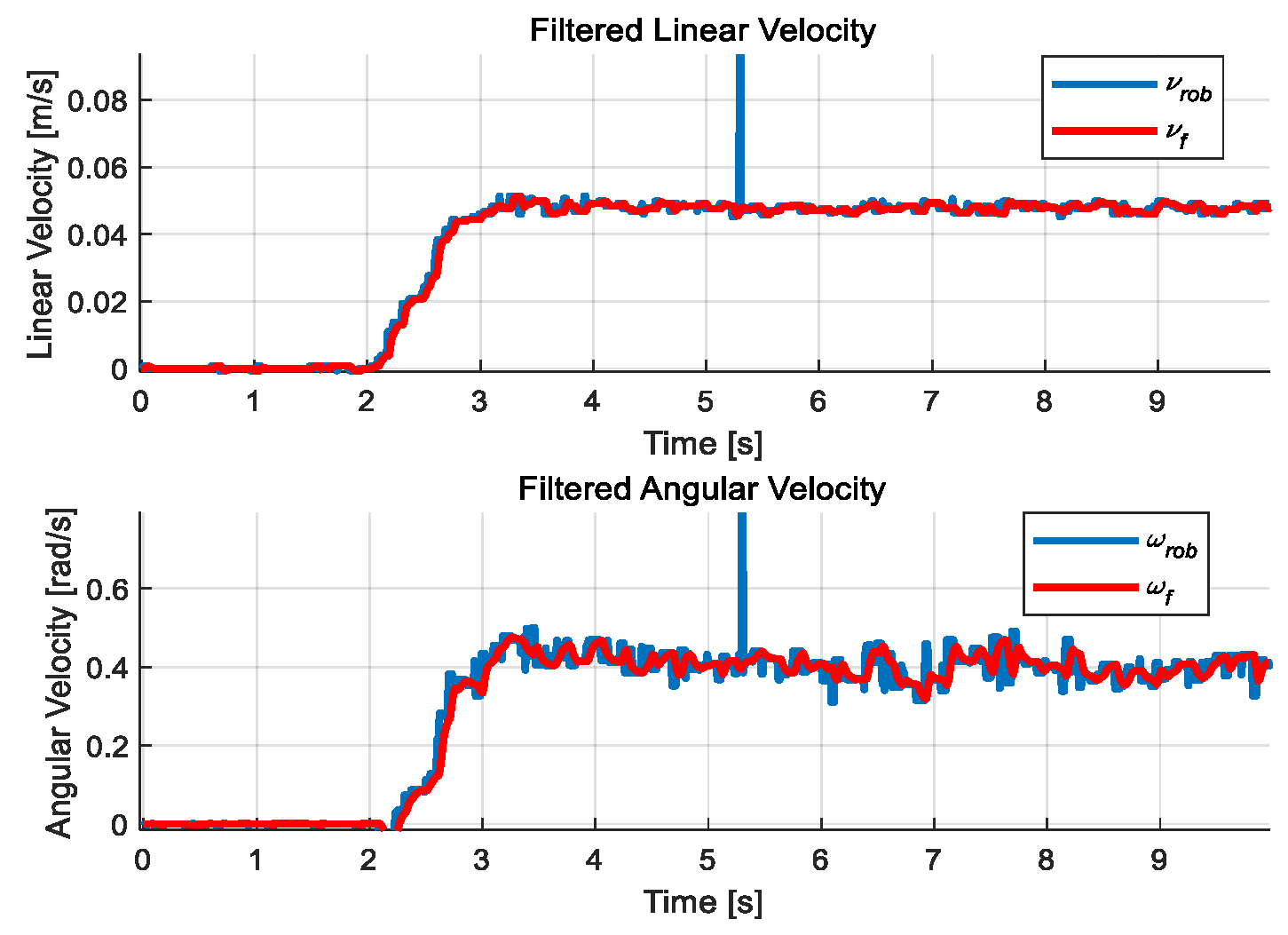
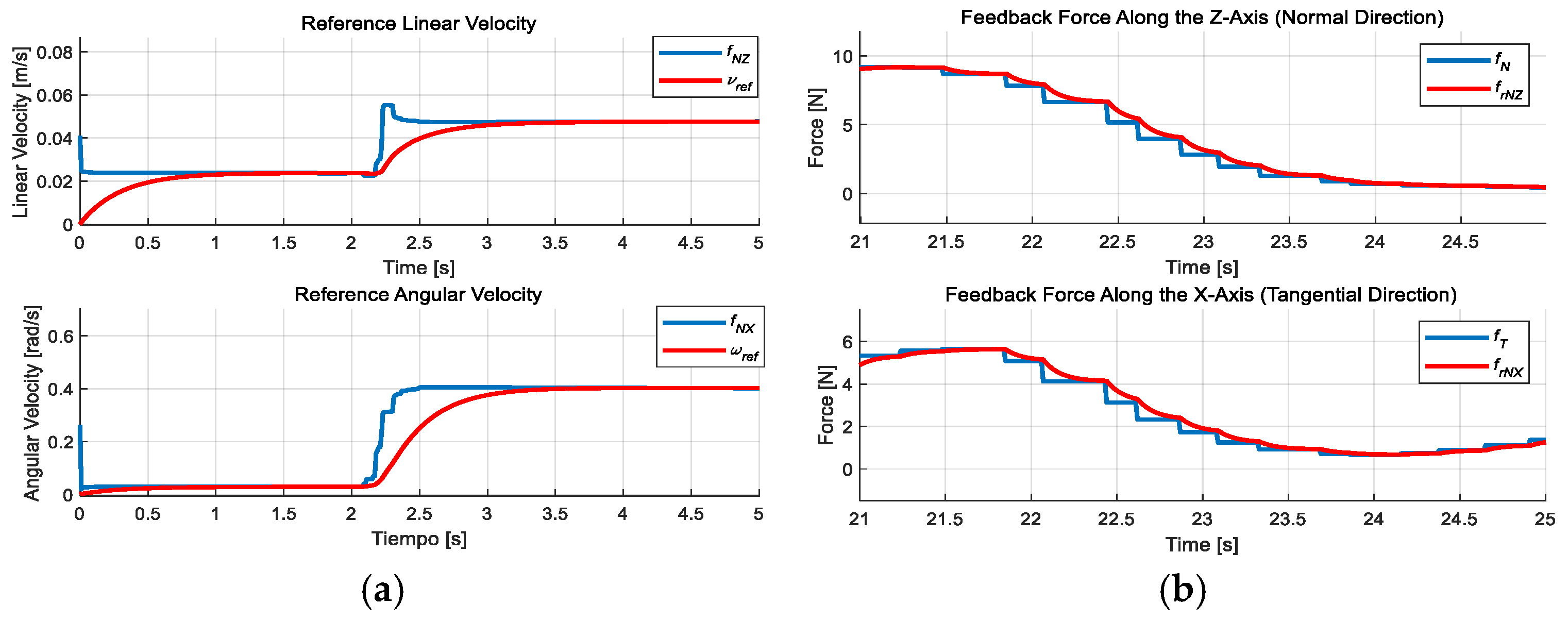
4.2. Test in an Obstacle-Free Environment

To evaluate the performance of each component of the bilateral teleoperation system, a test was conducted in an environment free of obstacles, where the robot navigated without external disturbances. Figure 4 shows the measured and filtered velocity signals of the robot. It can be observed that the implemented filtering stage effectively suppresses outliers, attenuates sharp peaks, and provides smoother and cleaner signals.

Figure 4 shows the measured and filtered velocity signals of the robot. The measured signal shows significant noise and an outlier around $t=5.2 \mathrm{s}$, which is due to the discrete nature of encoder-based odometry, producing erroneous velocity estimates at certain times. By contrast, the filtered signal is much cleaner and more accurately represents the robot’s true velocity, confirming the correct operation and necessity of the three-stage filter applied.

Figure 5a,b show the responses of the mechanical impedance model used to generate the reference velocities and the feedback forces applied to the Novint Falcon device, respectively. The application of impedance models results in smoother reference and feedback signals, thereby enhancing the human operator’s interaction with both the robot and its environment.

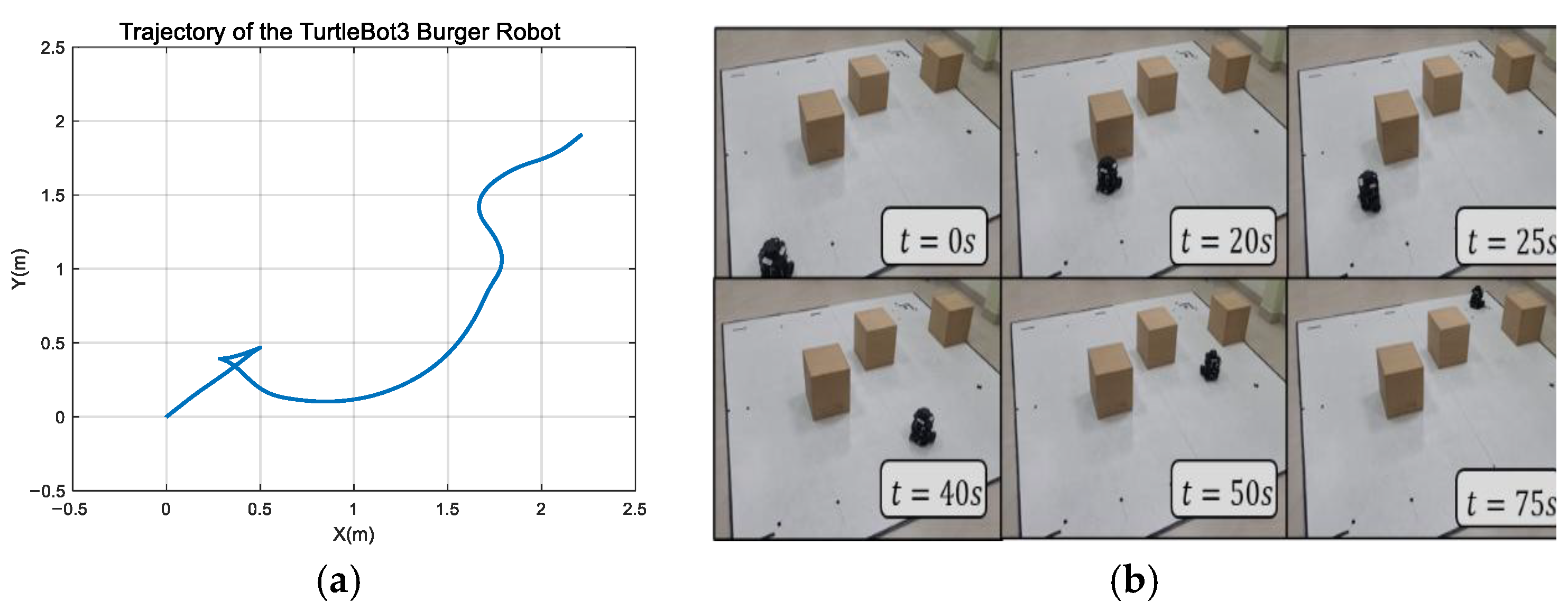
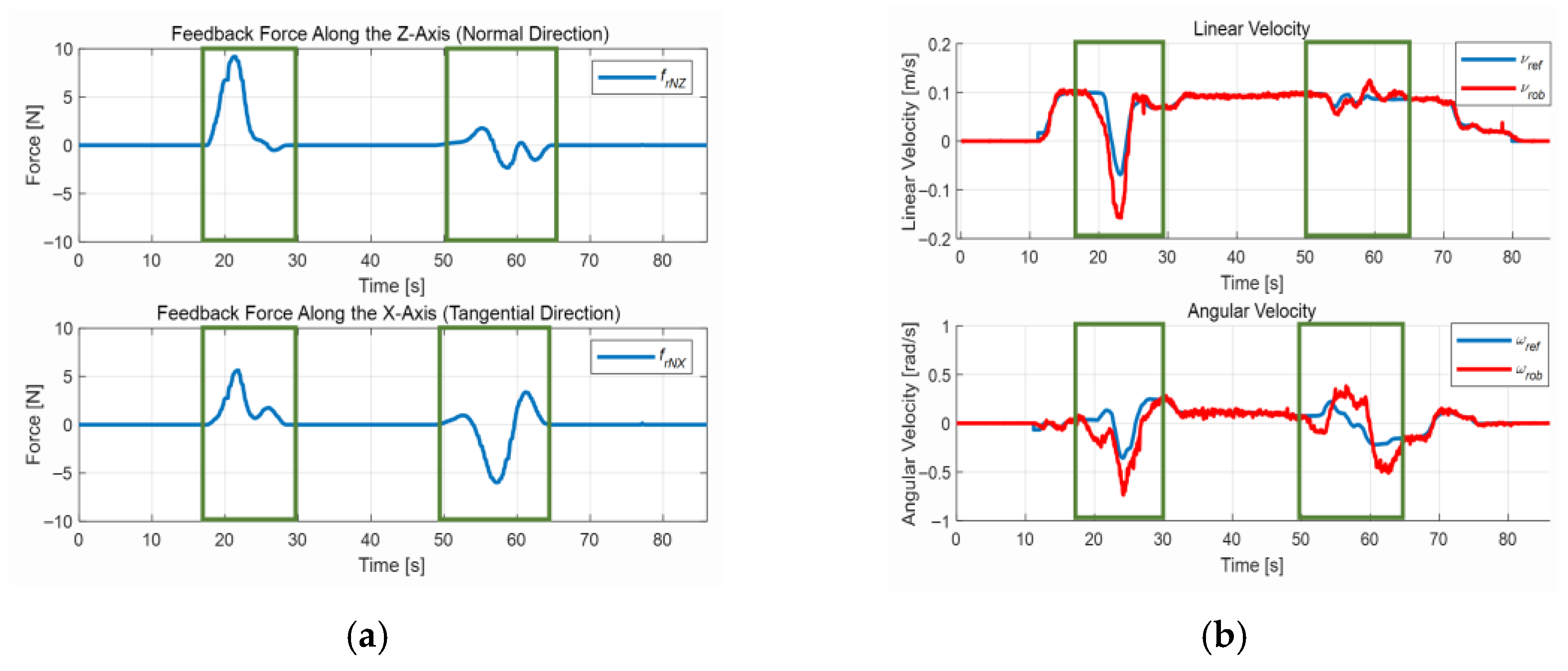
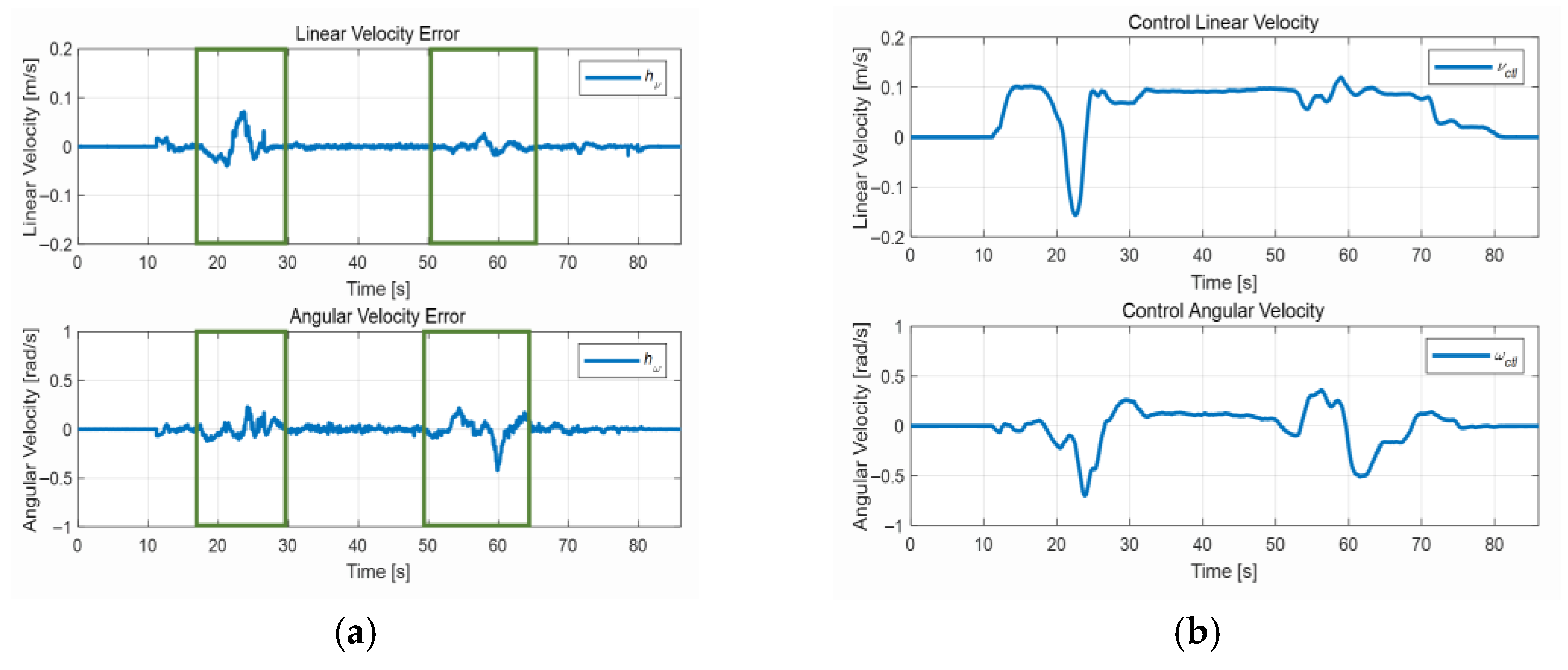
4.3. Test in a Congested Environment

To evaluate the full performance of the bilateral teleoperation system, an experimental test was conducted in an environment containing three obstacles distributed along the robot’s track. Figure 6a,b present both the trajectory of the mobile robot and a sequence of images that illustrate its movement during navigation through the environment.

Figure 7a shows the temporal evolution of the feedback forces applied to the Novint Falcon device during the test. Three intervals of interest were identified: from 0 to 16 s, from 30 to 50 s, and from 65 s onward, during which the feedback forces remain zero due to the absence of obstacles within the repulsion zone. Between 16 and 30 s, the robot’s diagonal approach to an obstacle generates feedback forces along both the Z and X axes of the device. Finally, during the interval from 50 to 65 s, the lateral approach to obstacles results in a greater feedback force along the X axis compared to the Z axis. Figure 7b presents the linear and angular velocity profiles, comparing the reference signals and the measured velocities of the robot during the experiment. During the intervals from 0 to 16 s, 30 to 50 s, and after 65 s, the robot’s velocities closely track the reference values, indicating the absence of obstacles within the repulsion zone. However, between 16 and 30 s, as the robot approaches an obstacle diagonally, variations occur in both linear and angular velocities due to the implemented control algorithm. Similarly, from 50 to 65 s, when the robot navigates laterally near obstacles, a notable adjustment is observed primarily in the angular velocity, reflecting the controller’s response to obstacle avoidance.

Figure 8a shows the velocity tracking errors, which remain minimal throughout the test except when an object enters the repulsion zone. In these instances, the errors increase as expected, reflecting the behavior defined by the obstacle avoidance algorithm. Figure 8b displays the control velocity commands sent to the robot. It is also observed that these commands remain within valid ranges, ensuring the proper operation of the robot.

5. Conclusions

The experimental tests conducted in a real environment demonstrated the effectiveness of the bilateral teleoperation system in enabling direct and precise interaction between the human operator and the TurtleBot3 Burger robot in congested scenarios. The implementation of mechanical impedance models smoothed the reference signals and haptic feedback, enhancing the operator’s experience by minimizing abrupt changes. Additionally, the obstacle avoidance algorithm based on virtual forces was experimentally validated, allowing the operator to clearly perceive the presence of obstacles and ensuring safe navigation. The Lyapunov controller exhibited satisfactory performance in velocity tracking when no obstacles were present and prioritized obstacle avoidance when obstacles entered the repulsion zone. These experimental results confirm the robustness and applicability of the system in real environments, highlighting the importance of future tests with moving objects and comparisons with alternative control schemes to further optimize performance.