Bilateral Teleoperation of a Formation of Mobile Robot Using Proportional Control and Obstacle Avoidance: Experimental Results †
Abstract
1. Introduction
2. Modeling
2.1. Kinematic Model of the Mobile Robots
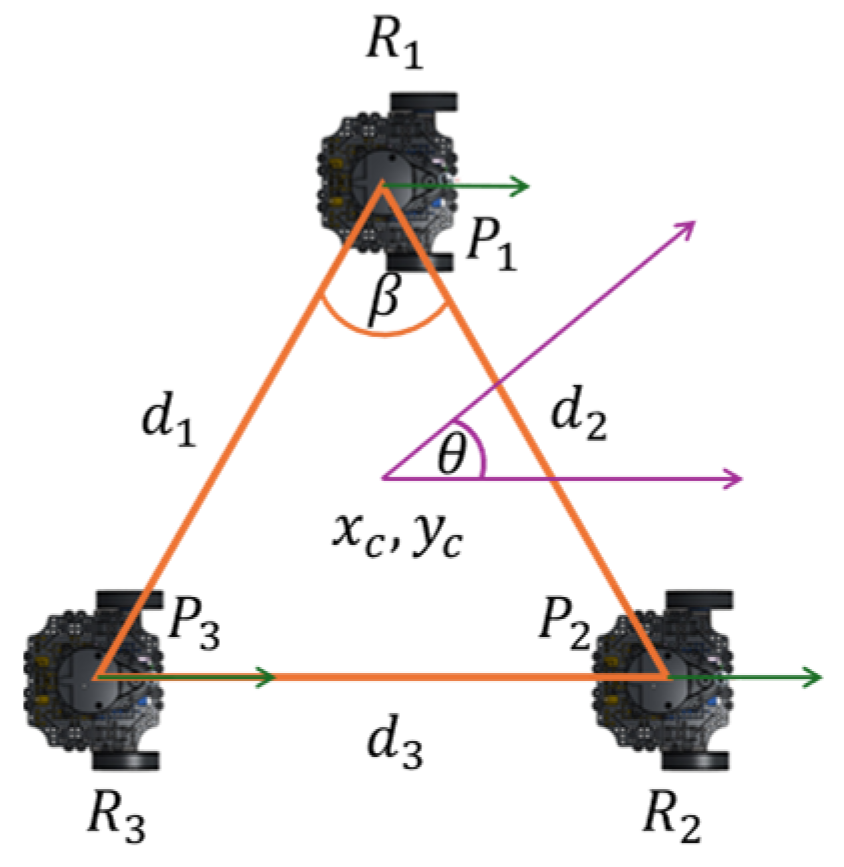
2.2. Desing of the Formation Model
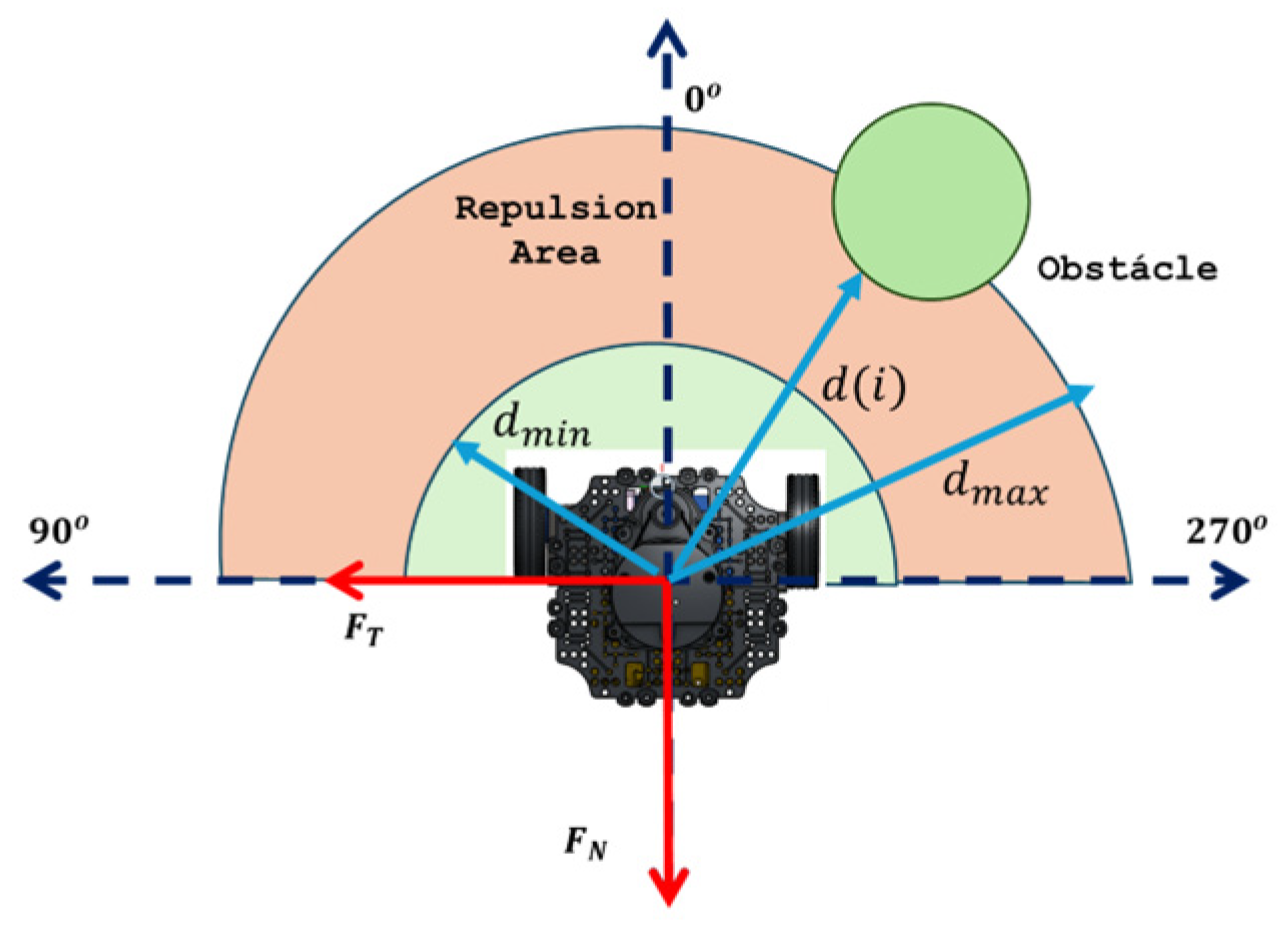
2.3. Obstacle Avoidance Model
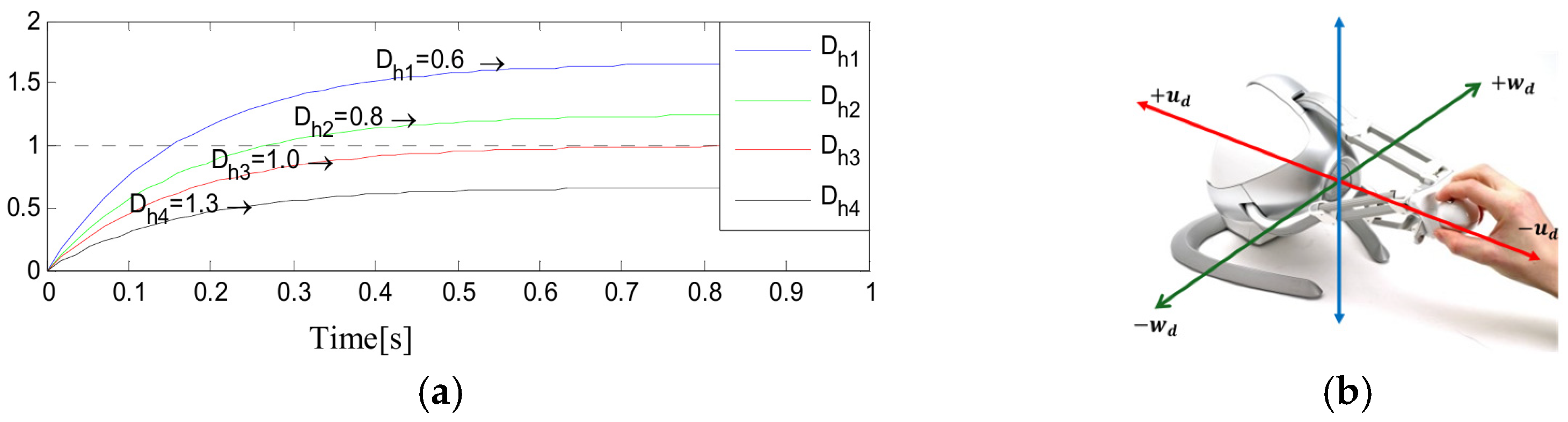
2.4. Modeling of the Induced Velocity
3. Controllers
3.1. Reference
3.2. Proportional-Type Formation Controller Design
3.3. Obstacle Avoidance Controller Design
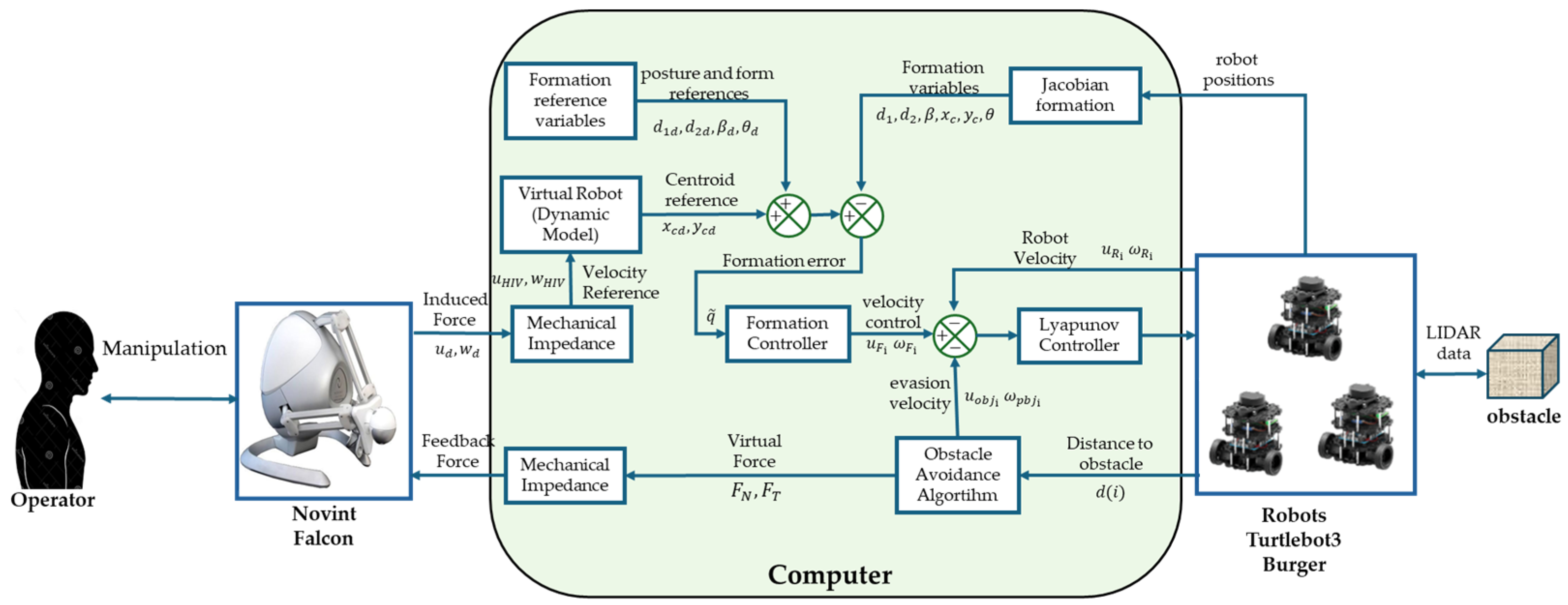
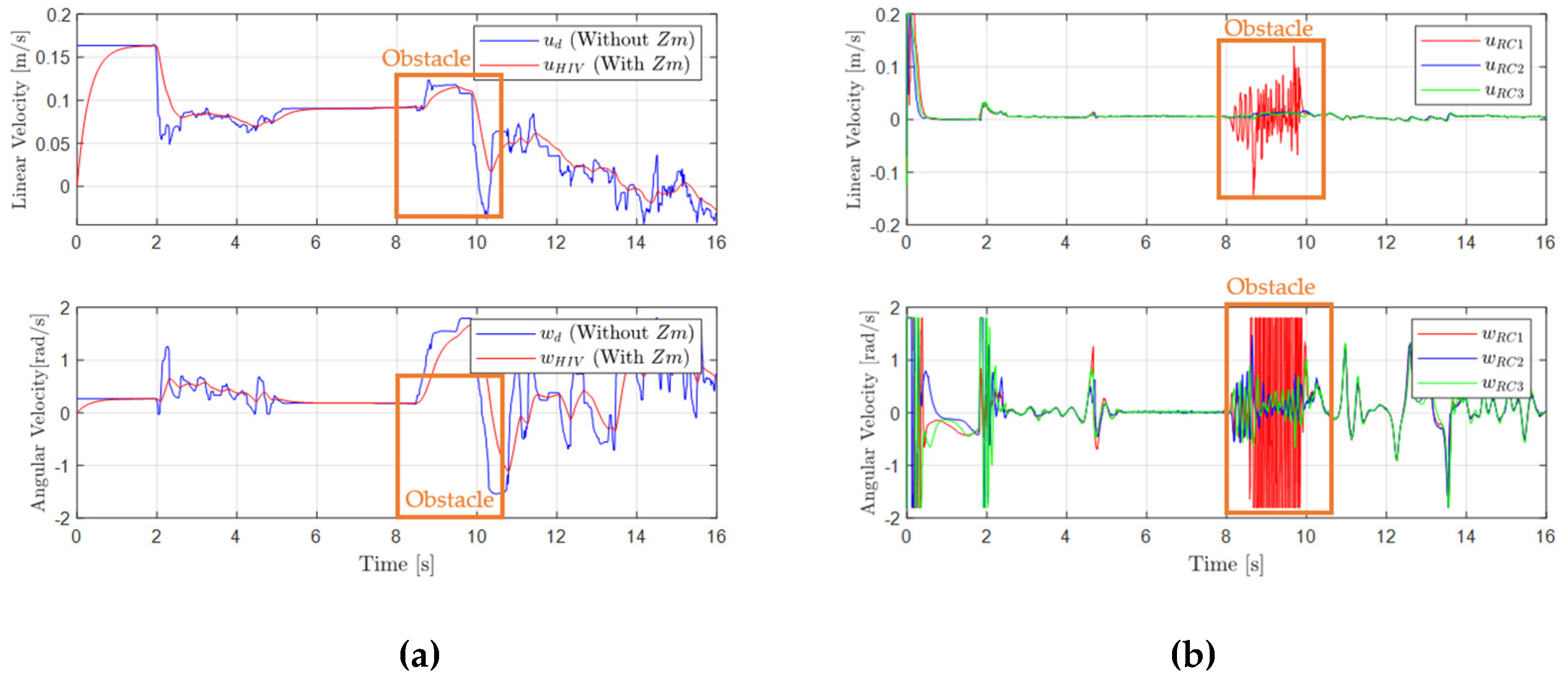
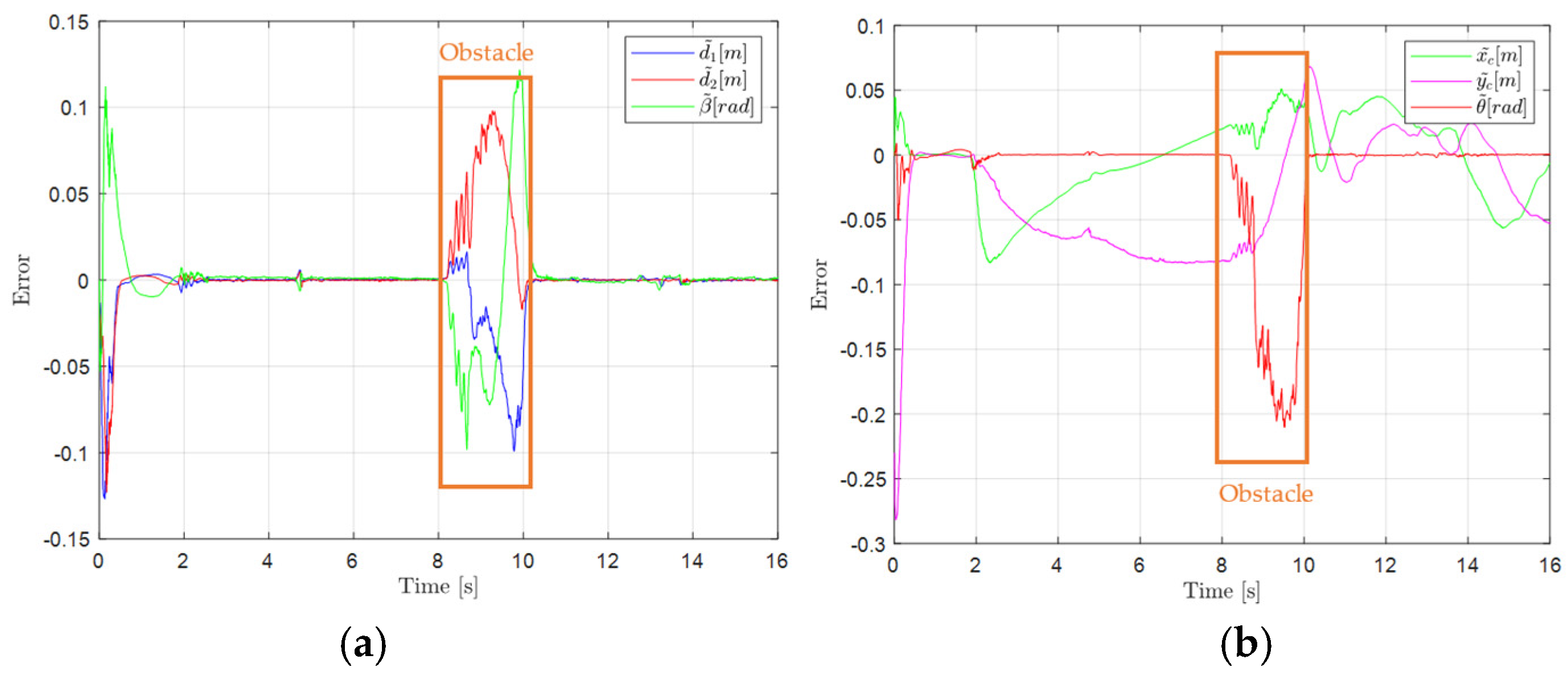
4. Experimental Tests and Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Slawiñski, E.; Santiago, D.; Mut, V. Dual coordination for bilateral teleoperation of a mobile robot with time varying delay. IEEE Lat. Am. Trans. 2020, 18, 1777–1784. [Google Scholar] [CrossRef]
- Tarn, T.; Bejczy, A.; Xi, N.; Ramadorai, A. Distributed control architecture for a sensor-driven dual arm system. Mechatronics 1994, 4, 481–502. [Google Scholar] [CrossRef]
- Patiño, K.; Slawiñski, E.; Moran-Armenta, M.; Mut, V.; Rossomando, F.G.; Moreno-Valenzuela, J. Neural networks in the delayed teleoperation of a skid-steering robot. Mathematics 2025, 13, 2071. [Google Scholar] [CrossRef]
- Karbasizadeh, N.; Aflakiyan, A.; Zarei, M.; Masouleh, M.T.; Kalhor, A. Dynamic identification of the Novint Falcon Haptic device. In Proceedings of the 2016 4th International Conference on Robotics and Mechatronics (ICROM), Tehran, Iran, 26–28 October 2016; pp. 518–523. [Google Scholar] [CrossRef]
- Renon, P.; Yang, C.; Ma, H.; Cui, R. Haptic interaction between human and virtual iCub robot using Novint Falcon with CHAI3D and MATLAB. In Proceedings of the 32nd Chinese Control Conference, Xi’an, China, 26–28 July 2013; pp. 6045–6050. [Google Scholar]
- Li, Y.; Chai, L.; Wu, C. Multi-robot formation obstacle avoidance based on virtual robots and improved artificial potential fields. In Proceedings of the 2024 China Automation Congress (CAC), Qingdao, China, 1–3 November 2024; pp. 1861–1866. [Google Scholar] [CrossRef]
- Xi, N.; Tarn, T.; Bejczy, A. Event-based planning and control for multi-robot coordination. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Atlanta, GA, USA, 2–6 May 1993; Volume 1, pp. 251–258. [Google Scholar] [CrossRef]
- Lima, A.; Gouvea, J.A.; Lizarralde, F.; Hsu, L. Trajectory tracking, pose regulation and adaptive formation control of a group of nonholonomic mobile robots. IFAC Proc. Vol. 2014, 47, 5709–5714. [Google Scholar] [CrossRef]
- Zolotas, A.; Antonelli, G.; Chiaverini, S. A survey on formation control in robotics. Annu. Rev. Control. 2019, 48, 242–249. [Google Scholar] [CrossRef]
- Jacob M, J.; Dinesh, A.; Mulla, A.K. On bilateral teleoperation of multi-agent systems: Bearing-based formation tracking control. In Proceedings of the 2022 Eighth Indian Control Conference (ICC), Chennai, India, 14–16 December 2022; pp. 67–72. [Google Scholar] [CrossRef]
- Riera, J.; Daquilema, E.; Andaluz, G.M.; Leica, P. Teleoperation of the TurtleBot Mobile Robot using an SMC controller in environments with obstacles. In Proceedings of the 2024 IEEE Eighth Ecuador Technical Chapters Meeting (ETCM), Cuenca, Ecuador, 15–18 October 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Dong, N.; Hu, J.; Li, J.; Shi, J.; Tan, L.; Lin, Y. A Position-Based Impedance Control Strategy of Bilateral Teleoperation System with Force Feedback. In Proceedings of the 2021 China Automation Congress (CAC), Beijing, China, 22–24 October 2021; pp. 6924–6929. [Google Scholar] [CrossRef]
- Neumann, M.A.; Kitts, C.A. A hybrid multirobot control architecture for object transport. IEEE/ASME Trans. Mechatron. 2016, 21, 2983–2988. [Google Scholar] [CrossRef]
- Cheong, J.; Niculescu, S.-I. Robust motion synchronization control for interconnected systems with human interaction. IFAC Proc. Vol. 2008, 41, 6347–6352. [Google Scholar] [CrossRef]
- Leica, P.; Rivera, K.; Muela, S.; Chavez, D.; Andaluz, G.; Andaluz, V.H. Consensus algorithms for bidirectional teleoperation of aerial manipulator robots in an environment with obstacles. In Proceedings of the 2019 IEEE Fourth Ecuador Technical Chapters Meeting (ETCM), Guayaquil, Ecuador, 11–15 November 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Andaluz, G.M.; Andaluz, V.H.; Terán, H.C.; Arteaga, O.; Chicaiza, F.A.; Varela, J.; Ortiz, J.S.; Pérez, F.; Rivas, D.; Sánchez, J.S.; et al. Modeling dynamic of the human-wheelchair system applied to NMPC. In Intelligent Robotics and Applications; Springer: Cham, Switzerland, 2016; pp. 179–190. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cabrera, J.; Andaluz, G.M.; Leica, P.; Camacho, O. Bilateral Teleoperation of a Formation of Mobile Robot Using Proportional Control and Obstacle Avoidance: Experimental Results. Eng. Proc. 2025, 115, 10. https://doi.org/10.3390/engproc2025115010
Cabrera J, Andaluz GM, Leica P, Camacho O. Bilateral Teleoperation of a Formation of Mobile Robot Using Proportional Control and Obstacle Avoidance: Experimental Results. Engineering Proceedings. 2025; 115(1):10. https://doi.org/10.3390/engproc2025115010
Chicago/Turabian StyleCabrera, Juan, Gabriela M. Andaluz, Paulo Leica, and Oscar Camacho. 2025. "Bilateral Teleoperation of a Formation of Mobile Robot Using Proportional Control and Obstacle Avoidance: Experimental Results" Engineering Proceedings 115, no. 1: 10. https://doi.org/10.3390/engproc2025115010
APA StyleCabrera, J., Andaluz, G. M., Leica, P., & Camacho, O. (2025). Bilateral Teleoperation of a Formation of Mobile Robot Using Proportional Control and Obstacle Avoidance: Experimental Results. Engineering Proceedings, 115(1), 10. https://doi.org/10.3390/engproc2025115010




