Design Considerations of a Vibration Absorber with Nonlinear Stiffness for Power Electric Units ^†

Abstract

Power electronic units (PEUs) in electric drivetrains are subjected to vibration loads that may lead to component fatigue through resonance. This research aims to understand the behavior of passive vibration absorbers and to establish a design approach for them. The proposed systematic design of a nonlinear tuned mass damper (NTMD) for PEUs begins with the separate linear experimental analyses of the PEU and passive absorber. This linear approach is possible due to the Hartman–Grobman theorem. Then the nonlinearity is quantified through frequency sweep measurements. A two-degree-of-freedom (DoF) coupled model is developed for the NTMD, which can be used for analyzing certain parameter changes. To manage the load-dependent responses inherent to nonlinear behavior, design constraints on the attenuated bandwidth and absorber stiffness are introduced, providing clear and optimizable targets. By extending classical linear absorber design principles to nonlinear regimes, the proposed method enhances the durability and reliability of PEU components.

1. Introduction

In the field of hybrid and electric vehicles, the power electronic unit (PEU), commonly referred to as the inverter, serves as a critical component that plays an essential role in the overall functionality and performance of the vehicle [1]. Its primary function is to convert the direct current (DC) supplied by the battery into alternating current (AC) that powers the electric machine. The reliability and efficiency of the PEU are crucial, as they directly influence the vehicle’s overall performance, energy efficiency, and user experience. Given that PEUs are typically mounted directly onto or in close proximity to the electric engine, vibration, alongside thermomechanical effects become a significant concern that must be addressed [2]. Excessive vibrations can lead to premature wear and fatigue of components, ultimately reducing the lifespan of a PEU and affecting the vehicle’s operational reliability. Therefore, it is crucial that during the design phase of the PEU, greater emphasis is placed on developing designs that are robust against vibration. This can be achieved by strategically shifting resonance frequencies away from critical regions or by incorporating effective damping elements to reduce amplitude [3]. Passive vibration absorbers, including tuned mass dampers (TMDs) and viscous dampers, provide effective, maintenance-free solutions that can significantly reduce resonant responses in various applications [3]. These absorbers offer advantages over traditional solutions by minimizing the need for active control systems and reducing maintenance requirements.

This study aims to briefly cover the fundamental principles of designing TMDs [3,4], by proposing a systematic step-by-step design procedure, and highlight the crucial role of mass ratio in determining the overall performance of the system. The attached absorber shows significant nonlinear behavior in this study. Therefore, our systematic proposition considers a nonlinear tuned mass damper (NTMD) [5], where load-dependent response curves are extracted for the coupled system, consisting of the PEU and the nonlinear absorber. To tune the NTMD, our proposition suggests the extraction of locally (small amplitude vibrations) linear parameters first [6]. Then, the experimental identification of the nonlinear parameter is carried out [7]. Finally, the absorber is designed through numerical simulations on the identified mechanical structure. Here, we constrain the frequency range and the stiffness of the absorber to obtain a clear and optimizable set of parameters.

The remainder of this study consists of the brief introduction of linear TMD design considerations. Then, the systematic nonlinear identification of the absorber and the tuning of the NTMD is discussed in detail. We show this procedure through the mass tuning of a given absorber within a predefined frequency range. Finally, a summary of our findings is shown to the reader.

2. Design Considerations of Linear Vibration Absorbers

Vibration absorbers play a critical role in engineering systems by reducing undesirable vibrations, protecting equipment, enhancing performance, and improving comfort and safety. The precise design of TMDs [3] ensures efficient vibration mitigation in mechanical structures, with the primary goal to minimize the response amplitude of the primary structure, $m_1$ in Figure 1. Achieving this goal involves optimizing several parameters, such as the damping coefficient, mass ratio, stiffness, natural frequencies and the mounting location. This section will briefly discuss these factors and present guidelines for effectively sizing linear TMDs.

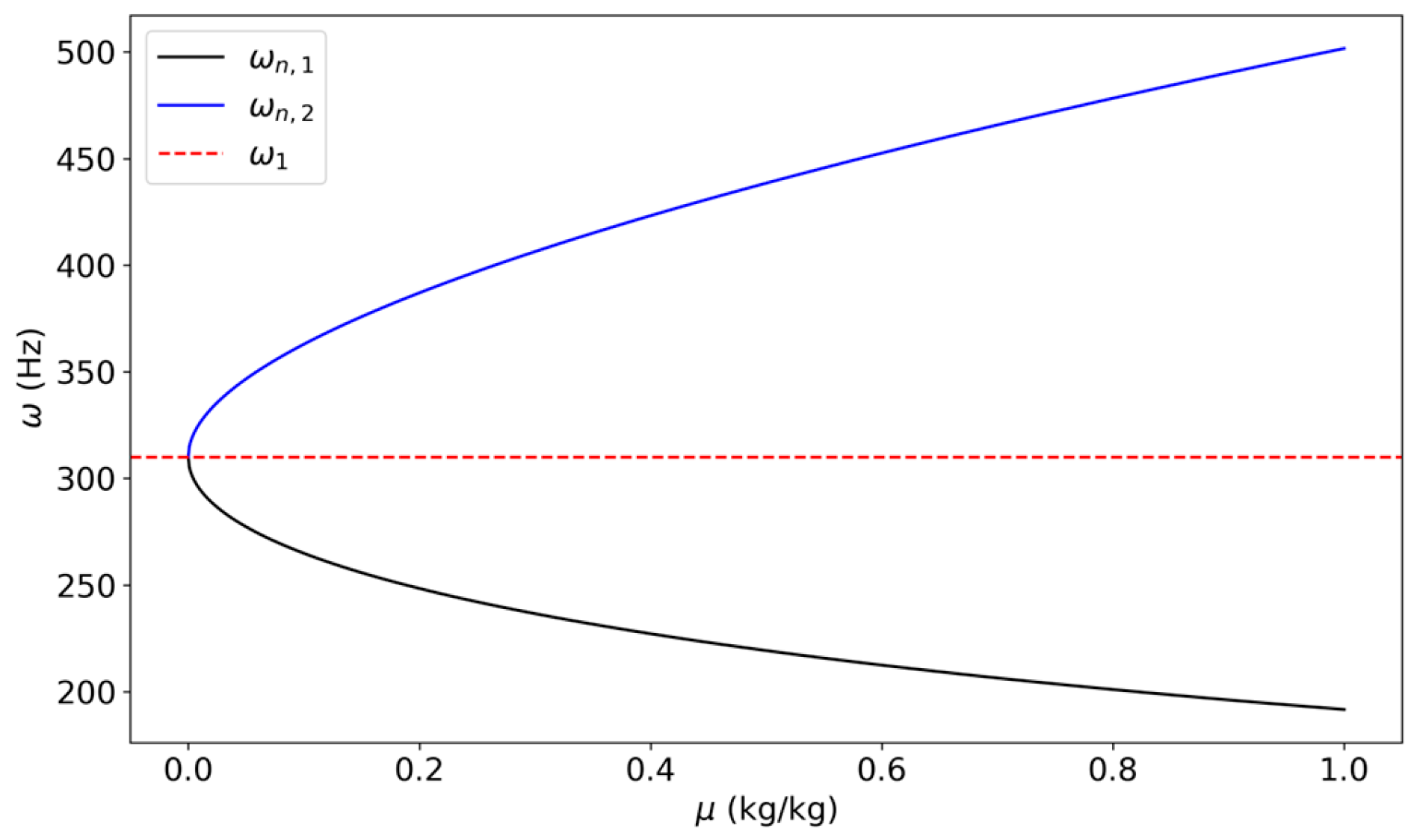
The mass ratio $\mu$ is defined as the relation between the added absorber mass $m_2$ and the original mass $m_1$, visualized in Figure 1c. Typically, a higher mass ratio improves the bandwidth of the vibration attenuation on the primary structure $m_1$. However, excessively high mass ratios can negatively affect the overall system by introducing an unfeasible mass, increasing costs, and neglecting practicality. Optimal mass ratios usually range between 0.05 and 0.2 in practice, balancing efficiency and feasibility. This study builds on the mechanical model, introduced in Figure 1c. The mathematical formulation of this model can be written as

$$\begin{gathered} m_1{\ddot{x}}_1+c_1{\dot{x}}_1+c_2\left({\dot{x}}_1-{\dot{x}}_2\right)+k_1{x}_1+k_2\left(x_1-x_2\right)=F_1\left(t\right), \\ {m}_2{\ddot{x}}_2+c_2\left({\dot{x}}_2-{\dot{x}}_1\right)+k_2\left(x_2-x_1\right)=0, \end{gathered}$$

(1)

where $m_1$, $k_1$, and $c_1$ are the apparent mass, stiffness and damping coefficient of the attenuated structure, respectively. The external force in the structure is defined as $F_1\left(t\right)≔F_{\mathrm{1,1}} \mathrm{c}\mathrm{o}\mathrm{s} {\omega }_{\mathrm{F}}t$ Similarly, $m_2$, $k_2$, and $c_2$ are the parameters regarding the standalone absorber mass (Figure 1a,b). The displacements of the two masses are denoted by $x_1$ and $x_2$, respectively. Finally, the forcing amplitude, acting on $m_1$, is $F_1$, with $\omega$ forcing angular frequency. The system parameters are extracted through conventional modal testing techniques and summarized in

Table 1. Original system parameters from the experimental modal analysis of the TMD for the linear regime. After tuning the antiresonance to be at the resonance of the original structure $m_2=0.364 \mathrm{k}\mathrm{g}$.

	${\mathit{m}}_{\mathit{i}}$ (kg)	${\mathit{k}}_{\mathit{i}}$ (N/m)	${\mathit{c}}_{\mathit{i}}$ (Ns/m)	Driving Force:
$i=1$	$5.979$	$24·{10}^6$	$646.9$	$\omega \in [200, 400]$ Hz
$i=2$	$0.2$	$1.46·{10}^6$	$21.6$	$F_{\mathrm{1,1}}\in [1, 200]$ N

.

Then, the formulation of the mass ratio μ and the dimensionless squared normalized frequency $\mathsf{\Omega }$ are written as

$$\mu :={\displaystyle \frac{m_2}{m_1}}, \mathsf{\Omega }:={\displaystyle \frac{{\omega }_n^2}{{\omega }_1^2}} ,$$

(2)

where ${\omega }_1$ is the natural frequency of the standalone structure (${\omega }_1^2=k_1/m_1$), while $m_1$, and ${\omega }_n$ is the natural frequency of the coupled structure. For showing the basic principle of primary system response minimalization, let $c_1$ and $c_2$ be zero. In such a case, the response displacement of the primary mass $m_1$ is

$$H_{11}\left(\omega \right)≔{\displaystyle \frac{F_1\left(\omega \right)}{x_1\left(\omega \right)}}={\displaystyle \frac{-{\omega }^2{m}_2+k_2}{\left(-{\omega }^2{m}_1+k_1+k_2\right) \left(-{\omega }^2{m}_2+k_2\right)-k_2^2}},$$

(3)

where $H_{11}$ (forcing and response are both at $m_1$) denotes the frequency response function (FRF) of (1) without any damping. The response amplitude of $m_1$ is minimized when the absorber parameters $m_2$ and $k_2$ are tuned close to the primary system’s natural frequency [3]. Mathematically, optimal tuning occurs when

$$\left(-{\omega }^2{m}_2+k_2\right)=0.$$

(4)

This means that the TMD must be tuned to the resonant frequency of the standalone structure:

$${\displaystyle \frac{k_2}{m_2}}={\displaystyle \frac{k_1}{m_1}}.$$

(5)

Introducing the absorber will create a coupled system, where the first resonance of the new system is ${\omega }_{n,1}$ and the second is ${\omega }_{n,2}$ (with the target ratio: $\mathsf{\Omega }≔{\omega }_{n,\mathrm{1,2}}^2/{\omega }_1^2$) in such order that ${\omega }_{n,1}<{\omega }_1<{\omega }_{n,2}$; see Figure 2 and Figure 3. Combining (1) and (2) after simplification and setting $F_{\mathrm{1,1}}=0$ in (1), leads to the following characteristic equation:

$${\mathsf{\Omega }}^2-\left(2+\mu \right)\mathsf{\Omega }+1=0.$$

(6)

Using the quadratic formula and exploiting $\mathsf{\Omega }{\omega }_1^2={\omega }_n^2$ lead to the following:

$${\omega }_{n,\mathrm{1,2}}^2={\omega }_1^2\left(1+{\displaystyle \frac{\mu }{2}}\pm \sqrt{\mu +{\displaystyle \frac{{\mu }^2}{4}}}\right).$$

(7)

This means that the two coupled natural frequencies ${\omega }_{n,1}$ and ${\omega }_{n,2}$ are split approximately symmetrically around the standalone ${\omega }_1$ when $\mu$ << 1. Then each offset is approximately $1/2\sqrt{\mu } {\omega }_1$. However, for larger mass ratios, the offset becomes asymmetric as Figure 2 shows. Note that the greater mass ratio will make wider frequency splits, suggesting a more effective absorber design as in Figure 2.

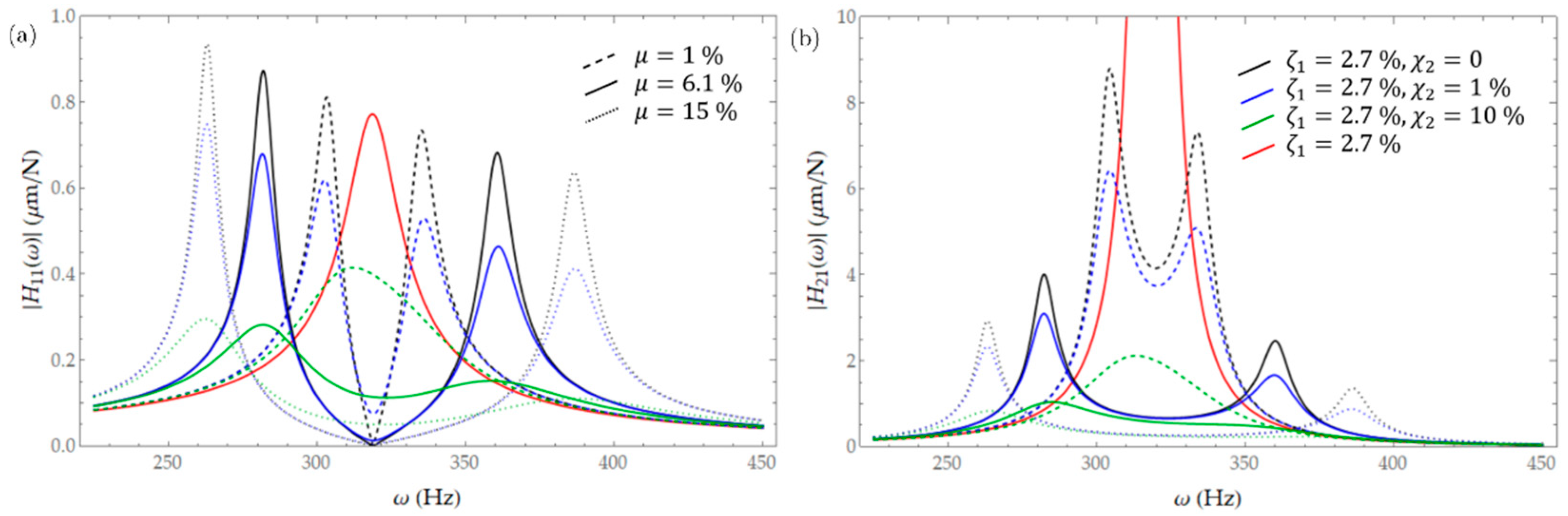
The damping coefficient $c_1$ determines the rate of the vibrational energy dissipation from the standalone structure, which usually results in a low standalone damping ratio (${\zeta }_1$ = 0.1% to 20%), causing the actual problematic peak in the first place (see red curves in Figure 3 with ${\zeta }_1=2.7\%$).

The TMD’s damping $c_2$ is a design parameter, which is historically defined to the standalone natural frequency of the structure as ${\chi }_2:=c_2/\left({2m}_2{\omega }_1\right)$ [3]. Increasing ${\chi }_2$, the validity of (4) gradually decreases. In fact, ideally, we prefer this value to be vanished as (3) suggests; however uncertainties in the structural properties require increased bandwidth in so-called antiresonance attenuation. This can be achieved with moderate added damping through ${\chi }_2$. One can assume any damping is welcomed; however it must be kept at least under, e.g., one of the lowest invariant points in the Den Hartog sense [3] to actually have antiresonance, resulting in

$${\chi }_2^2<{\chi }_{2,\mathrm{c}\mathrm{r}}^2≔{\displaystyle \frac{\mu \left(2+\mu \right)}{4 \left(1+\mu \right)\left(1+\mu +2 \sqrt{\mu \left(2+\mu \right)}\right)}}.$$

(8)

With the presented data in Table 1, this limiting Den Hartog’s damping factor is ${\chi }_2<{\chi }_{2,\mathrm{c}\mathrm{r}}=13 \%$ with mass ratio $\mu =6.1 \%$ which is determined with the tuned mass $m_2=0.364 \mathrm{k}\mathrm{g}$ according to (5). In Figure 3, different FRFs are depicted related to the direct (driving) ones in the structure H₁₁(ω) (Figure 3a) and the cross-FRF H₂₁(ω) (Figure 3b) between the structure and the TMD showing its relative motion to the structure. The different mass ratios are shown with different line styles ($\mu =\left(1, 6.1, 15.0\right)\%$, (dashed, continuous, dotted)), while different TMD damping ratios in Den Hartog sense are shown with black, blue and green colors in an order of ${\chi }_2=\left(0, 1, 10\right)\%$.

One can realize all of the presented cases have antiresonance except the one with the lowest mass ratio with the highest damping for the TMD ${\chi }_2$, when $\mu =1\%$ and ${\chi }_2=10\%$ for which the critical damping was ${\chi }_{2,\mathrm{c}\mathrm{r}}=6.2 \%$ according to (8).

3. Design Considerations of Nonlinear Vibration Absorbers

Although designing linear TMDs is a common and well-developed field in engineering [3,4], the materials used (especially rubber) can lead to nonlinear behavior for high forcing amplitudes [7]. Then, the effective design of a nonlinear tuned mass damper (NTMD) [5] becomes more challenging as the resonance depends on the forcing amplitude [8]. For this particular example, in this study, we assume the following equations of motion, based on the model in Figure 1:

$$\begin{gathered} m_1{\ddot{x}}_1+c_1{\dot{x}}_1+c_2\left({\dot{x}}_1-{\dot{x}}_2\right)+k_1{x}_1+k_2\left(x_1-x_2\right)+\beta {\left(x_1-x_2\right)}^3=F_{\mathrm{1,1}} \mathrm{c}\mathrm{o}\mathrm{s} \omega t, \\ {m}_2{\ddot{x}}_2+c_2\left({\dot{x}}_2-{\dot{x}}_1\right)+k_2\left(x_2-x_1\right)+\beta {\left(x_2-x_1\right)}^3=0, \end{gathered}$$

(9)

where the only difference from (1) is the non-zero nonlinear parameter $\beta$. This way, the system is coupled through the combined linear $k_2$ and nonlinear $\beta$ springs.

Finding an optimal or efficient parameter set for the nonlinear vibration absorber is not a straightforward task as was in Section 2 or in [3,4]. First, we have to characterize the nonlinearity of the single DoF absorber

$$m_2\ddot{x}+c_2\dot{x}+k_{2}x+\beta x^3=F_2 \mathrm{c}\mathrm{o}\mathrm{s} \omega t,$$

(10)

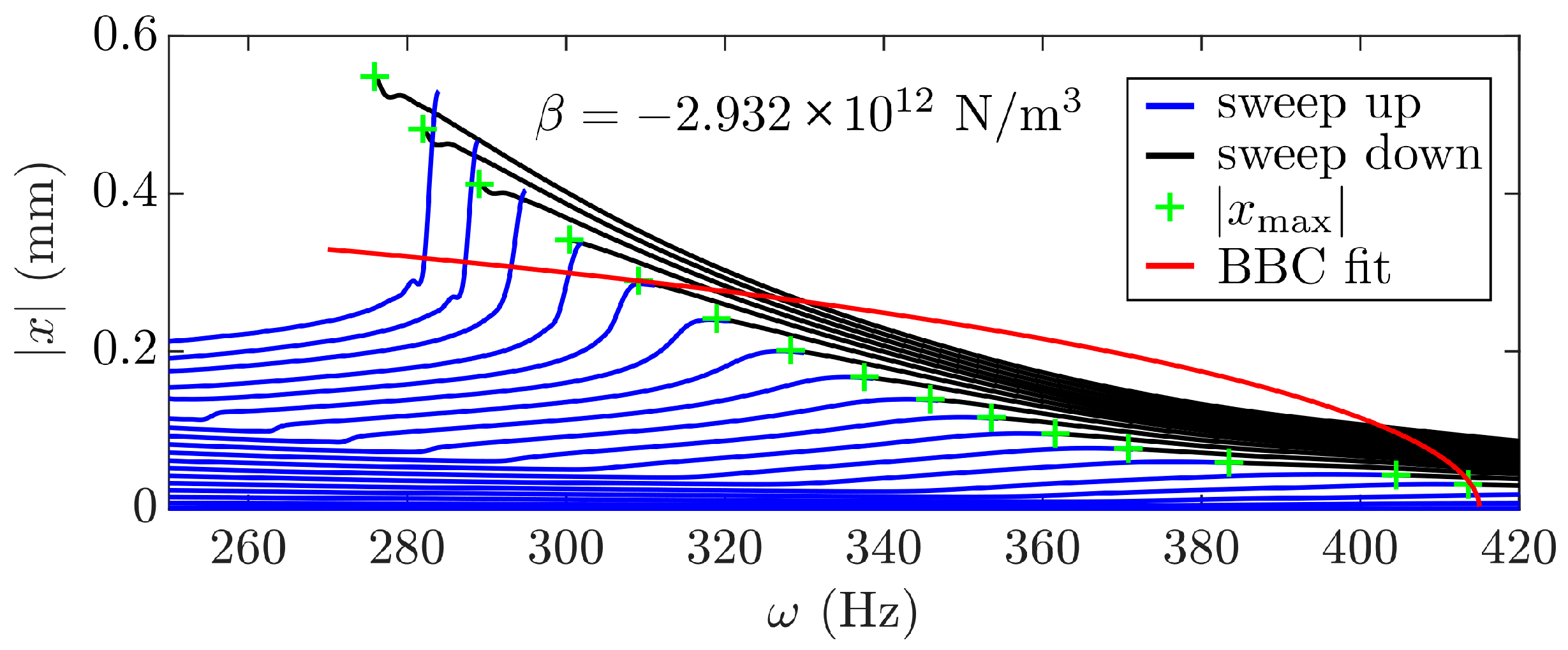
which is already challenging in most cases [7,9]. Two key features are usually extracted to describe vibrating nonlinear structures. First, the so-called backbone curve (BBC) [8] (see Figure 4) which describes the vibration amplitude as a function of the vibration frequency during a free decay [8]. Secondly, the nonlinear frequency response curves (NLFR) (Figure 4) can be used for visualizing the shifting of the resonance frequency as the forcing amplitude grows [8]. Extracting these two features helps the parameter fitting of the mechanical system (8).

In this study, we use slow bi-directional frequency sweeps to extract the NLFR curves of the standalone vibration absorber (Figure 4). Note that these curves are only comparable with ideal nonlinear models like the one in (10) if the input force amplitude that excites the structure is constant [8]. Therefore, either a force controller must be used, or the measured curves must be resectioned [8] at constant forcing amplitudes. Then, the NLFR curves can be presented (as in Figure 4) for the nonlinear vibration absorber in Figure 1b). By picking the maximum amplitudes of the NLFR curves, we get a good approximation (green crosses in Figure 4) of the BBC if the damping is relatively low in the structure [10].

A cubic BBC can be fitted for the extracted data point by the following equation:

$$A\left(\omega \right)=2\sqrt{{\displaystyle \frac{{\omega }^2-{\omega }_1^2}{3\hspace{0.17em}\gamma }}},$$

(11)

derived from the Poincaré–Linstedt solution of an undamped Duffing oscillator [9]. Note that $\gamma ≔\beta /m$ is the normalized nonlinear parameter, and $A\left(\omega \right)$ is the BBC of the standalone vibration absorber with the local (linear) natural frequency ${\omega }_2$. The fitted curve for the extracted data is visualized in Figure 4. Although we acknowledge that the best fit for this case is not the cubic nonlinear oscillator, the simplicity of it enables us to qualitatively analyze the simplest case of a NTMD, which somewhat resembles the observed nonlinear absorber.

Having a grasp on the simplified mechanical model of the problem enables us to execute numerical simulations of the frequency sweeps that are related to the coupled structure, modeled by (9). To achieve an effective operation of the NTMD, one has to define goals to constrain the search for good passive absorber parameters ($m_2$ and $k_2$). For this particular case, we have set the following constraints:

• Attenuated frequency bandwidth: $\omega \in \left[200, 300\right]$ Hz.
• Feasible absorber mass range: $m_2\in \left[0.124, 0.5\right]$ kg.
• Forcing amplitude range: $F_{\mathrm{1,1}}\in \left[1, 300\right]$ N.
• Goal: minimizing the response amplitude of $m_1$ within the suggested frequency bandwidth.

With a clear set of goals in mind, the numerical tests can be methodically executed to find the most effective solution for the problem at hand. We propose carrying out numerical frequency down-sweep tests, since this case is a softening nonlinearity, with $F_{\mathrm{1,1}}=1$ N and $m_2$ incremented from 0.124 kg until 0.5 kg between the frequency sweeps. From this set of numerical tests, store the maximum response amplitude of $x_1$ for every sweep. This procedure has to be repeated $M\in {\mathbb{N}}^{+}$ times, while we store the maximum values in a set $x_{1,\mathrm{m}\mathrm{a}\mathrm{x}}\in {\mathbb{R}}^{N\times M}$, where $N$ is the number of simulated sweeps and $M$ is the number of forcing amplitudes. Figure 5 shows the visual representation of $x_{1,\mathrm{m}\mathrm{a}\mathrm{x}}$ for both the linear (grey) and nonlinear (red) cases. By finding the minimum in $x_{1,\mathrm{m}\mathrm{a}\mathrm{x}}$ at every forcing amplitude, one can obtain the most feasible $m_2$ parameter for the different loads considered in this case. It can be observed that increasing the parameter $m_2$ significantly improves the attenuation capabilities of the absorber, meaning that for both the TMD and NTMD, the most effective absorber mass is $m_2=0.364$ kg with the set goals in mind.

Finally, let us demonstrate the difference between the TMD and NTMD with the chosen $m_2$ parameter. As shown in Figure 6, both absorbers are attenuating the response amplitudes within the frequency bandwidth of interest, with the addition of bistable regions in the nonlinear case. We also present the numerical continuation (executed in COCO [11]) of the NTMD for the observed case in Figure 7.

In summary, we proposed a methodical approach to first identify the linear subsystems and then the underlying nonlinearity of the absorber. Then fine-tuning of the NTMD parameters is possible through numerical simulations. We emphasize that there is no general solution to these problems. One has to set goals and constraints to achieve sufficient vibration attenuation with the introduced NTMD.

4. Conclusions

In this article, we demonstrate how to design a passive vibration absorber that attenuates the response amplitude of power electronic units at a given frequency band. First, the linear optimization is discussed. Then, the effective parameter selection of an NTMD is shown for the specific case with the PEUs.

A methodical approach is proposed, where one can set sufficient parameters for their NTMD design with given constraints in mind. First, the linear and nonlinear parameters have to be extracted for the accurate modeling of the observed coupled system. While the linear parameters can be addressed by small forcing amplitude measurement techniques related to the topic of experimental modal analysis, the nonlinear parameter extraction is rather challenging.

We used frequency sweeps with ensured constant forcing amplitudes to extract the phase resonance of the standalone absorber. After the system identification, a parameter analysis can be performed on the forcing amplitude and the mass ratio. By extracting the maximum response amplitudes of the attenuated system (within the frequency bandwidth of interest), an effective mass ratio can be found.