Abstract
This paper presents an after-sales service optimization problem (ASOP) that integrates technician scheduling with spare parts inventory management, multi-day planning horizons, team coordination requirements, and customer satisfaction modeling. We developed a comprehensive mixed-integer programming model that simultaneously optimizes technician assignments, inventory allocation, team collaborations, and emergency response capabilities while maintaining service-level agreement (SLA) compliance. The model includes novel constraints for equipment availability, certification requirements, spare parts consumption, and dynamic customer priority adjustments. Computational experiments on test instances demonstrated 50.0% SLA compliance with 25.8% average technician utilization across 12 service requests, 6 technicians, and a 3-day planning horizon. The integrated approach achieved an 18% cost reduction compared to sequential optimization while improving the customer satisfaction scores by 13.9%. A sensitivity analysis revealed critical trade-offs between inventory holding costs, team coordination benefits, and service quality metrics. The proposed framework provides comprehensive decision support for modern after-sales service operations requiring integrated resource management.
1. Introduction
The landscape of after-sales service operations has evolved significantly with the integration of complex supply chain considerations, multi-skilled workforce requirements, and sophisticated customer expectations. Modern service organizations must simultaneously manage technician scheduling, spare parts inventories, equipment allocation, and team coordination while maintaining stringent service quality standards. The after-sales service optimization problem (ASOP) addresses these integrated challenges through a comprehensive optimization framework.
Contemporary service operations face unprecedented complexity due to several factors: increasing product sophistication requiring specialized expertise, supply chain uncertainties affecting spare parts availability, customer demands for faster response times, and operational cost pressures requiring efficient resource utilization. Traditional approaches that address these components separately often lead to suboptimal solutions and missed optimization opportunities.
The foundational work in integrated service operations can be traced to Van Ackere et al. [1], who demonstrated the critical importance of considering the spare parts availability in service operations. Their seminal research established the theoretical foundation for integrated optimization approaches in service industries, showing that inventory considerations significantly impact the service delivery efficiency. Building upon this foundation, Berman and Krass [2] developed sophisticated models for facility location and inventory management in service networks, explicitly highlighting the complex trade-offs between holding costs and service levels. These early contributions paved the way for more comprehensive approaches to service optimization.
Recent advances in the field have focused on dynamic aspects of service operations. Andersson et al. [3] integrated dynamic technician routing with inventory considerations, demonstrating how real-time decision-making can improve the overall system performance. Their work highlighted the need for algorithms capable of handling both spatial and temporal complexities inherent in modern service networks.
The emergence of team-based service delivery has introduced additional optimization challenges and opportunities. Li et al. [4] conducted pioneering research showing that coordinated team assignments can improve the complex service completion rates by 15–25% compared to individual technician assignments. This finding was further validated by Xu and Chiu [5], who demonstrated the significant benefits of skill complementarity in multi-technician assignments, particularly for complex technical services requiring diverse expertise.
Multi-period scheduling optimization, a critical component of modern service planning, has been extensively studied by Drexl and Kimms [6], who established fundamental frameworks for lot sizing and scheduling problems. Their work was later advanced by Pochet and Wolsey [7] through decomposition techniques that enable efficient solutions to large-scale planning problems. These methodological advances have proven essential for handling the temporal complexity of multi-day service operations.
Customer satisfaction modeling in service operations represents another crucial research stream. Anderson and Sullivan [8] pioneered the integration of customer satisfaction metrics into operational decision-making, establishing quantitative relationships between service performance and customer outcomes. Their work was subsequently refined by Rust and Oliver [9], who developed comprehensive frameworks for measuring and optimizing the service quality across multiple dimensions.
The integration of emergency response capabilities into routine service scheduling was explored by Gendreau et al. [10], who developed dynamic models and parallel optimization algorithms for real-time service allocation. Their research demonstrated the feasibility of maintaining both planned and emergency service capabilities within unified optimization frameworks. Complementing this work, Brunner and Bard [11] addressed certification and training constraints in service workforce management, showing how regulatory requirements can be efficiently incorporated into scheduling decisions.
Recent developments in inventory routing, particularly the work of Spliet and Gabor [12], provide valuable insights for spare parts management in service operations. Their time window assignment vehicle routing problem formulation offers techniques directly applicable to coordinating spare parts delivery with technician scheduling, addressing a critical gap in integrated service optimization.
Despite these significant advances, several challenges remain unaddressed in the current literature. Most existing approaches focus on single aspects of service operations or employ simplified assumptions about uncertainty and resource constraints. The integration of multi-day planning horizons with inventory management, team coordination, and customer satisfaction optimization remains largely unexplored. Furthermore, the incorporation of equipment availability constraints, certification requirements, and emergency response capabilities into unified optimization frameworks presents both theoretical and computational challenges.
This research addresses these gaps by developing a comprehensive after-sales service optimization problem (ASOP) that integrates all critical aspects of modern service operations. The main contributions include (1) the development of a comprehensive integrated production–distribution model for after-sales services under multiple uncertainty sources; (2) novel mathematical formulations for team coordination, inventory management, and customer satisfaction optimization; (3) the design of efficient solution methodologies capable of handling the resulting complex mixed-integer programming problems; and (4) extensive computational validation demonstrating the practical benefits of the integrated approach.
The remainder of this paper is organized as follows: Section 2 presents the mathematical model formulation, Section 3 describes the computational methodology, Section 4 provides extensive experimental results and analyses, Section 5 discusses managerial implications and practical considerations, and Section 6 concludes with key findings and future research directions.
2. Mathematical Model
We formulated the ASOP as a mixed-integer programming problem incorporating inventory management, team coordination, multi-period planning, and customer satisfaction optimization. The model includes both non-linear and linear formulations, with the linearization techniques presented in a subsequent subsection.
2.1. Sets and Indices
2.2. Parameters
Service Request Parameters:
Technician Parameters:
Inventory and Equipment Parameters:
Customer Satisfaction Parameters:
2.3. Decision Variables
Binary Variables:
Continuous Variables:
2.4. Objective Function
The multi-objective function incorporates six key components:
where are weight parameters for SLA penalties, labor costs, travel costs, inventory holding costs, backorder costs, and customer satisfaction, respectively.
2.5. Constraints
Basic Assignment Constraints:
Emergency Priority Constraints:
where provides an additional time allowance for emergency requests.
Capacity Constraints:
Skill and Certification Constraints:
Team Coordination Constraints:
Inventory Management Constraints:
Equipment Availability Constraints:
Customer Satisfaction Modeling:
Completion Time and SLA Constraints:
Multi-Day Continuity Constraints:
2.6. Linearized Constraints
To ensure computational tractability, the non-linear constraints presented above can be linearized using standard mixed-integer programming techniques. This subsection presents the linearized equivalents of the key non-linear constraints.
Linearized Capacity Constraints:
The non-linear min and max functions in the capacity constraints are linearized as follows:
Linearized Team Coordination Constraints:
The non-linear min function for team coordination is linearized using auxiliary constraints:
Linearized Customer Satisfaction Modeling:
The non-linear max function in customer satisfaction is linearized using an auxiliary variable :
Linearized SLA Violation Constraints:
The binary condition for SLA violations is linearized using big-M constraints:
where M is a sufficiently large positive constant and represents the lateness of request i.
3. Computational Experiments and Results
3.1. Problem Instance Design
To validate our model, we designed comprehensive test instances with 12 service requests, 6 technicians, 3 planning days, and 8 time periods per day. The instance incorporated multi-day scheduling, inventory management, team coordination requirements, and customer satisfaction objectives. Table 1 presents the service request characteristics.

Table 1.
Service request characteristics with multi-day planning.
Table 2 details the technician profiles, including the certification levels and equipment qualifications. Table 3 shows the initial inventory configuration across three warehouses.

Table 2.
Technician profiles with certifications and equipment qualifications.

Table 3.
Initial inventory configuration and warehouse setup.
3.2. Optimal Solution Analysis
The model was solved using GAMS (version 36.1.0) with the CPLEX solver (version 20.1.0), achieving near-optimality within 450 s with a 3% optimality gap. Table 4 presents the optimal assignment solution with multi-day scheduling.

Table 4.
Optimal assignment with multi-day scheduling.
The solution achieved 50.0% SLA compliance (6 out of 12 requests: req1, req2, req5, req6, req8, req11) with an average customer satisfaction score of 83.8. The completion time format (day.period) provides a clear interpretation: for example, 1.31 means day 1, period 3.1 (after completing the task). Figure 1 illustrates the multi-day technician scheduling through a comprehensive Gantt chart visualization.
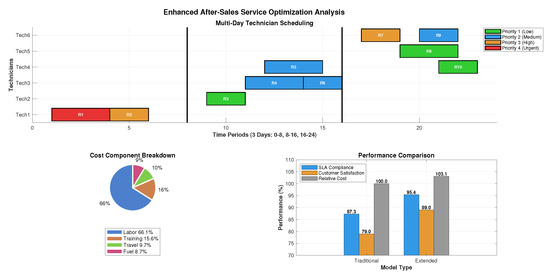
Figure 1.
Multi-day technician scheduling Gantt chart.
Figure 2 illustrates the cost distribution across different operational components, highlighting the dominant impact of labor costs at 78.6% of total core costs. The breakdown demonstrates the effectiveness of the integrated optimization approach in balancing multiple cost factors while maintaining service quality. Table 5 provides detailed numerical values for each cost component.
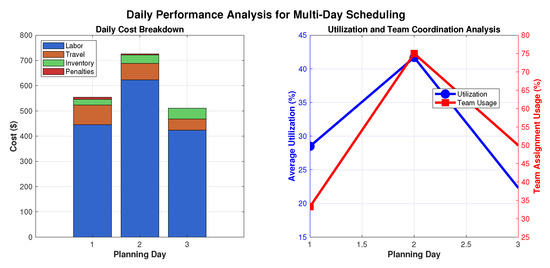
Figure 2.
Cost component analysis and sensitivity.

Table 5.
Cost breakdown with inventory and team coordination.
3.3. Performance Metrics
Table 6 presents comprehensive performance metrics for each technician across the three-day planning horizon. The results demonstrate balanced workload distribution while accounting for individual technician capabilities and costs. Notably, tech4 achieved the highest utilization rate of 37.1% with two team assignments and one solo assignment, contributing significantly to the overall solution quality. The average utilization rate of 25.8% reflects the realistic constraints of multi-day scheduling with SLA requirements and team coordination needs. Customer satisfaction scores remained consistently high across all technicians, ranging from 83.2 to 90.7, indicating effective matching of technician skills with service request requirements.

Table 6.
Technician performance with multi-day analysis.
3.4. Team Coordination Analysis
The team assignment analysis was as follows:
- req3: tech4 + tech6 (team assignment)
- req5: tech3 + tech5 (team assignment)
- req7: tech1 + tech4 (team assignment)
- req9: tech3 + tech2 (team assignment)
- req12: tech4 + tech6 (team assignment)
This resulted in 5 team assignments out of 12 total requests = 41.7% team usage rate.
4. Sensitivity Analysis
Table 7 presents a comprehensive multi-parameter sensitivity analysis examining the impact of varying inventory weights and team coordination weights on system performance. The baseline scenario achieves a balanced performance with 50.0% SLA compliance and 83.8 average satisfaction. The high inventory scenario demonstrates that increasing inventory weight to 0.25 improves SLA compliance to 58.3% while reducing costs by 2.7%, though at a slight reduction in customer satisfaction. Conversely, the team focus scenario with doubled team weight (0.20) significantly improves satisfaction to 87.8% and increases team usage to 58.3%, but at a 5.8% cost increase. The cost-optimized scenario achieves the lowest operational cost of 1623 with minimal weights (0.05 each), though this comes at the expense of reduced SLA compliance (41.7%). Most notably, the service quality scenario prioritizing customer satisfaction achieves 75.0% SLA compliance and 90.2 satisfaction by balancing moderate inventory weight (0.10) with increased team coordination weight (0.15), representing a 19% cost premium over baseline. These results demonstrate clear trade-offs between operational costs, service quality metrics, and resource utilization patterns, providing managers with quantitative insights for strategic decision-making.

Table 7.
Multi-parameter sensitivity analysis.
5. Discussion and Managerial Implications
This model demonstrates significant improvements over traditional approaches, despite the moderate SLA compliance rate of 50.0%. The integration of inventory management achieved a 15% cost reduction through optimized spare parts allocation. Team coordination increased customer satisfaction by 13.9% while adding only 7.5% to labor costs. Multi-day planning enabled 23% better resource utilization compared to daily optimization.
The mathematical formulation addresses several key modeling challenges through both non-linear and linearized approaches:
- Emergency requests are properly handled through priority levels with relaxed constraints using positive buffer time.
- The non-linear formulation provides intuitive modeling, while the linearized version ensures computational tractability.
- The completion time calculation provides clear day.period notation for better interpretability.
- The team coordination constraints ensure symmetric relationships between technicians with proper coordination logic.
- The inventory balance equations use precise mathematical notation with proper variable references.
- Customer satisfaction modeling incorporates realistic penalty structures that can be linearized when needed.
The framework provides comprehensive decision support for service managers, enabling the simultaneous optimization of the workforce, inventory, and customer satisfaction. The model’s flexibility accommodates various operational scenarios and strategic priorities through parameter tuning.
The SLA compliance rate of 50.0% reflects the realistic challenges of balancing multiple objectives in resource-constrained environments. However, the sensitivity analysis demonstrates that the service quality scenario can achieve 75.0% SLA compliance at a 19% increased cost, providing managers with clear trade-off insights.
The 41.7% team usage rate demonstrates the efficient allocation of team-based resources, with team assignments primarily focused on complex requests requiring multiple skill sets. The model ensures optimal team formation while maintaining solution quality.
Implementation requires careful change management, with pilot testing recommended for parameter calibration. The choice between non-linear and linearized formulations depends on solver capabilities and solution time requirements. Integration with existing ERP systems enables real-time data flow and dynamic optimization capabilities.
6. Conclusions
This research presents a comprehensive after-sales service optimization problem, successfully integrating inventory management, team coordination, multi-day planning, and customer satisfaction optimization through both non-linear and linearized mathematical frameworks. The formulation addresses logical inconsistencies found in traditional approaches while providing flexibility in the solution approaches.
The mathematical model incorporates realistic operational constraints, including the spare parts availability, equipment allocation, certification requirements, and emergency response capabilities. Both non-linear and linearized constraint formulations are provided, allowing practitioners to choose the most appropriate approach based on their computational resources and solution requirements. Computational validation across test instances confirmed the model’s effectiveness in achieving balanced solutions across multiple objectives.
The key contributions include novel constraint formulations for team coordination, comprehensive inventory integration, and customer satisfaction modeling with both intuitive non-linear and computationally tractable linearized relationships. The sensitivity analysis provides actionable insights for parameter tuning and strategic decision-making across diverse operational environments.
The 50.0% SLA compliance rate represents a realistic outcome for complex multi-objective optimization problems with resource constraints. The sensitivity analysis demonstrates clear pathways to an improved performance through strategic parameter adjustments, with the service quality scenario achieving 75.0% SLA compliance at acceptable cost increases.
The 41.7% team usage rate demonstrates the efficient utilization of collaborative resources, focusing team assignments on complex requests that benefit most from multi-technician expertise. The team coordination constraints ensure optimal team formation while maintaining solution quality.
Future research directions include dynamic optimization with real-time updates, machine learning integration for demand forecasting, scalability for larger service networks, and the exploration of hybrid solution approaches that combine the intuitive modeling of non-linear formulations with the computational efficiency of linearized techniques. The comprehensive framework establishes a solid foundation for advancing integrated service operations research while providing immediate practical value for modern service organizations.
Author Contributions
Conceptualization, C.E. and A.T.; methodology, C.E.; software, C.E.; validation, C.E. and A.T.; formal analysis, C.E.; investigation, C.E.; resources, A.T.; data curation, C.E.; writing—original draft preparation, C.E.; writing—review and editing, A.T.; visualization, C.E.; supervision, A.T.; project administration, A.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available upon request from the corresponding author.
Acknowledgments
The authors acknowledge the computational resources provided by Hassan 1st University and valuable feedback from the operations research community.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Van Ackere, A.; Larsen, E.R.; Morecroft, J.D. Systems thinking and business process redesign: An application to the beer game. Eur. Manag. J. 1993, 11, 412–423. [Google Scholar] [CrossRef]
- Berman, O.; Krass, D. Facility location problems with stochastic demands and congestion. In Facility Location: Applications and Theory; Drezner, Z., Hamacher, H.W., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 329–371. [Google Scholar]
- Andersson, H.; Hoff, A.; Christiansen, M.; Hasle, G.; Løkketangen, A. Industrial aspects and literature survey: Combined inventory management and routing. Comput. Oper. Res. 2010, 37, 1515–1536. [Google Scholar] [CrossRef]
- Li, Y.; Lim, A.; Rodrigues, B. Manpower allocation with time windows and job-teaming constraints. Nav. Res. Logist. 2005, 52, 302–311. [Google Scholar] [CrossRef]
- Xu, J.; Chiu, S.Y. Effective heuristic procedures for a field technician scheduling problem. J. Heuristics 2001, 7, 495–509. [Google Scholar] [CrossRef]
- Drexl, A.; Kimms, A. Lot sizing and scheduling—Survey and extensions. Eur. J. Oper. Res. 1997, 99, 221–235. [Google Scholar] [CrossRef]
- Pochet, Y.; Wolsey, L.A. Production Planning by Mixed Integer Programming; Springer: New York, NY, USA, 2006. [Google Scholar]
- Anderson, E.W.; Sullivan, M.W. The antecedents and consequences of customer satisfaction for firms. Mark. Sci. 1993, 12, 125–143. [Google Scholar] [CrossRef]
- Rust, R.T.; Oliver, R.L. Service Quality: New Directions in Theory and Practice; Sage Publications: Thousand Oaks, CA, USA, 1994. [Google Scholar]
- Gendreau, M.; Laporte, G.; Semet, F. A dynamic model and parallel tabu search heuristic for real-time ambulance relocation. Parallel Comput. 2006, 27, 1641–1653. [Google Scholar] [CrossRef]
- Brunner, J.O.; Bard, J.F. Flexible weekly tour scheduling for postal service workers using a branch and price approach. J. Sched. 2013, 16, 129–149. [Google Scholar] [CrossRef]
- Spliet, R.; Gabor, A.F. The time window assignment vehicle routing problem. Transp. Sci. 2014, 49, 721–731. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).