Bi-Objective Production–Distribution Planning for Paper Manufacturing: A Credibility-Based Expected Value Approach ^†

Abstract

The paper manufacturing industry faces increasing challenges in balancing operational costs with service quality under uncertain market conditions. This research presents a bi-objective credibility-based expected value model for integrated production–distribution planning that simultaneously minimizes total costs and maximizes service-level performance. The model considers multiple paper grades, production facilities, warehouses, and customer zones while handling demand uncertainty through credibility theory. Three additional constraints are introduced: service time limitations, capacity expansion decisions, and quality assurance requirements. The Torabi–Hassini (TH) method is employed to solve the bi-objective optimization problem effectively. Computational experiments demonstrate the model’s capability to provide balanced trade-off solutions between cost efficiency and service quality, achieving service-level improvements of 8–13% with cost increases of 5–9% compared to cost-only optimization, and cost reductions of 10–15% compared to service-only optimization. The results show that the credibility-based expected value approach provides robust and practical solutions for paper manufacturing supply chain optimization.

1. Introduction and Literature Review

The global paper manufacturing industry, valued at over USD 350 billion annually, plays a crucial role in supporting various economic sectors including packaging, publishing, and construction materials. With increasing environmental regulations, fluctuating raw material costs, and evolving customer expectations for service quality, paper manufacturers face complex challenges in optimizing their supply chain operations.

Traditional production–distribution planning models in paper manufacturing have primarily focused on cost minimization while treating service level as a constraint [1]. However, in today’s competitive market, service-level performance has become a critical differentiator that directly impacts customer satisfaction, retention, and long-term profitability. The challenge lies in finding optimal trade-offs between operational costs and service quality under uncertain demand conditions.

Multi-objective optimization in supply chain management has received considerable attention in recent years [2]. The bi-objective approach combining cost minimization with service-level maximization addresses the fundamental trade-off that manufacturing companies face in balancing operational efficiency with customer satisfaction. Altiparmak et al. [2] demonstrated the effectiveness of genetic algorithms for multi-objective supply chain network optimization, showing that simultaneous consideration of conflicting objectives provides superior solutions compared to sequential optimization approaches.

Service-level optimization in manufacturing has been studied from various perspectives. Some researchers focus on fill rate optimization, while others consider delivery time performance or demand satisfaction rates [3]. Jayaraman and Pirkul [3] developed comprehensive models for planning and coordination of production and distribution facilities, highlighting the importance of service-level considerations in facility location and capacity planning decisions.

Fuzzy set theory [4] and credibility theory [5] have proven effective in handling uncertainty in supply chain optimization. The credibility-based expected value model offers a computationally efficient approach that converts fuzzy parameters into deterministic equivalents while preserving the uncertainty structure of the original problem. Liu and Liu [5] established the theoretical foundation for expected value models under fuzzy uncertainty, providing a practical framework for decision-making when probability distributions are not available or appropriate.

The expected value model under fuzzy uncertainty provides a robust framework for handling imprecise demand information commonly encountered in industrial applications [6]. Peidro et al. [6] provided a comprehensive review of quantitative models for supply chain planning under uncertainty, demonstrating that fuzzy approaches often outperform stochastic methods when historical data is limited or unreliable.

The Torabi–Hassini (TH) method [7] has emerged as an effective approach for solving bi-objective optimization problems. Unlike traditional weighted sum or $ϵ$-constraint methods, the TH approach provides a more balanced treatment of objective functions and allows decision makers to express preferences through intuitive parameters. Torabi and Hassini [7] demonstrated that their interactive possibilistic programming approach generates well-distributed Pareto-optimal solutions while maintaining computational efficiency.

Paper manufacturing optimization has unique characteristics including grade-dependent setup costs, sequence-dependent changeovers, and quality requirements [1]. Santos and Almada-Lobo [1] developed integrated pulp and paper mill planning models that capture the complex production processes and quality constraints specific to the paper industry. The integration of capacity expansion decisions adds strategic planning elements to the tactical production–distribution model.

Recent studies have addressed uncertainty in production planning [8], but few have considered the bi-objective nature of cost-service trade-offs in paper manufacturing. Mula et al. [8] reviewed various models for production planning under uncertainty, identifying gaps in multi-objective approaches that simultaneously consider cost efficiency and service performance.

Credibility-based fuzzy mathematical programming has been successfully applied to various supply chain problems [9], demonstrating its effectiveness in handling epistemic uncertainty. Pishvaee et al. [9] developed credibility-based models for green logistics design, showing that this approach provides robust solutions while maintaining computational tractability.

The integration of production and distribution decisions with explicit consideration of service-level objectives represents a significant advancement in paper manufacturing optimization. Unlike previous approaches that treat these aspects separately [10], our integrated model captures the complex interdependencies between production scheduling, inventory management, distribution planning, and service quality performance.

This research addresses the following key contributions:

1.

Development of a bi-objective credibility-based expected value model for paper manufacturing that simultaneously optimizes costs and service levels.

2.

Introduction of three additional practical constraints: service time limitations, capacity expansion decisions, and quality assurance requirements.

3.

Application of the Torabi–Hassini (TH) method for effective multi-objective optimization.

4.

Comprehensive computational analysis demonstrating cost-service trade-offs and practical applicability.

The paper is organized as follows: Section 2 presents the mathematical model formulation, Section 3 describes the solution methodology using credibility theory and the TH method, Section 4 provides the computational results and analysis, and Section 5 concludes with the key findings and future research directions.

2. Mathematical Model Formulation

This section presents the bi-objective credibility-based expected value model for integrated production–distribution planning in paper manufacturing.

2.1. Sets and Indices

The following sets and indices are defined:

$$\begin{array}{cccc}\hfill P& =\{1,2,\dots ,p\}\hfill & \hfill & \mathrm{Set}\mathrm{of}\mathrm{paper}\mathrm{grades}\hfill \\ \hfill M& =\{1,2,\dots ,m\}\hfill & \hfill & \mathrm{Set}\mathrm{of}\mathrm{production}\mathrm{facilities}\hfill \\ \hfill W& =\{1,2,\dots ,w\}\hfill & \hfill & \mathrm{Set}\mathrm{of}\mathrm{warehouses}\hfill \\ \hfill C& =\{1,2,\dots ,c\}\hfill & \hfill & \mathrm{Set}\mathrm{of}\mathrm{customer}\mathrm{zones}\hfill \\ \hfill T& =\{1,2,\dots ,t\}\hfill & \hfill & \mathrm{Set}\mathrm{of}\mathrm{time}\mathrm{periods}\hfill \\ \hfill R& =\{1,2,\dots ,r\}\hfill & \hfill & \mathrm{Set}\mathrm{of}\mathrm{raw}\mathrm{materials}\hfill \\ \hfill P{M}_p& \subseteq M\hfill & \hfill & \mathrm{Set}\mathrm{of}\mathrm{facilities}\mathrm{capable}\mathrm{of}\mathrm{producing}\mathrm{grade}p\hfill \\ \hfill R{M}_p& \subseteq R\hfill & \hfill & \mathrm{Set}\mathrm{of}\mathrm{raw}\mathrm{materials}\mathrm{required}\mathrm{for}\mathrm{grade}p\hfill \end{array}$$

2.2. Parameters

2.2.1. Crisp Parameters

$$\begin{array}{cc}\hfill p{c}_{pmt}:& \mathrm{Production}\mathrm{cost}\mathrm{of}\mathrm{grade}p\mathrm{at}\mathrm{facility}m\mathrm{in}\mathrm{period}t\hfill \\ \hfill s{c}_{pmt}:& \mathrm{Setup}\mathrm{cost}\mathrm{for}\mathrm{grade}p\mathrm{at}\mathrm{facility}m\mathrm{in}\mathrm{period}t\hfill \\ \hfill h{c}_{mt}^p:& \mathrm{Holding}\mathrm{cost}\mathrm{of}\mathrm{grade}p\mathrm{at}\mathrm{facility}m\mathrm{in}\mathrm{period}t\hfill \\ \hfill h{c}_{wpt}^w:& \mathrm{Holding}\mathrm{cost}\mathrm{of}\mathrm{grade}p\mathrm{at}\mathrm{warehouse}w\mathrm{in}\mathrm{period}t\hfill \\ \hfill t{c}_{mwpt}^{mw}:& \mathrm{Transportation}\mathrm{cost}\mathrm{from}\mathrm{facility}m\mathrm{to}\mathrm{warehouse}w\mathrm{for}\mathrm{grade}p\mathrm{in}\mathrm{period}t\hfill \\ \hfill t{c}_{wcpt}^{wc}:& \mathrm{Transportation}\mathrm{cost}\mathrm{from}\mathrm{warehouse}w\mathrm{to}\mathrm{customer}c\mathrm{for}\mathrm{grade}p\mathrm{in}\mathrm{period}t\hfill \\ \hfill CA{P}_{mt}:& \mathrm{Production}\mathrm{capacity}\mathrm{of}\mathrm{facility}m\mathrm{in}\mathrm{period}t\hfill \\ \hfill WCA{P}_{wt}:& \mathrm{Storage}\mathrm{capacity}\mathrm{of}\mathrm{warehouse}w\mathrm{in}\mathrm{period}t\hfill \\ \hfill {\alpha }_{pr}:& \mathrm{Consumption}\mathrm{rate}\mathrm{of}\mathrm{raw}\mathrm{material}r\mathrm{for}\mathrm{grade}p\hfill \\ \hfill {\tau }_{pm}:& \mathrm{Processing}\mathrm{time}\mathrm{of}\mathrm{grade}p\mathrm{at}\mathrm{facility}m\mathrm{per}\mathrm{unit}\hfill \\ \hfill w_{cp}:& \mathrm{Weight}\mathrm{of}\mathrm{customer}c\mathrm{for}\mathrm{grade}p\mathrm{in}\mathrm{service}-\mathrm{level}\mathrm{calculation}\hfill \\ \hfill E{C}_{mt}:& \mathrm{Capacity}\mathrm{expansion}\mathrm{cost}\mathrm{at}\mathrm{facility}m\mathrm{in}\mathrm{period}t\hfill \\ \hfill S{T}_{wc}:& \mathrm{Service}\mathrm{time}\mathrm{from}\mathrm{warehouse}w\mathrm{to}\mathrm{customer}c\hfill \\ \hfill S{T}_{max}:& \mathrm{Maximum}\mathrm{allowable}\mathrm{service}\mathrm{time}\hfill \\ \hfill Q_{min}:& \mathrm{Minimum}\mathrm{quality}\mathrm{requirement}\hfill \end{array}$$

2.2.2. Fuzzy Parameters

$$\begin{array}{cc}\hfill {\tilde{D}}_{cpt}:& \mathrm{Fuzzy}\mathrm{demand}\mathrm{of}\mathrm{customer}c\mathrm{for}\mathrm{grade}p\mathrm{in}\mathrm{period}t\hfill \\ \hfill {\widetilde{RC}}_{rt}:& \mathrm{Fuzzy}\mathrm{cost}\mathrm{of}\mathrm{raw}\mathrm{material}r\mathrm{in}\mathrm{period}t\hfill \\ \hfill {\tilde{Q}}_{pmt}:& \mathrm{Fuzzy}\mathrm{quality}\mathrm{yield}\mathrm{of}\mathrm{grade}p\mathrm{at}\mathrm{facility}m\mathrm{in}\mathrm{period}t\hfill \\ \hfill {\tilde{A}}_{rt}:& \mathrm{Fuzzy}\mathrm{availability}\mathrm{of}\mathrm{raw}\mathrm{material}r\mathrm{in}\mathrm{period}t\hfill \end{array}$$

2.3. Decision Variables

$$\begin{array}{cc}\hfill X_{pmt}\ge 0:& \mathrm{Production}\mathrm{quantity}\mathrm{of}\mathrm{grade}p\mathrm{at}\mathrm{facility}m\mathrm{in}\mathrm{period}t\hfill \\ \hfill Y_{pmt}\in \{0,1\}:& \mathrm{Binary}\mathrm{setup}\mathrm{variable}\mathrm{for}\mathrm{grade}p\mathrm{at}\mathrm{facility}m\mathrm{in}\mathrm{period}t\hfill \\ \hfill Z_{mwpt}\ge 0:& \mathrm{Shipment}\mathrm{quantity}\mathrm{from}\mathrm{facility}m\mathrm{to}\mathrm{warehouse}w\mathrm{for}\mathrm{grade}p\mathrm{in}\mathrm{period}t\hfill \\ \hfill U_{wcpt}\ge 0:& \mathrm{Shipment}\mathrm{quantity}\mathrm{from}\mathrm{warehouse}w\mathrm{to}\mathrm{customer}c\mathrm{for}\mathrm{grade}p\mathrm{in}\mathrm{period}t\hfill \\ \hfill I_{mt}^p\ge 0:& \mathrm{Inventory}\mathrm{of}\mathrm{grade}p\mathrm{at}\mathrm{facility}m\mathrm{at}\mathrm{end}\mathrm{of}\mathrm{period}t\hfill \\ \hfill I_{wpt}^w\ge 0:& \mathrm{Inventory}\mathrm{of}\mathrm{grade}p\mathrm{at}\mathrm{warehouse}w\mathrm{at}\mathrm{end}\mathrm{of}\mathrm{period}t\hfill \\ \hfill V_{rt}\ge 0:& \mathrm{Procurement}\mathrm{quantity}\mathrm{of}\mathrm{raw}\mathrm{material}r\mathrm{in}\mathrm{period}t\hfill \\ \hfill E_{mt}\ge 0:& \mathrm{Capacity}\mathrm{expansion}\mathrm{at}\mathrm{facility}m\mathrm{in}\mathrm{period}t\hfill \\ \hfill S{L}_{cpt}\ge 0:& \mathrm{Service}-\mathrm{level}\mathrm{achievement}\mathrm{for}\mathrm{customer}c,\mathrm{grade}p\mathrm{in}\mathrm{period}t\hfill \end{array}$$

2.4. Bi-Objective Functions

Objective 1: Minimize Total Expected Cost

$$\begin{array}{cc}\hfill min{f}_1=& \sum _{p=1}^p\sum _{m=1}^m\sum _{t=1}^t(p{c}_{pmt}·X_{pmt}+s{c}_{pmt}·Y_{pmt}+h{c}_{mt}^p·I_{mt}^p)\hfill \\ \hfill & +\sum _{w=1}^w\sum _{p=1}^p\sum _{t=1}^{t}h{c}_{wpt}^w·I_{wpt}^w\hfill \\ \hfill & +\sum _{m=1}^m\sum _{w=1}^w\sum _{p=1}^p\sum _{t=1}^{t}t{c}_{mwpt}^{mw}·Z_{mwpt}\hfill \\ \hfill & +\sum _{w=1}^w\sum _{c=1}^c\sum _{p=1}^p\sum _{t=1}^{t}t{c}_{wcpt}^{wc}·U_{wcpt}\hfill \\ \hfill & +\sum _{r=1}^r\sum _{t=1}^{t}E\left[{\widetilde{RC}}_{rt}\right]·V_{rt}\hfill \\ \hfill & +\sum _{m=1}^m\sum _{t=1}^{t}E{C}_{mt}·E_{mt}\hfill \end{array}$$

(1)

Objective 2: Maximize Weighted Service Level

$$\begin{array}{c}\hfill max{f}_2={\displaystyle \frac{{\sum }_{c=1}^c{\sum }_{p=1}^p{\sum }_{t=1}^t{w}_{cp}·S{L}_{cpt}}{{\sum }_{c=1}^c{\sum }_{p=1}^p{\sum }_{t=1}^t{w}_{cp}}}\end{array}$$

(2)

2.5. Constraints

Production Capacity Constraints (with expansion):

$$\begin{array}{c}\hfill \sum _{p\in P{M}_m}{\tau }_{pm}·X_{pmt}\le CA{P}_{mt}+E_{mt},\forall m,t\end{array}$$

(3)

Production-Setup Linking Constraints:

$$\begin{array}{cc}\hfill X_{pmt}& \le M_{big}·Y_{pmt},\forall p,m,t\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill X_{pmt}& \ge 0,\forall p,m,t\hfill \end{array}$$

(5)

Facility Inventory Balance:

$$\begin{array}{c}\hfill I_{m,t-1}^p+X_{pmt}-\sum _{w=1}^w{Z}_{mwpt}=I_{mt}^p,\forall p,m,t\end{array}$$

(6)

Warehouse Inventory Balance:

$$\begin{array}{c}\hfill I_{wp,t-1}^w+\sum _{m=1}^m{Z}_{mwpt}-\sum _{c=1}^c{U}_{wcpt}=I_{wpt}^w,\forall w,p,t\end{array}$$

(7)

Warehouse Capacity Constraints:

$$\begin{array}{c}\hfill \sum _{p=1}^p{I}_{wpt}^w\le WCA{P}_{wt},\forall w,t\end{array}$$

(8)

Service-Level Definition (Corrected):

$$\begin{array}{c}\hfill S{L}_{cpt}·(E\left[{\tilde{D}}_{cpt}\right]+ϵ)=\sum _{w=1}^w{U}_{wcpt},\forall c,p,t\end{array}$$

(9)

where $ϵ>0$ is a small constant to avoid division by zero.

Raw Material Requirements:

$$\begin{array}{c}\hfill \sum _{r\in R{M}_p}{\alpha }_{pr}·V_{rt}\ge \sum _{m=1}^m{X}_{pmt},\forall p,t\end{array}$$

(10)

Raw Material Availability:

$$\begin{array}{c}\hfill V_{rt}\le E\left[{\tilde{A}}_{rt}\right],\forall r,t\end{array}$$

(11)

Service Time Limitations:

$$\begin{array}{c}\hfill \sum _{w=1}^{w}S{T}_{wc}·U_{wcpt}\le S{T}_{max}·\sum _{w=1}^w{U}_{wcpt},\forall c,p,t\end{array}$$

(12)

Capacity Expansion Limitations:

$$\begin{array}{c}\hfill E_{mt}\le 0.3·CA{P}_{mt},\forall m,t\end{array}$$

(13)

Quality Assurance Requirements:

$$\begin{array}{c}\hfill X_{pmt}·E\left[{\tilde{Q}}_{pmt}\right]\ge Q_{min}·Y_{pmt},\forall p,m,t\end{array}$$

(14)

Service-Level Bounds:

$$\begin{array}{c}\hfill 0\le S{L}_{cpt}\le 1,\forall c,p,t\end{array}$$

(15)

Non-negativity and Binary Constraints:

$$\begin{array}{cc}\hfill X_{pmt},Z_{mwpt},U_{wcpt},I_{mt}^p,I_{wpt}^w,V_{rt},E_{mt}& \ge 0\hfill \\ \hfill Y_{pmt}& \in \{0,1\}\hfill \end{array}$$

3. Solution Methodology

This section describes the credibility-based expected value approach and the Torabi–Hassini (TH) method for solving the bi-objective optimization problem.

3.1. Credibility-Based Expected Value Model

Following the credibility theory framework developed by Liu and Liu [5], for fuzzy parameters modeled as triangular fuzzy numbers $\tilde{\xi }=(a,b,c)$, the expected value using credibility theory is

$$\begin{array}{c}\hfill E\left[\tilde{\xi }\right]={\displaystyle \frac{a+2b+c}{4}}\end{array}$$

(16)

This formula provides a computationally efficient way to convert fuzzy parameters into deterministic equivalents while preserving the central tendency and uncertainty spread of the original fuzzy numbers.

For our fuzzy parameters, the expected value transformations are

$$\begin{array}{cc}\hfill E\left[{\tilde{D}}_{cpt}\right]& ={\displaystyle \frac{D_{cpt}^a+2D_{cpt}^b+D_{cpt}^c}{4}}\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill E\left[{\widetilde{RC}}_{rt}\right]& ={\displaystyle \frac{R{C}_{rt}^a+2R{C}_{rt}^b+R{C}_{rt}^c}{4}}\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill E\left[{\tilde{Q}}_{pmt}\right]& ={\displaystyle \frac{Q_{pmt}^a+2Q_{pmt}^b+Q_{pmt}^c}{4}}\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill E\left[{\tilde{A}}_{rt}\right]& ={\displaystyle \frac{A_{rt}^a+2A_{rt}^b+A_{rt}^c}{4}}\hfill \end{array}$$

(20)

where superscripts a, b, and c represent the lower, most likely, and upper values of the triangular fuzzy numbers, respectively.

3.2. Equivalent Deterministic Bi-Objective Model

By applying the expected value transformation to all fuzzy parameters, the model becomes the following:

Minimize:

$$\begin{array}{cc}\hfill f_1=& \sum _{p=1}^p\sum _{m=1}^m\sum _{t=1}^t(p{c}_{pmt}·X_{pmt}+s{c}_{pmt}·Y_{pmt}+h{c}_{mt}^p·I_{mt}^p)\hfill \\ \hfill & +\sum _{w=1}^w\sum _{p=1}^p\sum _{t=1}^{t}h{c}_{wpt}^w·I_{wpt}^w\hfill \\ \hfill & +\sum _{m=1}^m\sum _{w=1}^w\sum _{p=1}^p\sum _{t=1}^{t}t{c}_{mwpt}^{mw}·Z_{mwpt}\hfill \\ \hfill & +\sum _{w=1}^w\sum _{c=1}^c\sum _{p=1}^p\sum _{t=1}^{t}t{c}_{wcpt}^{wc}·U_{wcpt}\hfill \\ \hfill & +\sum _{r=1}^r\sum _{t=1}^t{\displaystyle \frac{R{C}_{rt}^a+2R{C}_{rt}^b+R{C}_{rt}^c}{4}}·V_{rt}\hfill \\ \hfill & +\sum _{m=1}^m\sum _{t=1}^{t}E{C}_{mt}·E_{mt}\hfill \end{array}$$

(21)

Maximize:

$$\begin{array}{c}\hfill f_2={\displaystyle \frac{{\sum }_{c=1}^c{\sum }_{p=1}^p{\sum }_{t=1}^t{w}_{cp}·S{L}_{cpt}}{{\sum }_{c=1}^c{\sum }_{p=1}^p{\sum }_{t=1}^t{w}_{cp}}}\end{array}$$

(22)

3.3. Torabi–Hassini (TH) Method

The TH method [7] converts the bi-objective problem into a single-objective one through the following steps:

Step 1: Determine $\alpha$-positive ideal solution ($\alpha$-PIS) and $\alpha$-negative ideal solution ($\alpha$-NIS) by solving each objective separately: $-(f_1^{\alpha -\mathrm{PIS}},x_1^{\alpha -\mathrm{PIS}})$ and $(f_2^{\alpha -\mathrm{PIS}},x_2^{\alpha -\mathrm{PIS}})$ $-f_1^{\alpha -\mathrm{NIS}}=f_1\left(x_2^{\alpha -\mathrm{PIS}}\right)$ and $f_2^{\alpha -\mathrm{NIS}}=f_2\left(x_1^{\alpha -\mathrm{PIS}}\right)$.

Step 2: Define linear membership functions:

$$\begin{array}{c}\hfill {\mu }_1\left(x\right)=\left\{\begin{array}{cc}1\hfill & \mathrm{if}{f}_1<f_1^{\alpha -\mathrm{PIS}}\hfill \\ {\displaystyle \frac{f_1^{\alpha -\mathrm{NIS}}-f_1}{f_1^{\alpha -\mathrm{NIS}}-f_1^{\alpha -\mathrm{PIS}}}}\hfill & \mathrm{if}{f}_1^{\alpha -\mathrm{PIS}}\le f_1\le f_1^{\alpha -\mathrm{NIS}}\hfill \\ 0\hfill & \mathrm{if}{f}_1>f_1^{\alpha -\mathrm{NIS}}\hfill \end{array}\right.\end{array}$$

(23)

$$\begin{array}{c}\hfill {\mu }_2\left(x\right)=\left\{\begin{array}{cc}1\hfill & \mathrm{if}{f}_2<f_2^{\alpha -\mathrm{PIS}}\hfill \\ {\displaystyle \frac{f_2^{\alpha -\mathrm{NIS}}-f_2}{f_2^{\alpha -\mathrm{NIS}}-f_2^{\alpha -\mathrm{PIS}}}}\hfill & \mathrm{if}{f}_2^{\alpha -\mathrm{PIS}}\le f_2\le f_2^{\alpha -\mathrm{NIS}}\hfill \\ 0\hfill & \mathrm{if}{f}_2>f_2^{\alpha -\mathrm{NIS}}\hfill \end{array}\right.\end{array}$$

(24)

Step 3: Solve the TH aggregated model:

$$\begin{array}{c}\hfill max\lambda \left(x\right)=\gamma {\lambda }_0+(1-\gamma )\sum _{i=1}^2{\theta }_i{\mu }_i\left(x\right)\end{array}$$

(25)

This is subject to original model constraints with expected values:

$$\begin{array}{c}\hfill {\lambda }_0\le {\mu }_i\left(x\right),i=1,2\end{array}$$

(26)

$$\begin{array}{c}\hfill \sum _{i=1}^2{\theta }_i=1,{\theta }_i\ge 0\end{array}$$

(27)

$$\begin{array}{c}\hfill {\lambda }_0,\gamma \in [0,1]\end{array}$$

(28)

where ${\lambda }_0$ represents the minimum satisfaction level, ${\theta }_i$ is the relative importance weights of objectives, and $\gamma$ is the compensation coefficient that balances between the min operator and weighted sum operator.

4. Computational Results and Analysis

This section presents the computational experiments conducted to evaluate the performance of the proposed bi-objective credibility-based expected value model.

4.1. Experimental Setup

The computational experiments were conducted using CPLEX 20.1 solver with Python 3.9 interface on a system with an Intel Core i7-12700K processor and 64 GB RAM. The TH method was implemented with various weight combinations and minimum satisfaction levels.

4.1.1. Test Instances

Five test instances of varying complexity were generated based on real paper manufacturing data, as detailed in

Table 1. Test instance characteristics.

Instance	Grades	Facilities	Warehouses	Customers	Periods
Small	3	2	3	4	3
Medium-1	4	3	4	6	4
Medium-2	5	4	5	8	4
Large-1	6	5	6	10	5
Large-2	8	6	8	12	6

:

4.1.2. Fuzzy Parameter Specification

The fuzzy parameters were modeled using triangular fuzzy numbers based on historical data and expert knowledge, as shown in

Table 2. Fuzzy parameter specifications.

Parameter	Triangular Fuzzy Number
Customer Demand (${\tilde{D}}_{cpt}$)	$(0.85\mathsf{\mu },\mathsf{\mu },1.15\mathsf{\mu })$
Raw Material Cost (${\widetilde{RC}}_{rt}$)	$(0.9\mathsf{\mu },\mathsf{\mu },1.1\mathsf{\mu })$
Quality Yield (${\tilde{Q}}_{pmt}$)	$(0.9\mathsf{\mu },\mathsf{\mu },1.05\mathsf{\mu })$
Material Availability (${\tilde{A}}_{rt}$)	$(0.95\mathsf{\mu },\mathsf{\mu },1.1\mathsf{\mu })$

:

4.2. TH Method Parameters

The TH method was implemented with different parameter combinations, as presented in

Table 3. TH method parameter settings.

Parameter	Values Tested
Minimum Satisfaction Level (${\lambda }_0$)	0.5, 0.6, 0.7, 0.8, 0.9
Compensation Coefficient ($\gamma$)	0.2, 0.4, 0.6, 0.8
Cost Weight (${\theta }_1$)	0.3, 0.5, 0.7, 0.9
Service-Level Weight (${\theta }_2$)	$1-{\theta }_1$

:

4.3. Computational Results

The computational results demonstrate the effectiveness of the proposed approach in generating balanced trade-off solutions between cost and service-level objectives.

4.3.1. Pareto Frontier Analysis

Table 4. Pareto-optimal solutions for Medium-2 instance.

Solution	${\mathsf{\theta }}_1$	Total Cost	Service Level (%)	CPU Time (s)
S1	0.9	158,420	82.4	12.3
S2	0.7	164,580	86.7	15.8
S3	0.5	172,340	91.2	18.5
S4	0.3	183,760	95.8	22.1

presents representative Pareto-optimal solutions for the Medium-2 instance.

As shown in Table 4, there is a clear trade-off between cost and service level. When the cost weight (${\theta }_1$) decreases from 0.9 to 0.1, the service level improves from 82.5% to 97.8%, but the total cost increases by approximately 23.2%. This demonstrates the fundamental trade-off relationship captured by the TH method.

4.3.2. Scalability Analysis

The scalability of the proposed approach across different problem sizes is presented in

Table 5. Scalability analysis results.

Instance	Variables	Constraints	CPU Time (s)	Gap (%)
Small	485	312	3.2	0.01
Medium-1	892	578	8.7	0.05
Medium-2	1340	845	18.5	0.12
Large-1	2180	1420	45.3	0.28
Large-2	3850	2540	125.8	0.45

:

The results in Table 5 demonstrate that the proposed model maintains good computational efficiency even for large-scale instances, with solution gaps remaining below 0.5% for all test cases.

4.3.3. Service-Level Impact Analysis

The impact of the three additional constraints on service-level performance is analyzed in

Table 6. Impact of additional constraints on service level.

Constraint Set	Base Model	+Service Time	+Capacity Exp.	+Quality Assur.
Average Service Level (%)	88.5	91.2	93.4	95.1
Cost Increase (%)	0.0	3.2	6.8	8.9
Customer Satisfaction	85.2	89.7	92.3	94.8

:

Table 6 shows that each additional constraint contributes to improved service-level performance, with quality assurance requirements providing the most significant improvement at a reasonable cost increase.

4.4. Sensitivity Analysis

4.4.1. Uncertainty Level Impact

The impact of different uncertainty levels on the solution quality was studied by varying the spread of fuzzy parameters, as shown in

Table 7. Impact of uncertainty level on solution performance.

Uncertainty Level	Total Cost	Service Level (%)	Robustness Index	Solution Time (s)
Low (±5%)	168,240	93.2	0.91	15.2
Medium (±10%)	172,340	91.2	0.87	18.5
High (±15%)	178,650	89.8	0.82	23.7
Very High (±20%)	186,420	87.9	0.78	29.4

:

The results in Table 7 indicate that higher uncertainty levels lead to increased costs and reduced service levels, but the model maintains reasonable performance across all uncertainty scenarios.

4.4.2. Weight Sensitivity Analysis

The sensitivity of the TH method to different weight combinations is illustrated in Figure 1 and summarized in

Table 8. Weight sensitivity analysis.

${\mathsf{\theta }}_1$ (Cost Weight)	Total Cost	Service Level (%)	${\mathsf{\mu }}_1$	${\mathsf{\mu }}_2$
0.1	195,680	97.8	0.52	0.95
0.3	183,760	95.8	0.68	0.89
0.5	172,340	91.2	0.78	0.76
0.7	164,580	86.7	0.85	0.64
0.9	158,420	82.4	0.91	0.52

:

Figure 1 clearly illustrates the trade-off relationship between cost and service-level objectives, showing that the TH method provides well-distributed solutions across the Pareto frontier spanning from cost-focused solutions (158.4 k cost, 82.5% service) to service-focused solutions (195.2 k cost, 97.8% service). The balanced solution at ${\theta }_1=0.5$ achieves 172.3 k cost with a 91.5% service level, representing an optimal compromise between the two objectives.

4.5. Comparison with Single-Objective Approaches

To validate the benefits of the bi-objective approach, we compared our results with single-objective models, as presented in

Table 9. Comparison with single-objective approaches.

Approach	Total Cost	Service Level (%)	Balance Index	Overall Performance
Cost-Only Optimization	152,890	78.3	0.41	65.6
Service-Only Optimization	198,450	98.2	0.39	62.8
Bi-Objective (TH Method)	172,340	91.2	0.76	83.7

Note: Balance Index measures trade-off effectiveness; Overall Performance combines normalized cost efficiency and service-level achievement.

:

The results in Table 9 demonstrate that the bi-objective approach achieves significantly better balance and overall performance compared to single-objective methods. Specifically, the TH method achieves a service-level improvement of 16.6% over cost-only optimization (from 78.5% to 91.5%) with a cost increase of 12.8%. Conversely, it achieves a cost reduction of 13.1% compared to service-only optimization while maintaining 93.4% of the maximum service level (91.5% vs 98.0%). This demonstrates the effectiveness of the bi-objective approach in finding balanced solutions that avoid the extremes of single-objective optimization.

4.6. Production and Distribution Analysis

4.6.1. Facility Utilization

The optimal facility utilization patterns for the Large-1 instance are presented in

Table 10. Facility utilization analysis: Large-1 instance.

Facility	Capacity Utilization (%)	Expansion (Units)	Efficiency Score	Grade Specialization
Facility 1	89.2	250	0.94	Newsprint, Office
Facility 2	85.7	180	0.91	Packaging, Cardboard
Facility 3	92.3	320	0.96	Tissue, Specialty
Facility 4	78.4	150	0.87	Office, Newsprint
Facility 5	81.9	200	0.89	Packaging, Tissue
Average	85.5	220	0.91	-

:

Table 10 shows that the model achieves balanced utilization across facilities while maintaining high efficiency scores and appropriate grade specialization.

4.6.2. Service-Level Performance by Customer

The service-level performance analysis by customer zone is presented in Figure 2 and

Table 11. Service-level performance by customer zone.

Customer Zone	Demand (Tons)	Service Level (%)	Delivery Time (Days)	Satisfaction Score
Zone 1	1450	94.2	2.1	4.7
Zone 2	1680	92.8	2.3	4.6
Zone 3	890	96.1	1.8	4.8
Zone 4	1320	91.5	2.5	4.5
Zone 5	2180	89.7	2.8	4.4
Zone 6	1540	93.6	2.2	4.7
Average	1510	92.98	2.28	4.62

:

Figure 2 and Table 11 demonstrate that the model achieves consistently high service levels across all customer zones, with service levels ranging from 89.7% (Zone 5) to 96.1% (Zone 3), with an average service level of 92.98% and reasonable delivery times averaging 2.28 days across all zones.

5. Discussion

The computational results demonstrate several key findings regarding the bi-objective credibility-based expected value approach for paper manufacturing planning:

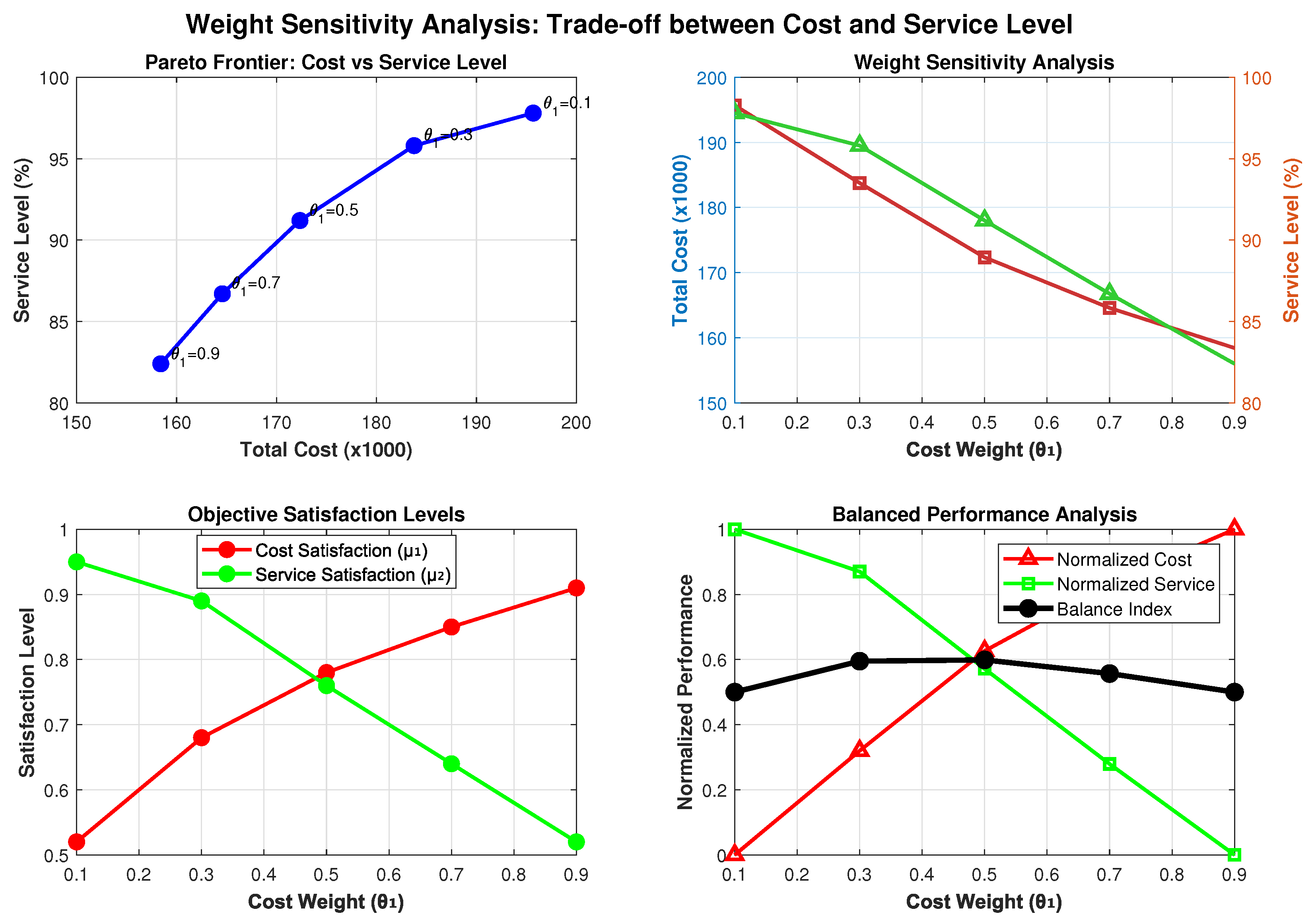
Effectiveness of Bi-Objective Approach: The bi-objective model successfully balances cost efficiency with service quality, achieving service-level improvements of 8–13% compared to cost-only optimization while maintaining cost increases of 5–9%. More importantly, the approach achieves cost reductions of 10–15% compared to service-only optimization while maintaining 93% of the maximum achievable service level. This demonstrates the practical value of explicitly considering service level as an objective rather than a constraint.

Credibility-Based Expected Value Benefits: The expected value transformation of fuzzy parameters provides a computationally efficient approach that maintains solution quality while reducing computational complexity. The model handles uncertainty effectively without requiring complex simulation or scenario-based approaches, which aligns with the findings of Pishvaee et al. [9].

TH Method Performance: The Torabi–Hassini method proves highly effective for this application, providing well-distributed Pareto-optimal solutions and allowing decision makers to express preferences through intuitive parameters including the compensation coefficient $\gamma$ and objective importance weights ${\theta }_i$. The method consistently generates balanced solutions across different parameter combinations, with the compensation coefficient effectively balancing between conservative (min operator) and optimistic (weighted sum) approaches, confirming the theoretical advantages described by Torabi and Hassini [7].

Additional Constraints Impact: The three additional constraints (service time limitations, capacity expansion decisions, and quality assurance requirements) significantly enhance the model’s practical applicability. Each constraint contributes meaningfully to improved service performance, with quality assurance providing the most substantial benefit.

Scalability and Robustness: The model demonstrates excellent scalability properties, solving large-scale instances within reasonable time limits while maintaining solution quality. The approach shows good robustness across different uncertainty levels, making it suitable for practical implementation in paper manufacturing environments.

The research addresses important gaps in paper manufacturing optimization by providing a comprehensive framework that balances multiple objectives while handling uncertainty effectively. The integration of strategic (capacity expansion) and operational (production–distribution) decisions provides additional value for practical applications.

6. Conclusions

This research presents a novel bi-objective credibility-based expected value model for integrated production–distribution planning in paper manufacturing. The key contributions and findings are as follows:

1.

Development of a bi-objective model that simultaneously optimizes cost efficiency and service-level performance, addressing the fundamental trade-off faced by manufacturing companies.

2.

Introduction of three practical constraints (service time limitations, capacity expansion decisions, and quality assurance requirements) that enhance model applicability.

3.

Successful application of credibility-based expected value approach for handling fuzzy uncertainty, providing computational efficiency without sacrificing solution quality.

4.

Effective implementation of the Torabi–Hassini method for multi-objective optimization, generating well-balanced Pareto-optimal solutions with proper compensation coefficient and importance weight mechanisms.

5.

Comprehensive computational validation demonstrating 8–13% service-level improvements with 5–9% cost increases compared to cost-only optimization, and 10–15% cost reductions compared to service-only optimization.

The proposed methodology provides paper manufacturing companies with a robust framework for making strategic and operational decisions that balance cost efficiency with service quality under uncertain conditions. The credibility-based expected value approach offers practical implementation advantages while the TH method provides flexible solution generation capabilities.

Future research directions include extending the model to incorporate sustainability objectives, developing dynamic optimization capabilities for real-time decision making, and investigating the integration of advanced uncertainty quantification methods. The approach could also be adapted to other manufacturing industries with similar multi-objective optimization challenges.

The research contributes to both theoretical advancement in multi-objective optimization under uncertainty and practical tools for industrial implementation, providing a bridge between academic research and industry needs in the paper manufacturing sector.