Adaptive Observer-Based Robust Control of Mismatched Buck DC–DC Converters for Renewable Energy Applications †
Abstract
1. Introduction
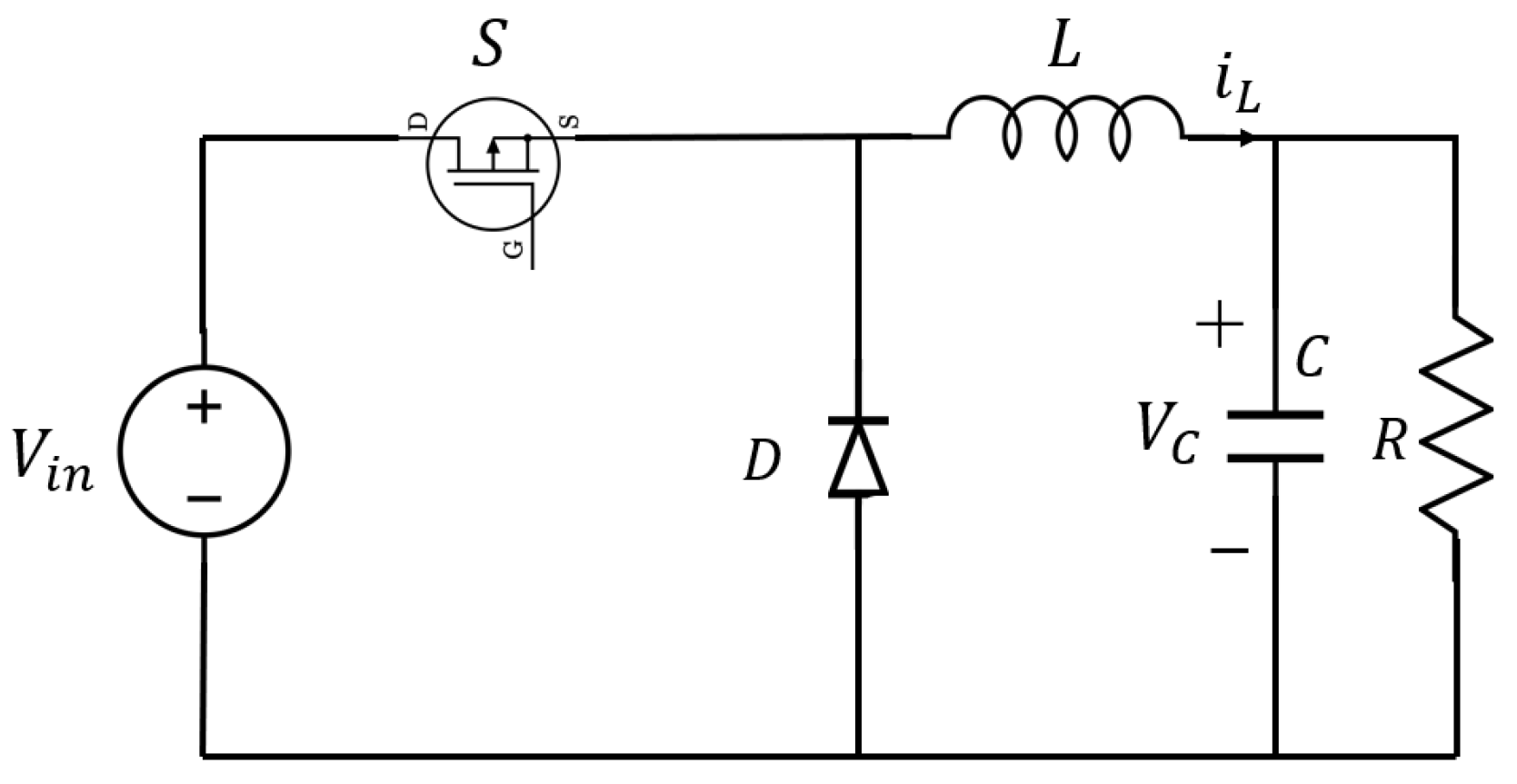
2. Description of Buck DC–DC Converter
- , , , .
3. Control Design
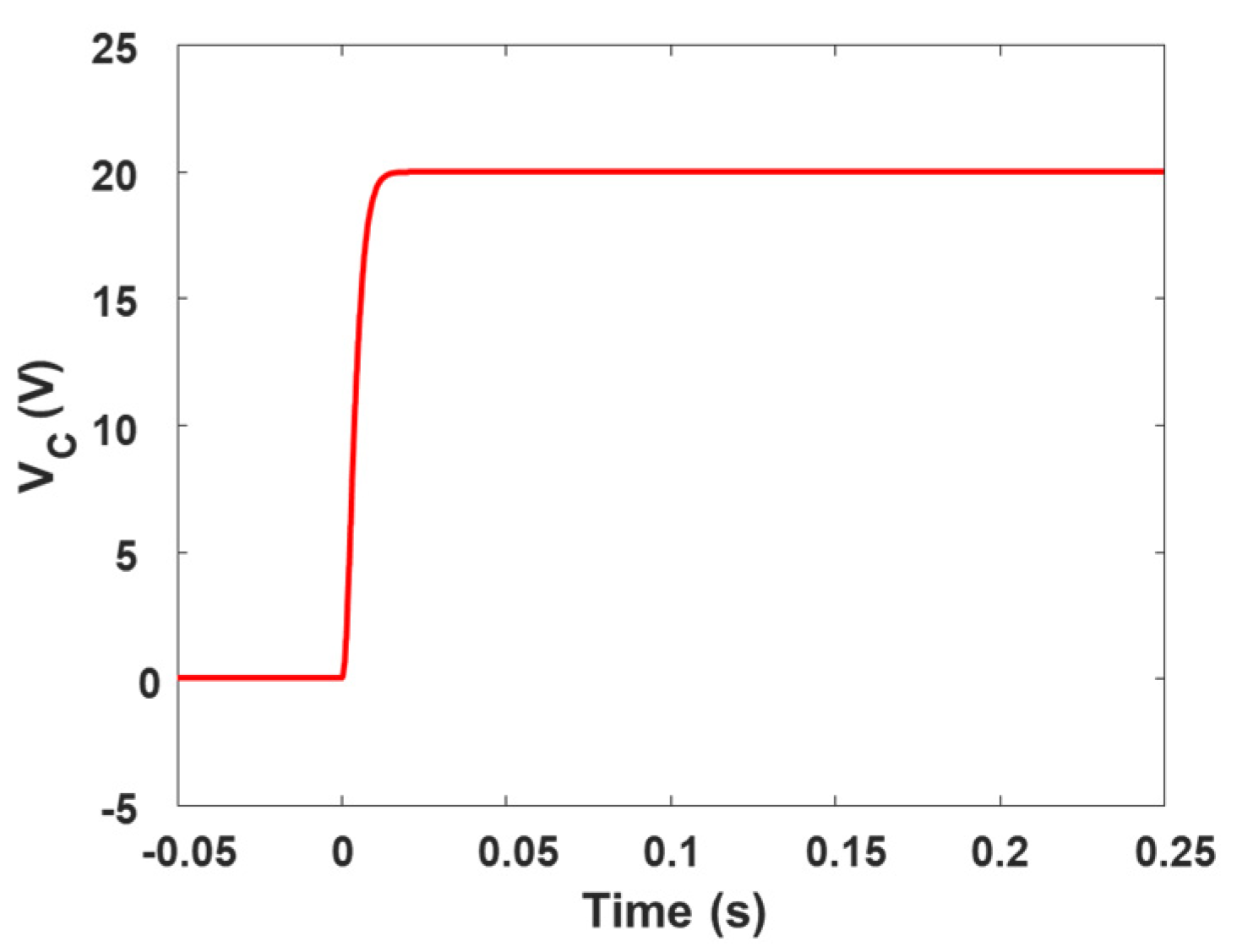
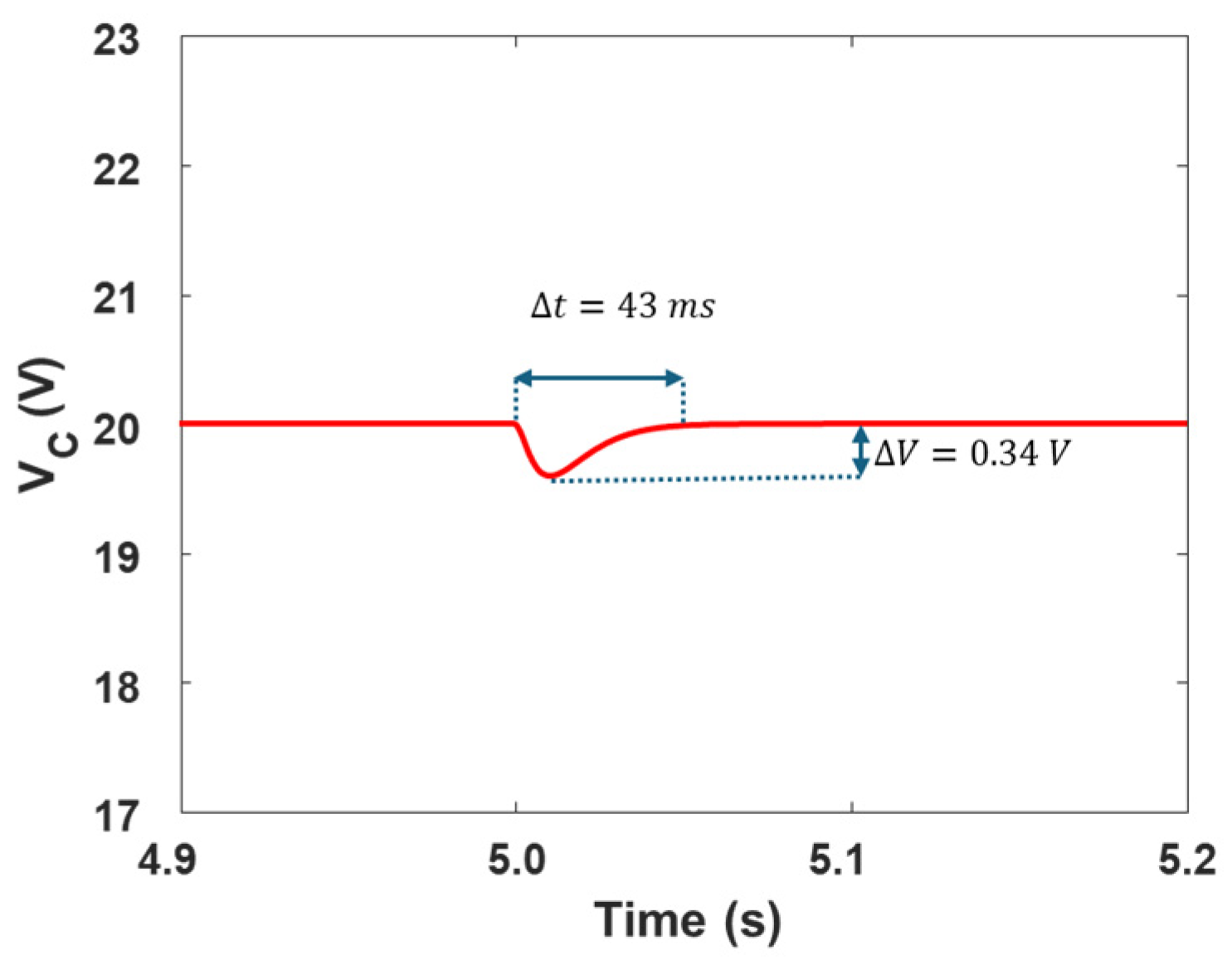
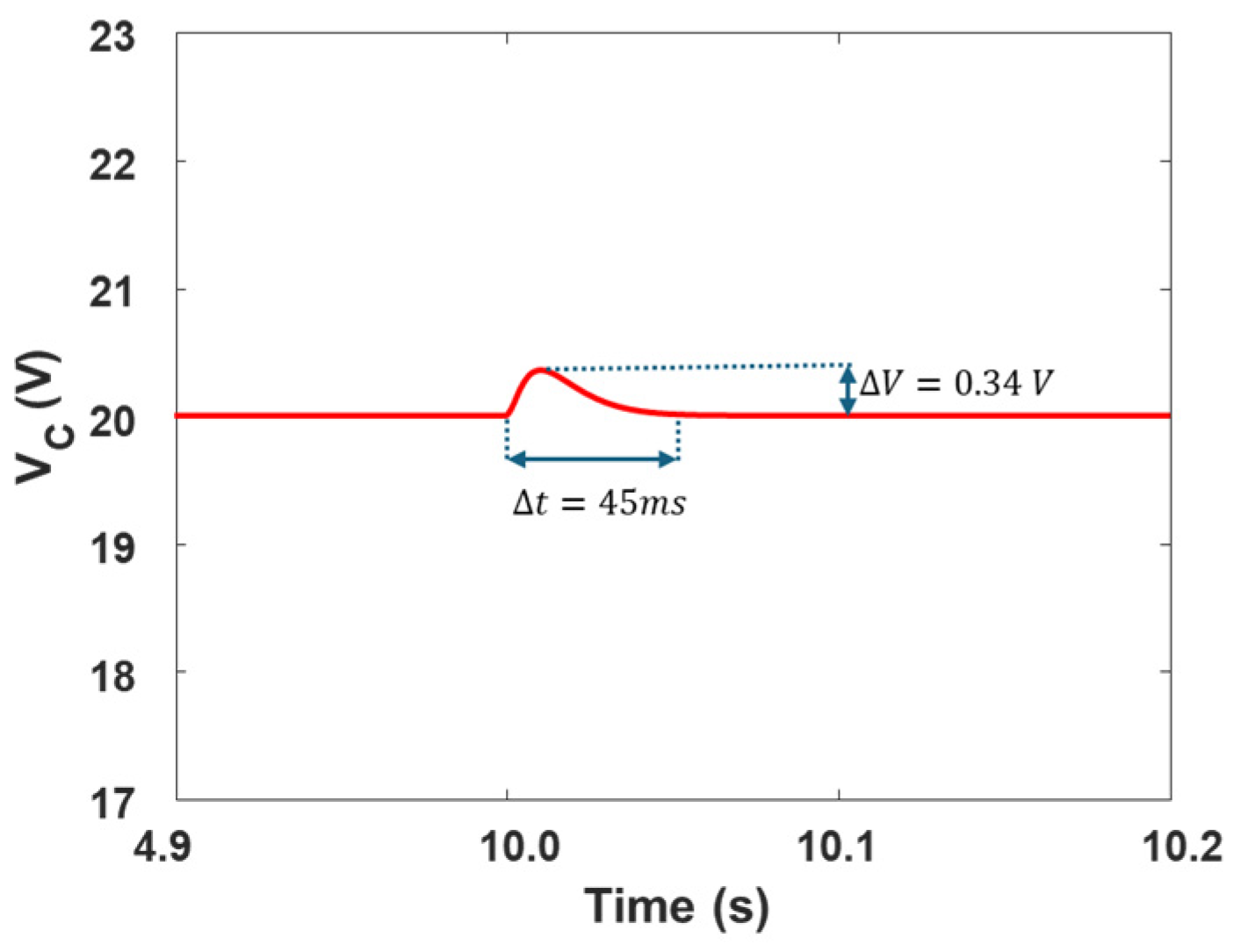
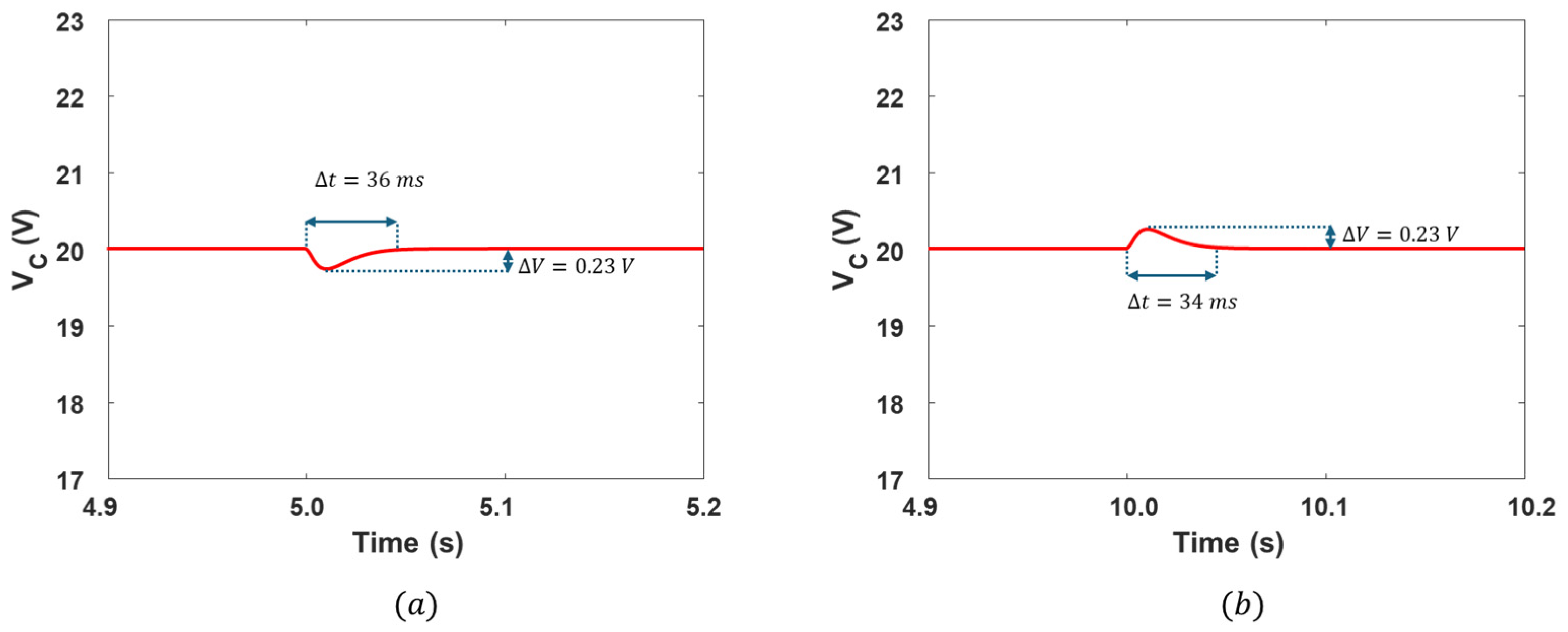
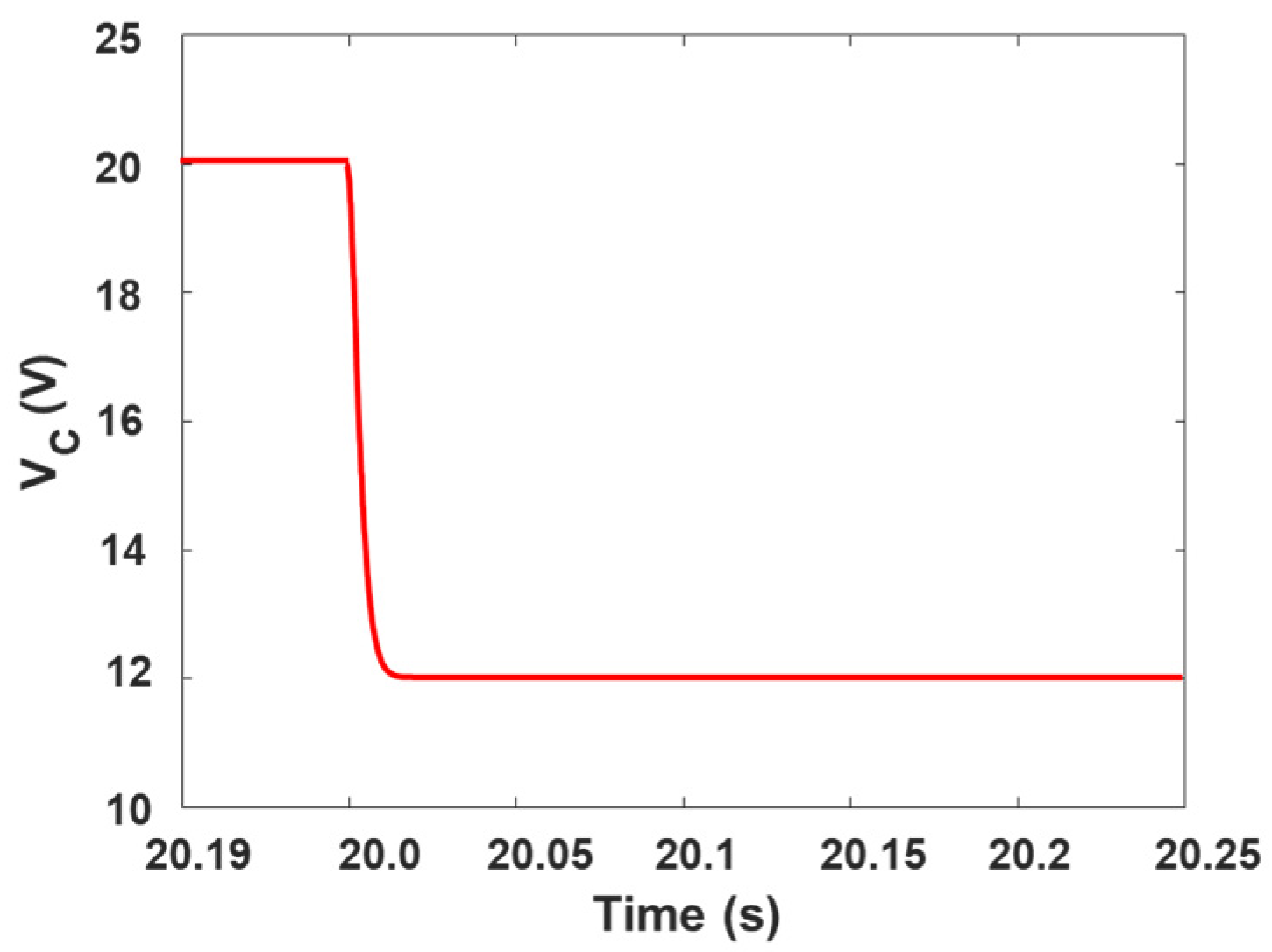
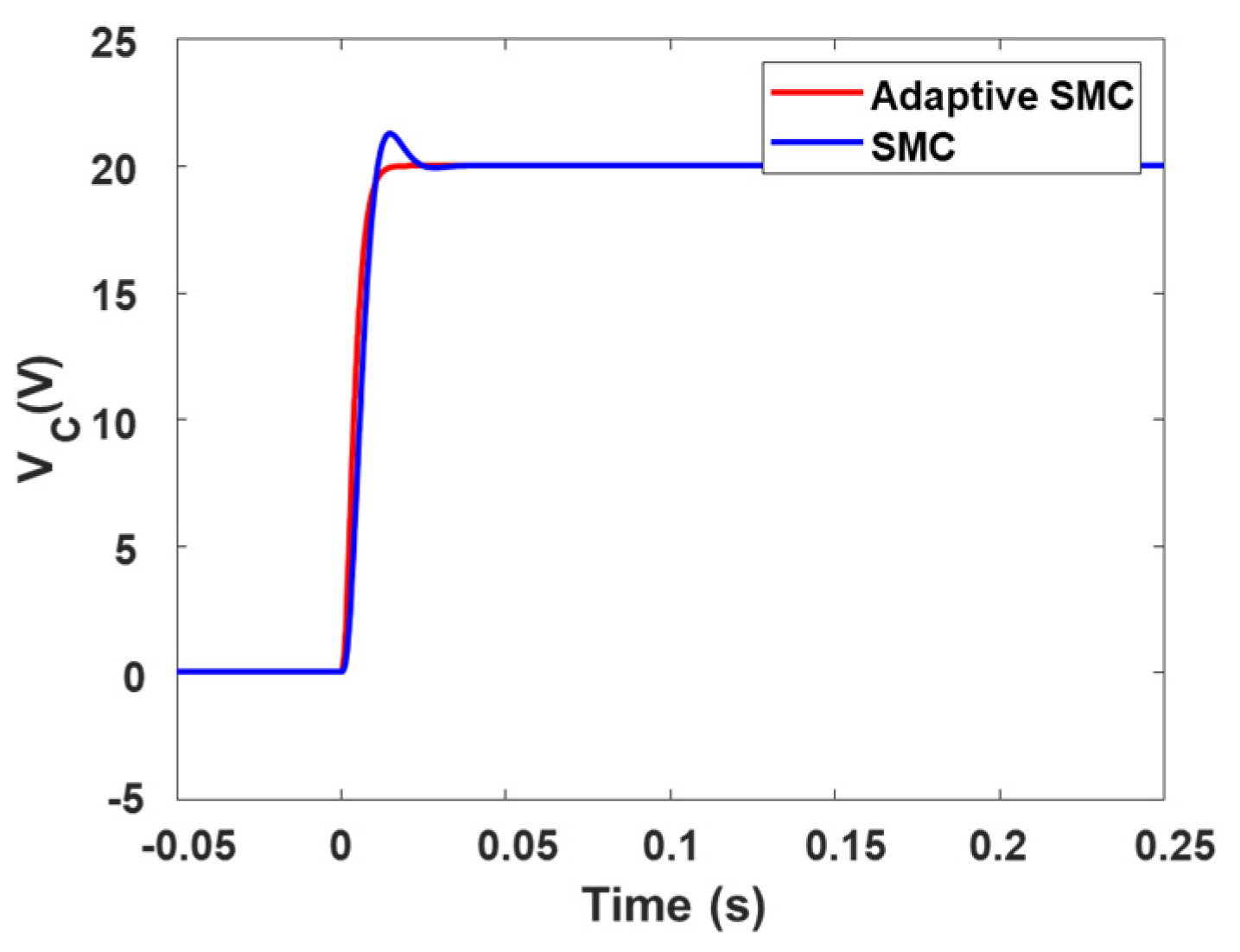
4. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ibarra, E.; Arias, A.; de Alegría, I.M.; Otero, A.; De Mallac, L. Digital control of multiphase series capacitor buck converter prototype for the powering of HL-LHC inner triplet magnets. IEEE Trans. Ind. Electron. 2021, 69, 10014–10024. [Google Scholar] [CrossRef]
- Babes, B.; Mekhilef, S.; Boutaghane, A.; Rahmani, L. Fuzzy approximation-based fractional-order nonsingular terminal sliding mode controller for DC–DC buck converters. IEEE Trans. Power Electron. 2021, 37, 2749–2760. [Google Scholar] [CrossRef]
- Zad, H.S.; Ulasyar, A.; Zohaib, A.; Irfan, M.; Yaqoob, Z.; Haider, S.A. Robust & Optimal Predictive Current Control for Bi-Directional DC-DC Converter in Distributed Energy Storage Systems. Eng. Proc. 2024, 75, 26. [Google Scholar]
- Malge, S.V.; Patil, S.L.; Deshpande, A.S.; Aher, P.K. Mismatched Disturbance Estimation Based Sliding Mode Control of DC-DC Power Converter. In Proceedings of the 2nd International Conference on Intelligent Technologies (CONIT), Karnataka, India, 24–26 June 2022. [Google Scholar]
- Zad, H.S.; Ulasyar, A.; Zohaib, A. Adaptive Observer Based Output Voltage-Tracking Control of DC-DC Boost Converters. In Proceedings of the 21st International Bhurban Conference on Applied Sciences and Technology (IBCAST), Islamabad, Pakistan, 20–23 August 2024; pp. 584–588. [Google Scholar]
- Alshalalfah, A.L.; Hamad, G.B.; Mohamed, O.A. Towards safe and robust closed-loop artificial pancreas using improved PID-based control strategies. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 3147–3157. [Google Scholar] [CrossRef]
- Sheh Zad, H.; Ulasyar, A.; Zohaib, A.; Khattak, A. Adaptive sliding mode predictive power control of three-phase AC/DC converters. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2022, 236, 897–912. [Google Scholar] [CrossRef]
- Liu, Z.; Lin, X.; Gao, Y.; Xu, R.; Wang, J.; Wang, Y.; Liu, J. Fixed-time sliding mode control for DC/DC buck converters with mismatched uncertainties. IEEE Trans. Circuits Syst. I Regul. Pap. 2022, 70, 472–480. [Google Scholar] [CrossRef]
- Qin, C.; Zhang, Z.; Fang, Q. Adaptive backstepping fast terminal sliding mode control with estimated inverse hysteresis compensation for piezoelectric positioning stages. IEEE Trans. Circuits Syst. II Express Briefs 2023, 71, 1186–1190. [Google Scholar] [CrossRef]
- Fan, D.; Zhang, X.; Pan, W. Sliding mode control for strict-feedback nonlinear impulsive systems with matched disturbances. IEEE Trans. Circuits Syst. II Express Briefs 2023, 71, 787–791. [Google Scholar] [CrossRef]
- Zad, H.S.; Ulasyar, A.; Zohaib, A.; Irfan, M.; Haider, S.A.; Yaqoob, Z. Adaptive Sliding Mode Control of DC–DC Buck Converter with Load Fluctuations for Renewable Energy Systems. Eng. Proc. 2024, 75, 10. [Google Scholar]
- Zhang, P.; Kao, Y.; Hu, J.; Niu, B.; Xia, H.; Wang, C. Finite-time observer-based sliding-mode control for Markovian jump systems with switching chain: Average dwell-time method. IEEE Trans. Cybern. 2021, 53, 248–261. [Google Scholar] [CrossRef] [PubMed]
- Dong, S.; Liu, M.; Wu, Z.G.; Shi, K. Observer-based sliding mode control for Markov jump systems with actuator failures and asynchronous modes. IEEE Trans. Circuits Syst. II Express Briefs 2020, 68, 1967–1971. [Google Scholar] [CrossRef]
- Zhang, H.; Yan, Y.; Mu, Y.; Ming, Z. Neural network-based adaptive sliding-mode control for fractional order fuzzy system with unmatched disturbances and time-varying delays. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 5174–5184. [Google Scholar] [CrossRef]
- Zhen, S.; Yaen, X.; Chengchen, D.; Kun, Z.; Yushan, H.; Yong, H. Disturbance observer based finite-time coordinated attitude tracking control for spacecraft on SO3. J. Syst. Eng. Electron. 2020, 31, 1274–1285. [Google Scholar] [CrossRef]
| Description | Parameter | Value |
|---|---|---|
| Reference Voltage | 20→15 V | |
| Input Voltage | 30 V | |
| Filter Inductor | 1.5 mH | |
| Load Resistance | 10→20 | |
| Filter Capacitor | 2200 F |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zad, H.S.; Ulasyar, A.; Zohaib, A.; Khalid, S. Adaptive Observer-Based Robust Control of Mismatched Buck DC–DC Converters for Renewable Energy Applications. Eng. Proc. 2025, 111, 22. https://doi.org/10.3390/engproc2025111022
Zad HS, Ulasyar A, Zohaib A, Khalid S. Adaptive Observer-Based Robust Control of Mismatched Buck DC–DC Converters for Renewable Energy Applications. Engineering Proceedings. 2025; 111(1):22. https://doi.org/10.3390/engproc2025111022
Chicago/Turabian StyleZad, Haris Sheh, Abasin Ulasyar, Adil Zohaib, and Sohail Khalid. 2025. "Adaptive Observer-Based Robust Control of Mismatched Buck DC–DC Converters for Renewable Energy Applications" Engineering Proceedings 111, no. 1: 22. https://doi.org/10.3390/engproc2025111022
APA StyleZad, H. S., Ulasyar, A., Zohaib, A., & Khalid, S. (2025). Adaptive Observer-Based Robust Control of Mismatched Buck DC–DC Converters for Renewable Energy Applications. Engineering Proceedings, 111(1), 22. https://doi.org/10.3390/engproc2025111022






