Developing a Multi-Criteria Decision-Making (MCDM) Approach for Selecting Educational Collaborative Robots (CoBots) in West African Countries †
Abstract
1. Introduction
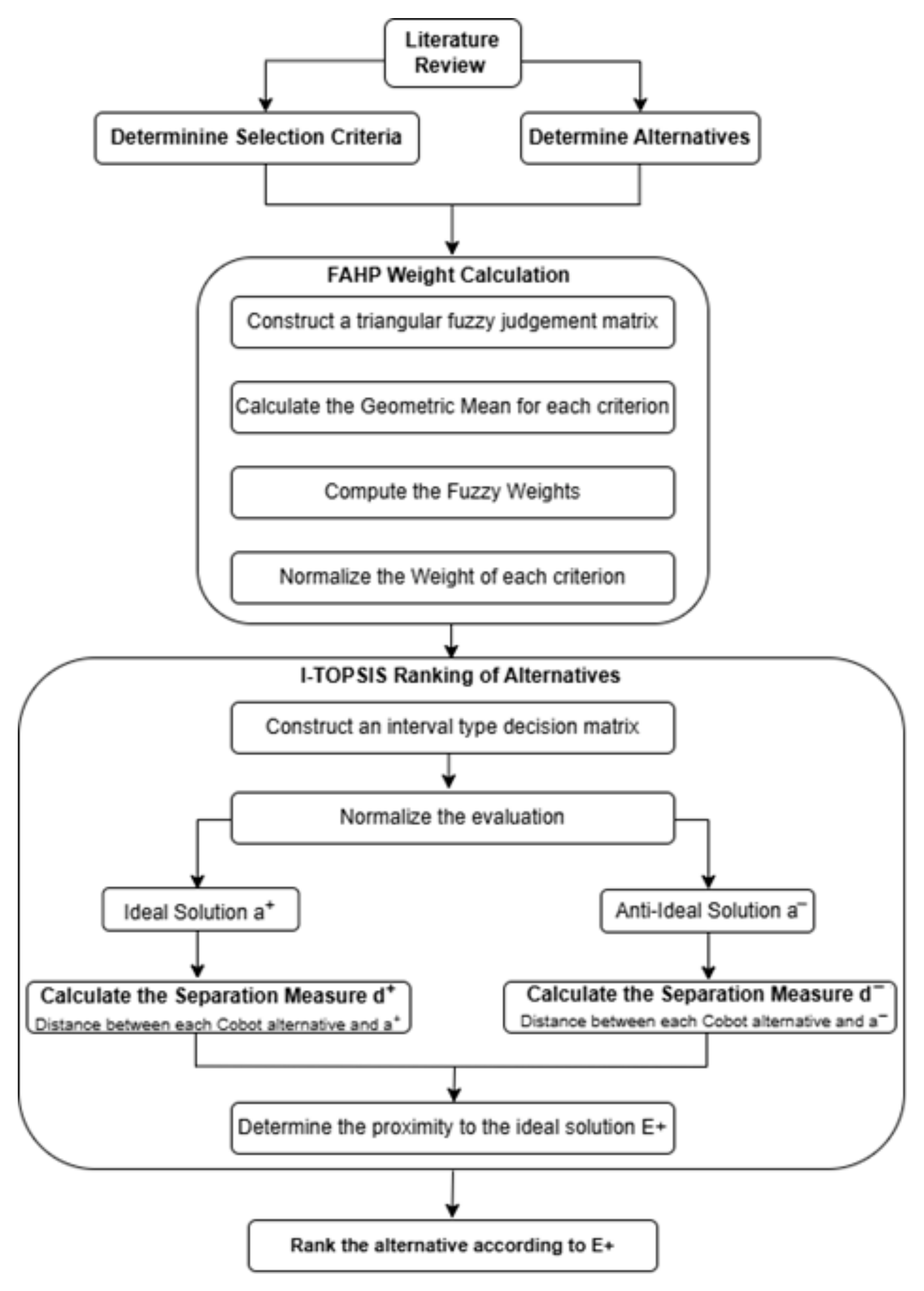
2. Methodology
Computational Steps
- 1.
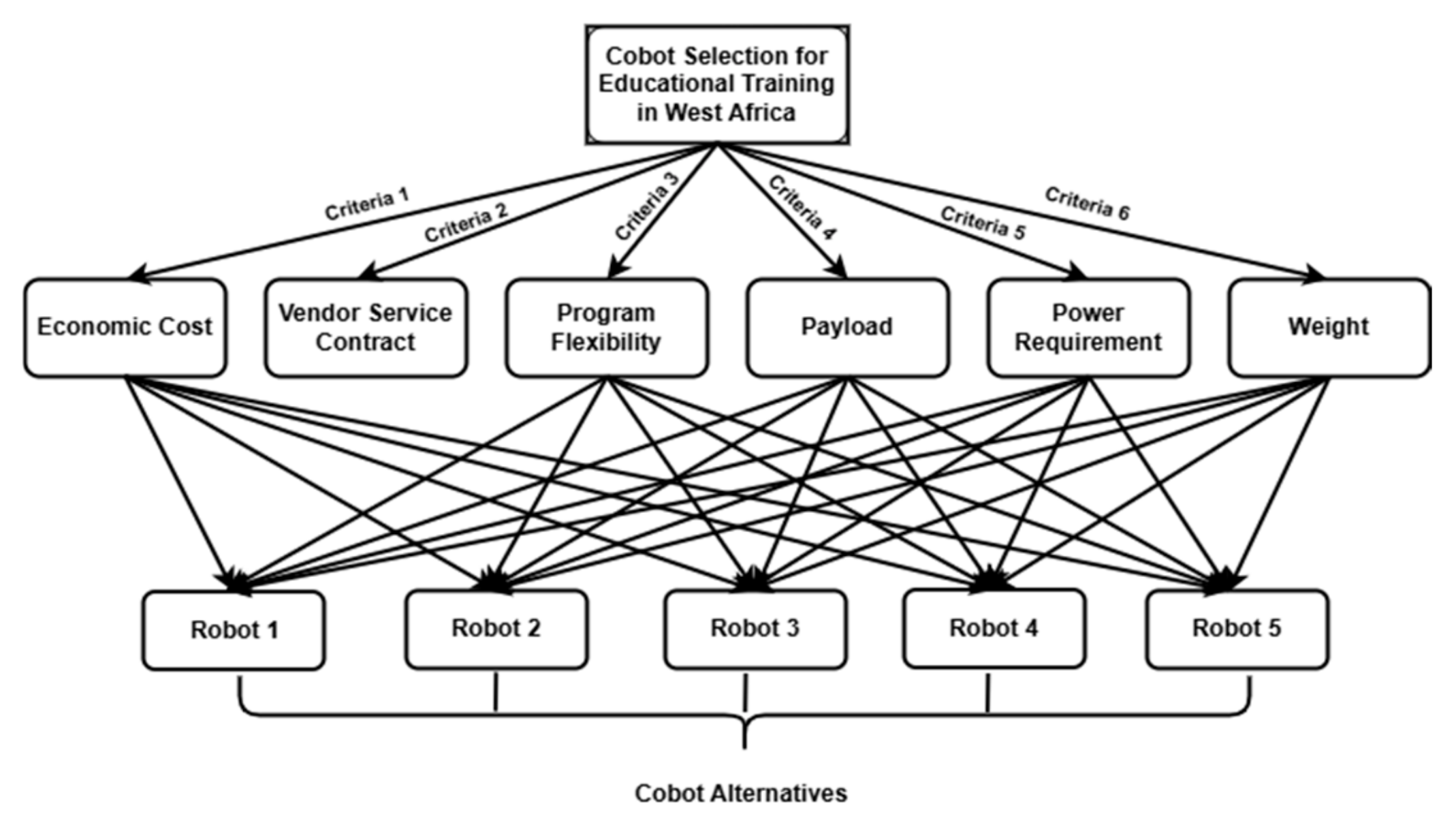
- Determination of critical factors: Some factors were identified from the literature review and information about Africa. Similar criteria were merged to yield 6, as shown in Table 1.
- 2.
- Determination of alternatives: CoBot alternatives and their relevant criteria in this work were obtained from an online search for the best CoBots used for robot education, works of literature about CoBots, emails, and past quotations for robot purchases from some companies. However, the CoBot names were hidden during the survey to avoid biases.
- 3.
- FAHP
- i.
- Expert judgment was set to be collected via audio interviews, self-recorded responses, or Google Sheets, using the linguistic variables shown in Table 2.
- ii.
- The pairwise comparison matrix resembles the one shown in Equation (1), where denotes the importance of factor i compared to factor j.
- iii.
- Consistency Ratio (CR) calculation
- iv.
- Determining the Geometric Mean for each criterion
- v.
- Defuzzify to obtain the non-fuzzified weight for the criterion.
- vi.
- The normalized weight of each criterion is computed using the formula:
- vii.
- Aggregate assessment—This is calculated for each variant by multiplying the normalized weights of the criteria and variants.
- viii.
- The variant with the highest aggregate is selected as the best, as it reflects the average preferences of the decision-makers. However, since we are continuing with I-TOPSIS, this step is skipped.
- 4.
- I-TOPSIS
- i.
- Decision Matrix
- ii.
- Determine the positive and negative ideal solutions as shown below:
- iii.
- Compute the separation measures between the given evaluations X = , calculating , denoted as respectively, using Equation (9), where weight , obtained from the FAHP, is used:
- iv.
- Calculate the relative proximity coefficient (.
3. Experiment and Results
3.1. Case Study
3.2. Results and Analysis
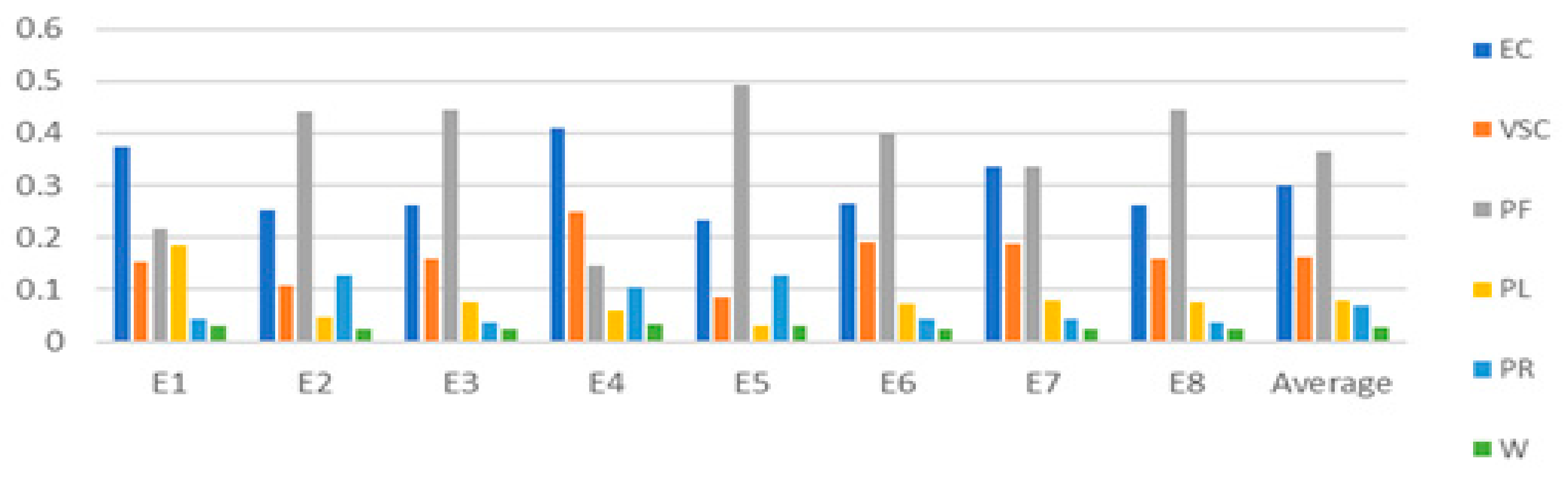
3.2.1. FAHP
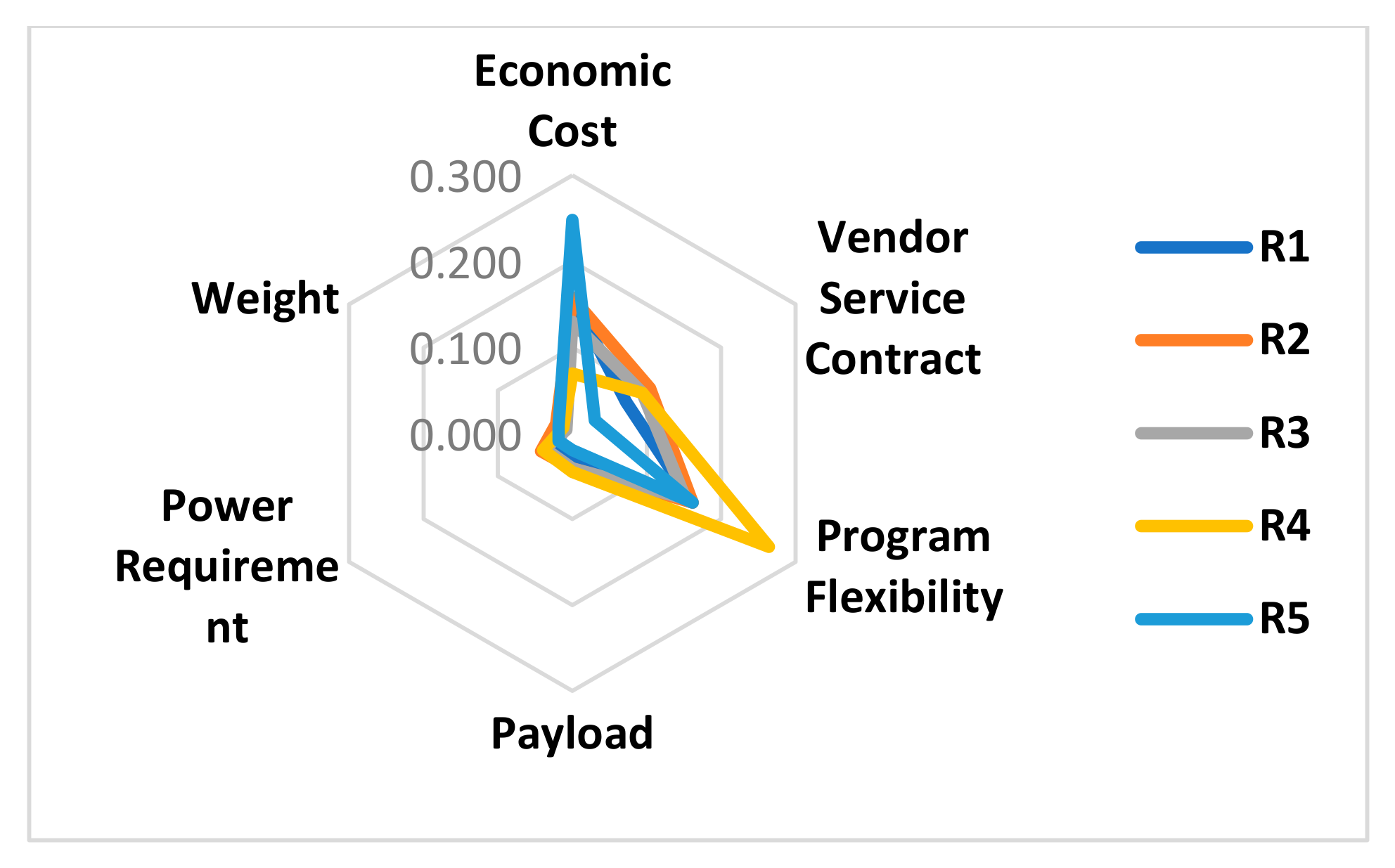
Interpretation of Final Weights
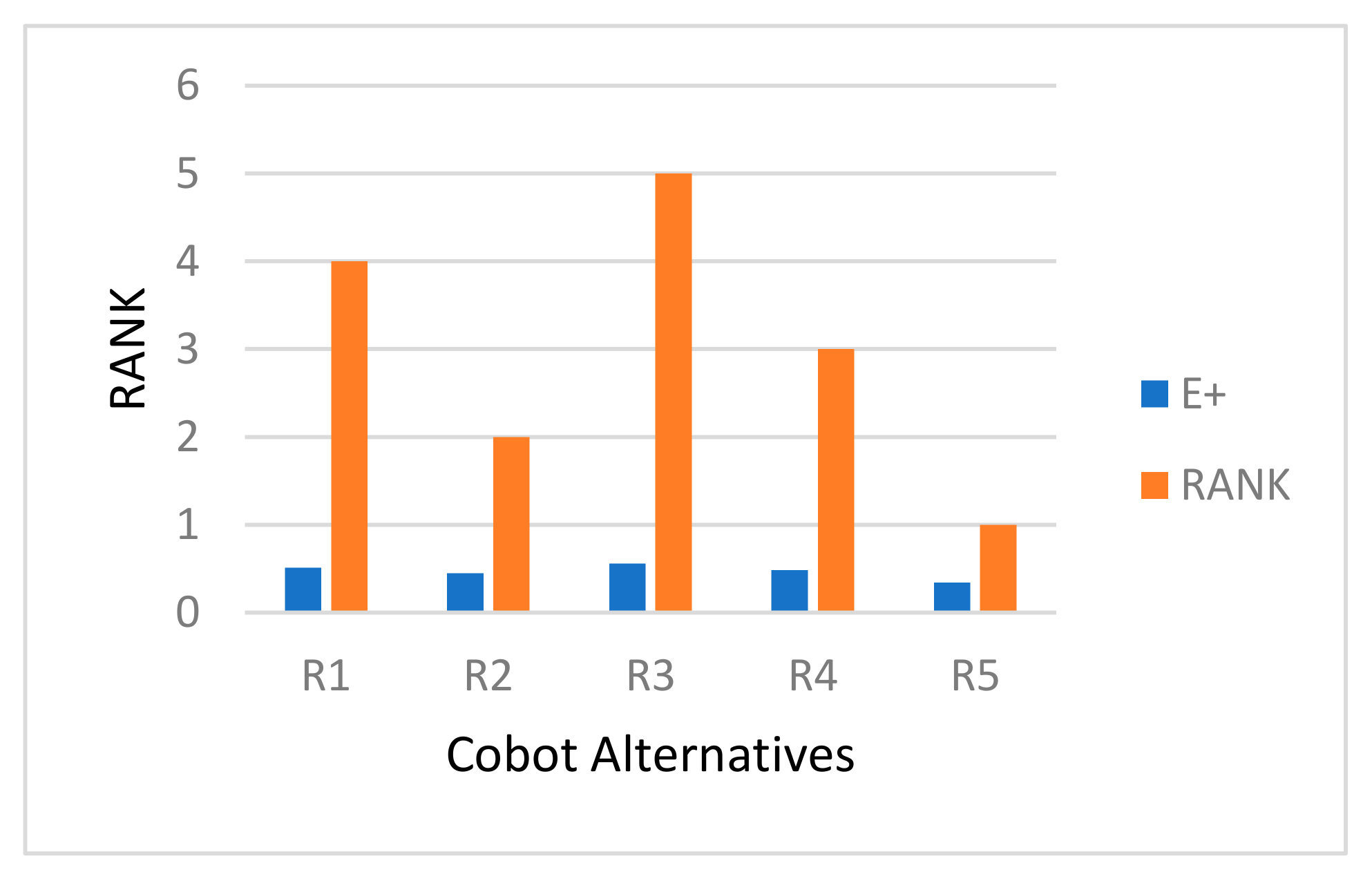
3.2.2. I-TOPSIS
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bui, H.-A.; Nguyen, X.-T. A novel multicriteria decision-making process for selecting spot welding robot with removal effects of criteria techniques. Int. J. Interact. Des. Manuf. (IJIDeM) 2024, 18, 1033–1052. [Google Scholar] [CrossRef]
- Evripidou, S.; Doitsidis, L.; Tsinarakis, G.; Zinonos, Z.; Chatzichristofis, S.A. Selecting a robotic platform for education. In Proceedings of the 2022 IEEE International Conference On Consumer Electronics (ICCE), Las Vegas, NV, USA, 7–9 January 2022; pp. 1–6. [Google Scholar]
- Parameshwaran, R.; Kumar, S.P.; Saravanakumar, K. An integrated fuzzy MCDM based approach for robot selection considering objective and subjective criteria. Appl. Soft Comput. 2015, 26, 31–41. [Google Scholar] [CrossRef]
- Garg, H.; Sharaf, I.M. A new spherical aggregation function with the concept of spherical fuzzy difference for spherical fuzzy EDAS and its application to industrial robot selection. Comput. Appl. Math. 2022, 41, 212. [Google Scholar] [CrossRef]
- Mouhib, H.; Amar, S.; Elrhanimi, S.; El Abbadi, L. Maximizing efficiency and collaboration: Comparing Robots and Cobots in the Automotive Industry–A Multi-Criteria Evaluation Approach. Int. J. Ind. Eng. Manag. 2024, 15, 238–253. [Google Scholar] [CrossRef]
- AUC/OECD. Africa’s Development Dynamics 2021: Digital Transformation for Quality Jobs; OECD Publishing: France, Paris, 2021. [Google Scholar] [CrossRef]
- Chatterjee, S.; Das, P.P.; Chakraborty, S. An LOPCOW-OPTBIAS-based integrated approach for cobot selection in manufacturing assembly operations. Int. J. Multicriteria Decis. Mak. 2024, 10, 47–69. [Google Scholar] [CrossRef]
- Veza, I.; Mladineo, M.; Kutlesa, M.; Gjeldum, N.; Bilic, B.; Crnjac Zizic, M.; Aljinovic, A.; Basic, A. Selection of the cobot workstation for the learning factory by using the multi-criteria analysis. In Proceedings of the 12th Conference on Learning Factories (CLF 2022), Singapore, 11–13 April 2022. [Google Scholar]
- Ojokoh, B.; Afolayan, A. Analysis of Multi-Criteria Decision Making Methods for Contractor Selection in Nigeria. In Proceedings of the 5th Covenant University Conference on E-Governance in Nigeria (CUCEN 2018), Ota Ogun, Nigeria, 6–8 June 2018. [Google Scholar]
- Sivalingam, C.; Subramaniam, S.K. Cobot selection using hybrid AHP-TOPSIS based multi-criteria decision making technique for fuel filter assembly process. Heliyon 2024, 10, e26374. [Google Scholar]
- Kong, H.-Q.; Zhang, N. Risk assessment of water inrush accident during tunnel construction based on FAHP-I-TOPSIS. J. Clean. Prod. 2024, 449, 141744. [Google Scholar] [CrossRef]
- Mahanta, G.B.; Mohanty, B.; Rout, A.; Biswal, B.B.; Jha, A. Selection of cobot for human-robot collaboration for robotic assembly task with Best Worst MCDM techniques. In Proceedings of the 2023 IEEE 7th Conference on Information and Communication Technology (CICT), Jabalpur, India, 15–17 December 2023; pp. 1–6. [Google Scholar]
- Vahdani, B.; Mousavi, S.M.; Tavakkoli-Moghaddam, R.; Ghodratnama, A.; Mohammadi, M. Robot selection by a multiple criteria complex proportional assessment method under an interval-valued fuzzy environment. Int. J. Adv. Manuf. Technol. 2014, 73, 687–697. [Google Scholar] [CrossRef]
- Gitinavard, H.; Mousavi, S.M.; Vahdani, B. Soft computing-based new interval-valued hesitant fuzzy multi-criteria group assessment method with last aggregation to industrial decision problems. Soft Comput. 2017, 21, 3247–3265. [Google Scholar] [CrossRef]
- Petrov, I. Multi-criteria selection of industrial robots: Modelling users’ preferences in combined AHP-Entropy-TOPSIS. In Proceedings of the 2022 5th International Conference on Computing and Informatics (ICCI), New Cairo, Cairo, Egypt, 9–10 March 2022; pp. 126–131. [Google Scholar]
- Liu, H.-C.; Ren, M.-L.; Wu, J.; Lin, Q.-L. An interval 2-tuple linguistic MCDM method for robot evaluation and selection. Int. J. Prod. Res. 2014, 52, 2867–2880. [Google Scholar] [CrossRef]
- Sen, D.K.; Datta, S.; Mahapatra, S.S. Extension of TODIM for decision making in fuzzy environment: A case empirical research on selection of industrial robot. Int. J. Serv. Oper. Manag. 2017, 26, 238–276. [Google Scholar] [CrossRef]
- Hong Son, N.; Hieu, T.T. Selection of Welding Robot by Multi-Criteria Decisionmaking Method. East.-Eur. J. Enterp. Technol. 2023, 1, 66–72. [Google Scholar]
- Chodha, V.; Dubey, R.; Kumar, R.; Singh, S.; Kaur, S. Selection of industrial arc welding robot with TOPSIS and Entropy MCDM techniques. Mater. Today Proc. 2022, 50, 709–715. [Google Scholar] [CrossRef]
- Garg, C.P.; Görçün, Ö.F.; Kundu, P.; Küçükönder, H. An integrated fuzzy MCDM approach based on Bonferroni functions for selection and evaluation of industrial robots for the automobile manufacturing industry. Expert Syst. Appl. 2023, 213, 118863. [Google Scholar] [CrossRef]
- Suszyński, M.; Rogalewicz, M. Selection of an industrial robot for assembly jobs using multi-criteria decision making methods. Manag. Prod. Eng. Rev. 2020, 11, 62–72. [Google Scholar] [CrossRef]
| S/N | CRITICAL FACTOR/CRITERION | REFERENCE |
|---|---|---|
| 1 4 | [12,13] | |
| 2 6 | [14,15] | |
| 3 | Vendor’s Service Contract | [16,17] |
| 4 | Power Requirement | [14,18] |
| 5 | Payload | [19,20] |
| 6 | Weight | [10,21] |
| Simple Fuzzy No. | Scale | Linguistic Terms |
|---|---|---|
| 9 | (9, 9, 9) | Extremely More Important |
| 7 | (6, 7, 8) | Very Strongly More Important |
| 5 | (4, 5, 6) | Strongly More Important |
| 3 | (2, 3, 4) | Moderately More Important |
| 1 | (1, 1, 1) | Equally Important |
| 1/3 | (1/4, 1/3, 1/2) | Moderately Less Important |
| 1/5 | (1/6, 1/5, 1/4) | Strongly Less Important |
| 1/7 | (1/8, 1/7, 1/6) | Very Strongly Less Important |
| 1/9 | (1/9, 1/9, 1/9) | Extremely Less Important |
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| RI | 0 | 0 | 0.52 | 0.89 | 1.12 | 1.26 | 1.36 | 1.41 | 1.46 |
| S/N | SCALE | LINGUISTIC TERMS |
|---|---|---|
| 1 | [0, 2] | Very Poor |
| 2 | [1, 3] | Poor |
| 3 | [2, 4] | Fair |
| 4 | [3, 5] | Good |
| 5 | [4, 6] | Very Good |
| S/N | Position | Method of Collection | Type of Organization |
|---|---|---|---|
| 1 | Professor of Mechatronics (E1) | Google Sheet | Public university in Nigeria |
| 2 | Consultant (E2) | Self-recording | Public–private partnership training center in Nigeria |
| 3 | Engineer I (R&D) (E3) | Google Sheet | Public research institute in Nigeria |
| 4 | Head of Certification (E4) | Google Sheet | National IT regulator in Ghana |
| 5 | Assistant Chief Engineer (R&D) (E5) | Interview | Public research institute in Nigeria |
| 6 | Senior IT Officer (E6) | Self-recording | Public ministry in Ghana |
| 7 | Senior Technologist—Mechatronics (E7) | Self-recording | Public educational institute in Nigeria |
| 8 | Senior Lecturer—Robotics and Computer Education (E8) | Self-recording | Public college of education in Nigeria |
| E1 | E2 | E3 | E4 | E5 | E6 | E7 | E8 | Average | Rank | |
|---|---|---|---|---|---|---|---|---|---|---|
| EC | 0.373 | 0.253 | 0.261 | 0.408 | 0.233 | 0.267 | 0.334 | 0.261 | 0.300 | 2 |
| VSC | 0.152 | 0.108 | 0.158 | 0.250 | 0.086 | 0.191 | 0.188 | 0.158 | 0.161 | 3 |
| PF | 0.216 | 0.442 | 0.444 | 0.145 | 0.494 | 0.401 | 0.334 | 0.444 | 0.365 | 1 |
| PL | 0.184 | 0.047 | 0.075 | 0.061 | 0.030 | 0.074 | 0.079 | 0.075 | 0.078 | 4 |
| PR | 0.043 | 0.126 | 0.038 | 0.103 | 0.127 | 0.045 | 0.042 | 0.038 | 0.070 | 5 |
| W | 0.032 | 0.026 | 0.024 | 0.033 | 0.030 | 0.024 | 0.023 | 0.024 | 0.027 | 6 |
| Cobots | d+ | d− | E+ | Rank |
|---|---|---|---|---|
| R1 | 0.0723 | 0.08 | 0.5102 | 2 |
| R2 | 0.0881 | 0.07 | 0.4504 | 4 |
| R3 | 0.0674 | 0.09 | 0.561 | 1 |
| R4 | 0.099 | 0.09 | 0.4845 | 3 |
| R5 | 0.1315 | 0.07 | 0.344 | 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Umar, D.Y.; Khan, A.; Ahn, Y. Developing a Multi-Criteria Decision-Making (MCDM) Approach for Selecting Educational Collaborative Robots (CoBots) in West African Countries. Eng. Proc. 2025, 111, 18. https://doi.org/10.3390/engproc2025111018
Umar DY, Khan A, Ahn Y. Developing a Multi-Criteria Decision-Making (MCDM) Approach for Selecting Educational Collaborative Robots (CoBots) in West African Countries. Engineering Proceedings. 2025; 111(1):18. https://doi.org/10.3390/engproc2025111018
Chicago/Turabian StyleUmar, Deyire Yusuf, Afrasyab Khan, and Yonghan Ahn. 2025. "Developing a Multi-Criteria Decision-Making (MCDM) Approach for Selecting Educational Collaborative Robots (CoBots) in West African Countries" Engineering Proceedings 111, no. 1: 18. https://doi.org/10.3390/engproc2025111018
APA StyleUmar, D. Y., Khan, A., & Ahn, Y. (2025). Developing a Multi-Criteria Decision-Making (MCDM) Approach for Selecting Educational Collaborative Robots (CoBots) in West African Countries. Engineering Proceedings, 111(1), 18. https://doi.org/10.3390/engproc2025111018






