Extract Temperature Coefficients of LGS for High-Temperature Applications Based on the Finite Element Method †
Abstract
1. Introduction
2. Method
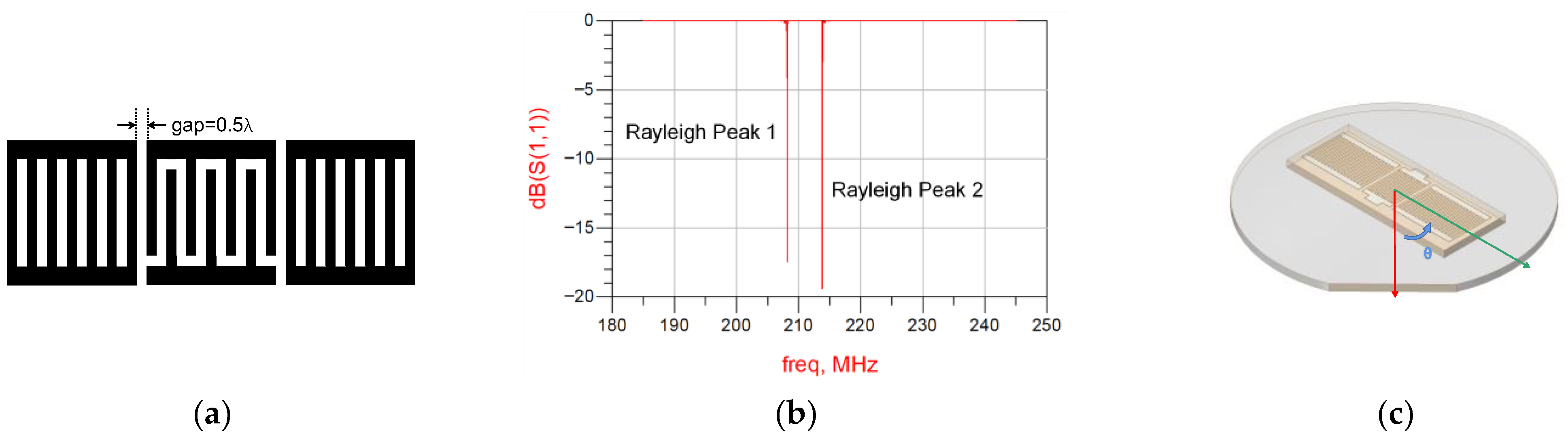
2.1. Device Design
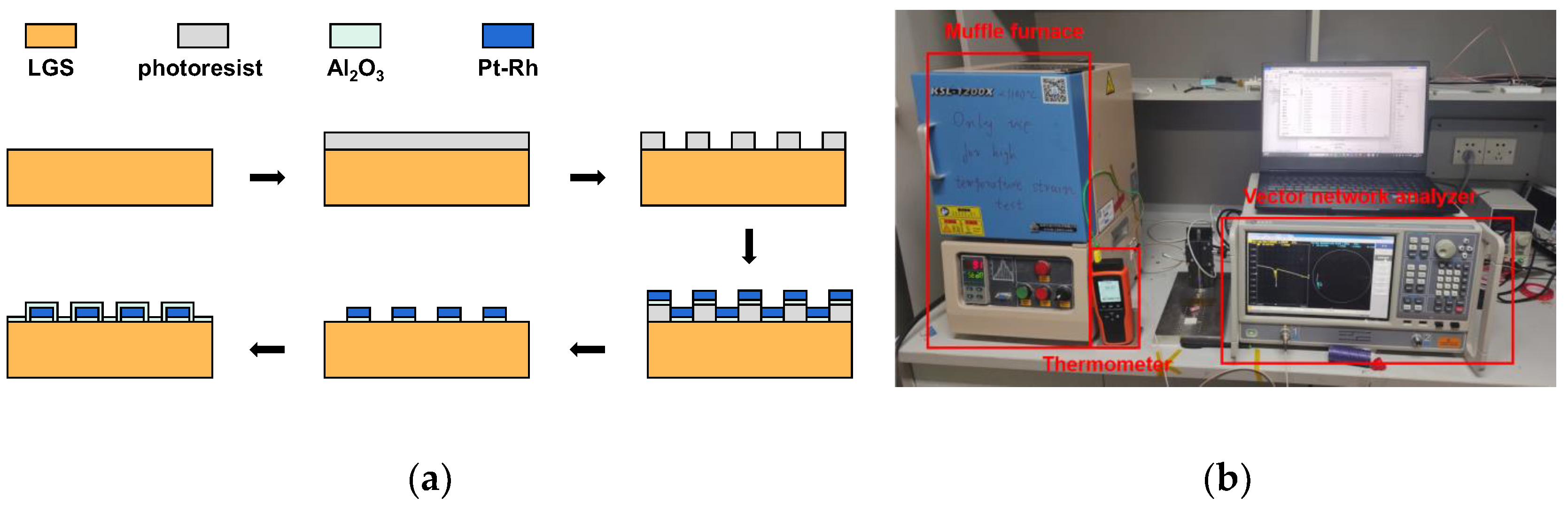
2.2. Fabrication and Temperature Measurement
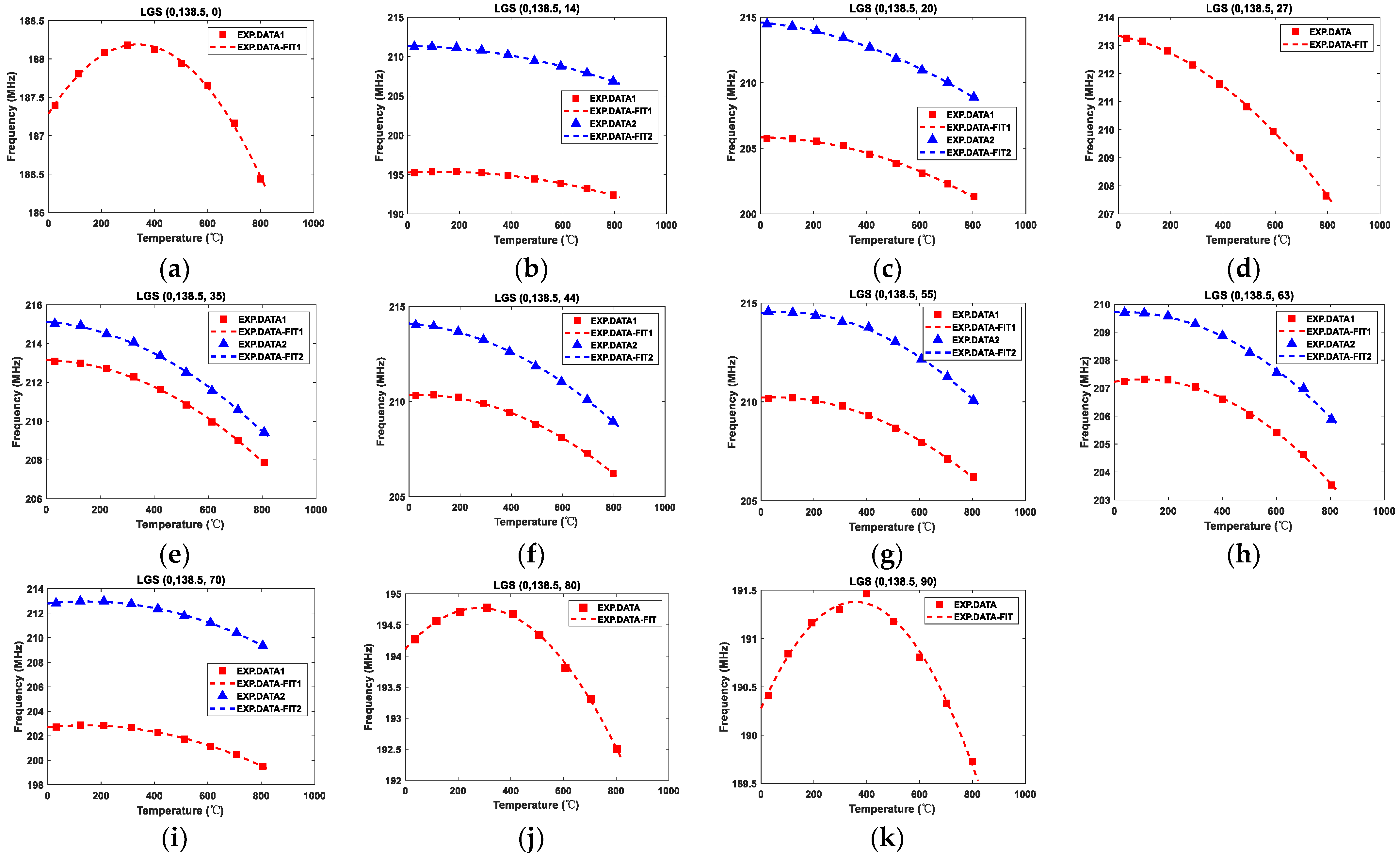
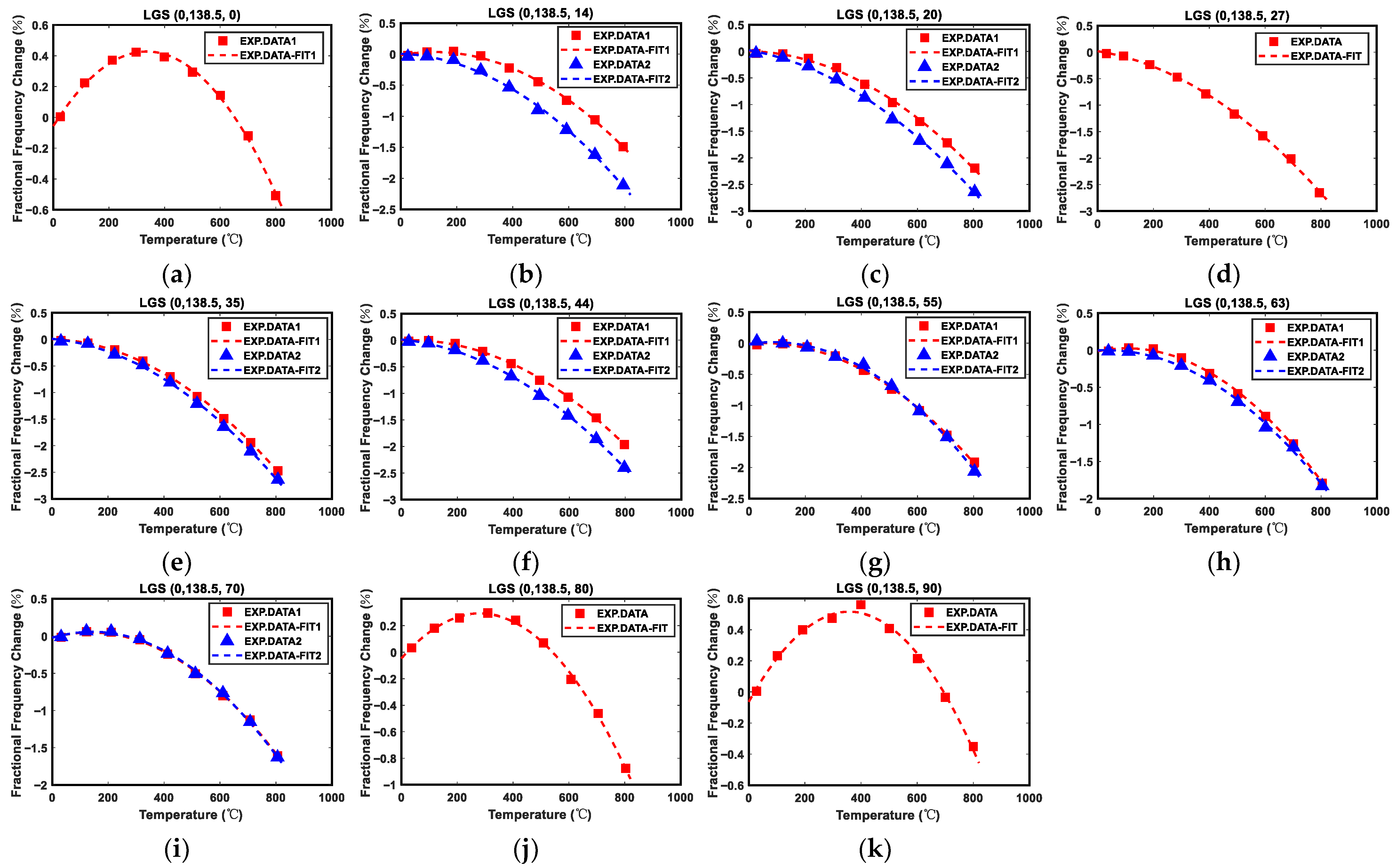
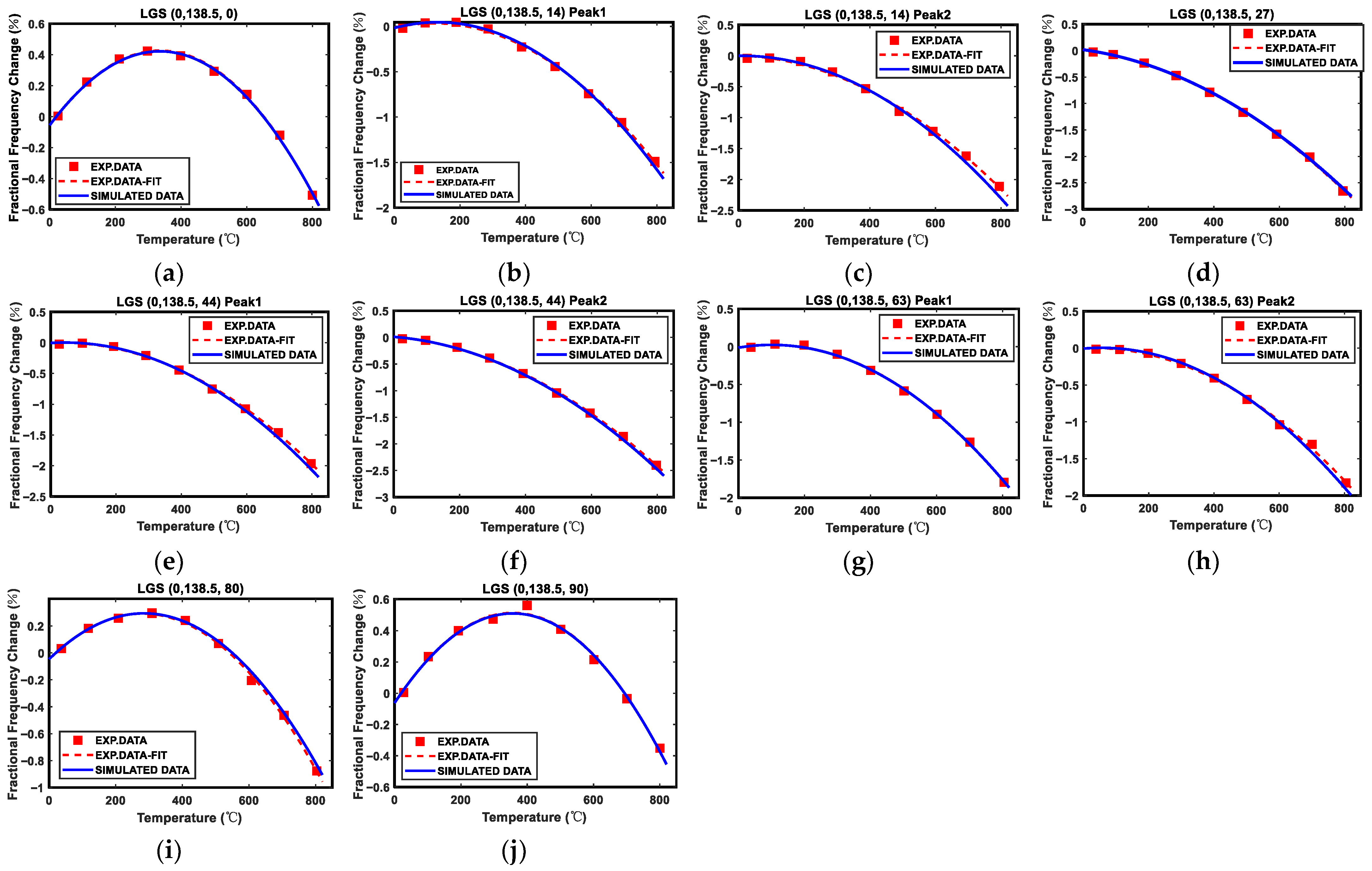
2.3. Data and Fitting Process
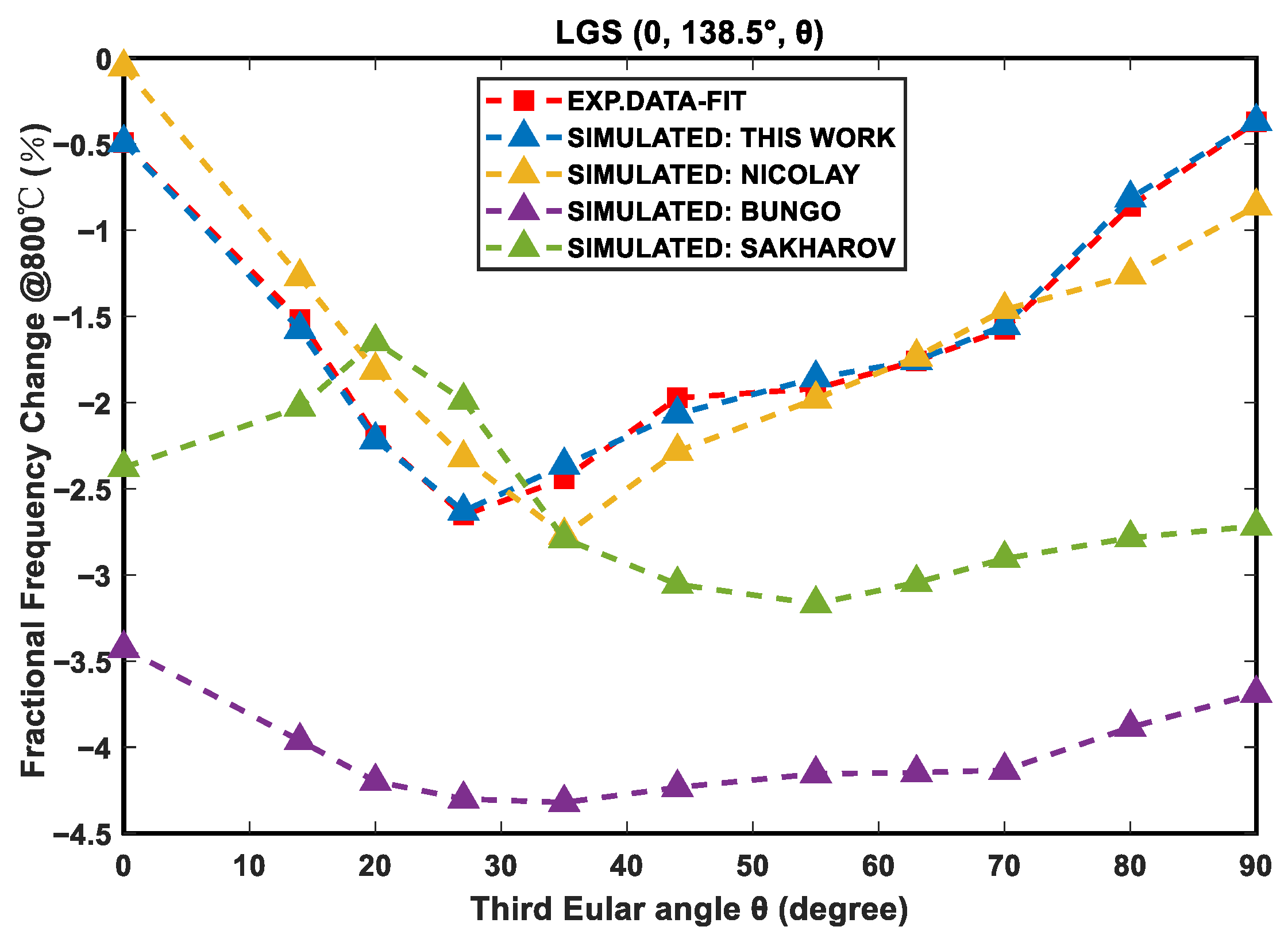
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Environetix Technology Corp. EVHT-100 Wireless Temperature Sensor System. 2013. Available online: https://inknowvation.com/sbir/awards/af-2013-strain-measurement-system-operation-extreme-environments (accessed on 10 December 2013).
- Zhou, X.; Tan, Q.; Liang, X.; Lin, B.; Guo, T.; Gan, Y. Novel Multilayer SAW Temperature Sensor for Ultra-High Temperature Environments. Micromachines 2021, 12, 643. [Google Scholar] [CrossRef] [PubMed]
- Bungo, A.; Jian, C.; Yamaguchi, K.; Sawada, Y.; Uda, S.; Pisarevsky, Y.P. Analysis of surface acoustic wave properties of the rotated Y-cut langasite substrate. Jpn. J. Appl. Phys. 1999, 38, 3239–3243. [Google Scholar] [CrossRef]
- Sakharov, S.; Senushencov, P.; Medvedev, A.; Pisarevsky, Y. New data on temperature stability and acoustical losses of langasite crystals. In Proceedings of the 1995 IEEE International Frequency Control Symposium (49th Annual Symposium), San Francisco, CA, USA, 31 May–2 June 1995; pp. 647–652. [Google Scholar] [CrossRef]
- Nakamura, N.; Sakamoto, M.; Ogi, H.; Hirao, M. Elastic constants of langasite and alpha quartz at high temperatures measured by antenna transmission acoustic resonance. Rev. Sci. Instrum. 2012, 83, 073901. [Google Scholar] [CrossRef] [PubMed]
- Nicolay, P.; Aubert, T. A Numerical Method to Derive Accurate Temperature Coefficients of Material Constants from High-Temperature SAW Measurements: Application to Langasite. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2013, 60, 2137–2141. [Google Scholar] [CrossRef] [PubMed]
- Malocha, D.C.; Da Cunha, M.P.; Adler, E.; Smythe, R.C.; Frederick, S.; Chou, M.; Helmbold, R.; Zhou, Y.S. Recent measurements of material constants versus temperature for langatate, langanite and langasite. In Proceedings of the Annual IEEE International Frequency Control Symposium, Kansas City, MO, USA, 9 June 2000; pp. 200–205. [Google Scholar]
- Bourquin, R.; Dulmet, B. Thermal sensitivity of elastic coefficients of langasite and langatate. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2009, 56, 2079–2085. [Google Scholar] [CrossRef] [PubMed]
- Bourquin, R.; Dulmet, B. New sets of data for the thermal sensitivity of elastic coefficients of langasite and langatate. In Proceedings of the 20th European Frequency and Time Forum, Braunschweig, Germany, 27–30 March 2006; pp. 26–32. [Google Scholar]
- Ji, X.; Han, T.; Shi, W.; Zhang, G. Investigation on SAW properties of LGS and optimal cuts for high-temperature applications. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2005, 52, 2075–2080. [Google Scholar] [CrossRef] [PubMed]



| Material Constants [6] @ 20 °C | First Order (ppm/°C) | Second Order (ppb/°C) | |
|---|---|---|---|
| (×1010 N/m2) | 18.89 | −83.5 | −38 |
| (×1010 N/m2) | 10.42 | −126.3 | −23 |
| (×1010 N/m2) | 10.15 | −89.9 | −78.4 |
| (×1010 N/m2) | 1.44 | −277.5 | 25.6 |
| (×1010 N/m2) | 26.83 | −107.3 | −24.2 |
| (×1010 N/m2) | 5.33 | −42.4 | −64.1 |
| −0.4371 | 617.8 | −356.9 | |
| 0.1039 | −866.3 | 1789.5 | |
| 19.05 | 134.5 | 118 | |
| 51.81 | −787 | 685.6 | |
| 5743 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mu, D.; Zhang, H.; Zhang, J.; Feng, Y.; Jin, H.; Dong, S. Extract Temperature Coefficients of LGS for High-Temperature Applications Based on the Finite Element Method. Eng. Proc. 2025, 110, 4. https://doi.org/10.3390/engproc2025110004
Mu D, Zhang H, Zhang J, Feng Y, Jin H, Dong S. Extract Temperature Coefficients of LGS for High-Temperature Applications Based on the Finite Element Method. Engineering Proceedings. 2025; 110(1):4. https://doi.org/10.3390/engproc2025110004
Chicago/Turabian StyleMu, Danyu, Hong Zhang, Jikai Zhang, Yan Feng, Hao Jin, and Shurong Dong. 2025. "Extract Temperature Coefficients of LGS for High-Temperature Applications Based on the Finite Element Method" Engineering Proceedings 110, no. 1: 4. https://doi.org/10.3390/engproc2025110004
APA StyleMu, D., Zhang, H., Zhang, J., Feng, Y., Jin, H., & Dong, S. (2025). Extract Temperature Coefficients of LGS for High-Temperature Applications Based on the Finite Element Method. Engineering Proceedings, 110(1), 4. https://doi.org/10.3390/engproc2025110004








