Abstract
The present work aims to predict the cyclic behavior and fatigue life of 316 FR stainless steel specimens at 650 °C. First, the samples were modeled using finite element analysis under different strain amplitudes, and the obtained numerical hysteresis loops were compared against experimental results available in the literature. Then, the fatigue life was estimated using different fatigue life prediction models, namely the Coffin–Manson model, Ostergren’s damage function, and Smith–Watson–Topper model, and was compared to the experimental fatigue life. The obtained results revealed that the numerical cyclic stress–strain data are in good agreement with those obtained experimentally. In addition, the predicted fatigue lives using the previously mentioned fatigue life models and based on the provided equation parameters are within a factor of 2.5 of the experimental results. Accordingly, it is suggested that they can be used to predict the fatigue life of 316 FR stainless steel.
1. Introduction
Advanced Gas-cooled Reactors (AGR) in the nuclear power plant industry are designed to operate at severe temperatures [1], resulting in thermal stresses occurring simultaneously with mechanical loads. Basically, the frequent start-up and shut-down procedures, as well as the change in power level owing to the daily energy consumption, are the main reason for these components experiencing combined mechanical and thermal cyclic loadings. The resulting repetitive loads cause microscopic damage to the material, which leads to fatigue crack initiation, propagation, and eventually, failure.
Over time, several fatigue life prediction approaches for the Low Cycle Fatigue (LCF) regime have been published in the literature; the most popular are the plastic strain-based approaches such as the Coffin–Manson model [2,3], strain energy-based criteria such the Smith–Watson–Topper (SWT) damage model [4], which can be used for both low- and high-cycle fatigue conditions, and Ostergren’s equation [5]. The two latest ones (i.e., SWT and Ostergren models) consider the effect of mean stress on fatigue life. Another well-known strain energy-based method worth mentioning is Golos and Ellyin’s total strain energy density approach [6] as it is valid for low and high cycle fatigue regimes, as well as for both Masing and non-Masing material response. Moreover, when using these equations, the accuracy of the stress–strain data is also important for estimating accurate low-cycle fatigue life. Finite Element Analysis (FEA) is one of the most effective tools to use, since it has been shown to be precise and accurate [7,8].
Materials with good cyclic characteristics are generally required for use in AGRs to withstand severe low cycle fatigue loadings. 316FR Stainless Steel (SS) is identical to 316LN SS [7,8], a low-carbon increased nitrogen grade of austenitic stainless steel that is typically selected for this sort of application due to its extending mechanical, low-cycle fatigue and creep properties at higher temperatures [1].
Many research investigations have been undertaken in the last few years to examine the durability of 316 SS under low-cycle fatigue at room temperature, in particular [7,8,9], but few studies have been dedicated to low-cycle fatigue at higher temperatures. Hormozi [1], for example, performed thorough experimental and numerical investigations of isothermal and in-phase thermomechanical low cycle fatigue of 316 FR SS with and without hold time. As a result, he developed a substantial number of findings related to the analysis of stress–strain data, cyclic plasticity behavior, and creep-fatigue damage evolution for low-cycle fatigue and thermomechanical fatigue conditions.
Recently, a vast majority of investigations have been conducted to study the accuracy of the widely used low-cycle fatigue life equations, namely the Coffin–Manson [2,3], Smith–Watson–Topper [4], and Ostergren models [5] at room temperature, in particular [10,11]. However, only a few studies have focused on determining the parameters and evaluating the accuracy of these LCF models, for 316 stainless steel, at higher temperatures. In the present paper, the cyclic stress–strain curves have been generated based on finite element analysis and have been compared with the experimental ones found by Hormozi [1]. Then, an examination of the aforementioned low-cycle fatigue life prediction equations, i.e., the Coffin–Manson [2,3], Smith–Watson–Topper (SWT) [4], and Ostergren equations [5], has been made and the parameters of these equations have been proposed for dumbbell specimens made of 316 FR SS at 650 °C. The predicted fatigue lives have been compared with the test data provided by Hormozi [1], Hong et al. [12], and Tak et al. [13].
2. Experimental Conditions
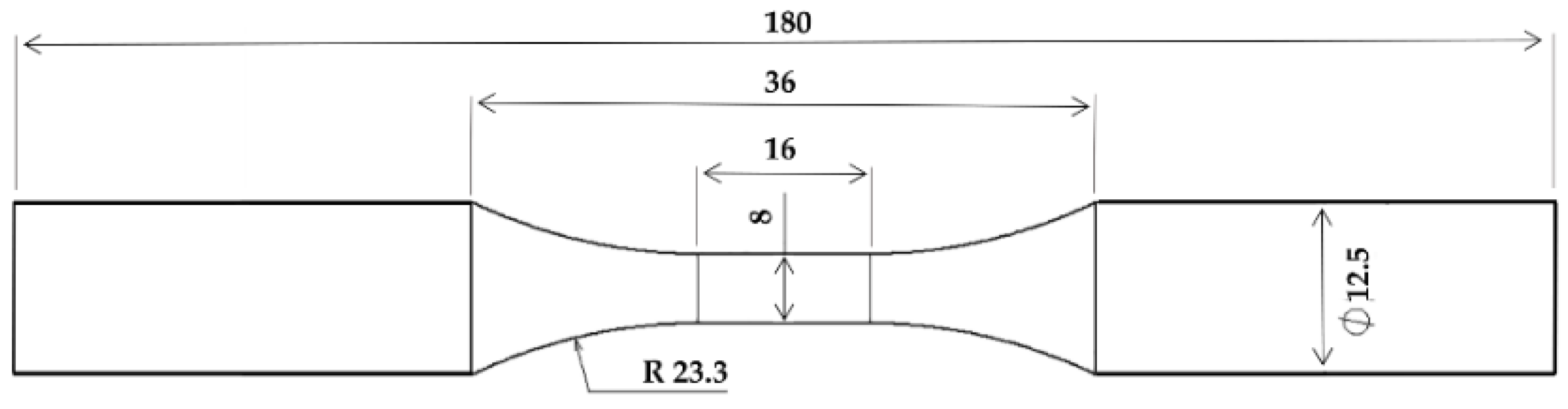
Hormozi [1] conducted a fully reversed uniaxial low-cycle fatigue experiment on four polished dumbbell specimens made of 316 FR SS, the chemical composition of which is indicated in Table 1 (in weight percent). The specimens have a gauge diameter and length of 8 and 16 mm, respectively, as shown in Figure 1. The LCF experiments were performed under different mechanical strain amplitude levels, namely ±0.4, ±0.8, ±1.0, and ±1.2%, and at a constant temperature of 650 °C. All the tests were undertaken in the air environment with a frequency of 0.01 Hz.

Table 1.
Chemical Composition of 316FR SS in weight (%) [1].
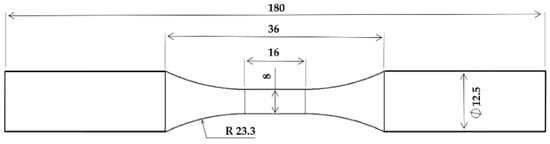
Figure 1.
Specimens shape and dimensions (in mm).
3. Finite Element Analysis
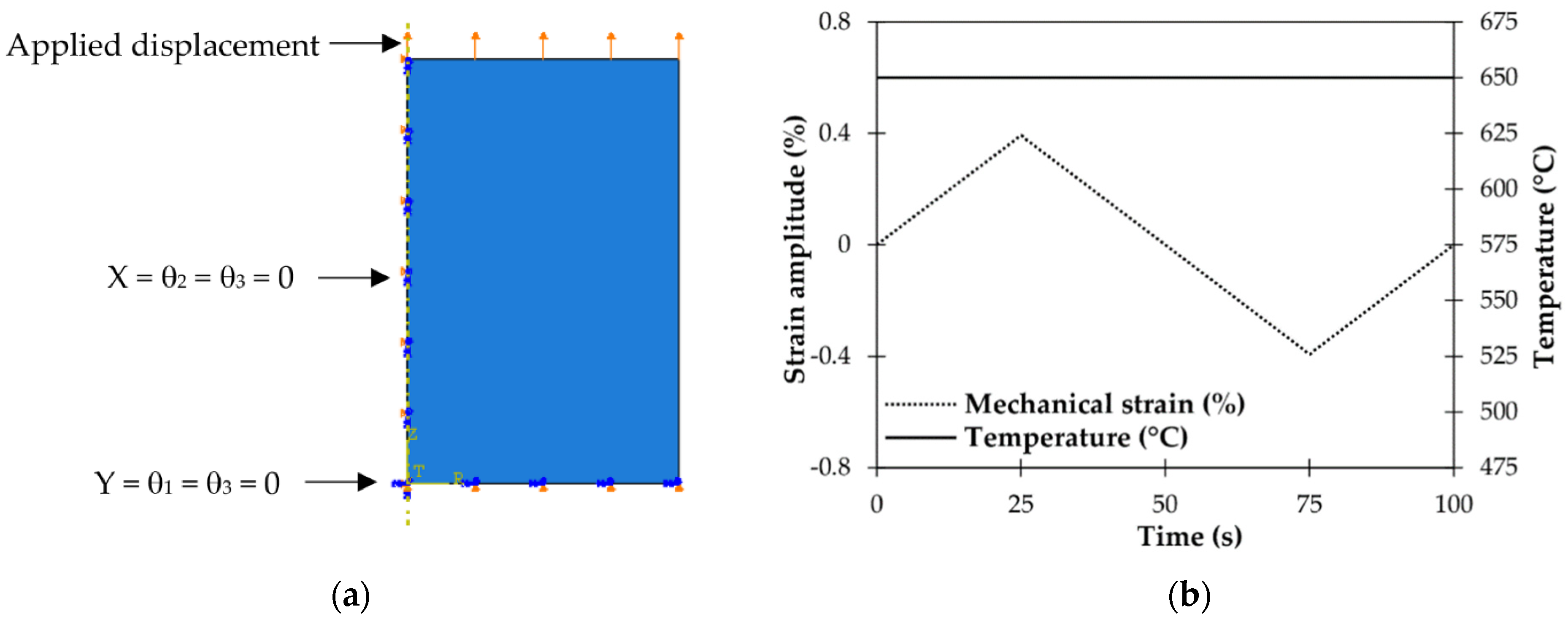
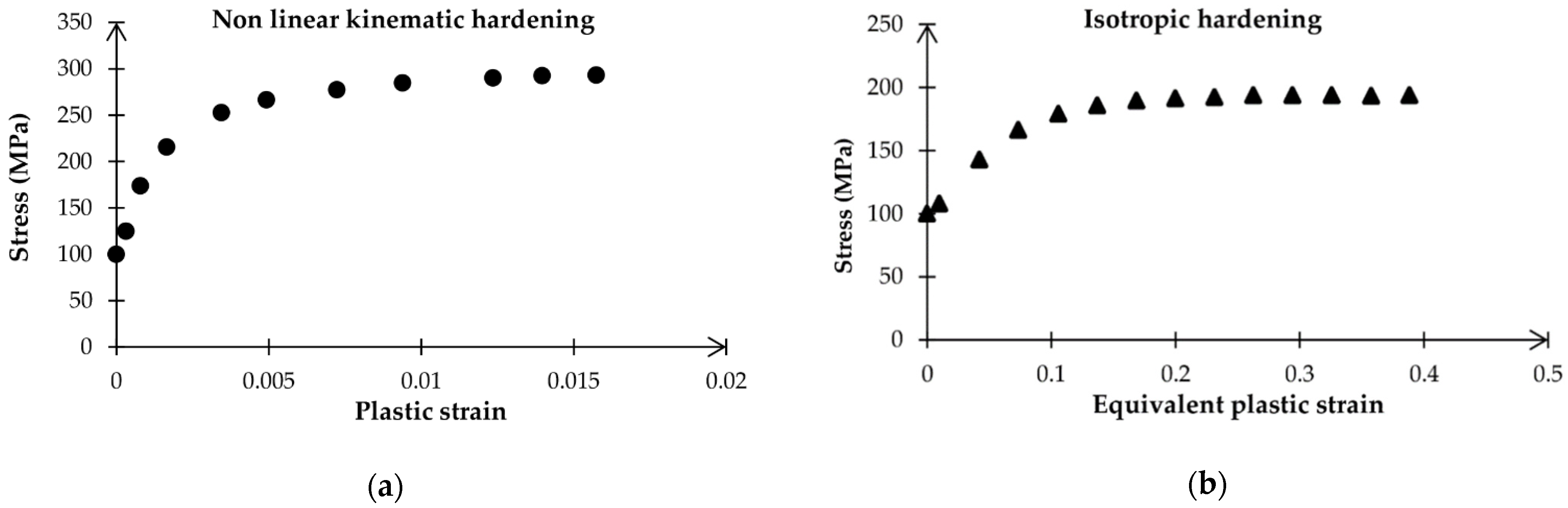
Finite element analysis has been conducted on four cylindrical specimens using ABAQUS software [14]. The 2D-axisymmetric model, with a radius of 4 mm and a height of 6.25 mm, has been created to illustrate the gauge section of the samples under study. As shown in Figure 2a, symmetry boundary conditions have been generated along the gauge length and gauge diameter, and prescribed cyclic displacement has been applied to the higher extremity of the 2D model in a symmetrical triangular waveform as illustrated in Figure 2b. Moreover, the temperature was fixed and set to 650 °C. The CAX4R elements have been considered in the mesh section. The kinematic and isotropic plasticity data from [1], as well as other material properties, represented in Figure 3 and Table 2, respectively, have been implemented in the FEA software’s property section.
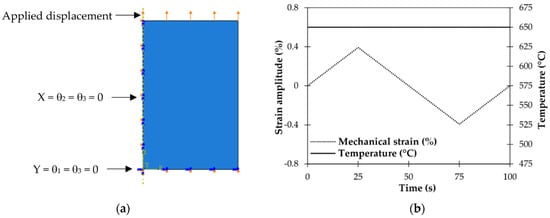
Figure 2.
Representation of the finite element model on Abaqus; (a) boundary conditions, and (b) applied loads waveform.
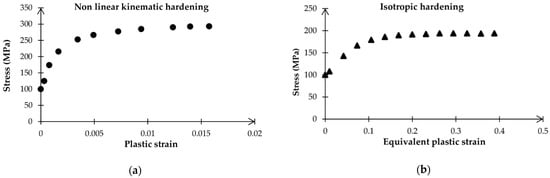
Figure 3.
Plasticity data of (a) non-linear kinematic hardening, and (b) isotropic hardening of 316 FR SS, at 650 °C, for a strain amplitude of ±1.0% [1].

Table 2.
Material properties of 316 FR SS at 650 °C [1].
4. Results & Discussion
4.1. Cyclic Stress–Strain Response
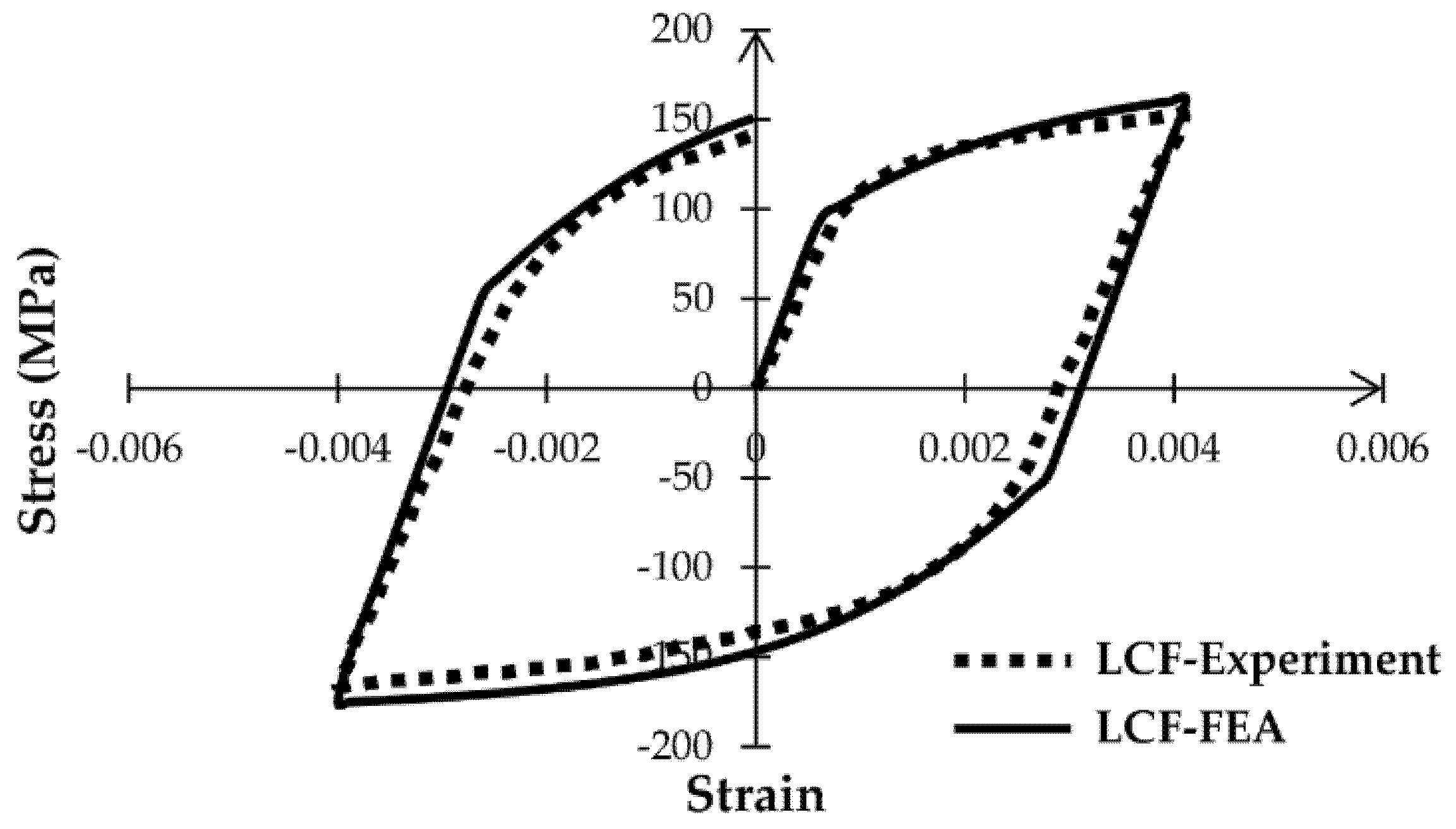
The estimated cyclic stress–strain data at ±0.4% have been compared to Hormozi’s experimental results [1]. As shown in Figure 4, the numerically estimated hysteresis loops are in good agreement with those found experimentally. As a result, the FE data are accurate and can be used to predict the low-cycle fatigue life of 316 FR SS.
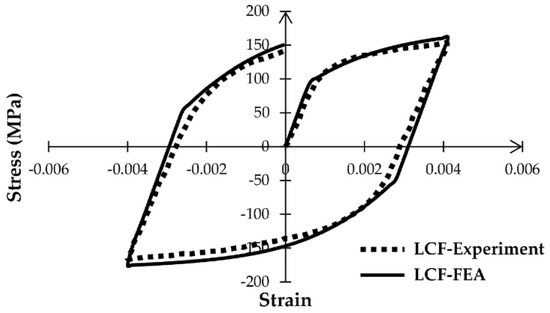
Figure 4.
Comparison between the numerical hysteresis loop and the experimental one provided by Hormozi [1] under ±0.4% strain amplitude.
4.2. Fatigue Life Prediction
This section covers the evaluation of the well-known fatigue life equations for estimating the low-cycle fatigue life for dumbbell specimens made of 316 FR SS at 650 °C. These include the Coffin–Manson, Ostergren, and Smith–Watson–Topper models [2,3,4,5]. The predicted fatigue lives found from the present study will be compared with the test results reported in [1,12,13].
4.2.1. Coffin–Manson Model
In the low-cycle regime, Coffin and Manson [2,3] independently established a log–log linear equation to consider the effect of plastic strain range ∆εp on the low-cycle fatigue life Nf. The well-known Coffin–Manson equation is given as follows:
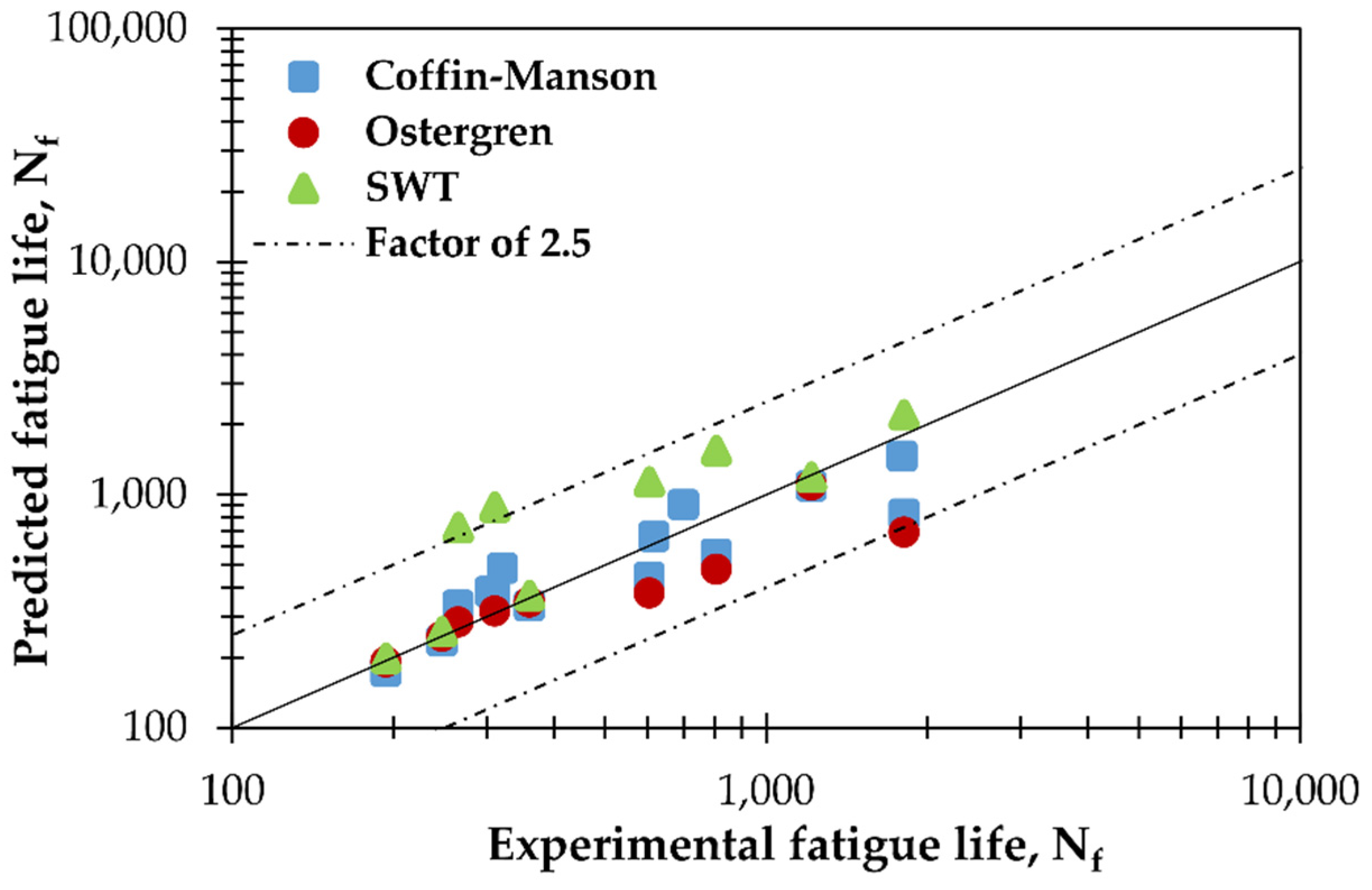
where , and are the fatigue ductility coefficient and fatigue ductility exponent, respectively. The values of these two material parameters at 650 °C, obtained by the least square regression technique with a coefficient of determination R2 of 0.998, are listed in Table 3. The numerically and experimentally obtained plastic strain amplitudes at the saturation stage, for each applied mechanical strain amplitude, are provided in Table 4. In this table (i.e., Table 4), the Relative Error (RE) between the experimental and numerical plastic strain amplitude values, for all applied strain amplitudes, shows that the finite element model accurately predicts the plastic strains under LCF conditions. The estimated fatigue lives obtained using Equation (1) were compared to those provided by Hormozi [1] and are found to be conservative with an average relative error of −7.87% and lie very close to a factor of 1, as illustrated in Figure 5. For further validation, the obtained predicted fatigue lives from the Coffin–Manson model were also compared to 10 test data points provided by Hong et al. [12], and Tak et al. [13] for a mechanical strain amplitude between ±0.4 and ±0.8% and found to fall within a factor of 2.5 of the test results, as shown in Figure 5. Hence, the suggested parameters in Table 3 are valid and can be used to predict the fatigue life of the present study’s used material when the temperature is 650 °C.

Table 3.
Coffin–Manson, Ostergren and SWT equations parameters for 316 FR SS at 650 °C.

Table 4.
Relative error between the predicted and experimental [1] maximum stress and plastic strain amplitude.
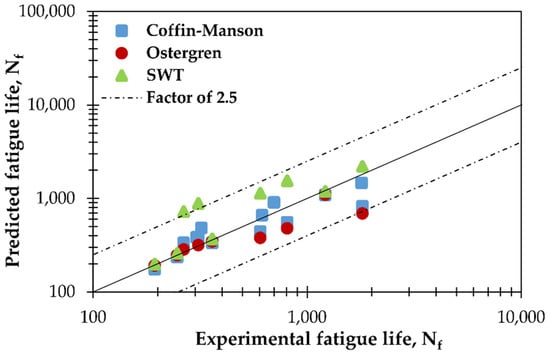
Figure 5.
Comparison of the predicted fatigue life with the experimental results in [1,12,13].
4.2.2. Ostergren Damage Model
Ostergren [5] proposed a damage function that relates the plastic strain range ∆εp and the maximum stress σmax to the fatigue life Nf as follows:
where L and n are material parameters. The obtained values for each by the least square regression technique with an R2 of 0.997 are represented in Table 3.
The FE obtained maximum stress for each applied strain amplitude is listed in Table 4. The percentage relative error between the FE predicted peak stress and the experimental one further indicates that the FE results are in good agreement with those found experimentally. Moreover, the calculated fatigue life using Equation (2) are plotted against the experimental data in Figure 5. As can be seen, the estimated low cycle fatigue life using the Ostergren damage function [4] lies extremely close to the factor of 1, and the maximum relative error is only −9.41% at 0.4% strain amplitude. The comparison between the predicted fatigue lives using the Ostergren model and the experimental data of Hong et al. [12] shows that the fatigue life is conservative at 0.4, 0.5, and 0.6% strain amplitudes and with a more significant relative error than at 0.7 and 0.8% strain amplitude. By way of example, the relative error is −37.36 and 2.5% for strain amplitudes of 0.6 and 0.7%, respectively. Accordingly, the overall predicted results are within a factor of 2.5 of the test data. Thus, one can conclude that the Ostergren model along with the proposed parameters in Table 3 can well predict the low cycle fatigue life of 316 FR SS, at 650 °C.
4.2.3. Smith–Watson–Topper Damage Model
Smith et al. [4] presented the SWT parameter (i.e., σmax Δε) as a damage parameter that is related to cycle life in the following [15]:
where Δε is the mechanical strain range, and β and C are material constants.
The fatigue lives calculated using Equation (3) with the parameters listed in Table 3 (R2 of 1), under different strain amplitudes, have been compared with those obtained experimentally [1]. As observed from Figure 5, the predicted LCF life by means of Equation (3) along with the SWT material parameters represented in Table 3, are in good agreement with the experimental ones (factor of 1), and the maximum relative error is only 4.71% at the strain amplitude of 1%. Further validation with test data from reference [12] was made, and the predicted fatigue lives are found to have a factor of 2.5 as shown in Figure 5. Therefore, it may be concluded that the Smith–Watson–Topper equation along with the present study’s supplied parameters can correctly estimate the fatigue life for 316 FR SS at 650 °C.
5. Conclusions
In this work, the cyclic stress–strain response of 316 FR SS at 650 °C has been numerically obtained using FEA and compared to the experimental results in order to examine the accuracy of the finite element model. The fatigue life has been estimated for various applied strains at the same mentioned temperature and compared to the experimental data provided in the literature [1,12,13] to assess the accuracy of the commonly used fatigue life equations, namely the Coffin–Manson, Ostergren, and Smith–Watson–Topper models [2,3,4,5]. The following conclusions have been made; (1): the cyclic stress–strain data were found to be in good agreement with the experimental results. (2): The fatigue life equations parameters that were found using least square regression analysis have been supplied. (3): The fatigue life prediction models with the given parameters yielded results that were close to the experimental findings by a factor of 2.5. Hence, it is suggested that these fatigue life equations can be used to accurately estimate the fatigue life of 316 FR SS at 650 °C.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/ASEC2021-11116/s1.
Author Contributions
Conceptualization, methodology, formal analysis, investigation, writing—original draft preparation, I.A.; validation, writing—review and editing, A.K. and R.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data can be made available on demand.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hormozi, R. Experimental and Numerical Simulations of Type 316 Stainless Steel Failure under LCF/TMF Loading Conditions. Ph.D. Thesis, Imperial College, London, UK, 2014. [Google Scholar]
- Coffin, L.F., Jr. A Study of the Effects of Cyclic Thermal Stresses on a Ductile Metal; Knolls Atomic Power Laboratory: Schenectady, NY, USA, 1953.
- Manson, S.S. Behavior of Materials under Conditions of Thermal Stress; National Advisory Committee for Aeronautics: Washington, DC, USA, 1954. [Google Scholar]
- Smith, K.N.; Watson, P.; Topper, T.H. A stress-strain function for the fatigue of metals. J. Mater. 1970, 5, 767–778. [Google Scholar]
- Meltzer, R.; Fiorini, Y.; Horstman, R.; Moore, I.; Batik, A.; Ostergren, W. A Damage Function and Associated Failure Equations for Predicting Hold Time and Frequency Effects in Elevated Temperature, Low Cycle Fatigue. J. Test. Eval. 1976, 4, 327. [Google Scholar] [CrossRef]
- Golos, K.; Ellyin, F. Total strain energy density as a fatigue damage parameter. In Advances in Fatigue Science and Technology; Springer: Dordrecht, The Netherlands, 1989; Volume 159, pp. 849–858. [Google Scholar] [CrossRef]
- Abarkan, I.; Shamass, R.; Achegaf, Z.; Khamlichi, A. Numerical and analytical studies of low cycle fatigue behavior of 316 LN austenitic stainless steel. J. Press. Vessel Technol. 2020. [Google Scholar] [CrossRef]
- Abarkan, I.; Khamlichi, A.; Shamass, R. A Study on low cycle fatigue life assessment of notched specimens made of 316 LN austenitic stainless steel. J. Press. Vessel. Technol. 2022, 144, 021503. [Google Scholar] [CrossRef]
- Roy, S.C.; Goyal, S.; Sandhya, R.; Ray, S. Low cycle fatigue life prediction of 316 L(N) stainless steel based on cyclic elasto-plastic response. Nucl. Eng. Des. 2012, 253, 219–225. [Google Scholar] [CrossRef]
- Dutta, A.; Dhar, S.; Acharyya, S.K. Material characterization of SS 316 in low-cycle fatigue loading. J. Mater. Sci. 2010, 45, 1782–1789. [Google Scholar] [CrossRef]
- Yuan, X.; Yu, W.; Fu, S.; Yu, D.; Chen, X. Effect of mean stress and ratcheting strain on the low cycle fatigue behavior of a wrought 316LN stainless steel. Mater. Sci. Eng. A 2016, 677, 193–202. [Google Scholar] [CrossRef]
- Hong, S.G.; Yoon, S.; Lee, S.B. The effect of temperature on low-cycle fatigue behavior of prior cold worked 316L stainless steel. J. Fatigue 2003, 25, 1293–1300. [Google Scholar] [CrossRef]
- Tak, N.H.; Kim, J.S.; Lim, J.Y. An Energy-Based Unified Approach to Predict the Low-Cycle Fatigue Life of Type 316L Stainless Steel under Various Temperatures and Strain-Rates. Materials 2019, 12, 1090. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- ABAQUS/Standard, version 6.14; Dassault Systèmes Simulia Corp.: Providence, RI, USA, 2014.
- Bartošák, M. Phenomenological Models for Lifetime Prediction under Low-Cycle Fatigue and Thermo-Mechanical Fatigue Loading Conditions. Ph.D. Thesis, Czech Technical University, Prague, Czech Republic, 2019. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).