Abstract
This paper presents the mathematical modeling of the thermal state of a 1000 W wind turbine generator (WTG) integrated into a vertical-axis wind turbine (VAWT) system, taking into account external environmental factors, mechanical losses, and the operation of the cooling system. The developed model considers the influence of ambient temperature, wind speed, air humidity, ventilation openings, radiator cooling, and mechanical losses. An analysis was conducted over a range of operating conditions from −20 °C to 50 °C, with wind speeds from 0.5 m/s to 15 m/s and air humidity from 10% to 90%. The nonlinear dependence of the winding temperature on these factors was investigated, and critical operating conditions leading to potential overheating were identified. It was found that high humidity (>70%) increases the winding temperature by 5–10% compared to low humidity (<30%). The developed model can be used to optimize cooling systems and improve the reliability of wind turbines in various climatic conditions. In addition, the proposed model is intended to be integrated into fault detection and diagnosis systems for wind turbines, enabling the identification of potential faults related to thermal overload.
1. Introduction
Currently, renewable energy sources play a key role in the development of the energy sector by providing a sustainable power supply and reducing negative environmental impacts. Vertical-axis wind turbines (VAWTs) are gaining increased attention due to their compact design, independence from wind direction, and high operational reliability [1]. Among the various challenges associated with wind power systems, thermal management of the generator remains a critical issue, especially under varying external environmental conditions. Overheating of generator windings can lead to reduced operational efficiency, accelerated degradation of insulation materials, and potential equipment failures [2]. Therefore, the development of a mathematical model capable of predicting the thermal behavior of wind turbine generator windings under diverse operating conditions is of great practical importance. Such conditions include ambient temperature, wind speed, air humidity, mechanical losses, and the performance of cooling systems.
This paper focuses on the mathematical modeling of the thermal state of a 1000 W vertical-axis wind turbine. The proposed model takes into account external environmental factors, internal mechanical losses, and the efficiency of cooling mechanisms. The study aims to identify the generator’s critical operating thresholds and offer insights for optimizing the cooling system in order to enhance the reliability and longevity of wind turbine generators operating in different climatic conditions.
2. Materials and Methods
This study investigates the thermal state of a 1000 W vertical-axis wind turbine. The wind turbine generator is equipped with three DHT11 temperature and humidity sensors mounted on its windings (Figure 1). The main objective of the research is to develop a mathematical model for a diagnostic system that accounts for the influence of varying external conditions—such as ambient temperature, wind speed, and air humidity—as well as mechanical losses and different cooling methods, including ventilation, heat sinks, and convection.

Figure 1.
Installation of temperature sensors on generator windings.
Main parameters of the wind turbine generator [3]:
- -
- Power output: 1000 W;
- -
- Generator type: Three-phase with synchronous windings;
- -
- Winding material: Copper;
- -
- Rotor diameter: 1.2 m;
- -
- Blade height: 1.8 m;
- -
- Rotational speed at rated power: 250–300 RPM;
- -
- Generator power factor: 0.38.
To model the thermal state of the wind turbine generator, differential equations of heat transfer, rotor aerodynamic characteristics, and mechanical loss modeling were employed. The analysis was carried out over an extended range of operating conditions, with ambient temperatures ranging from −20 °C to +50 °C and wind speeds from 0.5 m/s to 15 m/s.
As part of the thermal model development, the aerodynamic power transferred to the rotor was determined. The wind energy captured by the wind turbine is calculated using the following formula [4]:
where Pw—wind power available for conversion (W); ρ—air density (kg/m3); A—rotor swept area (m2); C—power coefficient of the wind generator; and V—wind speed (m/s).
Air density ρ is a critical parameter in the thermal state calculations of a wind turbine, as it directly affects the amount of energy transferred from the wind to the rotor. It varies depending on the ambient temperature, as well as atmospheric pressure and air humidity. In this model, air density is calculated using the ideal gas law, enabling the consideration of varying thermal conditions during wind turbine operation [5]:
where p—atmospheric pressure; R—specific gas constant for air (J/(kg·K)); and Ts—ambient temperature (°C).
The rotational dynamics of the rotor are described by the law of conservation of angular momentum [4,5], which takes into account the various torques acting on the system:
where J is the moment of inertia of the rotor (kg·m2), representing the resistance of the rotor to changes in rotational speed; Twind is the torque produced by the wind acting on the rotor (N·m), which serves as the driving force in the system; μ is the viscous friction coefficient (N·m·s), accounting for internal mechanical damping in the system; ω is the angular velocity of the rotor (rad/s); Text is the external braking torque (N·m), which may be applied for control or safety purposes; Tfriction is the torque due to mechanical friction in bearings and other rotating components (N·m); and Taero is the aerodynamic drag torque acting against the motion of the blades (N·m).
This equation forms the basis for analyzing the dynamic response of the wind turbine and is crucial for predicting performance, optimizing control strategies, and integrating thermal and mechanical models.
The following system of equations describes the electrical and thermal behavior of a wind turbine generator [6]. Each expression reflects key physical processes involved in the operation of electromagnetic machines under varying environmental influences such as temperature, wind speed, and ventilation efficiency. Generator Output Voltage—Faraday’s Law of Electromagnetic Induction:
This equation represents the core principle of electromagnetic induction, where the induced electromotive force (EMF) in a coil is proportional to the rate of change of magnetic flux density dB/dt and the number of coil turns N. In the context of a wind turbine, the rotor motion causes a variation in magnetic flux through the stator windings, thus generating voltage. This equation forms the basis for simulating voltage generation under dynamic wind conditions.
Temperature Dependence of Coil Resistance [7]:
where R(T) is the resistance at temperature T (°C), Rn is the reference resistance at 20 °C, α is the temperature coefficient of resistivity for copper (typically ≈ 0.00393 °C−1), and T is the operating temperature in degrees Celsius.
An accurate estimation of winding resistance is essential for calculating power losses due to Joule heating and for evaluating the system’s thermal response over time. Thermal balance of generator windings [8]:
where m is the mass of the windings (kg), c is the specific heat capacity of the winding material (J/kg·°C), is the power loss due to electrical resistance (Joule heating), is the power loss due to mechanical effects (e.g., friction), and is the total heat loss through the generator housing and cooling system (W).
This equation is crucial for evaluating how quickly the generator heats up under load and how well the system can maintain thermal stability over time.
Heat loss through ventilation and housing [9,10]:
where T is the winding temperature (°C), is the ambient temperature (°C), and is the equivalent thermal resistance (°C/W), which accounts for insulation, the generator casing, radiators, and ventilation effectiveness.
The lower the thermal resistance, the more efficiently the system can dissipate heat. This equation helps identify thermal bottlenecks and optimize the cooling design.
The system of coupled differential equations (Equations (5)–(7)) is numerically solved using the classical fourth-order Runge–Kutta method implemented in Python, offering an effective compromise between computational efficiency and numerical accuracy. This approach enables detailed simulation of both transient and steady-state behavior of the generator under varying environmental conditions. The analysis considers a broad range of ambient temperatures (from −20 °C to +50 °C), wind speeds (from 0.5 m/s to 15 m/s), and ventilation surface areas (from 0.02 m2 to 0.15 m2). By systematically varying these parameters, the model provides insight into how external conditions affect the generator’s output voltage, internal thermal response, and overall performance. The simulation results support the optimization of system design, including improvements to passive and active cooling strategies, material selection, and load management techniques.
3. Results and Discussion
This section presents the results of numerical simulations conducted to evaluate the thermal behavior of a 1000 W wind turbine generator, based on the previously developed mathematical model. The analysis focuses on the influence of ambient temperature, wind speed, mechanical losses, and various cooling methods on the temperature profile of the generator windings. Different operational scenarios were simulated, and critical conditions were identified under which thermal overload and overheating of the system may occur. To carry out the simulations, a custom Python-based computational tool was developed. This tool integrates sensor data (as shown in Figure 1) along with environmental parameters relevant to real-world operation. Climatic data were obtained from the meteorological database of gismeteo.kz, reflecting typical conditions in the city of Almaty. These inputs provided a realistic basis for evaluating the generator’s thermal performance under various weather scenarios and operational loads.
The obtained results allow for a comparative assessment of system behavior under different cooling strategies, helping to determine the effectiveness of passive and forced ventilation, as well as to define thermal safety margins for the generator in harsh climatic environments.
Figure 2 illustrates the simulated temperature behavior of the generator windings under varying environmental conditions. The left part of the figure shows the dependence of winding temperature on ambient temperature for several wind speeds: approximately 2.6 m/s (yellow), 5.7 m/s (orange), 8.9 m/s (red), and 12.0 m/s (violet). As the ambient temperature increases, the winding temperature also rises; however, higher wind speeds enhance cooling efficiency, resulting in significantly lower winding temperatures under identical conditions. The right part of the figure presents the dependence of winding temperature on wind speed at different fixed ambient temperatures: approximately 0 °C (red), 20 °C (orange), and 40 °C (yellow). It is clearly seen that increasing the wind speed leads to a rapid drop in winding temperature, especially at higher ambient temperatures. These results demonstrate the combined influence of thermal and airflow factors on the generator’s thermal behavior and emphasize the importance of adequate ventilation for preventing overheating under varying climatic conditions.
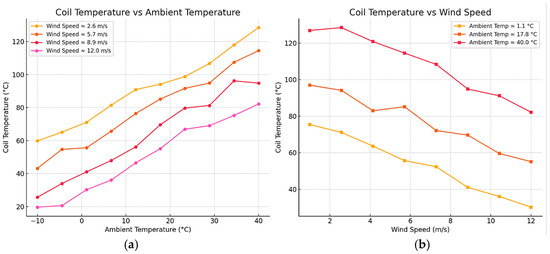
Figure 2.
Temperature behavior of the generator windings under different environmental conditions: (a) Dependence of coil temperature on ambient temperature for various wind speeds; (b) dependence of coil temperature on wind speed for different ambient temperatures.
One of the key factors influencing the thermal condition of the generator is the ambient air temperature. Simulation results have shown that as the ambient temperature rises above 30 °C, the temperature of the windings also increases significantly. This is primarily due to the reduced effectiveness of natural convection and radiative heat dissipation at higher environmental temperatures. Under extreme conditions, particularly when the ambient temperature reaches 40–50 °C, the absence of additional cooling mechanisms can lead to critical overheating. In such cases, the winding temperature may exceed 140–160 °C, which is above the maximum allowable operating range for most standard insulation materials. This can result in accelerated material degradation, reduced equipment lifespan, or even thermal failure.
To further explore the factors affecting the thermal behavior of the generator, mathematical modeling was extended to include the impact of air humidity on heat transfer efficiency. For this purpose, a new database was created, incorporating a range of humidity parameters. This allows for a more comprehensive analysis of winding temperature behavior under combined thermal and atmospheric conditions, including scenarios relevant to humid climates and tropical environments.
Based on the simulation results, the outcomes are presented in Figure 3.
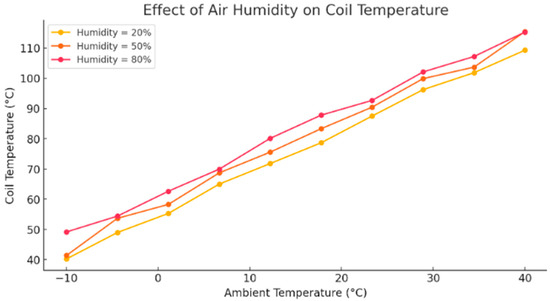
Figure 3.
Effect of air humidity on coil temperature.
The results of the study demonstrate that air humidity has a significant impact on the thermal behavior of wind turbine generator windings. Under high humidity conditions (greater than 70%), the temperature of the windings increases by approximately 5–10% compared to scenarios with low humidity levels (below 30%). This temperature rise is primarily attributed to changes in the thermophysical properties of air, particularly its heat capacity and reduced effectiveness in transferring heat away from the generator surfaces. High humidity decreases the air’s ability to absorb and carry away thermal energy, which in turn limits the efficiency of natural convective cooling. As a result, heat accumulates in the system more rapidly, leading to elevated winding temperatures and potentially accelerating insulation aging or degradation. These findings highlight the need to consider humidity as a critical environmental factor when assessing thermal loads and designing cooling strategies for wind energy systems operating in humid climates.
4. Conclusions
The developed mathematical model of the thermal state of a wind turbine generator has made it possible to identify the key factors influencing the temperature of the generator windings. These include ambient temperature, wind speed, air humidity, mechanical losses, and the effectiveness of cooling systems. The simulation-based analysis revealed that under conditions of high ambient temperatures (above 40 °C) combined with low wind speeds (below 3 m/s), the winding temperature can rise to 150 °C or higher. Such thermal levels exceed safe operating limits for standard insulation materials and therefore necessitate the implementation of active cooling measures.
The introduction of additional ventilation openings (greater than 0.1 m2) and heat sinks has proven effective, reducing winding temperatures by approximately 30–50% under critical conditions. Air humidity also plays a substantial role: at high humidity levels (above 70%), the temperature of the windings increases by 5–10%, which is attributed to the reduced efficiency of heat dissipation due to changes in the air’s thermophysical properties.
Mechanical losses—such as friction and aerodynamic drag—further contribute to internal heating, potentially raising the winding temperature by an additional 5–10%. These findings emphasize the importance of a comprehensive approach to thermal management, particularly in harsh or variable climate zones.
For the reliable long-term operation of wind turbine generators, it is recommended to regularly monitor bearing wear, maintain the cleanliness of the ventilation channels, and account for the minimum operational wind speed in system design and control. Future developments of the model may incorporate variable electrical loading, air pollution effects (e.g., dust accumulation), and extreme climate scenarios to further enhance prediction accuracy and system resilience.
Author Contributions
Conceptualization, A.F., Y.N. and B.T.; methodology, A.F., Y.N., G.V.R., B.T., T.I. and I.S.; software, A.F., Y.N., G.V.R. and B.T.; validation, A.F., Y.N. and T.I.; formal analysis, I.S.; investigation, A.F. and Y.N.; resources, G.V.R., B.T. and T.I.; data curation, B.T. and I.S.; writing—original draft preparation, A.F. and Y.N.; writing—review and editing, A.F., B.T. and T.I.; visualization, T.I. and I.S.; supervision, A.F.; project administration, B.T.; funding acquisition, A.F. and B.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Committee of Science of the Ministry of Science and Higher Education of the Republic of Kazakhstan, Grant No: AP19679162. This article is based on research conducted within the framework of the project “Development of a control and monitoring system for a multi-blade vertical-axis wind generator”.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The dataset is available from the authors upon request.
Acknowledgments
This article is based on research conducted within the framework of the project “Development of a control and monitoring system for a multi-blade vertical-axis wind generator” of the Committee of Science of the Ministry of Science and Higher Education of the Republic of Kazakhstan (Grant No: AP19679162).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Al-Rawajfeh, M.A.; Gomaa, M.R. Comparison between horizontal and vertical axis wind turbine. Int. J. Appl. Power Eng. IJAPE 2023, 12, 13–23. [Google Scholar] [CrossRef]
- Liu, H.; Wang, Y.; Zeng, T.; Wang, H.; Chan, S.-C.; Ran, L. Wind turbine generator failure analysis and fault diagnosis: A review. IET Renew. Power Gener. 2024, 18, 3127–3148. [Google Scholar] [CrossRef]
- Omer, D.; Ahmed, K.; Fawaz, D.; Abdullah, S.; Ali, D.; Hamoodi, N. Modeling and analysis of 1kW Wind Turbine Generator Using Matlab Simulink. Int. J. Enhanc. Res. Sci. Technol. Eng. 2016, 5, 243–254. [Google Scholar]
- Fazylova, A.; Iliev, T.; Stoyanov, I.; Siemens, E. Height Control System for Wind Turbines Based on Critical Wind Speed Calculation. Appl. Sci. 2024, 14, 9802. [Google Scholar] [CrossRef]
- Floors, R.; Nielsen, M. Estimation Air Density Using Observations and Re-Analysis Outputs for Wind Energy Purposes. Energies 2019, 12, 2038. [Google Scholar] [CrossRef]
- Fazylova, A.; Iliev, T.; Balbayev, G. Development of a Monitoring System for the State of the Main Components of the Wind Turbine. J. Electr. Electron. Eng. 2022, 15, 27–32. [Google Scholar]
- Qiu, Y.; Zhang, W.; Cao, M.; Feng, Y.; Infield, D. An Electro-Thermal Analysis of a Variable-Speed Doubly-Fed Induction Generator in a Wind Turbine. Energies 2015, 8, 3386–3402. [Google Scholar] [CrossRef]
- Sheng, Z.; Wang, D.; Fu, J.; Hu, J. A Computationally Efficient Spatial Online Temperature Prediction Method for PM Machines. IEEE Trans. Ind. Electron. 2022, 69, 10904–10914. [Google Scholar] [CrossRef]
- Yu, B.; Zhang, S.; Yan, J.; Cheng, L.; Zheng, P. Thermal Analysis of a Novel Cylindrical Transverse-Flux Permanent-Magnet Linear Machine. Energies 2015, 8, 7874–7896. [Google Scholar] [CrossRef]
- Taras, P.; Nilifard, R.; Zhu, Z.Q.; Azar, Z. Cooling Techniques in Direct-Drive Generators for Wind Power Application. Energies 2022, 15, 5986. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).