Abstract
n-Pentanol, a promising biofuel, can reduce greenhouse gas emissions while remaining compatible with internal combustion engines. We present a reduced kinetic mechanism comprising 66 species and 292 reactions that captures both high- and low-temperature ignition and flame propagation dynamics for this fuel. The mechanism, developed by integrating a detailed n-pentanol sub-mechanism with the San Diego mechanism and applying sensitivity and steady-state approximations criteria as reduction strategies, accurately reproduces key phenomena, including the negative temperature coefficient behavior (NTC). Validation against experimental data for ignition delay times, laminar flame speeds, and speciation measurements in a jet-stirred reactor confirms its predictive capability across a wide range of conditions.
1. Introduction
Global energy demand, primarily met by fossil fuels, has triggered an unprecedented climate crisis due to greenhouse gas emissions [1,2]. This has made the shift to alternative, sustainable energy sources imperative. Biofuels such as n-pentanol [3,4] are promising due to their ability to reduce pollutant emissions and their compatibility with internal combustion engines [5,6]. Consequently, a thorough understanding of combustion processes is essential, with a central focus on reaction mechanisms that detail the elementary steps from fuel breakdown to product formation. While detailed mechanisms are comprehensive, they are computationally demanding; therefore, reduced kinetic models, which simplify the system to key species and reactions, offer enhanced efficiency for numerical simulations [7,8]. Significant progress in developing detailed [9,10,11,12,13,14,15] and reduced [16,17,18] mechanisms for n-pentanol combustion has been made over the past decade, yet gaps remain, especially under low-temperature combustion conditions relevant to engine operations. This study addresses these gaps by developing a reduced kinetic mechanism validated against experimental data for ignition delay times (IDT), laminar flame speeds (LFS), and speciation measurements in a jet-stirred reactor (JSR). To our knowledge, no reduced mechanism simultaneously captures both high- and low-temperature ignition as well as flame propagation dynamics across all test conditions for n-pentanol/air mixtures presented herein.
2. Method: Development of the Reduced Reaction Model
In this study, we developed a reduced kinetic mechanism to model high- and low-temperature ignition and flame behavior in n-pentanol/air mixtures. The San Diego Mechanism (SD Mech) [19], comprising 57 species and 267 reactions, was considered as the base framework due to its robustness in describing combustion phenomena of hydrogen and C1–C4 alkanes. A comprehensive literature review was conducted to identify the key species and reactions relevant to the high- and low-temperature combustion chemistry of n-pentanol. These species and reactions were extracted from detailed mechanisms [10,11,15] and integrated into the SD Mech, resulting in a semi-detailed mechanism with 249 species and 882 reactions (Figure 1).
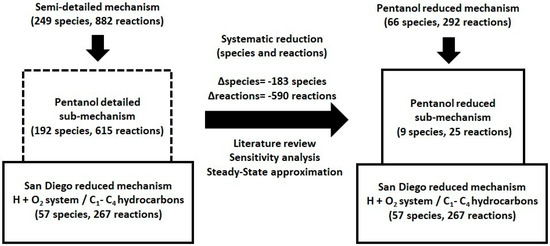
Figure 1.
Development process of a reduced kinetic mechanism for high- and low-temperature ignition and flames of n-pentanol.
This mechanism was systematically reduced using sensitivity and steady-state approximation criteria. In this process, priority is given to removing species over eliminating reactions, since eliminating species directly reduces the number of conservation equations (mass and energy) that must be solved. The steady-state approximation (SSA) is a reaction mechanism simplification method in which it is assumed that, for certain intermediate species present at very low concentrations, the rate of production is approximately equal to the rate of removal , so that their effective concentration remains constant throughout the reaction, thereby reducing the system of conservation equations and facilitating its solution [7].
The final version includes 66 species and 292 reactions, with 9 species and 25 reactions specifically related to n-pentanol. Of these reactions, sixteen correspond to high-temperature chemistry (T ≥ 1000 K), while the remaining nine are associated with low-temperature chemistry (T < 1000 K). Kinetic parameters and rate constants were taken from the literature [10,11,15]. One of the present study’s authors has successfully employed this method [20,21,22,23], achieving precision and alignment with experimental data. The development of the kinetic model and the simulations were conducted using the FlameMaster computational code Version 4.0.0 [24], and the mechanism was validated against a wide range of experimental data [10,11,12,13,15,25,26,27] (Table 1).

Table 1.
Experimental studies on IDT, LFS, and speciation measurements in a JSR for n-pentanol simulated in the present study.
In a previous study [28], we proposed a reduced mechanism for high-temperature ignition and flame propagation in n-pentanol, incorporating seven species and fifteen reactions based on [10,11], including the hydroxypentyl radicals C5H10OH-11 and C5H10OH-13. In the present work, we have also considered the hydroxypentyl radical C5H10OH-14, as reported in [15], which is significant for modeling low-temperature pathways. In the new kinetic model developed herein, the set of nine chemical species ultimately coupled to the SD Mech includes n-pentanol, C5H11OH; the hydroxypentyl radicals C5H10OH-11, C5H10OH-13, and C5H10OH-14; pentanal, PC4H9CHO; the hydroperoxy-alkyl radicals C5H9OH-3OOH-1 and C5H9OH-4OOH-2; and the hydroxy-ketohydroperoxides (hydroxy-KHP) C5OHKET3-1 and C5OHKET4-2.
The reactions associated with n-pentanol chemistry in the reduced sub mechanism developed in this research are described below. The reactions C5H11OH(+M)↔PC4H9+CH2OH(+M) and C5H11OH↔CH2CH2OH+N-C3H7 capture the thermal decomposition of the fuel at high temperature (T > 1000 K), essential for ignition and laminar flame speed. The attack of H, OH, and HO2 radicals on the fuel causes hydrogen abstractions via homolytic C–H bond cleavages, producing the hydroxypentyl radicals C5H10OH-11, C5H10OH-13, and C5H10OH-14, whose relevance is detailed in the following paragraphs and in the sensitivity analysis of Section 3 (Results and Discussion) in this work. The reaction C5H11OH+O2↔C5H10OH-11+HO2 represents the fundamental oxidative step common to all fuels [29,30]. The α-hydroxypentyl radical (C5H10OH-11) decomposes via C5H10OH-11↔CH3CHO+N-C3H7, generating acetaldehyde and propyl radical; this pathway influences ignition at high temperature and flame propagation. Previous studies [13,14,17,18,31] indicate that reaction pathways from the α-carbon of n-pentanol predominantly lead to HO2 and aldehydes, suppressing low-temperature reactivity, as the generated aldehyde follows chain-propagation rather than branching pathways. In n-pentanol, this occurs when the C5H10OH-11 radical reacts with O2 to form pentanal (PC4H4CHO) and HO2. The resulting pentanal reacts with OH and HO2, impacting ignition at both high and low temperatures due to its significant heat contribution. Additionally, the pyrolysis reaction C5H10OH-13↔C4H8+CH2OH delays ignition in the high-temperature regime. Conversely, low-temperature branching pathways are initiated by the first O2 addition to C5H10OH-13 and C5H10OH-14, forming peroxy radicals (RO2), which isomerize to hydroperoxy-alkyl radicals (QOOH: C5H9OH-3OOH-1 and C5H9OH-4OOH-2). These sequences were simplified using the SSA, represented as C5H10OH-13+O2↔C5H9OH-3OOH-1 and C5H10OH-14+O2↔C5H9OH-4OOH-2. A second O2 addition produces peroxy-hydroperoxy-alkyl radicals (O2QOOH), whose decomposition releases OH and forms the hydroxy-ketohydroperoxides C5OHKET3-1 and C5OHKET4-2. These reactions were also simplified via SSA, expressed as C5H9OH-3OOH-1+O2↔C5OHKET3-1+OH and C5H9OH-4OOH-2+O2↔C5OHKET4-2+OH. Subsequent decomposition of these compounds releases additional OH radicals, terminating the branching pathways. At low temperature, oxidation follows inhibitory and propagation pathways, limiting the second O2 addition and branching. The main competing branching pathways, besides pentanal formation as described, include H2O elimination from C5H9OH-3OOH-1 (C5H9OH-3OOH-1↔HCO+C2H4+CH3CHO+H2O), as well as the reactions C5H9OH-3OOH-1+O2↔CH3CHO+HCO+C2H4+OH+HO2 and C5H9OH-4OOH-2↔CH2CO+C3H6+H2O+OH, which generate OH/HO2 and OH/H2O, respectively, alongside carbon chain cleavage products.
Conventional development of reduced kinetic mechanisms often relies on specialized software to automate the simplification process. While these tools offer efficiency and have been extensively validated, they tend to centralize species- and reaction-selection decisions within opaque algorithms, effectively creating a “black box”. In contrast, the method presented here, applied by our research team with excellent results [20,21,22,23,28], systematically documents every reduction step, ensuring that the researcher retains full control over all decisions. This approach integrates the computational power of specialized software (in our case, FlameMaster [24] as a tool to perform the simulations) with the traceability of scientific judgment. Our methodology delivers three key contributions that distinguish it from conventional reduction approaches:
- Standardized base mechanism: The SD Mech is always taken as the base reduced kinetic model, thus streamlining and expediting the integration of any new fuel.
- Stepped, traceable protocol: A rigorous literature review, targeted identification and selection of chemical species and reactions, integration into a semi-detailed mechanism, and stepwise reduction with continuous experimental validation enable the researcher to control each stage of the process.
- Expanded versatility: The resulting reduced mechanisms accurately reproduce the combustion of a fuel and its mixtures with other species included in the SD Mech, broadening their applicability.
3. Results and Discussion
It is essential that a combustion mechanism reliably reproduces both low- and high-temperature ignition behavior as well as laminar flame speeds across a broad spectrum of experimental and operational conditions to be regarded as robust and widely applicable. Ignition delay time and laminar flame speed are critical validation metrics for chemical kinetic models, as they directly reflect the reactivity of both fossil fuels and biofuels [8].
The IDT is the interval a given fuel–air mixture requires to begin oxidizing and releasing heat under specific pressure and temperature conditions [7]. This measure is crucial in internal combustion engines, since it governs phenomena such as preignition, knock, and super-knock [5]. For typical fuels, ignition delay times can vary from microseconds at high temperatures to several seconds at lower temperatures [8].
Figure 2 compares the experimental data [25] with the simulated IDTs obtained using the reduced mechanism developed in this work for a 0.50% n-pentanol mixture at 1.0 atm and equivalence ratios (ϕ) of 0.25, 0.50, and 1.0 under high-temperature conditions (T > 1000 K). The simplified model accurately reproduces the experimental trends, showing excellent agreement at ϕ = 1.0 and only minor discrepancies for lean mixtures (ϕ = 0.50 and 0.25). Figure 2b displays the ignition delay times (IDTs) for n-pentanol/air mixtures under three distinct pressure and equivalence ratio conditions: 9.0 bar, ϕ = 1.0; 15.0 bar, ϕ = 0.5; and 30.0 atm, ϕ = 2.0. These conditions were selected to validate the versatility and precision of the model in capturing key low- and high-temperature ignition phenomena across diverse experimental and operational scenarios [10,11,15].
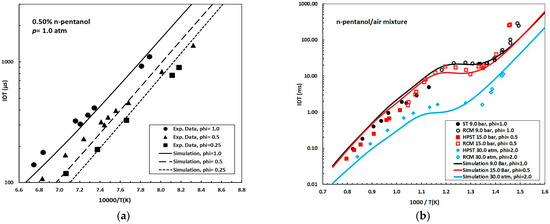
Figure 2.
(a) Experimental data (symbols) [25] and simulation (solid and dashed lines) of ignition delay time (IDT, in microseconds, μs) for mixtures of n-pentanol/air, 0.50% n-pentanol, p = 1.0 atm; ϕ = 1.0, 0.5, and 0.25; (b) experimental data (symbols) and simulation (lines) of ignition delay time (IDT, in milliseconds, ms) for mixtures of n-pentanol/air; p = 9.0 bar, 15.0 bar, and 30.0 atm; ϕ = 1.0, 0.5, and 2.0, respectively. Experimental data for 9.0 bar: [10,11]. Experimental data for 15.0 bar and 30.0 atm: [15].
- Interpreting the plot from right to left (where increasing 1000/T values correspond to lower temperatures), three different behavioral regions are identified:
- (1)
- Low-Temperature Regime (T ≲ 770 K, 1000/T ≳ 1.30 K−1): IDTs decrease continuously with rising temperature, transitioning from hundreds of milliseconds at the rightmost edge of the curve to tens of milliseconds near the onset of the negative temperature coefficient (NTC) region.
- (2)
- NTC Region (≈770–830 K, 1000/T ≈ 1.30–1.20 K−1): Notably, the model successfully predicts the NTC behavior. The NTC phenomenon is manifested by an increase in IDT with rising temperature, and is ascribed to the competitive interplay among chain-propagation, branching, and chain-inhibition pathways involving alkyl-peroxy (RO2) and hydroperoxy-alkyl radicals (QOOH) under low-temperature conditions. The accurate simulation of NTC behavior is critical, as it directly influences ignition stability and reactivity. In n-pentanol, the first linear alcohol reported to exhibit NTC behavior [10,11,15,29], this effect remains modest, indicating a borderline case compared to higher lineal alcohols where NTC is more pronounced [29].
- (3)
- High-Temperature Regime (T ≳ 1000 K, 1000/T ≲ 1.00 K−1): As temperature rises further, IDTs decrease sharply, reaching values on the order of 0.01–0.3 ms.
Across the evaluated conditions, the reduced model successfully captures the pressure-dependent shift in the NTC region to higher temperatures, from 770–830 K at 9 bar to ≈830–910 K at 15 bar and 30 atm, and demonstrates progressive attenuation of the NTC trough at elevated pressures, with the slope approaching zero. This observation is consistent with the findings reported in [15], which show that NTC effects diminish with increasing pressure and become negligible at 30.0 bar. Furthermore, the NTC effect is slightly more pronounced under fuel-lean conditions (ϕ < 1.0) compared to stoichiometric or fuel-rich mixtures.
To evaluate combustion mechanisms, the choice of uncertainty metric must align with the nature of the data under study. In this work, the predictive capability of the reduced kinetic mechanism for n-pentanol ignition delay times was assessed using the Logarithmic Willmott Concordance Index () [30], which captures both bias and dispersion in a single measure:
where denotes the mean of the logarithmic experimental IDTs. The superscripts “exp” and “sim” refer to experimental measurements and simulation results, respectively. Bounded between 0 and 1, this index simultaneously evaluates trend agreement, including minima, maxima, and characteristic transitions, and relative magnitude, preserving consistency across orders of magnitude. By operating in logarithmic space, stabilizes the variance in ignition delay times, which span from tenths to hundreds of milliseconds, ensuring that no thermal regime disproportionately influences the assessment. This approach is particularly pertinent for ignition data, where underlying physicochemical processes yield substantial heterogeneity across temperature regimes.
The uncertainty analysis encompassed 62 experimental–simulation pairs across the full thermal range at both high and low temperatures: 25 pairs at 9 bar (ϕ = 1.0), 24 pairs at 15 bar (ϕ = 0.5), and 13 pairs at 30 atm (ϕ = 2.0). Within this dataset, ranged from 0.96 to 0.98, indicating that deviations remain within typical experimental uncertainty bounds.
Condition-specific analyses further illustrate the robustness of the reduced mechanism: at 9 bar and ϕ = 1.0, it accurately reproduces both the characteristic trough and peak that delimit the NTC region; at 15 bar and ϕ = 0.5, the agreement remains strong, although the mechanism slightly underpredicts the depth of the NTC region. At 30 atm and ϕ = 2.0, the mechanism accurately reproduces the flat IDT behavior within the NTC regime but tends to underestimate ignition delays at high temperatures, likely attributable to enhanced radical recombination and termination pathways under high-pressure, fuel-rich conditions.
Together, these findings demonstrate that the proposed reduced kinetic mechanism delivers reliable predictive performance across low-, intermediate- (NTC), and high-temperature ignition regimes over a broad range of pressures and equivalence ratios. Its ability to reproduce both trend and magnitude in logarithmic space confirms its physical and chemical fidelity, outperforming conventional error metrics that do not accommodate the inherent heteroscedasticity of ignition data.
Laminar flame speed denotes the propagation rate of unburned gases perpendicular to the flame front [13]. It is essential for estimating emissions from air–fuel mixtures under varying conditions and provides insight into fuel reactivity, heat release, and thermal diffusivity. The laminar flame speed of a given fuel–oxidizer mixture depends on the initial pressure, the temperature of the unburned mixture, and the equivalence ratio [13]. For flame analysis, experimental data from [12,13,26] were used for validation, and laminar flame speeds were predicted without accounting for thermal diffusion effects.
Figure 3 illustrates the results of simulations conducted with the reduced mechanism proposed in this study, showing laminar flame speeds under various conditions alongside the corresponding experimental measurements [12,13,26]. Unlike ignition delay times, which can span several orders of magnitude, laminar flame speeds exhibit relatively bounded variations with respect to parameters such as temperature, pressure, and equivalence ratio. Consequently, traditional statistical metrics, namely RMSE (root mean square error), MAPE (mean absolute percentage error), and R2 (coefficient of determination), are well suited to quantify deviations between experimental and model-predicted values without requiring additional transformations. In this study, the reduced kinetic mechanism was assessed against 85 experimental laminar flame speed measurements covering pressures ranging from 0.10 to 0.75 MPa and equivalence ratios of ϕ = 0.6–1.8. The RMSE ranged from 1.31 cm/s at higher pressures to 4.87 cm/s at 0.10 MPa (overall average: 3.12 cm/s), and the MAPE varied between 2.9% and 9.2% (mean: 5.0%).
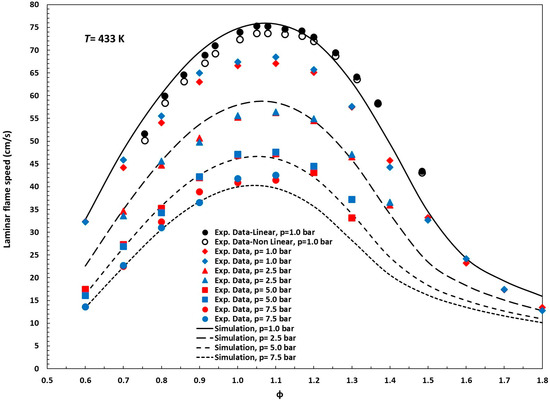
Figure 3.
Experimental data (symbols) and simulation (solid and dashed lines) for laminar flame speed, n-pentanol/air mixtures, T = 433 K; p = 1.0, 2.5, 5.0, and 7.5 bar. Symbols: black, reference [13]; red, reference [12]; blue, reference [26].
The calculated R2 value ranges from 0.92 to 0.98, meaning that 92–98% of the variance in the experimental flame speeds is captured by the simulations (mean 97%), indicating excellent overall agreement. Moreover, the increase to R2 ≥ 0.98 at pressures ≥ 0.25 MPa shows that under these conditions, the model explains virtually all of the observed variability in flame speed. Altogether, these results confirm the mechanism’s high predictive accuracy for laminar flame speeds across a wide range of operating conditions.
Discrepancies between our LFS simulations and the experimental data reported by Li et al. [15,30] may stem from variations in the O2 content of the air used during the experiments. Nativel et al. [13] noted that Li et al. [12,26] likely employed air with an oxygen concentration below 21.0% (closer to 20.0%), although this was not explicitly stated. We analyzed this issue in our previous work [28] and confirmed that the hypothesis proposed by Nativel et al. [13] is highly plausible.
The jet-stirred reactor is an indispensable experimental tool for investigating fuel reactivity across low- and high-temperature regimes. The proposed kinetic mechanism was validated against speciation measurements in a JSR reported by Pelucchi et al. [27], carried out at an equivalence ratio (ϕ) of 1.0, a pressure of 1.07 bar, and a residence time (τ) of 2.0 s. Figure 4 shows the simulations conducted using the Perfectly Stirred Reactor (PSR) model within the FlameMaster code [24,27].
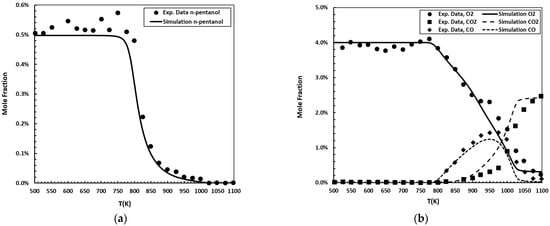
Figure 4.
n-Pentanol oxidation in a JSR at 1.07 bar, ϕ = 1.0, and τ = 2.0 s. Initial mole fractions: 0.5% for the fuel; 4.0% for O2. Experimental data [27] (symbols) are compared to simulations (solid and dashed lines): (a) n-pentanol molar fraction as a function of temperature; (b) O2, CO2, and CO molar fractions as a function of temperature.
To conduct an uncertainty analysis in studies of this nature, at a minimum the Willmott’s index and the coefficient of variation of RMSE () are required, as they collectively address key aspects of multi-order-of-magnitude data, trend fidelity, and absolute error magnitude. Willmott’s index quantifies agreement in curve shape, ensuring that peaks, troughs, and transitional features are accurately captured. [31] is defined as follows:
where and denote the experimental and simulated concentrations of species , respectively, and is the mean experimental concentration, which expresses absolute deviations relative to each species’ scale by normalizing the root mean square error to the average measured value. Together, these metrics provide a balanced, rigorous validation of a reduced mechanism’s predictive performance.
The evaluation of the reduced mechanism demonstrates robust performance in predicting n-pentanol and O2 concentrations in the JSR. The calculated Willmott’s index of 0.97 for both species confirms that the simulated trends exhibit a high degree of agreement with experimental measurements. The values indicated low normalized absolute errors, with deviations of 15.1% for n-pentanol and 8.9% for O2, representing only a small fraction of the respective mean experimental concentrations. These results are based on 24 experimental–simulation data pairs for n-pentanol and 25 for O2. Taken together, the metrics confirm that the mechanism reliably reproduces both the magnitude of and trend in the measured profiles for these species.
Figure 5a,b compare the simulations obtained with the reduced mechanism proposed in this study against the latest detailed [15] and reduced [18] mechanisms reported in the literature for n-pentanol.
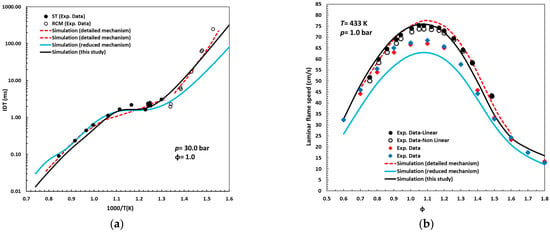
Figure 5.
Comparison of the simulations performed with the reduced mechanism presented in this study to those from the latest detailed (red dashed lines) [15] and reduced (blue solid lines) [18] mechanisms reported in the literature for n-pentanol, as well as to experimental data for (a) ignition delay times (ST and RCM) [15] and (b) laminar flame speeds. Symbols: black, reference [13]; red, reference [12]; blue, reference [26].
Under the conditions of Figure 5a, the detailed mechanism, composed of 612 species and 3636 reactions, exhibits high agreement with experimental data, with only minor deviations. This characteristic justified its selection as the primary reference for extracting the reactions associated with n-pentanol chemistry, which, through the reduction methodology described earlier, enabled the construction of the simplified kinetic scheme developed in this work.
The new simplified model, comprising 66 species and 292 reactions, demonstrates predictive accuracy comparable to that of the detailed mechanism, reproducing the low-temperature kinetics with high degree fidelity, capturing the valley and peak of the NTC region, and accurately modeling the high-temperature regime. In contrast, the reduced mechanism reported in [18] shows significant deviations in both the low- and high-temperature regions, in that order of importance.
Regarding laminar flame speeds (Figure 5b), the novel reduced mechanism achieves agreement with experimental measurements on par with the detailed scheme. Notably, it surpasses the predictive capability of the detailed mechanism under rich mixture conditions (ϕ > 1.0), where the latter tends to overestimate flame speeds. Conversely, the reduced mechanism of [18] consistently underestimates the experimental data by 5–10 cm/s, with the discrepancy most pronounced for equivalence ratios between 0.9 and 1.3. Collectively, these results confirm that the predictive capability of the proposed reduced mechanism is analogous to that of the detailed model, but with only a fraction of its complexity.
Sensitivity analysis (SA), a standard technique to quantify how individual input parameters influence model outputs [7], was employed here to validate the incorporation of the hydroxypentyl radicals C5H10OH-11, C5H10OH-13, and C5H10OH-14, as well as their associated reactions into the proposed reduced kinetic mechanism across both low- and high-temperature regimes. In this framework, the sensitivity coefficient, , measures the change in an output variable , in this case, ignition delay time, resulting from a finite perturbation in a selected parameter , while all other parameters remain fixed. To enable direct comparison across parameters of different scales, coefficients are normalized to a dimensionless form [7]. Normalized sensitivity coefficients,, were obtained by doubling the pre-exponential factor ,in the modified Arrhenius expression for each reaction in the reduced mechanism. A positive indicates that increasing a reaction’s reactivity lengthens the IDT, whereas a negative signifies a shortening of the IDT. All computations were performed with the FlameMaster code [28] at 9.0 bar and an equivalence ratio of 1.0, conditions under which n-pentanol exhibits clear NTC behavior [10,11,15,29,30]. Sensitivity coefficients were evaluated at 620 K (low-temperature regime), 770 K (the “trough” marking NTC onset), 803 K (the “peak” marking NTC end), and 1050 K (high-temperature regime) (see Figure 2b).
Figure 6 presents the twenty reactions exhibiting the highest absolute normalized sensitivity coefficients at each of the temperatures considered. At 620 K, 770 K, and 830 K, the most influential processes are hydrogen abstraction reactions of n-pentanol by OH and HO2 radicals, yielding the hydroxypentyl radicals C5H10OH-11, C5H10OH-13, and C5H10OH-14. The reaction C5H11OH+OHC5H10OH-11+H2O exhibits the highest positive sensitivity, confirming that its inclusion is critical to capturing IDT lengthening in the low-temperature regime, whereas the reactions C5H11OH+OHC5H10OH-13+H2O and C5H11OH+OHC5H10OH-14+H2O display negative sensitivities. Additional low-temperature branching pathways, namely, second O2 additions to C5H10OH-13 (C5H9OH-3OOH-1+O2C5OHKET3-1+OH) and C5H10OH-14 (C5H9OH-4OOH-2+O2C5OHKET4-2+OH), hydroxy-KHP decompositions (C5OHKET3-1CH2CO+C2H5+CO2+H2+OH; C5OHKET4-22CH2CO+CH3+H2O+OH), and pentanal-related reactions (its formation reaction through the addition of O2 to C5H10OH-11 and its decomposition reactions with OH and HO2), also contribute substantially to the IDT prediction. At 1050 K, the sensitivity landscape shifts:
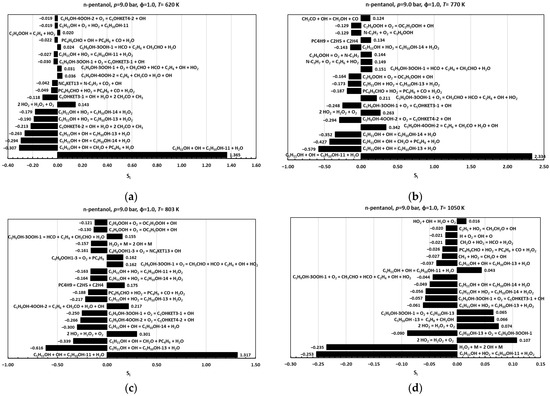
Figure 6.
Sensitivity coefficients for the ignition of n-pentanol/air mixtures at p = 9.0 bar, ϕ = 1.0: (a) 620 K; (b) 770 K; (c) 803 K; (d) 1050 K.
HO2 abstraction of n-pentanol to form C5H10OH-11 becomes the most sensitive reaction, exhibiting a negative coefficient, and HO2-mediated abstractions generally outweigh those mediated by OH. Moreover, the first O2 addition to C5H10OH-13 (C5H10OH-13+O2C5H9OH-3OOH-1), as well as its pyrolysis (C5H10OH-13C4H8+CH2OH), and key chain-branching steps involving H2O2 (2HO2H2O2+O2; H2O2+M2OH+M) gain prominence. Finally, regarding the comparative analysis of sensitivity coefficients for ignition, it is noteworthy that their absolute values exhibit a significant decreasing trend as temperature increases beyond 700–800 K. Together, these results confirm that the hydroxypentyl radicals C5H10OH-11, C5H10OH-13, and C5H10OH-14 and their associated high- and low-temperature reactions are indispensable for accurately modeling ignition delay across all relevant temperature regimes. Omission of these species or pathways would significantly impair the mechanism’s predictive capability.
4. Conclusions
In this work, a reduced kinetic mechanism for n-pentanol combustion was developed and validated, consisting of 66 species and 292 reactions. This model was derived from the San Diego mechanism, incorporating species and reactions specific to n-pentanol from a detailed mechanism and applying a systematic reduction process based on sensitivity and steady-state approximation criteria. This kinetic scheme accurately captures key ignition and combustion phenomena in both high- and low-temperature regimes, such as NTC behavior, and demonstrates high predictive accuracy against experimental data across a wide range of conditions. Consequently, this reduced mechanism is useful for practical applications in combustion system modeling, such as engine design and optimization, especially when detailed mechanisms would be too time-consuming to implement.
Author Contributions
Conceptualization, J.C.P.; methodology, J.C.P.; validation, J.T.-C.; formal analysis, J.T.-C.; investigation, J.T.-C.; resources, A.Z.; writing—original draft, J.T.-C.; writing—review and editing, J.C.P.; supervision, J.C.P. and A.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were generated in this research.
Acknowledgments
The authors acknowledge the support provided by Tecnológico de Monterrey, México.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SD Mech | San Diego mechanism |
| IDT | Ignition delay time |
| LFS | Laminar flame speed |
| KHP | Ketohydroperoxide |
| NTC | Negative temperature coefficient |
| ST | Shock tube |
| HPST | High pressure shock tube |
| RCM | Rapid compression machine |
| JSR | Jet-stirred reactor |
| PSR | Perfectly Stirred Reactor |
| SA | Sensitivity analysis |
| RMSE | Root mean square error |
| MAPE | Mean absolute percentage error |
| R2 | Coefficient of determination |
| CV-RMSE | Coefficient of variation of RMSE |
References
- Climate Change 2021: The Physical Science Basis. Available online: https://www.ipcc.ch/report/ar6/wg1 (accessed on 23 March 2025).
- Renewable Energy Policy Network for the 21st Century (REN 21). Available online: https://www.ren21.net/reports/global-status-report/ (accessed on 23 March 2025).
- Kremer, F.; Blank, L.M.; Jones, P.R.; Akhtar, M.K. A comparison of the microbial production and combustion characteristics of three alcohol biofuels: Ethanol, 1-butanol, and 1-octanol. Front. Bioeng. Biotechnol. 2015, 3, 112. [Google Scholar] [CrossRef]
- Babu, V.M.; Murthy, M.K.; Rao, A.P.G. Butanol and pentanol: The promising biofuels for CI engines—A review. Renew. Sustain. Energy Rev. 2017, 78, 1068–1188. [Google Scholar] [CrossRef]
- Nour, M.; Attia, A.M.A.; Nada, S.A. Improvement of CI engine combustion and performance running on ternary blends of higher alcohol (Pentanol and Octanol)/hydrous ethanol/diesel. Fuel 2019, 251, 10–22. [Google Scholar] [CrossRef]
- Rajesh Kumar, B.; Saravanan, S. Effects of iso-butanol/diesel and n-pentanol/diesel blends on performance and emissions of a diesel engine under premixed LTC (low-temperature combustion) mode. Fuel 2016, 170, 49–59. [Google Scholar] [CrossRef]
- Turányi, T.; Tomlin, A.S. Analysis of Kinetic Reaction Mechanism; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Westbrook, C.; Heufer, K.A.; Wildenberg, A. Key Chemical Kinetic Steps in Reaction Mechanisms for Fuels from Biomass: A Perspective. Energy Fuels 2021, 35, 15339–15359. [Google Scholar] [CrossRef]
- Togbé, C.; Halter, F.; Foucher, F.; Mounaim-Rousselle, C.; Dagaut, P. Experimental and detailed kinetic modeling study of 1-pentanol oxidation in a JSR and combustion in a bomb. Proc. Combust. Inst. 2011, 33, 367–374. [Google Scholar] [CrossRef]
- Heufer, K.A.; Sarathy, S.M.; Curran, H.J.; Davis, A.C.; Westbrook, C.K.; Pitz, W.J. Detailed kinetic modeling study of n-pentanol oxidation. Energy Fuels 2012, 26, 6678–6685. [Google Scholar] [CrossRef]
- Heufer, K.A.; Bugler, J.; Curran, H.J. A comparison of longer alkane and alcohol ignition including new experimental results for n-pentanol and n-hexanol. Proc. Combust. Inst. 2013, 34, 511–518. [Google Scholar] [CrossRef]
- Li, Q.; Hu, E.; Zhang, X.; Cheng, Y.; Huang, Z. Laminar flame speed and flame instabilities of pentanol isomer-air mixtures at elevated temperatures and pressures. Energy Fuels 2013, 27, 1141–1150. [Google Scholar] [CrossRef]
- Nativel, D.; Pelucchi, M.; Frassoldati, A.; Comandini, A.; Cuoci, A.; Ranzi, E.; Chaumeix, N.; Faravelli, T. Laminar flame speed of pentanol isomers: An experimental and modeling study. Combust. Flame 2016, 166, 1–18. [Google Scholar] [CrossRef]
- Pelucchi, M.; Namysl, S.; Ranzi, E.; Rodríguez, A.; Rizzo, C.; Somers, K.P.; Zhang, Y.; Herbinet, O.; Curran, H.J.; Battin-Leclerc, F.; et al. Combustion of n-C3-C6 Linear Alcohols: An Experimental and Kinetic Modeling Study. Part I: Reactions Classes, Rate Rutes, Model Lumping and Validation. Energy Fuels 2020, 34, 14688–14707. [Google Scholar] [CrossRef]
- Chatterjee, T.; Saggese, C.; Dong, S.; Patel, V.; Lockwood, K.S.; Curran, H.J.; Labbe, N.J.; Wagnon, S.W.; Pitz, W.J. Experimental and kinetic modeling study of the low-temperature and high-pressure combustion chemistry of straight chain pentanol isomers: 1-, 2- and 3-Pentanol. Proc. Combust. Inst. 2023, 39, 265. [Google Scholar] [CrossRef]
- Liu, X.; Wang, H.; Zheng, Z.; Liu, J.; Reitz, R.D.; Yao, M. Development of a combined reduced primary reference fuel-alcohols (methanol/ethanol/propanols/butanols/n-pentanol) mechanism for engine applications. Energy 2016, 114, 542–558. [Google Scholar] [CrossRef]
- Li, S.; Zhang, C.; Jing, Z.; Li, Y.; Yin, P.; Cai, P.; Lu, A. Development of a reduced chemical reaction mechanism for n-Pentanol based on combined reduction methods and genetic algorithm. ACS Omega 2021, 6, 6448–6459. [Google Scholar] [CrossRef] [PubMed]
- Chang, Y.; Jia, M.; Huang, S.; Zhang, H.; Cai, L. Development of skeletal oxidation mechanisms for linear alcohols from C4 to C10 based upon reaction rate rules. Combust. Flame 2022, 245, 112351. [Google Scholar] [CrossRef]
- Chemical-Kinetic Mechanisms for Combustion Applications. Available online: https://web.eng.ucsd.edu/mae/groups/combustion/mechanism.html (accessed on 2 April 2025).
- Prince, J.C.; Treviño, C.; Williams, F.A. A reduced reaction mechanism for the combustion of n-butane. Combust. Flame 2017, 175, 27–33. [Google Scholar] [CrossRef]
- Prince, J.C.; Williams, F.A.; Ovando, G.E. A short mechanism for the low-temperature ignition of n-heptane at high pressures. Fuel 2015, 149, 138–142. [Google Scholar] [CrossRef]
- Prince, J.C.; Williams, F.A. A short reaction mechanism for the combustion of dimethyl-ether. Combust. Flame 2015, 162, 3589–3595. [Google Scholar] [CrossRef]
- Díaz-González, M.; Treviño, C.; Prince, J.C. A Reduced Kinetic Mechanism for the Combustion of n-Butanol. Energy Fuels 2018, 32, 867–874. [Google Scholar] [CrossRef]
- Pitsch, H. FlameMaster: A C++ Computer Program for 0D Combustion and 1D Laminar Flame Calculations. Available online: https://web.stanford.edu/group/pitsch/FlameMaster.htm (accessed on 15 January 2025).
- Tang, C.; Wei, L.; Man, X.; Zhang, J.; Huang, Z.; Law, C.K. High-temperature ignition delay times of C5 primary alcohols. Combust. Flame 2013, 160, 520–529. [Google Scholar] [CrossRef]
- Li, Q.; Tang, C.; Cheng, Y.; Guan, L.; Huang, Z. Laminar Flame Speeds and Kinetic Modeling of n-Pentanol and Its Isomers. Energy Fuels 2015, 29, 5334–5348. [Google Scholar] [CrossRef]
- Pelucchi, M.; Namysl, S.; Ranzi, E.; Rodríguez, A.; Rizzo, C.; Somers, K.P.; Zhang, Y.; Herbinet, O.; Curran, H.J.; Battin-Leclerc, F.; et al. Combustion of n-C3-C6 Linear Alcohols: An Experimental and Kinetic Modeling Study. Part II: Speciation Measurements in a Jet-Stirred Reactor, Ignition Delay Time Measurements in a Rapid Compression Machine, Model Validation, and Kinetic Analysis. Energy Fuels 2020, 34, 14708–14725. [Google Scholar] [CrossRef] [PubMed]
- Tiburcio-Cortés, J.; Prince, J.C.; Treviño, C. Reduced kinetic mechanism for modeling High-Temperature Ignition and Flames for n-Pentanol. ACS Omega 2024, 9, 38906–38915. [Google Scholar] [CrossRef] [PubMed]
- Cai, L.; Uyngun, Y.; Togbé, C.; Pitsch, H.; Olivier, H.; Dagaut, P.; Sarathy, S.M. An experimental and modeling study of n-octanol combustion. Proceed. Combust. 2015, 35, 419–427. [Google Scholar] [CrossRef]
- Willmott, C.J.; Robenson, S.M.; Matsuura, K. A refined index of model performance. Int. J. Climatol. 2011, 32, 2088–2094. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Koehler, A.B.; Ord, J.K.; Snyder, R.D. Forecasting with Exponential Smoothing. The State Space Approach; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).