Abstract
This paper presents an analysis of the time-dependent response of a spherical container to internal pressure that increases over time. The wall of the container is relatively thin, in the sense that the wall thickness is negligible in comparison to the container’s radius. The wall is composed of three layers. The two surface layers of the wall are identical, i.e., they are made from the same material and have the same thickness. One of the most important features regarding the response of the wall layers is the non-linear creep. The stresses and strains are determined, and their relationships with the parameters of the layers are studied.
1. Introduction
The increasing use of containers with fluids (gases, liquids) under pressure in different technical applications has led to a need for the introduction of new engineering materials for the container walls, as well as the development of reliable methods for analyzing the container’s mechanical response to various loading types and influences [1,2,3,4,5,6,7]. Such analyses are challenging and time-consuming, since many issues must be addressed in detail, and the effects of a variety of factors and technical parameters must be properly assessed.
One of the structural material types with a rapidly expanding field of application is layered materials [8,9,10]. These materials have numerous advantages. As a result, they are replacing homogeneous materials at an increasing rate.
This paper addresses the problem of the response of a spherical container—with a wall made of three layers—to internal uniform pressure that increases over time. Under such pressure, the wall layers undergo non-linear creep. Therefore, the response of the container is time-dependent. An analytical procedure is applied to determine the time-dependent parameters of the stressed and strained states of the layers. This procedure exploits the full symmetry that exists in spherical containers under uniform pressure (due to this symmetry, the meridional and the hoop stresses are the same). The relationship between the stresses and the parameters of the wall layers is also studied.
2. Analysis of the Container Wall Response
A spherical container is shown in Figure 1. The container wall has three layers. The surface layers have the same thickness, . Thus, the thickness of the middle layer of the wall is , where is marked in Figure 1. The thickness of the container wall, , is negligible compared to the container’s radius, . The container is under an internal uniform pressure of intensity, . The pressure intensity increases with time, , according to Equation (1).
where is a parameter. All symbols are summarized in Table A1 in Appendix A.
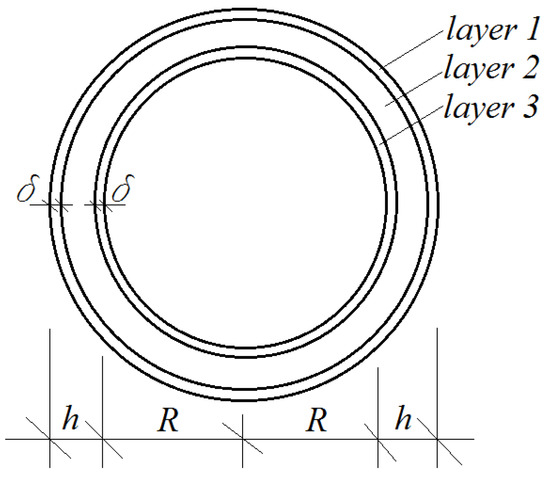
Figure 1.
Schema of the spherical container.
The wall layers behave as viscoelastic bodies under non-linear creep. The creep model is shown in Figure 2.
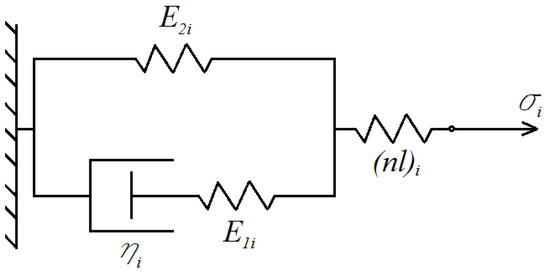 The stress, , in the model is as follows:
where is a parameter. The stress, , in the non-linear spring, , of the model depends on the strain, , according to Equation (3) [11].
where and are material properties. We investigated the response of the model in Figure 2 to the stress, , at initial conditions, , and found the following:
where
The third addend in Equation (4) is found by extracting of from Equation (3). We examined the equilibrium of an element of the container wall and obtained the following:
where
where and are the meridional stresses in the surface and middle layers, and are the hoop stresses in the surface and middle layers of the container, and are the container curvatures radiuses. Due to the full symmetry in the spherical container, we have the following:
Therefore, from Equation (6), one obtains the following:
where and are the stresses in the surface and middle layers.
The stress, , in the model is as follows:
where is a parameter. The stress, , in the non-linear spring, , of the model depends on the strain, , according to Equation (3) [11].
where and are material properties. We investigated the response of the model in Figure 2 to the stress, , at initial conditions, , and found the following:
where
The third addend in Equation (4) is found by extracting of from Equation (3). We examined the equilibrium of an element of the container wall and obtained the following:
where
where and are the meridional stresses in the surface and middle layers, and are the hoop stresses in the surface and middle layers of the container, and are the container curvatures radiuses. Due to the full symmetry in the spherical container, we have the following:
Therefore, from Equation (6), one obtains the following:
where and are the stresses in the surface and middle layers.

Figure 2.
Creep model.
For , from Equation (4), one has the following:
For , from Equation (4),
We determined , and from Equations (14)–(16) by the MatLab 6.5. This was performed using various values of in order to study the creep behavior of the spherical container.
Since Equation (6) has fundamental importance for the accuracy of the current investigation, we checked this equation in the following manner. At the following:
the wall becomes homogeneous. In view of this, at , Equation (6) should transform into the equilibrium equation for thin homogeneous containers. In order to verify this, upon substituting into Equation (6) and simplifying it, one obtains the following equation:
which is the known equation for thin homogeneous containers [12]; this confirms that Equation (6) is right.
Keeping in mind that for spherical containers, , from Equation (16), one can derive the following:
which is also a known equation [12].
One of the possible applications of the above-mentioned approach presented by Equations (14)–(16) is to study the change in the response of the container wall layers to increasing internal pressure over time. This application is very useful, as non-linear creep is incorporated in the equations. The approach can also be applied to study how the stresses in the wall layers depend on certain basic parameters of the container, e.g., the relative thickness of the surface layers and the relationships between the material properties of the surface and middle layers.
The study resulted in the dependencies, graphs of which are shown in Figure 3, Figure 4 and Figure 5. The change in with normalized time is shown in Figure 3. The dependence of the normalized stress in the surface layer of the wall on the relative thickness of the surface layer is shown in Figure 4 for growing ratio. The dependence of the normalized stress in the middle layer of the wall on and ratios is shown in Figure 5.
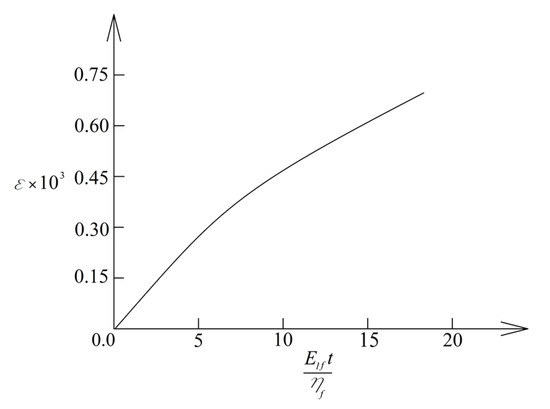
Figure 3.
Change in with normalized time.
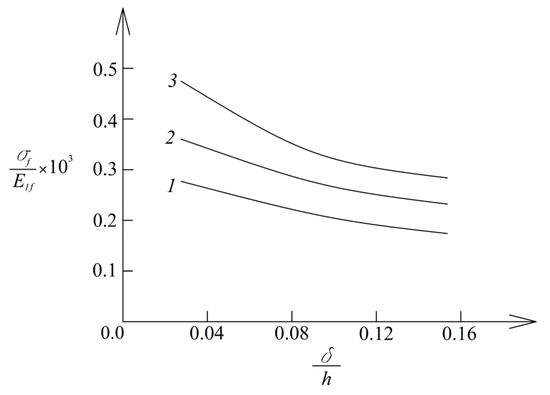
Figure 4.
Dependence of normalized stress in the surface layer of the wall on the relative thickness of the surface layer,
(1—for , 2—for and 3—for ).
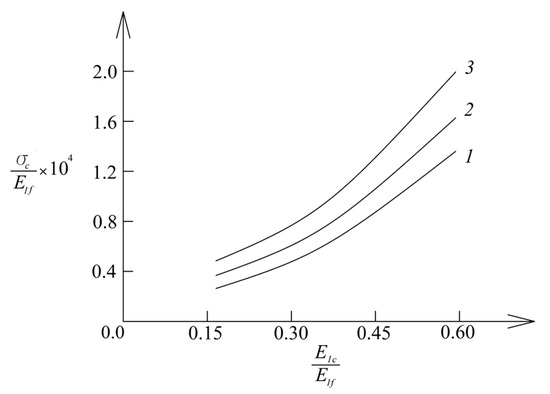
Figure 5.
Dependence of normalized stress in the middle layer of the wall on
ratio (1—for , 2—for and 3—for ).
3. Conclusions
A spherical container subjected to internal pressure that increases over time is analyzed in this study. The container wall consists of three layers that behave as viscoelastic bodies under non-linear creep. The analysis determines the time-dependent wall response in terms of stresses and strains. It is well known in engineering practice that one of the most important questions in the design of containers under internal pressure is how to keep the stresses in the container wall as low as possible. A key conclusion from the current analysis is that the stresses in the surface layers of the container wall can be reduced by increasing the relative thickness of these layers. However, increasing the ratio results in a rise in stresses within the surface layers. Regarding the behavior of the stresses in the middle layer of the container wall, the analysis indicates that the stresses can be reduced by using materials with lower and ratios. Concerning the practical implications and limitations of the model, it should be noted that the model is applicable only to spherical containers with thin walls. The practical applicability of such models can ultimately be proven by nonlinear numerical simulations [13,14].
Funding
Not applicable.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data will be made available upon request.
Conflicts of Interest
The author declares no conflicts of interest.
Appendix A

Table A1.
Symbols and units.
Table A1.
Symbols and units.
| Symbols and Units | ||
|---|---|---|
| E1i—modulus of elasticity of spring 1 [Pa] | E2i—modulus of elasticity of spring 2 [Pa] | h—container wall thickness [m] Hi—material property [1/Pa] |
| Li—material property [1/Pa] t—time [s] δ—wall thickness [m] ρm—curvature radius in meridional plane [m] ρp—curvature radius in hoop plane [m] σc—stress in the middle layer [Pa] | q—internal pressure [Pa] vq—parameter of pressure [Pa/s] ηc—coefficient of viscosity of the middle layer [Pa.s] σf—stress in the surface layer [Pa] σp—hoop stress [Pa] | R—container radius [m] vσi—parameter of the model [Pa/s] ε—strain [-] ηf—coefficient of viscosity of the surface layer [Pa.s] σm—meridional stress [Pa] |
References
- Atkin, R.J.; Fox, N. An Introduction to the Theory of Elasticity; Courier Corporation: North Chelmsford, MA, USA, 2013. [Google Scholar]
- Spencer, A.J.M. Continuum Mechanics; Courier Corporation: North Chelmsford, MA, USA, 2004. [Google Scholar]
- Kachanov, M.L.; Shafiro, B.; Tsukrov, I. Handbook of Elasticity Solutions. Springer Science & Business Media: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Goodier, J.N.; Hodge, P.G., Jr. Elasticity and Plasticity: The Mathematical Theory of Elasticity and the Mathematical Theory of Plasticity; Courier Dover Publications: Garden City, NY, USA, 2016. [Google Scholar]
- Ciarlet, P.G. Mathematical Elasticity: Three-Dimensional Elasticity; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2021. [Google Scholar]
- Avinoam, L. The Nonlinear Theory of Elastic Shells: One Spatial Dimension; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Kružík, M.; Roubíček, T. Mathematical Methods in Continuum Mechanics of Solids; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar]
- Carrera, E. CZ requirements—Models for the two dimensional analysis of multilayered structures. Compos. Struct. 1997, 37, 373–383. [Google Scholar] [CrossRef]
- Clemens, B.M.; Kung, H.; Barnett, S.A. Structure and strength of multilayers. MRS Bull. 1999, 24, 20–26. [Google Scholar] [CrossRef]
- Lu, Y.Y.; Kotoka, R.; Ligda, J.P.; Cao, B.B.; Yarmolenko, S.N.; Schuster, B.E.; Wei, Q. The microstructure and mechanical behavior of Mg/Ti multilayers as a function of individual layer thickness. Acta Mater. 2014, 63, 216–231. [Google Scholar] [CrossRef]
- Lukash, P.A. Fundamentals of Non-Linear Structural Mechanics; Stroiizdat: Moscow, Russia, 1978. [Google Scholar]
- Darkov, A.B.; Shpiro, G.S. Strength of Materials; Vishaya Shkola: Moscow, Russia, 1989. [Google Scholar]
- Wriggers, P. Nonlinear Finite Element Methods; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Kim, N.-H. Introduction to Nonlinear Finite Element Analysis; Springer: New York, NY, USA, 2015. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).