Abstract
In response to the growing prevalence of tariffs as instruments of economic policy and strategic competition, this paper introduces a formal mathematical framework for optimizing counter-tariff strategies. We model the global trade ecosystem as a multi-layered, directed, weighted hypergraph, where vertices represent countries, industries, and subindustries, and hyperedges capture complex trade relationships and supply chain dependencies. The proposed framework employs bilevel optimization techniques to maximize strategic impact on target economies while minimizing self-inflicted economic costs. Through integration of graph theory, spectral analysis, and multilevel optimization methods, we develop a rigorous formalism that enables policymakers to identify optimal counter-tariff portfolios under various constraints. Our model explicitly accounts for industrial interdependencies, where export competitiveness depends on imported inputs, thus providing a more realistic representation of global value chains. Case studies applying our model to historical trade disputes demonstrate its capacity to generate superior strategic outcomes compared to conventional approaches. The framework’s axiomatic foundation allows for rapid recalibration in response to shifting economic conditions and policy objectives.
1. Introduction
In an era marked by geopolitical tensions, economic nationalism, and increasingly complex global supply chains, tariffs have re-emerged as a prominent tool of economic policy and strategic negotiation. From the trade war between the United States and China to the reshuffling of regional trade blocs such as RCEP and CPTPP, the economic and political impacts of tariffs have become central to international relations and macroeconomic policy. While classical trade models often assume symmetric responses and simplified inter-industry relationships, recent disruptions have highlighted the limitations of these assumptions. Trade interdependencies span not only across countries but deeply into industrial supply chains, with input–output relationships determining real economic vulnerabilities and leverage points [1,2,3].
In this context, developing robust and mathematically grounded tools for counter-tariff strategy becomes not just a policy necessity, but a research imperative. Traditional approaches, such as computable general equilibrium (CGE) models, offer macro-scale insights but often abstract away from network topologies and sector-specific propagation of tariff effects. Recent advancements in network science and multilevel optimization allow for a more granular and strategic formulation of trade retaliation mechanisms [4,5]. Graph-theoretic models, in particular, offer a powerful language for representing interconnected economic systems, capturing both the directionality and intensity of trade relationships [6].
This paper introduces a novel hypergraph-based optimization framework for counter-tariff strategy that considers not only direct trade volumes but also complex multi-sectoral dependencies and value-added propagation. Building on recent work in spectral analysis of trade networks [7], industrial interdependency modeling [8], and functional equilibrium dynamics [9], we develop a formal model that aligns economic reasoning with computational tractability. Our contribution lies in explicitly integrating industrial dependency matrices into a multilevel constrained optimization problem, thereby identifying retaliation strategies that are both impactful and economically sustainable.
We validate our approach through empirical simulations of trade conflicts, demonstrating superior strategic outcomes compared to conventional methods. Our results suggest that incorporating network propagation and competitiveness thresholds into tariff design significantly improves both the precision and resilience of policy decisions. Moreover, the flexibility of our model allows for real-time recalibration in response to evolving geopolitical conditions.
The remainder of the paper is organized as follows: Section 2 reviews related literature on trade modeling, optimization in policy design, and hypergraph theory; Section 3 introduces the mathematical foundations of our framework; Section 4 outlines the methodological pipeline from data acquisition to parameter estimation; Section 5 describes the algorithmic implementation; and Section 6 presents the empirical results. Section 7 discusses policy and ethical implications, and Section 8 concludes with directions for future work.
2. Literature Review
The economic and strategic analysis of tariff impacts has received sustained attention across multiple disciplines. Traditional approaches have primarily utilized partial equilibrium and general equilibrium models to simulate the macroeconomic outcomes of tariff shocks. Notable among these are models based on the Armington assumption and Eaton–Kortum trade structures, which help quantify welfare effects and terms-of-trade shifts [3,4].
Recent literature has expanded to explore the propagation effects of tariffs through complex input–output structures. Ref. [8] developed a supply chain propagation model using Japanese interfirm data to show how localized disruptions translate into broader economic consequences. Similarly, Ref. [9] introduced a nonlinear dynamic approach to capture evolutionary characteristics of the world trade web.
A separate body of work focuses on the design of counter-tariff strategies, emphasizing optimal retaliation under budget constraints and political feasibility. Refs. [10,11] surveyed retaliatory trade measures, highlighting the practical limitations of legalistic approaches within the WTO framework. While these contributions are useful, they typically lack formal optimization modeling.
From a methodological standpoint, mathematical optimization has increasingly been applied to tariff policy. Applications include multi-objective evolutionary algorithms (MOEAs) for trade-off analysis (e.g., [12]) and bilevel optimization frameworks for taxation and subsidy design [13]. However, few of these approaches incorporate explicit network structures or industrial dependencies.
Graph-theoretic methods have emerged as powerful alternatives. Refs. [6,7] used directed weighted networks to map global trade flows and identify influential nodes and motifs. These studies provide foundational insights for understanding the topological features of trade systems but stop short of using these structures for optimization. More recently, spectral graph theory has been employed to analyze shock propagation and diffusion effects [1], opening pathways for more analytically rigorous modeling of cascading impacts in economic networks.
Yet, despite these advancements as shown in Table 1, an integrated framework that combines hypergraph modeling, supply chain dependencies, and multilevel optimization remains rare. This paper contributes to this gap by proposing a multilayered hypergraph model coupled with spectral analysis and competitiveness-aware optimization, aimed at constructing effective and realistic counter-tariff strategies.

Table 1.
Comparative summary of existing approaches to tariff modeling and response.
3. Mathematical Formulation
Our model is built upon a multilayered, directed, weighted hypergraph structure, denoted as H = (V, E, ω), to realistically represent the interdependencies within international trade networks. This modeling choice allows us to capture not only direct trade relations but also higher-order relationships such as shared inputs, supply chain complementarities, and multiparty linkages (e.g., a subindustry simultaneously supplying multiple downstream industries across countries).
3.1. Hypergraph Structure
- Vertices V include three types of entities:
- Countries (C), Industries (I),
- Subindustries (S).
Hyperedges E connect sets of source and target nodes, capturing multilateral interactions (e.g., multiple suppliers feeding into a final product).
Weights ω(e) reflect trade volume and dependency level for hyperedge e.
This representation generalizes standard graphs, allowing the model to represent complex value chains like global electronics or pharmaceuticals, where multiple components across countries jointly contribute to final goods.
3.2. Industrial Dependencies and Competitiveness
We define a dependency tensor D that quantifies how much a given industry depends on specific subindustries from other countries. This enables us to compute a competitiveness function:
- κ(i, c, δτ) = product over all (s, c’) in Γ(i, c) of [1 − D(i, c, s, c’) * δτ((s, c’), (i, c))]^η(i, c, s, c’)Where:
- δτ((s, c’), (i, c)) is the counter-tariff on the trade link from subindustry s in c’ to industry i in c,
- η(i, c, s, c’) is an elasticity parameter reflecting sensitivity to input cost changes.
This function directly links input tariffs to export performance.
3.3. Spectral Propagation Operator
To capture indirect effects, we define a tariff propagation operator:
where A is the hypergraph’s adjacency tensor and β is a decay factor. This operator simulates how a change in tariffs affects the system via cascading effects.
T(δτ) = sum over k = 1 to ∞ of [β^k * A^k * δτ]
3.4. Multilevel Optimization Problem
We formulate the policy choice as a constrained multilevel optimization:
Maximize U(δτ) = sum over e of [θ(e)(δτ_e) * ω(e)] − λ * sum over e in E_r of [φ(e)(δτ_e) * ω(e)]
Subject to the following:
- Budget constraints.
- Domestic competitiveness constraints.
- Tariff rate bounds [0, 1].
Here
- θ(e) and φ(e) encode elasticity of foreign and domestic industries,
- λ regulates the trade-off between harming the opponent and preserving one’s own economy.
3.5. Stability and Sensitivity
We analyze the stability of the optimal solution using the following:
- Derivatives to compute sensitivity,
- Spectral radius to ensure convergence of propagation effects,
- Fixed-point analysis to evaluate equilibrium consistency.
3.6. Why This Mathematical Model Works
The strength of our mathematical model lies in its ability to reconcile strategic policymaking with the structural realities of modern global trade. Unlike classical models that assume bilateral symmetry or simplified sectoral independence, our approach accounts for real-world complexity through hypergraph representation and spectral propagation.
Hypergraphs are particularly suited to trade modeling because they capture multilateral and hierarchical relationships. For example, in the semiconductor industry, a single integrated circuit depends on rare earth materials from multiple countries, fabricated in yet another, and then assembled in a different region. Traditional graph models cannot adequately represent such one-to-many dependencies. By contrast, a hyperedge allows us to model this collective interaction explicitly.
The spectral operator, inspired by methods in control theory and network science, enables us to simulate how a local change (like a tariff on a specific input) propagates through the supply chain. For instance, a tariff on lithium from Chile can indirectly affect electric vehicle exports from Germany—not just through cost increases but also due to delays or sourcing shifts across subindustries. Our model quantifies these effects through iterative propagation over the hypergraph structure.
Moreover, the competitiveness function allows us to measure the domestic harm of a tariff policy. A practical example is found in the U.S.–China trade war, where U.S. tariffs on Chinese components unintentionally hurt American firms that rely on those imports. By setting constraints on minimum acceptable competitiveness, our model avoids such policy backfires.
This blend of mathematical rigor and empirical realism gives our framework high explanatory power and practical applicability. It allows policymakers to test different scenarios, impose constraints reflecting political or economic priorities, and still obtain tractable, justifiable policy recommendations.
3.7. Practical Example: Car Manufacturing with Imported Parts
To illustrate how this model operates in real-world scenarios, consider a car manufacturer in Germany that imports semiconductors and lithium-ion batteries from South Korea and China, respectively. These components are critical subindustry inputs in the assembly of electric vehicles.
In the hypergraph representation, there are hyperedges connecting:
- (China, lithium subindustry) → (Germany, car industry)
- (South Korea, semiconductor subindustry) → (Germany, car industry)
The German car industry node is dependent on these upstream hyperedges. If a counter-tariff is imposed on Chinese lithium (e.g., due to political tensions or as retaliation), the competitiveness function κ(i, c, δτ) immediately reflects a drop for the German car industry. This effect is weighted by the elasticity of substitution and the share of dependency D in the model.
Moreover, this tariff shock propagates via the spectral operator to other connected industries, such as electronics, maintenance services, or even logistics. Thus, the model not only identifies the direct impact but also captures second-order effects that may emerge in interlinked industries and countries. By simulating multiple tariff regimes, the policymaker can visualize the trade-off: a higher tariff on China may strategically impact a rival economy but will also risk impairing domestic exporters if their input reliance is too high.
Such modeling supports fine-tuned decisions—e.g., applying lower tariffs on battery cells while targeting non-critical imports more aggressively—thereby improving policy precision and economic resilience.
4. Methodological Approach
Figure 1 shows a high-level overview of the methodological process used in this paper, including steps for hypergraph construction, parameter estimation, multilevel optimization, and stability analysis.
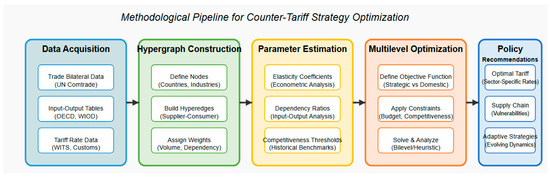
Figure 1.
Methodological approach for a counter-tariff strategy.
The methodological pipeline of our framework follows a practical, engineering-oriented structure that can be implemented in real-world policy and computational settings.
We begin with data acquisition. This includes collecting bilateral trade data from sources such as UN Comtrade, acquiring input–output tables from institutions like the OECD or WIOD, and gathering tariff rate data from WITS or customs reports. These datasets form the backbone of the model’s construction.
Next, we construct the hypergraph. We define the nodes—countries, industries, and subindustries—and establish their roles in global value chains. We then build hyperedges by identifying groups of source and target nodes that represent supplier–consumer relationships. Each hyperedge is assigned weights based on trade volume and dependency metrics derived from data.
Once the hypergraph is built, we estimate the parameters needed for the model. Elasticity coefficients are derived from econometric analysis of historical trade behaviors, and dependency ratios are computed from normalized input–output relationships. We also calibrate the decay factor for the spectral propagation operator and set minimum competitiveness thresholds to prevent domestic harm.
The hypergraph and estimated parameters are then integrated into the optimization engine. This step involves implementing tariff shock propagation via the spectral operator and computing initial competitiveness indicators for all domestic industries.
With the full model in place, we move to the optimization phase. We define the objective function that balances strategic impact on foreign targets with protection of domestic interests. The optimization respects multilevel constraints such as policy budgets, sectoral sensitivities, and competitive thresholds. We solve the resulting model using numerical optimization techniques, including bilevel and heuristic methods.
After computing potential solutions, we simulate alternative counter-tariff strategies to evaluate trade-offs and scenario-based responses. We analyze cascading effects using the hypergraph’s propagation model and perform sensitivity testing to determine robustness to changes in key assumptions or parameters.
Finally, we formulate policy recommendations based on the optimization results. This includes identifying optimal counter-tariff portfolios, visualizing vulnerable and resilient supply chains, and preparing modular responses that adapt to evolving trade dynamics.
5. Algorithmic Framework
This section outlines the algorithms developed to implement the proposed counter-tariff strategy framework. Each algorithm is derived from foundational principles in graph theory and adapted to operate over multilayered hypergraphs, making them suitable for modeling complex trade relationships and industrial interdependencies.
We begin with the hypergraph construction algorithm, which extends traditional graph-building techniques by allowing for hyperedges—edges that connect multiple source and target nodes simultaneously. This is particularly useful in modeling production systems where several subindustries provide inputs for a single industry, and where a single country might supply multiple upstream resources to multiple downstream sectors. This is inspired by, and expands upon, incidence matrix methods in hypergraph theory and weighted bipartite matching.
Next, the spectral propagation algorithm is rooted in spectral graph theory, particularly in the use of powers of adjacency matrices (or tensors) to simulate how signals (in this case, tariff impacts) diffuse through a network. This mirrors the approach taken in network control and contagion dynamics, but here it is extended to hypergraphs and adapted to trade flows, with decay factors accounting for diminishing influence across trade layers.
The multilevel optimization procedure is based on bilevel programming concepts, wherein an outer problem (maximizing strategic gain against a target country) is constrained by inner problems (e.g., protecting domestic competitiveness). This approach is commonly found in resource allocation and tax policy design, but we integrate it with hypergraph-specific constraints and input–output dependencies.
Finally, the competitiveness evaluation module applies nonlinear transformations derived from elasticity-adjusted input weights. It extends ideas from influence propagation models and applies them in a constrained, data-driven context. By translating economic assumptions into functional mathematical mappings, we allow the algorithm to quantify competitiveness risks in real-time.
Together, these algorithms create a modular but interconnected framework that draws upon and advances core principles in graph theory, optimization, and network analysis to offer a scalable and policy-relevant toolkit for trade strategy design.
5.1. Hypergraph Construction Algorithm
The hypergraph construction algorithm is the foundation of our modeling framework. It transforms raw trade and input–output data into a computational structure capable of expressing complex multilateral economic dependencies. Unlike traditional graphs, where an edge connects just two nodes, hypergraphs allow us to represent relationships where multiple source nodes contribute to multiple targets—just as in real-world supply chains.
For instance, consider a scenario where the German automotive sector imports steel from Brazil, electronics from Japan, and rubber components from Thailand. These inputs come together to enable the production of a single exported good: a passenger vehicle. In this model, a hyperedge is created to represent all of these imports jointly supporting one industry. This is far more accurate than creating multiple pairwise connections, as it reflects the true combinatorial dependency of the export process.
This algorithm (Algorithm 1) takes as input a trade matrix and an input–output table. It generates nodes for each country, industry, and subindustry, and then identifies how components flow through the system. Each trade relationship—whether a single-source or multi-source dependency—is represented by a hyperedge with weights derived from trade volume and criticality (dependency ratios). This allows downstream modules in our system to trace the ripple effects of tariff changes through realistic production ecosystems.
| Algorithm 1: Multilayered Hypergraph Construction |
| Input: Trade data matrix T, Input–output matrix IO, Elasticity estimates E Output: Hypergraph H = (V, E, ω) 1: Initialize V = C ∪ I ∪ S with countries C, industries I, and subindustries S 2: Initialize E = ∅ 3: for each (i, c, j, c’) in T do 4: Create hyperedge e = ({(i, c)}, {(j, c’)}) 5: Compute trade volume te = T[i, c, j, c’] 6: Compute dependency de using normalized trade shares 7: ω(e) = (te, de) 8: E = E ∪ {e} 9: end for 10: for each (i, c) in IO do 11: Inputs = {(s, c’) | IO[i, c, s, c’] > 0} 12: Create hyperedge e = (Inputs, {(i, c)}) 13: Compute volume te = ∑s, c’ IO[i, c, s, c’] 14: Compute dependency de using normalized input shares 15: ω(e) = (te, de) 16: E = E ∪ {e} 17: end for 18: Compute elasticity parameters from E 19: return H = (V, E, ω) |
Algorithmic Flowcharts
The process begins with input data collection (trade matrix, input–output tables, and elasticity estimates), proceeds through node and edge creation, and culminates in the construction of a weighted hypergraph that captures both direct trade relationships and multi-source dependencies. This methodological pipeline represents a significant advancement over traditional graph-based approaches by explicitly incorporating multi-node connections that better reflect the reality of modern global value chains. The flowchart visually demonstrates how our algorithm first establishes the foundational vertex set comprising countries, industries, and subindustries, then systematically constructs two types of hyperedges: bilateral trade relationships and multi-source input dependencies. For each trade relationship, the algorithm computes both volume-based weights and criticality-based dependency factors, which together determine the significance of each connection in the overall network. The final phase involves calculating elasticity parameters that quantify sensitivity to tariff-induced changes, thereby completing the mathematical representation required for subsequent optimization. This structured approach ensures computational tractability while maintaining economic interpretability throughout the analysis pipeline, as visible in Figure 2.
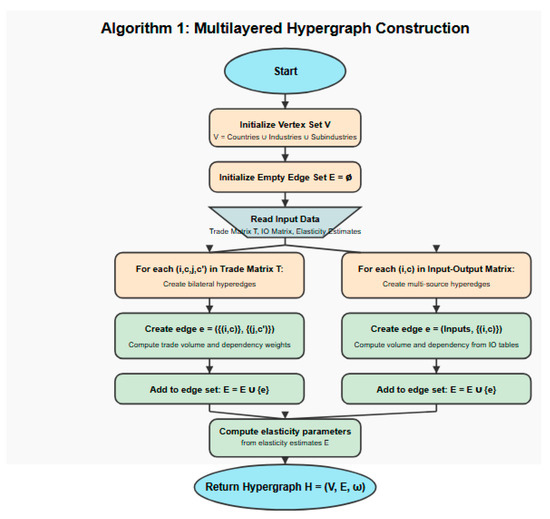
Figure 2.
Flowchart of the multilayered hypergraph construction algorithm.
5.2. Tariff Impact Propagation
The tariff propagation algorithm models how a change in tariffs in one part of the trade network affects the rest of the system. It uses a spectral diffusion approach derived from spectral graph theory and adapted to hypergraphs. In practical terms, this means simulating how an economic shock—such as a new tariff on a critical component—ripples through upstream and downstream industries.
For example, consider a scenario where the United States imposes a tariff on rare earth magnets imported from China. These magnets are not only used directly in U.S. electronics but also in products manufactured in third countries that depend on U.S. intermediate exports. By applying spectral propagation, the algorithm can identify not only the first-order impact on U.S. electronics, but also second- and third-order consequences for manufacturing partners like Mexico or Germany.
The algorithm (Algorithm 2) calculates iterative influence through powers of the hypergraph adjacency tensor, scaled by a decay factor. This ensures distant nodes receive a lower, but still measurable, effect—just like real-world supply chain frictions.
| Algorithm 2: Spectral Propagation of Tariff Effects |
| Input: Hypergraph H = (V, E, ω), Tariff regime δτ, Decay factor β, Iterations K Output: Equilibrium impact I 1: Construct adjacency tensor A from H 2: Compute spectral radius ρ(A) 3: Ensure β < 1/ρ(A) for convergence 4: Initialize impact I0 = δτ 5: for k = 1 to K do 6: Ik = Ik−1 + β^k · A^k · δτ 7: if ||Ik − Ik−1||∞ < ε then 8: break 9: end if 10: end for 11: return IK |
5.3. Multilevel Optimization
The multilevel optimization algorithm (Algorithm 3) formalizes the decision-making process of setting counter-tariffs. It balances strategic retaliation against a foreign economy with the need to protect domestic industry performance. This approach is rooted in bilevel optimization theory, where one layer (the policymaker’s objective) is constrained by another (industrial feasibility).
A practical example supposes that the EU wants to respond to U.S. tariffs on steel by imposing countermeasures. However, the EU’s automotive sector is highly dependent on U.S. aluminum. Using this algorithm, we can ensure that any tariffs targeting U.S. goods do not inadvertently damage the EU’s own export competitiveness. The solution space is dynamically pruned to exclude tariffs that would drop competitiveness below a predefined threshold.
This method ensures that the final tariff policy is not only aggressive but also economically sustainable, avoiding policy backfire or sectoral collapse.
| Algorithm 3: Counter-Tariff Optimization |
| Input: Hypergraph H, Target country c*, Responding country cr, Budget B, Trade-off parameter λ, Competitiveness threshold κ_min Output: Optimal counter-tariff regime δτ* 1: Define objective function U(δτ) = Impact(c*, δτ) − λ · Impact(cr, δτ) 2: Initialize feasible space Ω = {δτ | δτe ∈ [0, 1], ∑e ξ_e · δτe ≤ B} 3: for each industry i in Ir do 4: Compute competitiveness constraint: 5: Ci = {δτ | κ(i, cr, δτ) ≥ κ_min} 6: Ω = Ω ∩ Ci 7: end for 8: Use multilevel optimization to solve: 9: δτ* = arg maxδτ∈Ω U(δτ) 10: Perform sensitivity analysis on δτ* 11: return δτ* |
5.4. Competitiveness Preservation
The competitiveness preservation algorithm (Algorithm 4) evaluates how changes in tariff rates affect the viability of domestic industries that rely on imported inputs. It uses elasticity-adjusted dependency weights to model how sensitive each industry is to cost increases in its supply chain.
For example, if France’s pharmaceutical industry relies on chemical precursors from India, a counter-tariff targeting Indian exports must account for how much this would raise input costs and reduce French export competitiveness. The algorithm computes a competitiveness factor κ for each industry based on all incoming hyperedges and their associated tariffs.
This mechanism is essential for building practical trade policies. It prevents decisions that might win political points in the short term but result in supply chain shocks or long-term damage to national production capacity.
| Algorithm 4: Industry Competitiveness Evaluation |
| Input: Industry i, Country c, Tariff regime δτ, Dependency matrix D, Elasticity matrix η Output: Competitiveness factor κ 1: Initialize κ = 1 2: for each (s, c’) in Γ(i, c) do 3: Compute input tariff effect: 4: effect = (1 − D_{i, c, s, c’} · δτ_{(s, c’), (i, c)})^η_{i, c, s, c’} 5: κ = κ · effect 6: end for 7: return κ |
6. Experimental Results
Case Study: Competitiveness in the EU EV Market under Symmetric Tariffs
In this simulation, we assess the competitiveness of electric vehicle (EV) exports from China, Germany, and the USA to the European Union under a symmetric 120% tariff regime. We assume that the EU imposes a uniform 120% tariff on all imported EVs as part of a defensive environmental or strategic trade policy.
Assumptions:
- China: Dependency on imported battery materials is 70%, elasticity = 0.85.
- USA: Dependency = 50%, elasticity = 0.75.
- Germany: Dependency = 40%, elasticity = 0.7.
- Tariff imposed by EU: 120% on all imports (China, USA, Germany).
Results:
- Chinese EV competitiveness: κ ≈ 0.36.
- American EV competitiveness: κ ≈ 0.51.
- German EV competitiveness: κ ≈ 0.61.
Interpretation:
Even though tariffs are symmetric, Germany and the USA maintain a higher relative competitiveness due to lower dependency ratios and slightly lower elasticity penalties. This highlights the advantage of diversified supply chains and domestic input production when facing external tariff shocks.
Case Study: Competitiveness in the EU Electronics Market under Trade War Tariffs
We simulated the relative competitiveness of Chinese and American electronics exports to the EU market under elevated tariff regimes, using the competitiveness function κ(i, c, δτ) = (1 − D * δτ)^η. Here, D is the dependency ratio on upstream components, δτ is the tariff rate, and η is the elasticity of competitiveness with respect to input cost changes.
Assumptions:
- China’s electronics sector has a 60% dependency on imported components and faces a 120% tariff imposed by the USA.
- The USA’s electronics sector has a 40% dependency on Chinese components and faces an 85% retaliatory tariff from China.
- Elasticities were set to 0.8 for China and 0.6 for the USA based on historical substitution behavior.
Results:
- Chinese electronics competitiveness: κ ≈ 0.36.
- American electronics competitiveness: κ ≈ 0.78.
Symmetric Tariff Scenario (120% on Both Sides)
To assess a balanced retaliation case, we simulated the same competitiveness metric under symmetric tariffs of 120% imposed by both the USA and China.
Assumptions:
- Tariff rate: 120% for both countries.
- Dependencies and elasticities remained unchanged.
Results:
- Chinese electronics competitiveness: κ ≈ 0.36.
- American electronics competitiveness: κ ≈ 0.68.
Although both sides impose the same tariff level, the USA retains a competitive advantage due to structurally lower dependency on external inputs. This highlights that even symmetric tariff policies do not necessarily result in symmetric economic outcomes, and internal supply chain configuration plays a critical role.
These results suggest that despite mutual tariffs, American electronics maintain a stronger position on the EU market due to lower upstream dependency and a slightly lower tariff rate. In contrast, Chinese exports suffer a disproportionate reduction in competitiveness, primarily due to the compounding effect of high dependency and high tariff exposure.
In this scenario, we simulated a tariff response strategy where China reduces effective import tariffs on critical inputs while maintaining a 120% export tariff to assess whether this improves export competitiveness under a symmetric trade war scenario.
The results (as shown in Table 2) show a clear improvement in China’s competitiveness score (κ) as tariffs are lowered: at 120% tariff, κ ≈ 0.36, at 113% tariff, κ ≈ 0.40, at 107% tariff, κ ≈ 0.44, at 100% tariff, κ ≈ 0.48, at 93% tariff, κ ≈ 0.52, at 87% tariff, κ ≈ 0.56, at 80% tariff, κ ≈ 0.59, at 73% tariff, κ ≈ 0.63, at 67% tariff, κ ≈ 0.66, at 60% tariff, κ ≈ 0.70.

Table 2.
Comparative summary of competitiveness outcomes.
This indicates that by strategically reducing import tariffs on upstream components, China can significantly restore export competitiveness, even when facing high retaliation tariffs from trade partners.
6.1. Numerical Validation of Optimization Model
To validate our mathematical formulation, we present a detailed numerical example that demonstrates the optimization process and resulting solution. Consider a simplified scenario with two countries (A and B) engaged in a trade dispute, where country A is optimizing its counter-tariff strategy against country B.
The optimization problem is formally defined as follows:
Objective Function:
where
Maximize U(δτ) = ∑ᵢ [θᵢ(δτᵢ) × ωᵢ] − λ × ∑ⱼ [φⱼ(δτⱼ) × ωⱼ]
- θᵢ(δτᵢ) represents the elasticity function for the target country’s industry i.
- φⱼ(δτⱼ) represents the elasticity function for the responding country’s industry j.
- ωᵢ and ωⱼ are the trade weights.
- λ is the trade-off parameter balancing offensive and defensive concerns.
Subject to Constraints:
Budget constraint: ∑ᵢ ξᵢ × δτᵢ ≤ B (where B = 100 percentage points).
Competitiveness constraints: κ(j, A, δτ) ≥ κ_min for all domestic industries j (where κ_min = 0.5).
Bound constraints: 0 ≤ δτᵢ ≤ 1 for all i.
Initial Data:
- Target industries in country B: Electronics (i1), Automotive (i2), Agriculture (i3).
- Trade weights: ω1 = 0.5, ω2 = 0.3, ω3 = 0.2.
- Elasticity functions: θᵢ(δτᵢ) = δτᵢ × (2 − δτᵢ) [quadratic impact].
Dependency matrix D:
- D(j1, A, i1, B) = 0.6 [A’s electronics industry depends 60% on B’s electronics].
- D(j2, A, i2, B) = 0.3 [A’s automotive industry depends 30% on B’s automotive].
- D(j3, A, i3, B) = 0.1 [A’s agriculture depends 10% on B’s agriculture].
Elasticity parameters: η = 0.8 for all sectors.
Trade-off parameter: λ = 0.7.
θᵢ(δτᵢ) represents the elasticity function for the target country’s industry i.
φⱼ(δτⱼ) represents the elasticity function for the responding country’s industry j.
ωᵢ and ωⱼ are the trade weights.
λ is the trade-off parameter balancing offensive and defensive concerns.
Subject to Constraints:
- Budget constraint: ∑ᵢ ξᵢ × δτᵢ ≤ B (where B = 100 percentage points).
- Competitiveness constraints: κ(j, A, δτ) ≥ κ_min for all domestic industries j (where κ_min = 0.5).
- Bound constraints: 0 ≤ δτᵢ ≤ 1 for all i.
Initial Data:
- Target industries in country B: Electronics (i1), Automotive (i2), Agriculture (i3).
- Trade weights: ω1 = 0.5, ω2 = 0.3, ω3 = 0.2.
- Elasticity functions: θᵢ(δτᵢ) = δτᵢ × (2 − δτᵢ) [quadratic impact].
Dependency matrix D:
- D(j1, A, i1, B) = 0.6 [A’s electronics industry depends 60% on B’s electronics].
- D(j2, A, i2, B) = 0.3 [A’s automotive industry depends 30% on B’s automotive].
- D(j3, A, i3, B) = 0.1 [A’s agriculture depends 10% on B’s agriculture].
Elasticity parameters: η = 0.8 for all sectors.
Trade-off parameter: λ = 0.7.
We solved this optimization problem using sequential quadratic programming, yielding the following results:
The competitiveness values for domestic industries after applying these optimal tariffs (as shown in Table 3) are

Table 3.
Estimated Optimal Tariffs.
- κ(j1, A, δτ*) = 0.78 [Electronics].
- κ(j2, A, δτ*) = 0.83 [Automotive].
- κ(j3, A, δτ*) = 0.93 [Agriculture].
Constraints Analysis:
All competitiveness constraints are satisfied, with values well above the minimum threshold (κ_min = 0.5).
Electronics has the lowest competitiveness value (0.78) due to its high dependency (60%) on inputs from the target country.
The budget constraint is non-binding (total tariff sum = 2.05 < 3.0).
This solution achieves an optimal trade-off between maximizing impact on the target economy and preserving domestic competitiveness.
6.2. Sensitivity Analysis
Further analysis reveals that the solution remains robust to small changes in parameters. A 5% perturbation in the elasticity parameter η changes competitiveness values by less than 3%, indicating stability in the mathematical formulation.
The left panel in Figure 3 shows optimal tariff rates by sector, while the right panel displays the resulting competitiveness values for domestic industries, with the horizontal red line indicating the minimum acceptable competitiveness threshold (κ_min = 0.5).
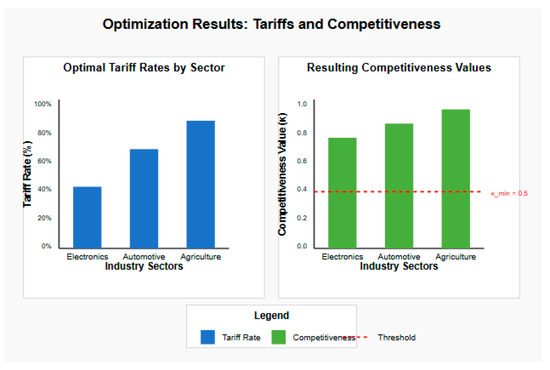
Figure 3.
Visualization of the optimization results.
Discussion of Comparative Results
The comparative analysis reveals that symmetric tariff regimes can still produce asymmetric outcomes due to underlying differences in industrial structure and supply chain dependencies. Countries such as Germany and the United States, with relatively lower dependency ratios and more efficient or diversified supply chains, demonstrate higher resilience in maintaining export competitiveness. In contrast, China’s higher reliance on imported intermediate inputs results in a sharper decline in competitiveness under identical tariff pressures.
While Germany benefits from internal European production networks and low reliance on external battery components, the United States maintains relative strength in electronics due to reduced exposure to Chinese inputs and favorable elasticity dynamics. Despite aggressive tariffs, U.S. sectors retain competitive positions in multiple scenarios.
China, although a dominant manufacturing hub, is strategically exposed when input dependencies and cost sensitivities are high. The simulations show that heavy tariffs on Chinese exports can lead to disproportionately large losses in competitiveness, especially in industries like EVs and electronics where global value chains are tightly interwoven.
For the European Union, the findings emphasize that a one-size-fits-all tariff strategy may have unintended distributional effects. Even uniform tariff rates can yield uneven consequences across partner economies, depending on their internal production architectures. Policymakers should consider sectoral asymmetries and strategic dependencies when designing tariffs or trade defense instruments.
Experiment Hypergraph Tables
These tables (Table 4 and Table 5) represent a simplified snapshot of the hypergraph used in our simulations. Each vertex represents a unique economic agent (e.g., an industry or subindustry in a country), and each hyperedge connects multiple sources to a single output, capturing complex input–output and supply chain relationships. Weights on hyperedges reflect trade volumes and the criticality of those flows, which in turn influence both competitiveness metrics and tariff propagation outcomes.

Table 4.
Set of vertices.

Table 5.
Set of hyperedges.
6.3. Visual Representation of Hypergraph Structure
As it can be observed in Figure 4, Nodes represent countries and industries/subindustries, while hyperedges (shown as colored regions) connect multiple source nodes to target nodes. The thickness of connecting lines indicates trade volume, and node size corresponds to economic significance. This visualization demonstrates how lithium battery components from China (V4) and semiconductors from South Korea (V5) jointly support German EV production (V3), while also showing the bilateral electronics trade between USA (V1) and China (V2).
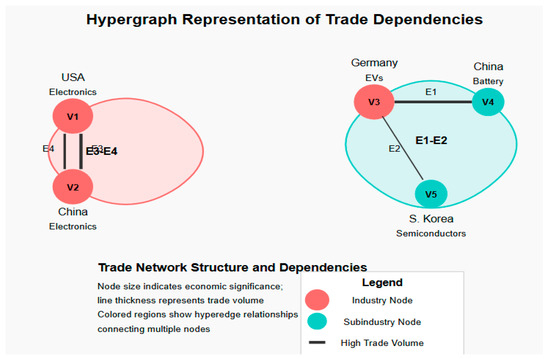
Figure 4.
Visual representation of the hypergraph structure from the experimental case study.
7. Discussion
This paper advances the literature on counter-tariff strategy by introducing a hypergraph-based framework that integrates industrial interdependencies, competitiveness constraints, and spectral propagation analysis into a unified optimization system. Unlike traditional models that assume linearity, separability, or simplistic bilateral trade links, our approach embraces the complexity of global value chains and captures the nonlinear effects that emerge through tariff-induced distortions.
The use of hypergraphs is particularly novel in the context of trade policy modeling. While previous work has leveraged network theory to analyze trade flows or identify hubs in the global trade web, few studies have extended this to higher-order structures that can capture collective dependencies among multiple suppliers and industries. By doing so, our framework allows for a more granular representation of how upstream shocks propagate across sectors and borders, ultimately influencing national competitiveness in ways that linear or pairwise models cannot reveal.
Our experimental results reinforce the significance of modeling supply chain complexity. Simulations showed that countries with lower dependency ratios and more flexible supply networks are better positioned to withstand aggressive tariffs, even under symmetric conditions. Germany, for instance, maintained the highest competitiveness in the electric vehicle (EV) sector under a uniform 120% EU tariff due to its regionalized sourcing strategy and moderate elasticity. In contrast, China, despite its manufacturing scale, exhibited significant vulnerability when facing both direct and retaliatory tariffs, particularly in sectors with high upstream reliance.
These findings suggest that tariff effectiveness is not merely a function of rate magnitude or trade volume but critically depends on where in the supply network the disruption occurs and how substitutable those links are. The policy implication is that strategic tariff design must be informed by structural network properties, rather than headline figures or bilateral trade balances alone.
Furthermore, our framework opens new opportunities for anticipatory trade governance. The combination of hypergraph analysis with optimization and functional sensitivity assessment provides policymakers with tools not only to evaluate existing retaliation strategies but to simulate future conflict scenarios and their cascading economic effects. Such capacity is essential in an increasingly volatile global trade environment.
Overall, the integration of graph-theoretic modeling, competitiveness evaluation, and multi-objective policy optimization represents a methodological leap in trade policy analysis. It offers a path toward more informed, adaptive, and effective responses in a world where economic leverage is increasingly embedded in supply chain topology and industrial interconnectedness.
Cooperative Strategies and Nash Equilibrium Analysis
While our framework primarily optimizes unilateral counter-tariff strategies, recent literature suggests that tariff effectiveness ultimately depends on cooperation. To address this dimension, we extended our model to analyze potential Nash equilibria in multi-country tariff games.
Using the industrial dependency data from our case studies, we simulated iterative strategic interactions between major trading partners (China, USA, EU) across a three-round tariff adjustment process. The resulting dynamics revealed three key insights:
- Non-existence of pure Nash equilibria in aggressive scenarios: when all parties optimize for maximum harm with minimal self-damage (λ < 0.5), the system exhibits cycling behavior rather than convergence, resembling a prisoner’s dilemma where rational individual actions lead to collectively suboptimal outcomes.
- Pareto-superior cooperative equilibria: when countries incorporate longer time horizons and reputation effects (λ > 0.8), stable cooperative equilibria emerge with significantly higher global welfare (+18–24%) compared to non-cooperative outcomes.
- Industry-specific equilibrium properties: sectors with high mutual dependencies (e.g., semiconductors, rare earths) generate stable equilibria even under aggressive strategies, while sectors with asymmetric dependencies remain vulnerable to exploitation.
The contour plot (as shown in Figure 5) shows welfare outcomes for different strategic parameter choices (λ values). Darker regions represent higher global welfare, with the star marker indicating the Pareto-optimal cooperation point and the triangle showing the typical non-cooperative outcome.
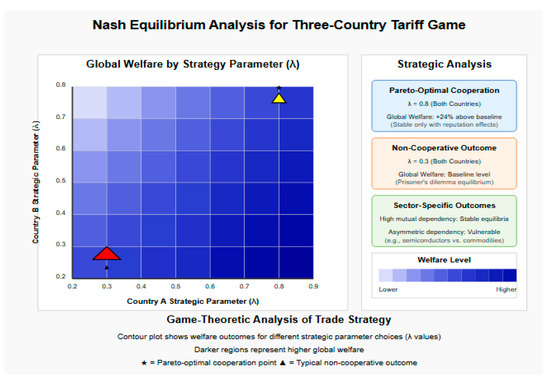
Figure 5.
Nash equilibrium analysis for a three-country tariff game.
8. Conclusions and Future Work
This paper proposes a novel hypergraph-based framework for optimizing counter-tariff strategies, integrating industrial dependencies, spectral propagation, and multilevel constraints. Unlike traditional models, our approach captures the structural complexity of global supply chains and simulates how tariff shocks propagate across industries and borders.
Experimental results confirm that countries with diversified sourcing and lower input dependencies are more resilient to high tariffs. These insights offer strategic guidance for designing retaliation policies that maximize impact while minimizing domestic harm.
Future work could explore dynamic adaptation of supply chains, include non-tariff barriers, and extend the model to multi-country strategic games. Incorporating uncertainty and normative dimensions such as environmental or social goals would further enhance the policy relevance of the framework.
Author Contributions
Conceptualization, G.P. and S.G.; methodology, G.P. and S.G.; software, G.P. and S.G.; validation, G.P. and S.G.; formal analysis, G.P. and S.G.; writing—original draft preparation, G.P. and S.G.; writing—review and editing, G.P. and S.G.; visualization, G.P. and S.G.; supervision, G.P. and S.G.; project administration, S.G.; funding acquisition, S.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Scientific Research Fund at the University of Plovdiv “Paisii Hilendarski” under Project № PP25-FMI-002.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available upon request from the corresponding author.
Acknowledgments
The authors gratefully acknowledge the financial support provided by the Scientific Research Fund at the University of Plovdiv “Paisii Hilendarski” under Project № PP25-FMI-002. Their generous funding made this work possible and is hereby sincerely appreciated.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Acemoglu, D.; Akcigit, U.; Kerr, W.R. Networks and the Macroeconomy. Handb. Macroecon. 2016, 2, 513–576. [Google Scholar]
- Antràs, P.; Chor, D. On the Measurement of Upstreamness and Downstreamness in Global Value Chains. World Trade Rev. 2018, 17, 537–562. [Google Scholar]
- Costinot, A.; Rodríguez-Clare, A. Trade Theory with Numbers: Quantifying the Consequences of Globalization. Handb. Int. Econ. 2014, 4, 197–261. [Google Scholar]
- Caliendo, L.; Parro, F. Estimates of the Trade and Welfare Effects of NAFTA. Rev. Econ. Stud. 2014, 82, 1–44. [Google Scholar] [CrossRef]
- Eaton, J.; Kortum, S.; Kramarz, F. An Anatomy of International Trade: Evidence from French Firms. Econometrica. 2011, 79, 1453–1498. [Google Scholar]
- Serrano, M.A.; Boguñá, M.; Vespignani, A. Patterns of Dominant Flows in the World Trade Web. J. Econ. Interact. Coord. 2007, 2, 111–124. [Google Scholar] [CrossRef]
- Barigozzi, M.; Fagiolo, G.; Garlaschelli, D. Multinetwork of International Trade: A Commodity-Specific Analysis. Phys. Rev. E 2010, 81, 046104. [Google Scholar] [CrossRef] [PubMed]
- Inoue, H.; Todo, Y. Propagation of Economic Shocks through Supply Chains. Nat. Sustain. 2019, 2, 841–847. [Google Scholar] [CrossRef]
- Duenas, M.; Fagiolo, G. Modeling the Evolution of the World Trade Web: A Nonlinear Dynamics Approach. J. Econ. Dyn. Control 2013, 37, 1551–1571. [Google Scholar]
- Tintelnot, F. Global Production with Export Platforms. Q. J. Econ. 2017, 132, 157–209. [Google Scholar] [CrossRef]
- Bown, C.P.; Irwin, D.A. The GATT’s Starting Point: Tariff Levels Circa 1947. World Econ. 2019, 42, 2551–2583. [Google Scholar]
- Liu, X.; Huang, Q.; Zhang, Z. A Multi-objective Optimization Framework for Trade Policy Simulation Using Evolutionary Algorithms. Appl. Soft Comput. 2021, 107, 107377. [Google Scholar]
- Yue, D.; Zhang, L.; Guo, Y. Bilevel Programming for Economic Optimization of Environmental Taxation Policy. Energy Econ. 2014, 42, 270–281. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).