Generalized Net Model for Analysis of Behavior and Efficiency of Intelligent Virtual Agents in Risky Environment ^†

Abstract

In this article, two generalized net models (GNMs) are proposed to study the behavior and effectiveness of intelligent virtual agents (IVA) working in a risky environment under different scenarios and training algorithms. The proposed GNMs allow for the selection of machine learning algorithms such as intensity of characteristics Q-learning (InCh-Q), as well as the modification of multi-plan reinforcement learning (RL), proximal policy optimization (PPO), soft actor–critic (SAC), the generative adversarial imitation learning (GAIL) algorithm, and behavioral cloning (CB). The choice of action, the change in priorities, and the achievement of goals by the IVA are studied under different scenarios, such as fire extinguishing, rescue operations, evacuation, patrolling, and training. Transitions in the GNMs represent the scenarios and learning algorithms. The tokens that pass through the GNMs can be the GNMs of the IVA architecture or the IVA memory model, which are enriched with knowledge and experience during the experiments, as the scenarios develop. The proposed GNMs are formally correct and, at the same time, understandable, practically applicable, and convenient for interpretation. Achieving GNMs that meet these requirements is a complex problem. Therefore, issues related to the design and use of GNMs for the reliable modeling and analysis of the behavior and effectiveness of IVAs operating in a dynamic and risky environment are discussed. Some advantages and challenges in using GNMs compared to other classical models used to study IVA behavior are considered.

1. Introduction

Generalized nets are powerful tools for the simulation of dynamic processes [1]. The theory of generalized nets is being continually developed. For example, intuitionistic fuzzy generalized networks and generalized nets with dynamic priorities in time [2] have been introduced. The possibilities for the merging and splitting of tokens are interesting [3]. An overview of the main new theoretical aspects, as well as interesting results from applications of generalized nets in various scientific and practical areas, are presented in [2]. An overview of the main developments for the software implementation of the theory of generalized nets is presented in [3]. Software components and an integrated environment for the development of generalized nets (GNs IDE) have been implemented, using the Java programming language [4].

GNMs allow the modeling of complex interactions in risky environments (e.g., emergencies, hazardous production, combat simulations, and electrical substations) in which agents have to make decisions in conditions of multiple interdependencies. GNMs can include dynamic parameters, time dependencies, token models that reflect delays, unexpected events, and the uncertainty of risky environments [2]. They allow the investigation of the effectiveness of agent behavior by tracking under which conditions and with which resources agents perform a given task. These models allow for the parallel execution of tasks [5]. They allow the achievement of adaptability [6] by using feedback loops and choosing to pass through other transitions and states when the conditions for action change. Due to its great modeling capabilities, the mathematical apparatus of the generalized net is chosen here to represent and study the behavior of intelligent agents operating in a risky environment.

A generalized net model is proposed to investigate the effectiveness of an intelligent virtual agent in a risky environment for different scenarios using pre-selected machine learning algorithms. The InCh-Q algorithm, published in [7], as well as PPO, SAC, GAIL, and CB, supported by the Unity ML Agent Toolkit, are considered [8,9,10]. GNMs refer to an environment that is static and familiar and in which risky situations dynamically arise in different places at different times. This requires making decisions about actions to choose according to different scenarios. In safe scenarios, the virtual agent patrols, looking for potential opportunities for damage or problems in electrical equipment, or trains users. It visits a sequence of static targets. In risky scenarios, the targets dynamically change because accidents, fires, or injured people can appear in different places at different times. The environment in these cases is dynamic and dangerous.

IVAs are the tokens that move in this virtual world. Each token will be presented by the triple <X, Ф, b>, where

X is a set of initial characteristics of the token;

Ф is a function (let us call it a transforming one) that defines a new characteristic h_i* for each token i with a characteristic hi upon passing the token from the input into the output place of each transition j, while simultaneously obtaining the token k through this transition, with the characteristic h_k,

h_i* = Ф (r_j, h_i, h_k);

(1)

b is the maximum number of characteristics that one token can obtain during its motion in the net.

As a result of these considerations, and according to [1], we obtain the generalized net

E = <<A, π_A, π_L, c, f, θ₁, θ₂>, <K, π_K, θ_K>, <T, t°, t*>, <X, Ф, b>>,

(2)

where the rest of the designations are as follows:

π_A—A → N, where N = {0, 1, 2, …} ∪ {∞}, denoting the priorities of the transitions;

π_L—L → N, where L = pr₁ A ∪ pr₂ and pr_i X denote the i-projection of the n-dimensional set X, n ∈ N, n ≥ i, i ≤ n (L is a set from all places of the GNM);

c—a function giving the capacity of the places, c: L → N;

f—a function that defines the true values of the predicates;

θ₁—a function assigning the subsequent moment from time, in which a given transition can be activated; the value of this function is recalculated in moments when the active condition of the transition is over; θ₁(t) = t’, where t, t’ ∈ [T, T + t*] t ≤ t’;

θ₂—a function giving the duration of the active condition of the transition; θ₂(t) = t’, where t ∈ [T, T + t*] and t’ ≥ 0; the value of the function is calculated when the transition starts functioning.

K is the set of GNM tokens.

π_K is a function assigning the priorities of the tokens, i.e., π_K: K → N.

θ_K is a function assigning moments from time, in which a given token can enter the net, i.e.,

θ_K(α) = t, where α ∈ K, t ∈ [T, T + t*];

T—a moment from time, in which the GN begins to function;

t°—an elementary time step;

t*—the duration of the functioning of the GNM.

2. GNMs for the Analysis of the Effectiveness of IVAs in a Risky Environment

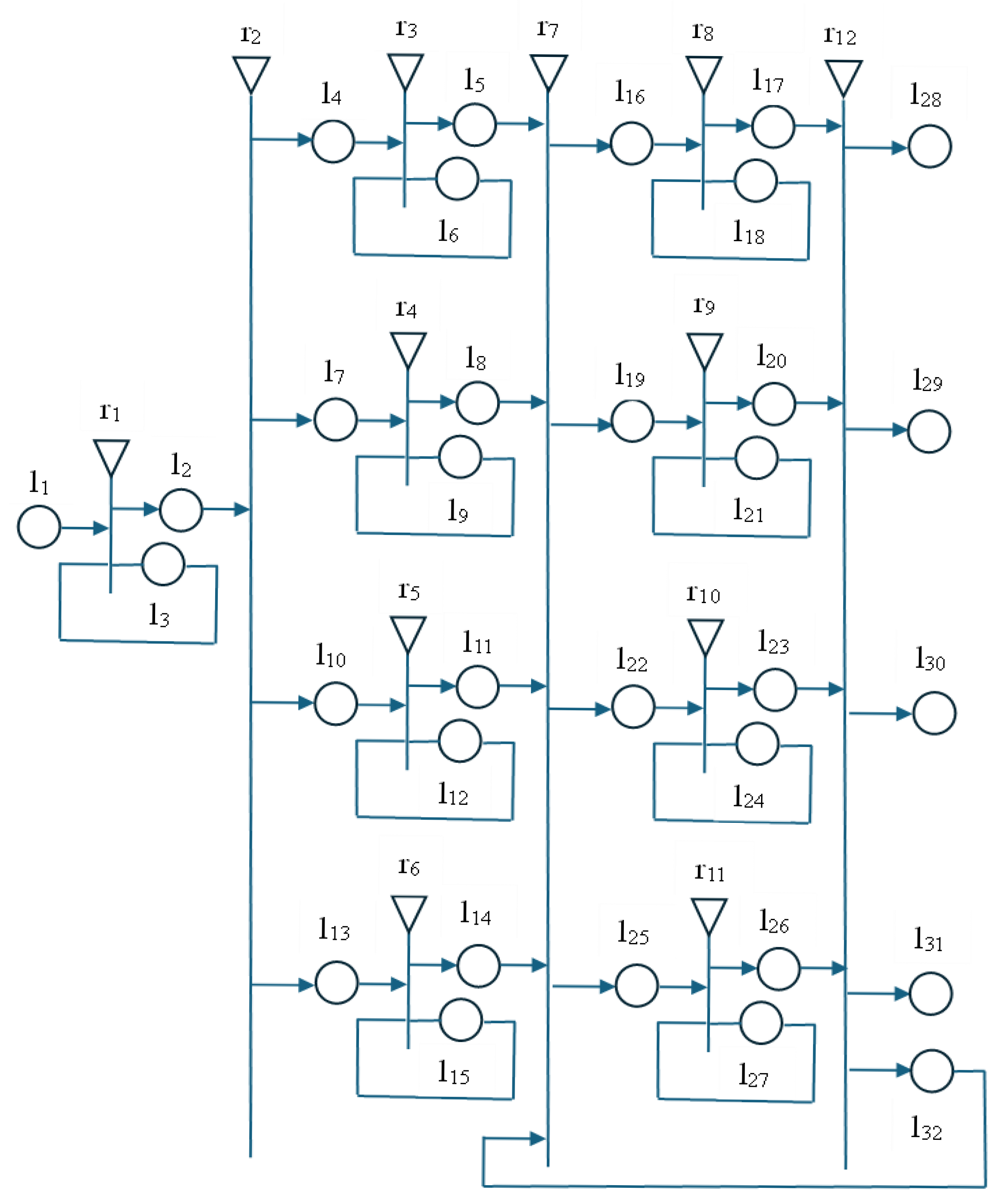
Figure 1 presents the generalized net model, with the help of which the effectiveness of the IVA, which solves various tasks in a risky environment, can be studied. IVAs, with the necessary architecture for experiments, are the tokens that move in this virtual world. The indexed transition matrices of this model are given in Figure 2. The purpose of each transition in the GNM is as follows.

r₁—token selection—an IVA GNM with the necessary architecture for experiments. For example, tokens are IVA GNM-electricians in a risky environment; IVA GNM-drones for the extinguishing of fires; and IVA GNM-electrical engineers to perform rescue operations. Boolean variables are introduced to determine the selected IVA architecture: Bool_IVA_el_technic, Bool_IVA_drone, Bool_IVA_rescue.

r₂—scenario selection—occurrence of a dangerous situation requiring evacuation. This can include the scenario of patrolling in an electrical substation; an accident requiring a rescue operation; or the training of students or specialists onsite in an electrical substation. Boolean variables corresponding to each scenario are introduced: Bool_evacuation, Bool_rescue, Bool_patrolling, Bool_student_learning.

The transitions r₃, r₄, r₅, and r₆ represent each of the four modeled scenarios. The predicates w_{6 6}, w_{9 9}, w_{12 12}, w_{15 15} refer to access to the knowledge necessary to implement these scenarios. This knowledge is represented by internal tokens for each of the given transitions, respectively. The following more important predicates are used:

W_{4 5} = Mr₃_evacuation (Bool_IVA_el_technic ˄ Bool_evacuation);

W_{7 8} = Mr₄_rescue ((Bool_IVA_rescue ˅ Bool_IVA_drone) ˄ Bool_rescue);

W_{10 11} = Mr₅_patrolling (Bool_IVA_el_technic ˄ Bool_patrolling);

W_{13 14} = Mr₆_learning (Bool_IVA_el_technic ˄ Bool_student_learning).

r₇ is a transition aimed at selecting an algorithm for the training of the IVA. The possible algorithms are the InCh-Q algorithm for machine learning, a modification of the Q-algorithm for reinforcement learning to select the most appropriate evacuation plan, SAC, PPO, GAIL, and CB. The following Boolean variables are introduced: Bool_InCh_Q, Bool_RL_evacuation, Bool_SAC, Bool_PPO, Bool_GAIL, Bool_CB.

The transitions r₈, r₉, r₁₀, and r₁₁ represent the implementation of each of the considered machine learning algorithms. The predicates w_{18 18}, w_{21 21}, w_{24 24}, and w_{27 27} refer to access to the knowledge needed to implement each of the algorithms. Some of the predicates used are as follows:

W_{16 17} = Mr₈_InCh_Q (Bool_IVA_el_technic ˄ Bool_evacuation) ˅;

Mr₈ _multy_plan_Q (Bool_IVA_el_technic ˄ Bool_evacuation);

W_{19 20} = Mr₉ _SAC ((Bool_IVA_rescue ˅ Bool_IVA_drone) ˄ Bool_rescue) ˅;

Mr₉ _PPO ((Bool_IVA_rescue ˅ Bool_IVA_drone) ˄ Bool_rescue) ˅;

Mr₉ _GAIL ((Bool_IVA_rescue ˅ Bool_IVA_drone) ˄ Bool_rescue);

W_{22 23} = Mr₁₀ _CB (Bool_IVA_el_technic ˄ Bool_patrolling) ˅;

Mr₁₀ _SAC (Bool_IVA_el_technic ˄ Bool_patrolling);

W_{25 26} = Mr₁₁_InCh_Q (Bool_IVA_el_technic ˄ Bool_student_learning).

The transition r₁₂ is used to analyze the behavior and effectiveness of intelligent agents in different algorithms and scenarios. The following Boolean variables are used: Bool_IVA_rescue_good_behavior; Bool_IVA_el_technic_good_behavior; Bool_IVA_drone_good_behavior. They are used to evaluate the behavior of the IVA. If it is not sufficient, then the training should continue. The experiments performed and the results obtained are published in [7,11,12,13].

The predicates w_{32 16}, w_{32 19}, w_{32 22}, w_{32 25} implement the continuation of the IVA training by increasing the number of training epochs with the selected algorithm and the selected scenario. The feedback allows for the continuation of the analysis of the IVA’s behavior and efficiency. An example of a used predicate is as follows:

W_{32 16} = Mr₁₂ _InCh_Q_continue_learning (¬ Bool_IVA_el_technic_good_behavior ˄ Bool_evacuation) ˅ Mr₁₂_multy_plan_Q_continue_learning (¬Bool_IVA_el_technic_good_behavior ˄ Bool_evacuation).

3. GNMs for the Behavior Study of an IVA-Electrician in a Risky Environment

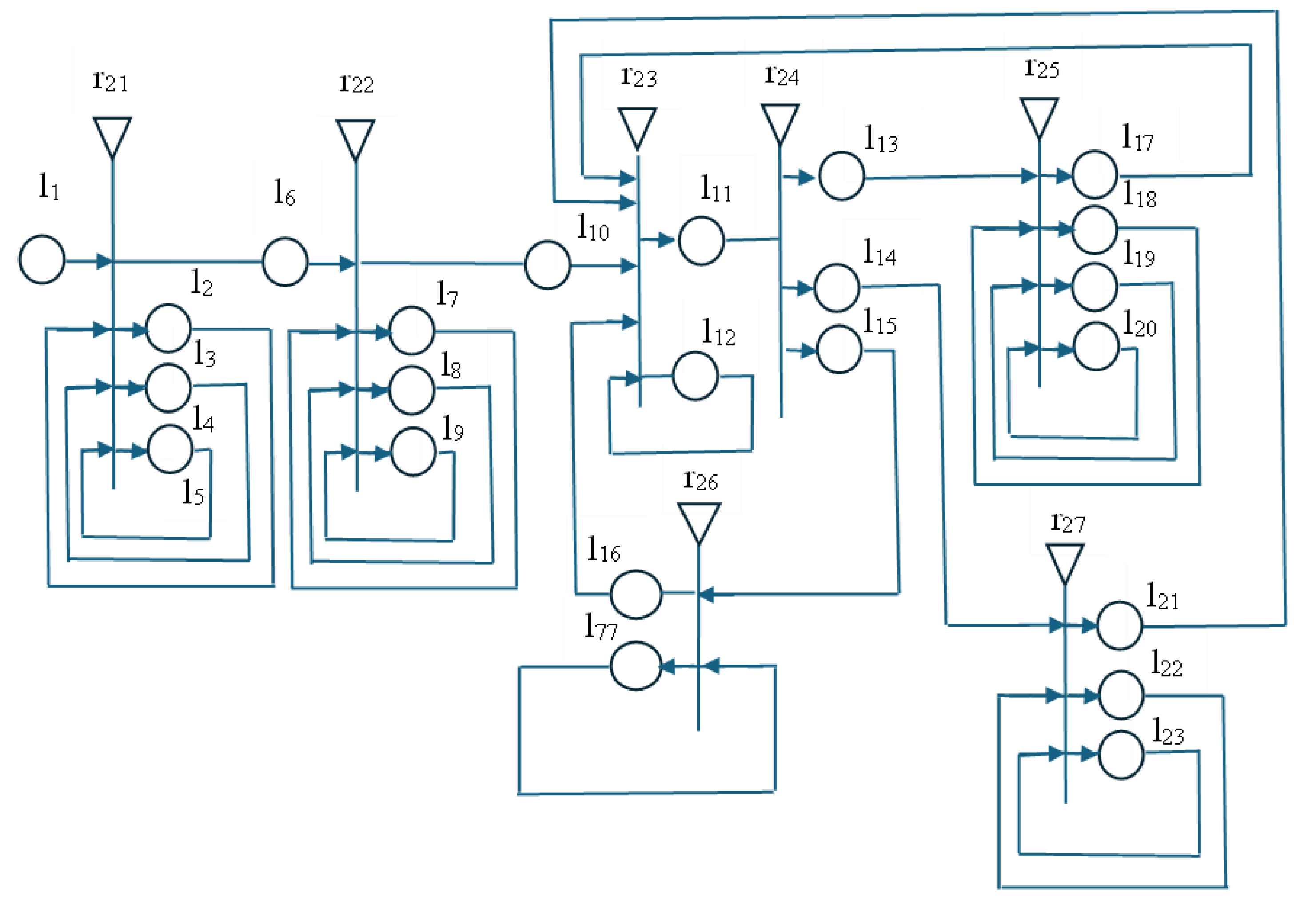
The proposed GNM for the behavior study of an IVA—an electrician in a risky environment, as given in Figure 3—covers the stage of obtaining knowledge via the IVA about the environment, emotions, needs, goals, strategies for social power, rules for social skills, and rules for changing priorities. The model represents the cases of occurrence of a dangerous situation [7], a situation in which a routine walkthrough of an electrical substation is required [12], and the case in which visitors have arrived at the electrical substation and need to be trained onsite [7]. The modified algorithms for training are modeled, in which the intensity of the disaster is set [7], and the algorithm in which the most appropriate evacuation plan is dynamically selected and with adaptive behavior is implemented [11]. The GNM shows the sequence of actions taken by the agent and the sequence of accumulation of the necessary knowledge for their implementation. The tokens that pass through this second GNM represent a model of the IVA’s memory. This memory will be enriched with knowledge and experience during the experiments.

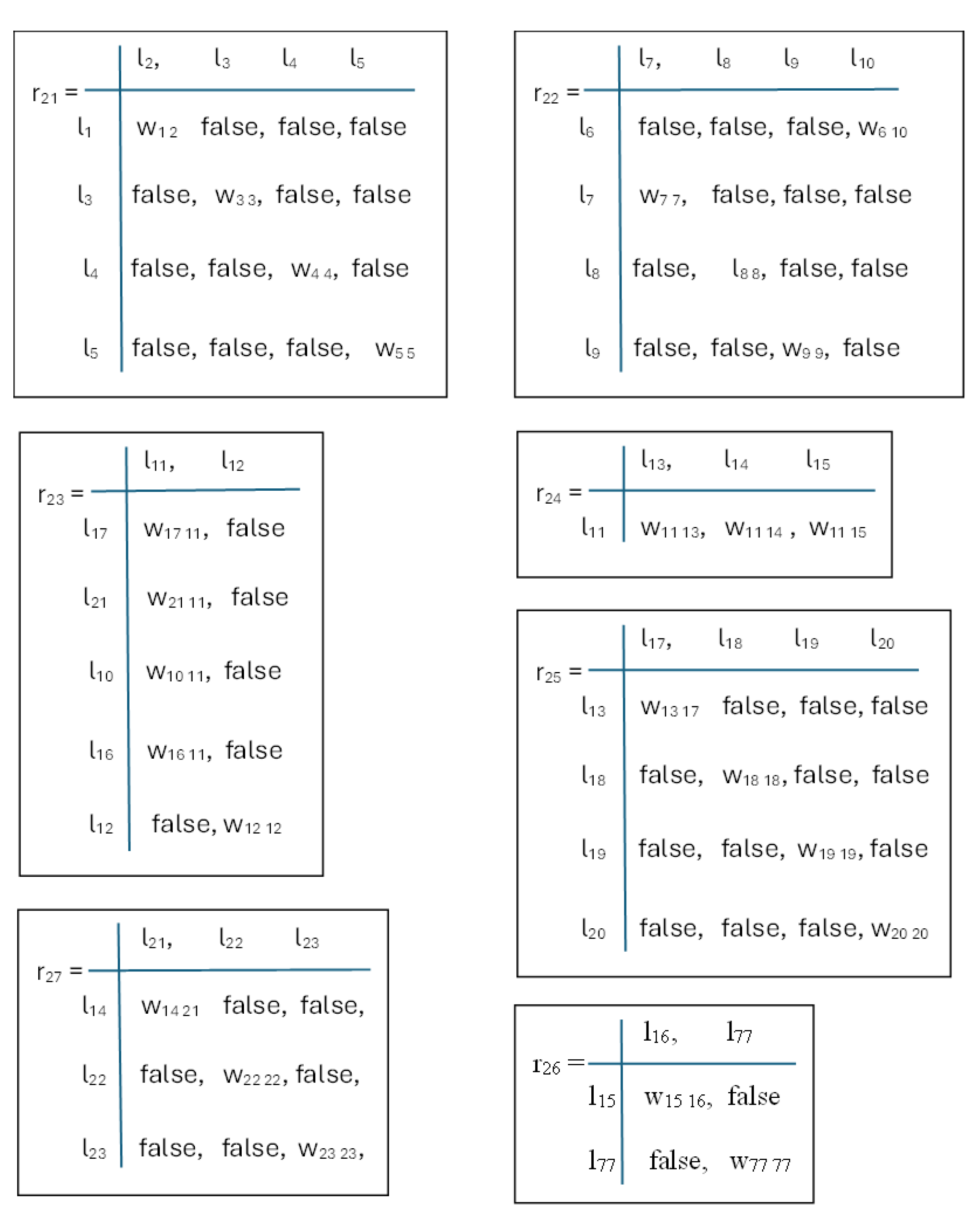
The indexed transition matrices of this model are given in Figure 4. The purpose of each transition in the proposed GNM is as follows.

The transition r₂₁ represents the possibility for an IVA-electrician to obtain knowledge about the environment according to the model of the existing open switchgear, the location of the available equipment, the technical means of protection, and the available plans. This knowledge is modeled with tokens internal to the transition itself and the predicates w_{3 3}, w_{4 4}, w_{5 5}.

r₂₂ describes the knowledge that an IVA-electrician receives about existing emotions, needs, and strategies for social power, represented by internal tokens for this transition and predicates w_{7 7}, w_{8 8}, w_{9 9}.

r₂₃ models the rules for changing priorities and goals depending on the situation, i.e., risky or safe for user training. They are implemented with internal transition tokens and predicate w_{12 12}.

r₂₄ shows the choice of one of the possible scenarios—the occurrence of a risky situation—i.e., an accident, patrolling, or the training of users in a safe environment. These scenarios can develop randomly. It is possible to switch to the development of one of the other scenarios during any scenario. This leads to a change in emotions, needs, priorities, and goals, as well as a change in behavior and the actions taken.

With the transition r ₂₅, a model of evacuation actions that must be taken in the event of an accident is implemented. The implemented algorithm for learning with stimulation, i.e., the InCh-Q algorithm [7], and the algorithm for the implementation of dynamic adaptive behavior using multiple plans [11] are considered, as well as using a decision boundary to detect injured users [14] and applying a social power strategy [7]. They are implemented with internal cores that circulate in this transition. This is implemented with the predicates w_{18 18}, w_{19 19}, w_{20 20}.

The transition r₂₆ illustrates how an IVA-electrician implemented social skills in training users who came to visit the electrical substation. This transition requires knowledge of facial expressions, gestures, and lessons that need to be explained. This knowledge is modeled with the circulation of internal cores represented by the predicate w_{77 77}.

Transition r₂₇ shows the implementation of patrolling behavior, which requires knowledge about possible problems to monitor for and how to react when they are detected. This knowledge is also modeled with internal tokens for the transition and the predicates w_{22 22}, w_{23 23}.

4. Discussion

In addition to generalized networks, there are other commonly used models for the study of the behavior of intelligent agents in a risky environment.

Classical Petri nets are the basis from which generalized networks start. They are simpler but are also useful in modeling parallel, competitive processes if the system does not require very complex parameters [15].

Discrete event systems describe processes in which, at certain discrete moments, an event occurs, which causes changes to occur. For example, such an event can be an accident, a signal, or an action performed by an agent. They are often used to model processes in traffic, factories, or logistics problems [16,17].

Finite state machines are suitable for describing agents that go through clearly defined states, such as “patrol”, “communicate”, “evacuate”, “train”, or “rescue”. They are used in robotics, games, and various simulations [18,19].

The construction of multi-agent systems is an approach that uses multiple agents that interact with each other by cooperating or competing to solve a given task. The challenge is to achieve coordination between agents, security, and efficiency in the distribution of tasks between agents [20].

Markov decision processes are powerful models that can be used to make decisions by multiple agents under uncertainty. They describe probabilistic transitions between states. They study and model how agents interact with each other. They take into account the receipt of long-term rewards and the evolution of the system over time [21,22].

Bayesian networks are used in conjunction with agent-based modeling. They are often used for decision-making based on probabilities. They allow for the quantification of uncertainty in machine learning models and increase the accuracy of predictions [23].

Bayesian neural networks have the advantage of estimating uncertainty in predictions. In them, the weights are modeled as probability distributions. This allows the network to generate a distribution of possible outcomes, rather than a single specific estimate. This also allows us to determine how confident the network is in the estimate that it has given [24].

Due to the great flexibility and efficiency of GNMs, they were chosen here to study the behavior of IVAs in a risky environment. On the other hand, however, building an appropriate and formally correct GNM that is, at the same time, understandable, practically applicable, and easy to interpret is a complex process [25]. The model must, on the one hand, reflect the complexity of the real scenario or system and, on the other hand, have acceptable computational complexity, allowing the analysis and interpretation of the obtained results. This includes several sub-problems. For example, what should be the structure of the GNM? What should be the transitions and places in the model to present the essential aspects of the system without overloading it with unnecessary details? What should be the token model? What logical, arithmetic, or algebraic expressions should be set as conditions for the tokens to pass through the transitions? How can we interpret the results to make useful decisions and improve the efficiency and find bottlenecks in the modeled systems, objects, or scenarios?

One hypothesis is that a GNM with an optimized architecture (a balanced number of transitions and places) will lead to a reduction in the computational time of the simulations without reducing the accuracy of the obtained results. The use of probabilistic indices in transitions will improve the representation of the uncertainty of the surrounding risk environment. Proving this hypothesis is a matter for future research.

Another hypothesis for future research that is put forward is that the integration of virtual reality technology, which allows for the immersive, captivating visualization of the modeled processes, will increase the interest in GNMs and facilitate the analysis of the results of the experiments conducted.

5. Conclusions

The mathematical apparatus of generalized networks is applied to represent the behavior of IVAs in a risky environment. Two GNMs are proposed, with the help of which the effectiveness and behavior of IVAs in a risky environment are studied. A model of an electrical substation is considered as a known risky environment where dynamically critical situations can arise. IVA behavior is studied in various scenarios that require the training of students, patrolling, choosing an evacuation plan, implementing a rescue operation, and extinguishing a fire. The IVA applies spatial knowledge, social behavior, emotions, and power strategies. For a comparative analysis, several machine learning algorithms, such as InCh-Q, multi-plan RL, PPO, SAC, GAIL, and CB, and the Unity modeling environment, are applied to an ML agent toolkit.

Issues related to the design and use of GNMs for the reliable modeling and analysis of the behavior and effectiveness of IVAs operating in dynamic and risky environments are discussed. The advantages and challenges of using GNMs in comparison with other classical models used to study IVA behavior are considered. For the purposes of future research, the following hypothesis is proposed: the integration of virtual reality technology, which allows for the immersive, captivating visualization of the modeled processes, will enhance the interest in GNMs and the analysis of the results of the experiments conducted.