Non-Linear Investigation of a Functionally Graded Pipe †
Abstract
1. Introduction
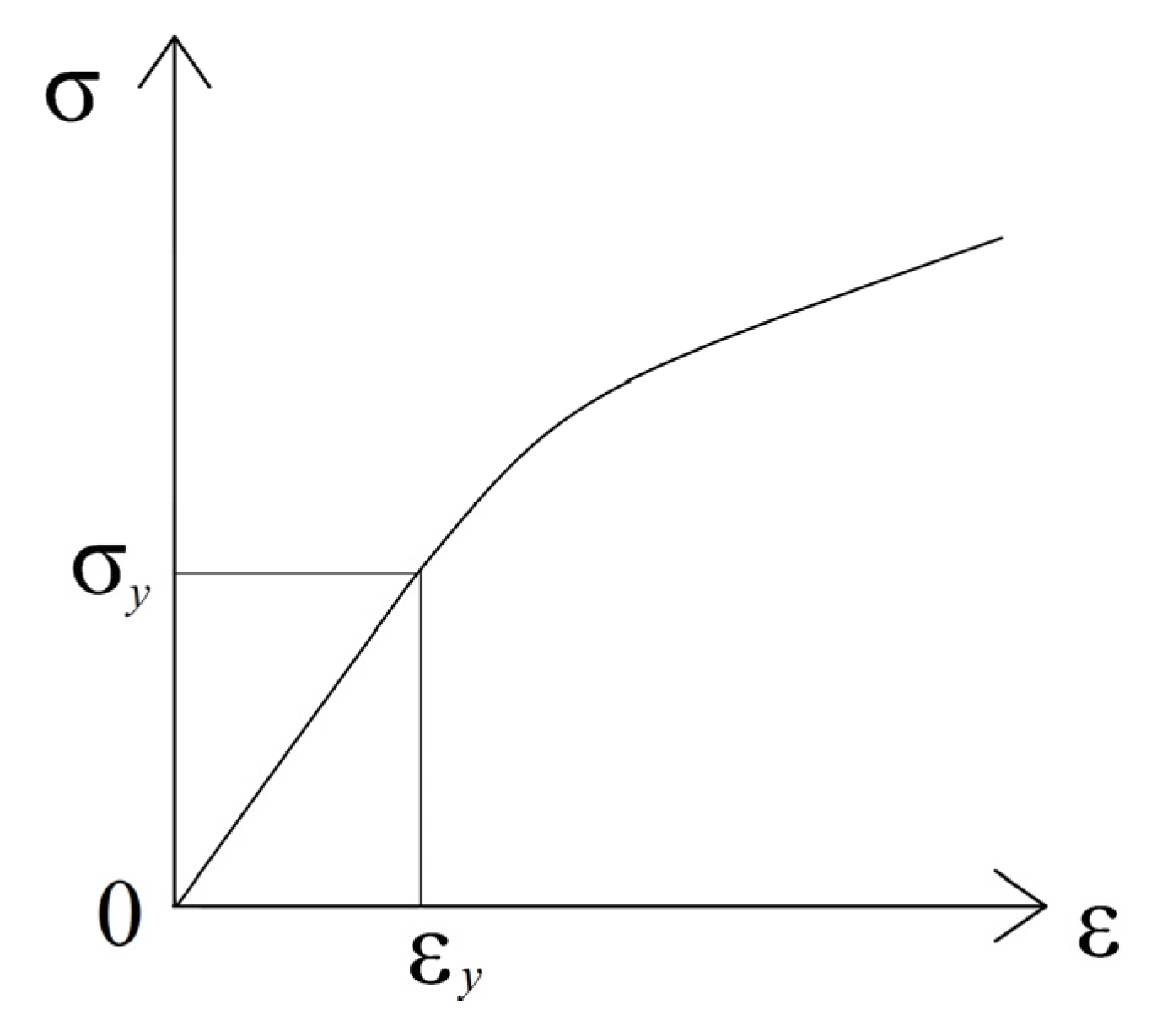
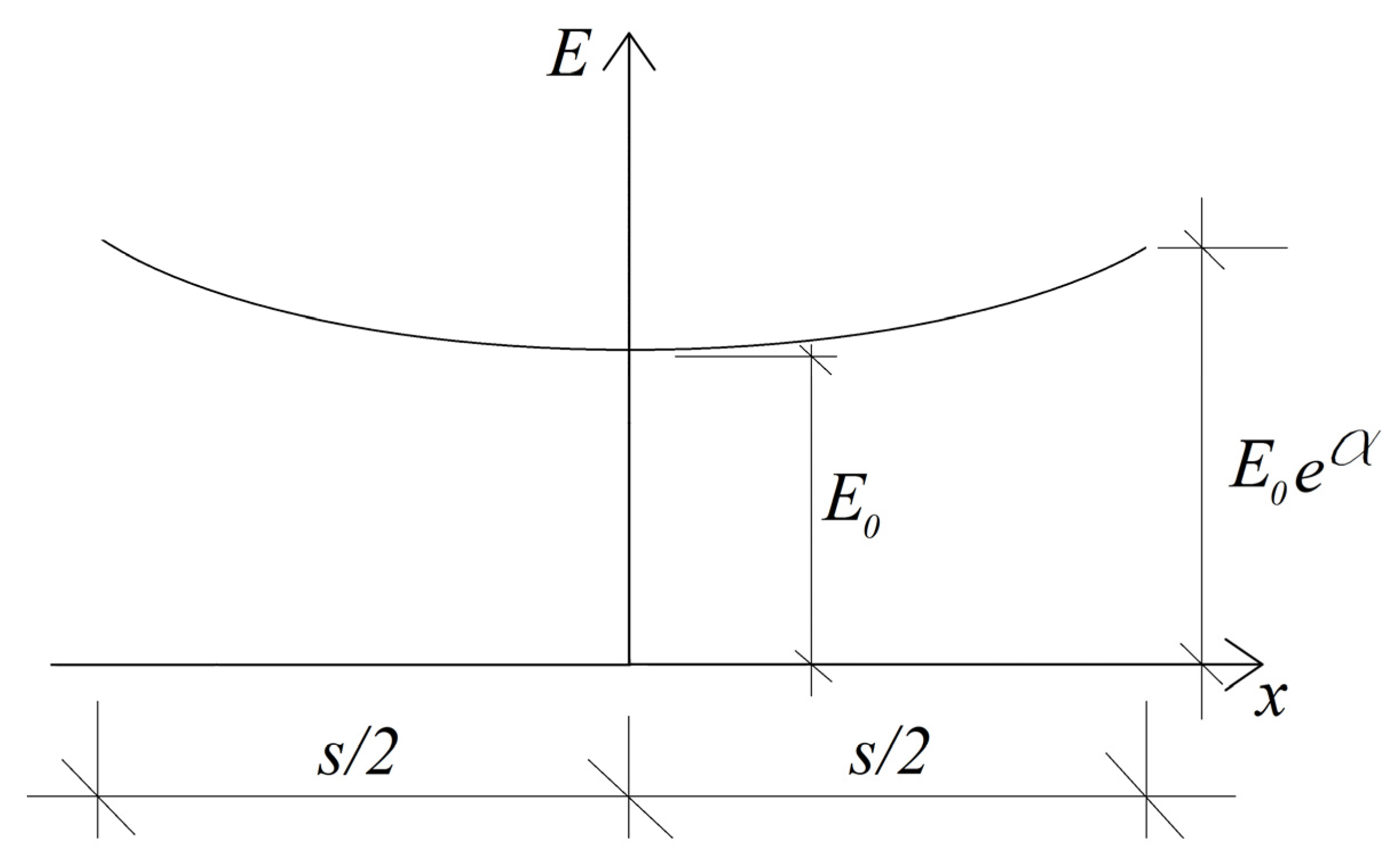
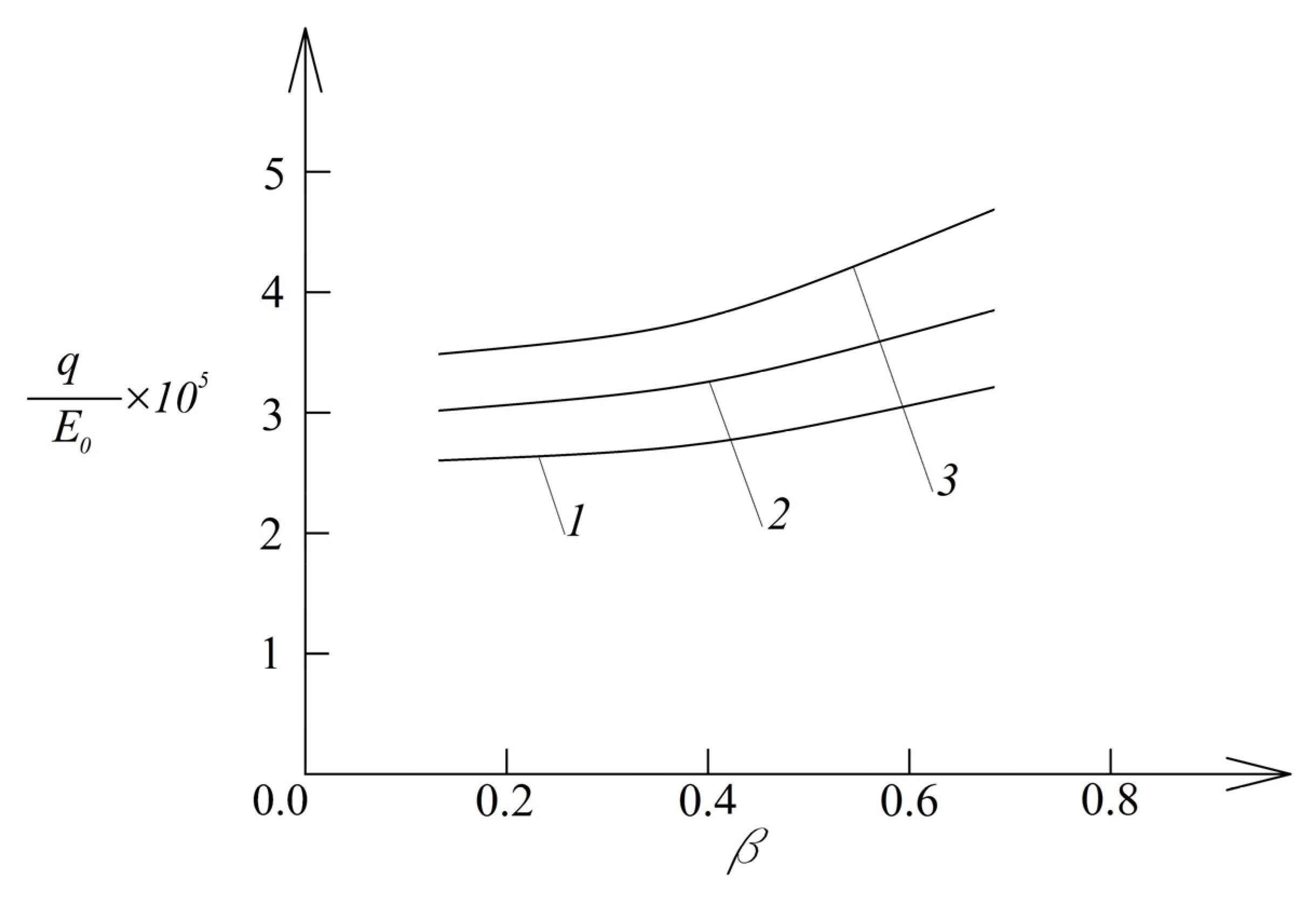
2. Pipe Non-Linear Investigation
3. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gol’Denveizer, A.L. Theory of Elastic Thin Shells: Solid and Structural Mechanics; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Ciarlet, P.G. Mathematical Elasticity: Theory of Shells; SIAM: Philadelphia, PA, USA, 2022; p. 86. [Google Scholar]
- Saada, A.S. Elasticity: Theory and Applications; Elsevier: Amsterdam, The Netherlands, 2013; p. 16. [Google Scholar]
- Feng, K.; Shi, Z.C. Mathematical Theory of Elastic Structures; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Dym, C.L. Introduction to the Theory of Shells: Structures and Solid Body Mechanics; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Hetnarski, R.B.; Ignaczak, J. The Mathematical Theory of Elasticity; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Bertram, A.; Glüge, R. Solid Mechanics; Springer: Berlin, Germany, 2015; p. 7. [Google Scholar]
- El-raheb, M. Transient response of a hollow cylinder with radial and axial material inhomogeneity. J. Acoust. Soc. Am. 2006, 119, 2738–2749. [Google Scholar] [CrossRef]
- Elishakoff, I.E.; Pentaras, D.; Gentilini, C. Mechanics of Functionally Graded Material Structures; World scientific: Singapore, 2015. [Google Scholar]
- CPM, S.A.; Varghese, B.; Baby, A. A review on functionally graded materials. Int. J. Eng. Sci 2014, 3, 90–101. [Google Scholar]
- Parihar, R.S.; Setti, S.G.; Sahu, R.K. Recent advances in the manufacturing processes of functionally graded materials: A review. Sci. Eng. Compos. Mater. 2018, 25, 309–336. [Google Scholar] [CrossRef]
- Tvergaard, V.; Needleman, A. On the Development of Localized Buckling Patterns; The Danish Center for Applied Mathematics and Mechanics: Kongens Lyngby, Denmark, 1982; Report No. 243. [Google Scholar]
- Feodosiev, V.I. Strength of Materials. Mir: Moscow, Russia, 1986. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rizov, V. Non-Linear Investigation of a Functionally Graded Pipe. Eng. Proc. 2025, 100, 4. https://doi.org/10.3390/engproc2025100004
Rizov V. Non-Linear Investigation of a Functionally Graded Pipe. Engineering Proceedings. 2025; 100(1):4. https://doi.org/10.3390/engproc2025100004
Chicago/Turabian StyleRizov, Victor. 2025. "Non-Linear Investigation of a Functionally Graded Pipe" Engineering Proceedings 100, no. 1: 4. https://doi.org/10.3390/engproc2025100004
APA StyleRizov, V. (2025). Non-Linear Investigation of a Functionally Graded Pipe. Engineering Proceedings, 100(1), 4. https://doi.org/10.3390/engproc2025100004




