A Mathematical Modeling Approach to Estimate Blood Glucose Behavior in Individuals with Prediabetes
Abstract
1. Introduction
2. Materials and Methods
- Experimental Protocol in Human Subjects: All procedures involving human participants complied with the Declaration of Helsinki, the Belmont Report, and national regulations. The study protocol was reviewed and approved by the Ethics Committee of the Faculty of Medicine, Universidad Autónoma del Estado de Morelos (Approval Code: CONBIOETICA-17-CEI-003-201-81112). Recruitment took place between August 2022 and August 2023. Informed consent was obtained from all participants, and personal data was anonymized and securely stored. Additional details on ethical and methodological procedures are provided in Supplementary Materials, Section S1.
- Experimental tests: Participants were selected and classified according to their fasting capillary glucose levels: those with values below 100 mg/dL were considered normoglycemic, while levels between 100–126 mg/dL indicated prediabetes [33]. Selected participants underwent anthropometric and body composition assessments and were implanted with an interstitial glucose sensor to allow continuous monitoring of glucose levels.
- Mathematical modeling: To start the model, a mathematical representation of glucose homeostasis was generated. Using experimental data, glucose signals were processed, and key model parameters and variables were estimated. Local minima for these parameters were then calculated, and the model was validated using correlation and error analyses, comparing measured values with model approximations.
2.1. Instrumentation
2.2. Study Population
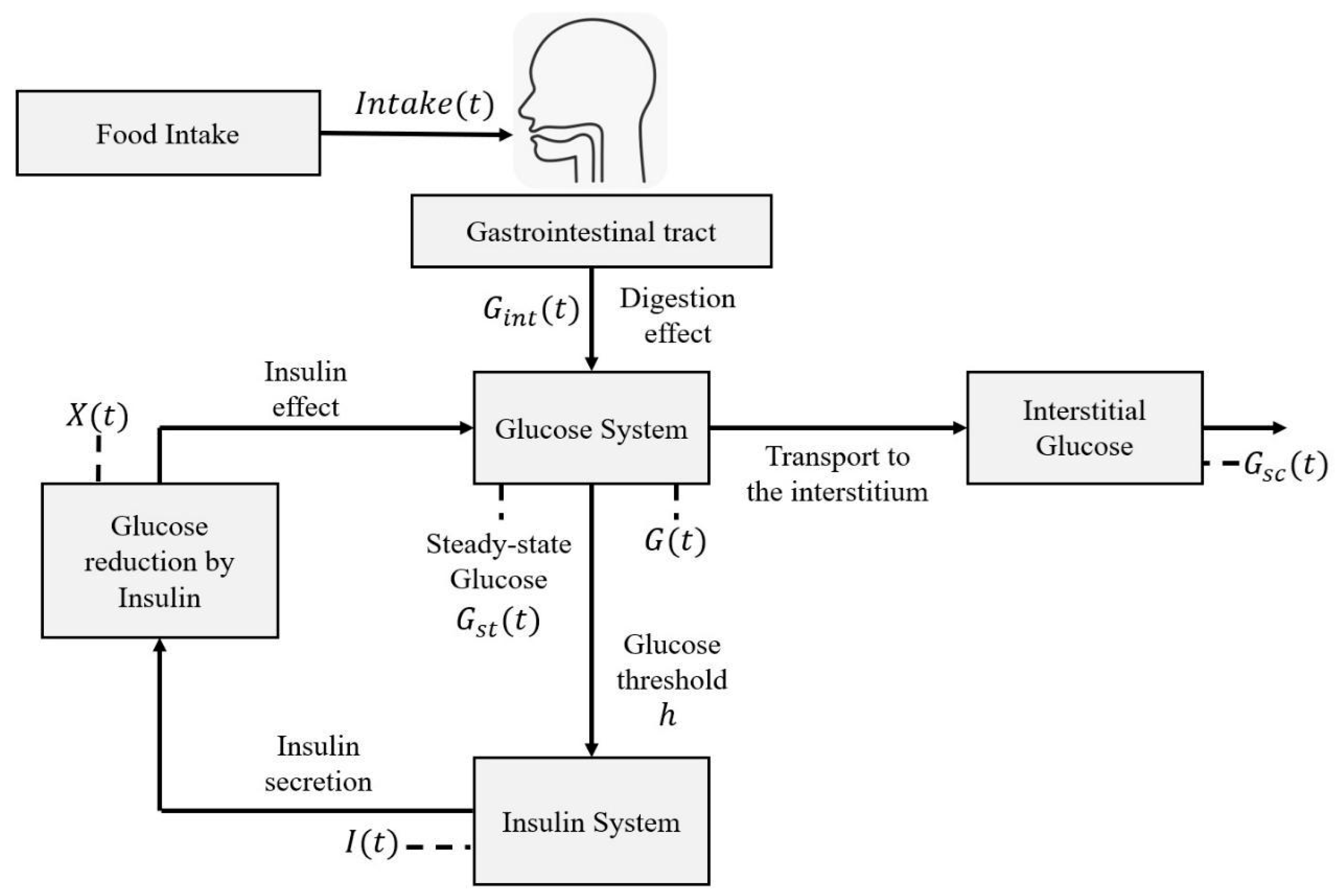
2.3. Mathematical Representation
2.3.1. Steady-State Glucose Variation
2.3.2. Circadian Cycle Effect
2.3.3. Digestion Dynamics
2.3.4. Gaussian Function as Particularity Factor
2.4. Characterization Methodology
3. Results
3.1. Signal and Parameter Estimation
- System Configuration for DEKF Estimation: The estimated states are , with parametric uncertainty addressed individually for each participant. For healthy individuals, the parameters are ; for those with prediabetes, . The system input is , and measurable outputs are . Notably, since only interstitial glucose is measured, is considered with a 15-min lead relative to , following Stout et al. [48].
- Observability Analysis and Model Conditioning: Perform observability analysis and adapt the nonlinear model to meet DEKF requirements.
- Initialization of Estimation Conditions: Define initial states (), parameters (), estimates (), noise covariance matrices (), sampling time () and apply a truncated Taylor series expansion.
- Iterative Estimation Procedure: Implement the DEKF update cycle based on the number of available system measurements.
3.2. Model Performance
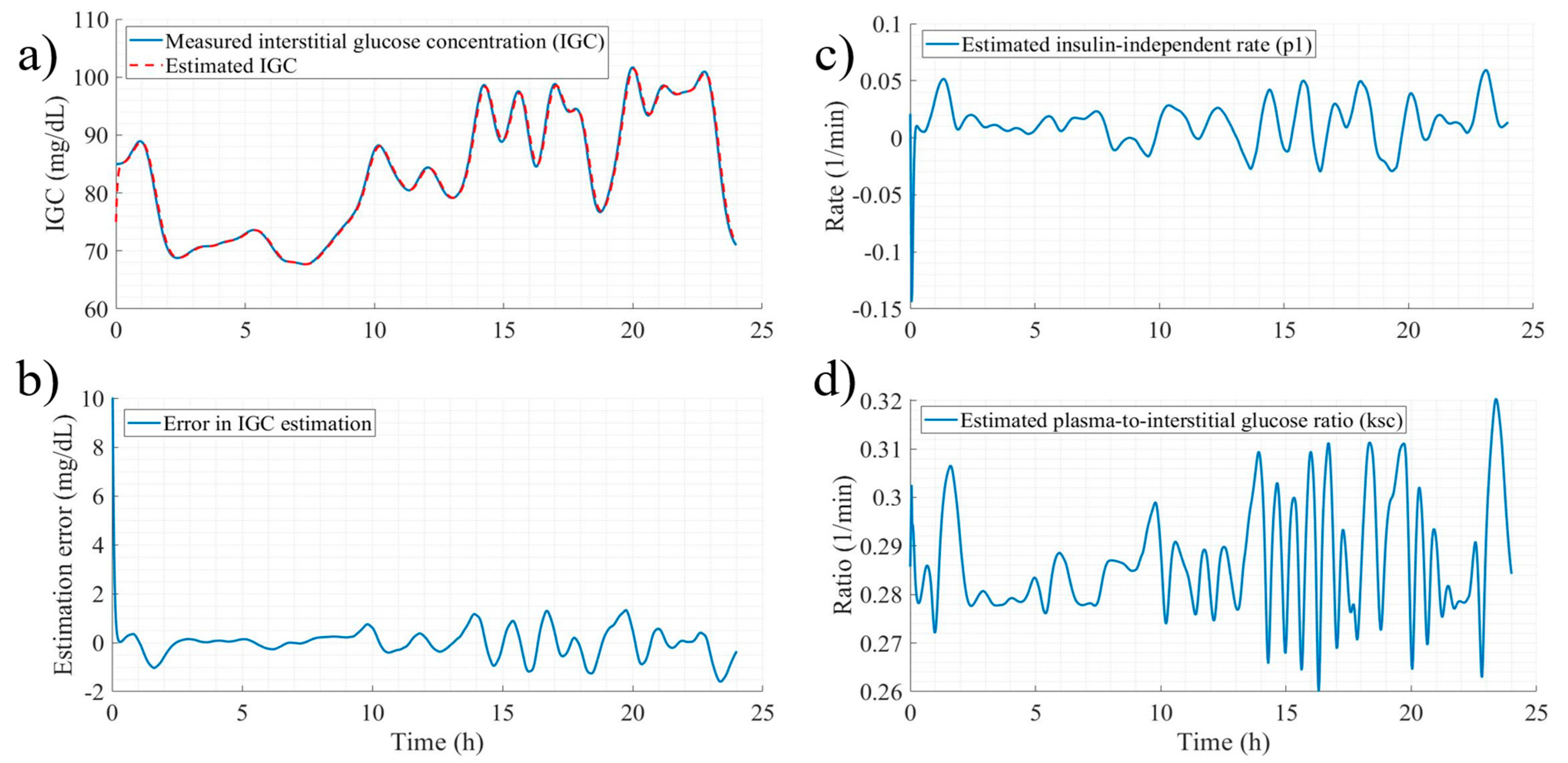
3.2.1. Performance of State Estimation
3.2.2. Model Performance with Local Minimum Values
3.2.3. Comparative Analysis Between Measured Glucose
- The first aspect highlights the real-time comparison between daily glucose measurements and model-based estimations. Panels “a” and “d” show the measured glucose (blue line) and the estimated signal (orange dashed line), selected based on median performance indices. These examples demonstrate the model’s fidelity, with only minor underestimation.
- The second aspect, shown in panels “b” and “e,” illustrates the error dynamics between measurement and estimation. These results confirm the model’s predictive capacity, with the largest deviations—typically triggered by intake events—ranging from 5 to 20 mg/dL across both profiles.
- The third aspect, shown in panels “c” and “f,” evaluates the model’s effectiveness across measurement days by comparing average glucose values from the measurements and estimates. This approach assesses the cumulative estimation error and reveals a strong positive correlation: Spearman’s r = 0.9839, p < 0.01 for healthy individuals, and r = 0.9851, p < 0.01 for those with prediabetes. We calculated correlations using MATLAB’s (version R2023b) “corr (‘Type’, ’Spearman’)” function.
3.3. Local Minima of Model Parameters
3.4. Stability of the Mathematical Model
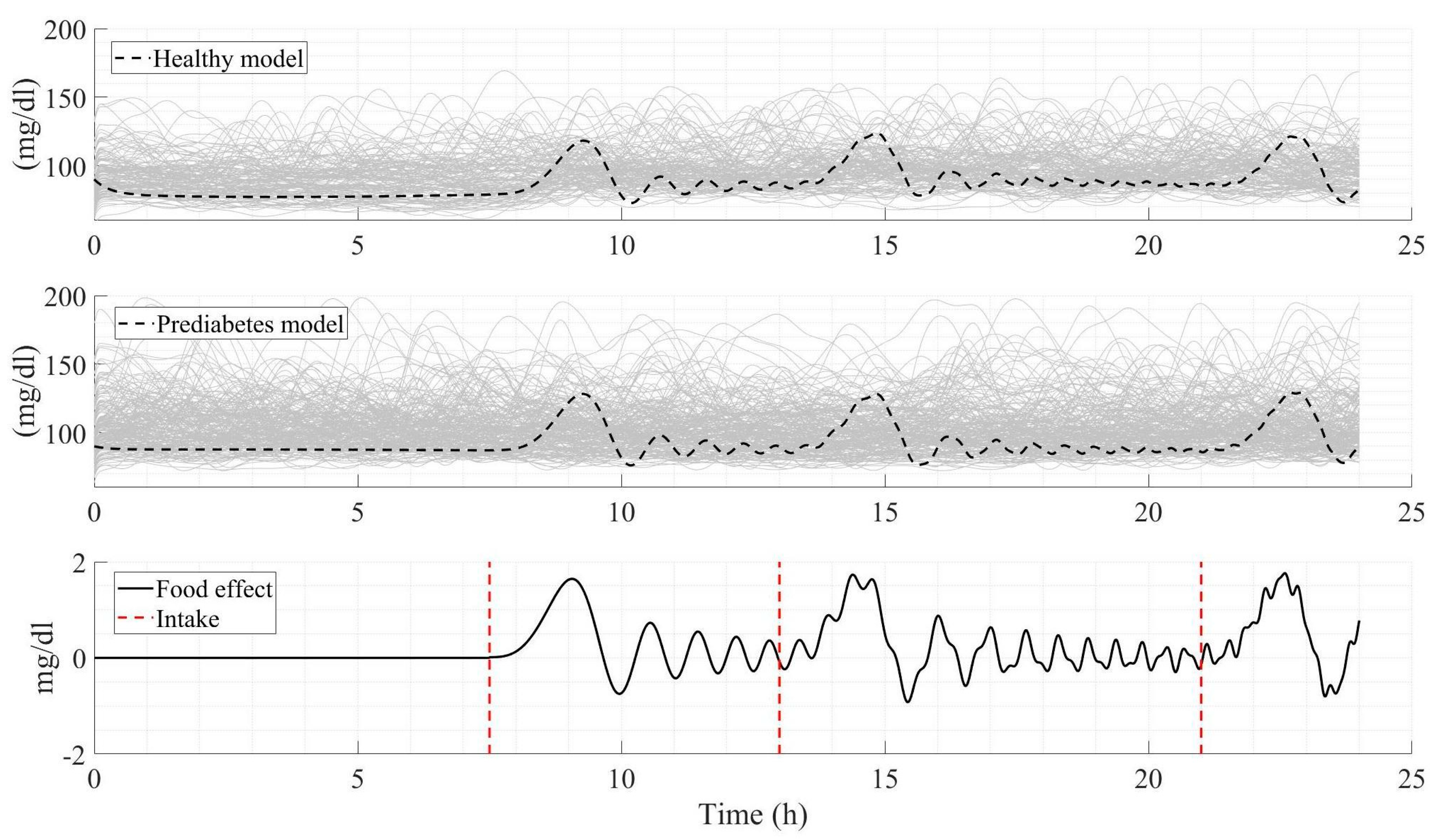
3.5. Comparative Analysis Between Measured Glucose Profiles and Model Simulation
4. Discussion
- -
- Robust extension of the classical Bergman representation
- -
- Mathematical simplicity that enables fast and efficient decision-making
- -
- Novel integration of dietary intake effects on the glucose–insulin system
- -
- Flexibility to generate individualized dynamics for virtual patients and populations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BGC | Blood glucose concentration | |
| IGC | Interstitial glucose concentration | |
| DEKF | Dual Extended Kalman Filter | |
| IAE | Integral of absolute error | |
| ISE | Integral of squared error | |
| MSE | Mean square error | |
| T1DM | Type 1 Diabetes Mellitus | |
| T2DM | Type 2 Diabetes Mellitus | |
| Symbol | Units | Description |
| System states | ||
| Blood glucose concentration | ||
| Effect of glucose lowering by insulin action | ||
| Plasma insulin concentration | ||
| Interstitial glucose concentration | ||
| Algebraic relationships | ||
| Glucose concentration at steady state | ||
| Effect of the circadian cycle on glucose | ||
| System inputs | ||
| Effect of diet on insulin-glucose variation | ||
| System parameters | ||
| mg/dL | Basal glucose concentration | |
| Basal insulin concentration | ||
| Insulin-independent constant rate | ||
| Rate of decrease in tissue glucose uptake ability | ||
| Insulin-dependent increase | ||
| Relationship between the effect of feeding on plasma glucose | ||
| Insulin release rate by β-cells | ||
| η | First-order decay rate of insulin in blood | |
| mg/dL | Glucose threshold in β-cell secretion | |
| Ratio of plasma glucose to interstitial glucose | ||
| () | Proportionality of the oscillatory signal | |
| Constant rate of the effect of food on glucose-insulin | ||
| Ratio between carbohydrates consumed and the effect on the glucose-insulin system | ||
| Polynomial coefficient 1 of the effect of the circadian cycle on glucose variation | ||
| Polynomial coefficient 2 of the effect of the circadian cycle on glucose variation | ||
| Polynomial coefficient 3 of the effect of the circadian cycle on glucose variation | ||
| Polynomial coefficient 4 of the effect of the circadian cycle on glucose variation | ||
| g | Carbohydrates consumed | |
| Bell crest in the Gaussian function | ||
| Center of the bell in the Gaussian function | ||
| Standard deviation in the bell of the Gaussian function | ||
| min | Time | |
| DEKF and Levenberg-Marquardt | ||
| - | States (System variables) | |
| - | Parameters to estimated | |
| - | State and parameter estimate | |
| - | Noise matrices in measurements and the system | |
| - | Covariance Error Matrices | |
| - | Kalman gain | |
| - | Sampling time | |
| - | Jacobians in relation to | |
| - | Transpose | |
| - | Tolerance | |
| - | Maximum number of iterations | |
| - | Combination coefficient | |
| - | Jacobians in relation to | |
| - | Error between measurements and estimations | |
References
- Kusunoki, Y.; Konishi, K.; Tsunoda, T.; Koyama, H. Significance of Glycemic Variability in Diabetes Mellitus. Intern. Med. 2022, 61, 281–290. [Google Scholar] [CrossRef]
- Taylor, S.I.; Yazdi, Z.S.; Beitelshees, A.L. Pharmacological treatment of hyperglycemia in type 2 diabetes. J. Clin. Investig. 2021, 131, e142243. [Google Scholar] [CrossRef]
- Stinson, S.E.; Jonsson, A.E.; de Retana Alzola, I.F.; Lund, M.A.V.; Frithioff-Bojsoe, C.; Aas Holm, L.; Fonvig, C.E.; Pedersen, O.; Angquist, L.; Sorensen, T.I.A.; et al. Hyperglucagonemia in Pediatric Adiposity Associates with Cardiometabolic Risk Factors but Not Hyperglycemia. J. Clin. Endocrinol. Metab. 2022, 107, 1569–1576. [Google Scholar] [CrossRef] [PubMed]
- Hatamoto, Y.; Tanoue, Y.; Yoshimura, E.; Matsumoto, M.; Hayashi, T.; Ogata, H.; Tanaka, S.; Tanaka, H.; Higaki, Y. Delayed Eating Schedule Raises Mean Glucose Levels in Young Adult Males: A Randomized Controlled Cross-Over Trial. J. Nutr. 2023, 153, 1029–1037. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Zhang, P.; Ding, B.; Cao, X.; Zhong, Y.; Lee, K.O.; Ma, J.H. Response of blood glucose and GLP-1 to different food temperature in normal subject and patients with type 2 diabetes. Nutr. Diabetes 2022, 12, 28. [Google Scholar] [CrossRef] [PubMed]
- Trim, W.V.; Walhin, J.P.; Koumanov, F.; Turner, J.E.; Shur, N.F.; Simpson, E.J.; Macdonald, I.A.; Greenhaff, P.L.; Thompson, D. The impact of physical inactivity on glucose homeostasis when diet is adjusted to maintain energy balance in healthy, young males. Clin. Nutr. 2023, 42, 532–540. [Google Scholar] [CrossRef]
- Sunena; Mishra, D.N. Stress Etiology of Type 2 Diabetes. Curr. Diabetes Rev. 2022, 18, e240222201413. [Google Scholar] [CrossRef]
- Eom, Y.S.; Wilson, J.R.; Bernet, V.J. Links between Thyroid Disorders and Glucose Homeostasis. Diabetes Metab. J. 2022, 46, 239–256. [Google Scholar] [CrossRef]
- Ceriello, A. Hyperglycemia and the worse prognosis of COVID-19. Why a fast blood glucose control should be mandatory. Diabetes Res. Clin. Pract. 2020, 163, 108186. [Google Scholar] [CrossRef]
- Papachristoforou, E.; Lambadiari, V.; Maratou, E.; Makrilakis, K. Association of Glycemic Indices (Hyperglycemia, Glucose Variability, and Hypoglycemia) with Oxidative Stress and Diabetic Complications. J. Diabetes Res. 2020, 2020, 7489795. [Google Scholar] [CrossRef]
- Gilon, P. The Role of alpha-Cells in Islet Function and Glucose Homeostasis in Health and Type 2 Diabetes. J. Mol. Biol. 2020, 432, 1367–1394. [Google Scholar] [CrossRef] [PubMed]
- Sasaki, N.; Ozono, R.; Higashi, Y.; Maeda, R.; Kihara, Y. Association of Insulin Resistance, Plasma Glucose Level, and Serum Insulin Level with Hypertension in a Population with Different Stages of Impaired Glucose Metabolism. J. Am. Heart Assoc. 2020, 9, e015546. [Google Scholar] [CrossRef]
- Iacobini, C.; Vitale, M.; Pesce, C.; Pugliese, G.; Menini, S. Diabetic Complications and Oxidative Stress: A 20-Year Voyage Back in Time and Back to the Future. Antioxidants 2021, 10, 727. [Google Scholar] [CrossRef]
- Paul, S.; Ali, A.; Katare, R. Molecular complexities underlying the vascular complications of diabetes mellitus—A comprehensive review. J. Diabetes Complicat. 2020, 34, 107613. [Google Scholar] [CrossRef]
- Gallardo-Rincon, H.; Cantoral, A.; Arrieta, A.; Espinal, C.; Magnus, M.H.; Palacios, C.; Tapia-Conyer, R. Review: Type 2 diabetes in Latin America and the Caribbean: Regional and country comparison on prevalence, trends, costs and expanded prevention. Prim. Care Diabetes 2021, 15, 352–359. [Google Scholar] [CrossRef]
- O’Connell, J.M.; Manson, S.M. Understanding the Economic Costs of Diabetes and Prediabetes and What We May Learn About Reducing the Health and Economic Burden of These Conditions. Diabetes Care 2019, 42, 1609–1611. [Google Scholar] [CrossRef]
- Williams, R.; Karuranga, S.; Malanda, B.; Saeedi, P.; Basit, A.; Besancon, S.; Bommer, C.; Esteghamati, A.; Ogurtsova, K.; Zhang, P.; et al. Global and regional estimates and projections of diabetes-related health expenditure: Results from the International Diabetes Federation Diabetes Atlas, 9th edition. Diabetes Res. Clin. Pract. 2020, 162, 108072. [Google Scholar] [CrossRef]
- Ogurtsova, K.; Guariguata, L.; Barengo, N.C.; Ruiz, P.L.; Sacre, J.W.; Karuranga, S.; Sun, H.; Boyko, E.J.; Magliano, D.J. IDF diabetes Atlas: Global estimates of undiagnosed diabetes in adults for 2021. Diabetes Res. Clin. Pract. 2022, 183, 109118. [Google Scholar] [CrossRef]
- Forouhi, N.G.; Wareham, N.J. Epidemiology of diabetes. Medicine 2019, 47, 22–27. [Google Scholar] [CrossRef]
- Gruss, S.M.; Nhim, K.; Gregg, E.; Bell, M.; Luman, E.; Albright, A. Public Health Approaches to Type 2 Diabetes Prevention: The US National Diabetes Prevention Program and Beyond. Curr. Diabetes Rep. 2019, 19, 78. [Google Scholar] [CrossRef] [PubMed]
- White, M.; Barquera, S. Mexico Adopts Food Warning Labels, Why Now? Health Syst. Reform 2020, 6, e1752063. [Google Scholar] [CrossRef]
- Yang, B.; Sherman, A.S. Crafting Mathematical Models for Type 2 Diabetes Progression: Leveraging Longitudinal Data. bioRxiv 2025. [Google Scholar] [CrossRef]
- Leal, J.; Morrow, L.M.; Khurshid, W.; Pagano, E.; Feenstra, T. Decision models of prediabetes populations: A systematic review. Diabetes Obes. Metab. 2019, 21, 1558–1569. [Google Scholar] [CrossRef]
- Ha, J.; Sherman, A. Type 2 diabetes: One disease, many pathways. Am. J. Physiol. Endocrinol. Metab. 2020, 319, E410–E426. [Google Scholar] [CrossRef]
- Omana, J.; Moorthi, M. Predictive Analysis and Prognostic Approach of Diabetes Prediction with Machine Learning Techniques. Wirel. Pers. Commun. 2022, 127, 465–478. [Google Scholar] [CrossRef]
- Alonso-Bastida, A.; Adam-Medina, M.; Posada-Gomez, R.; Salazar-Pina, D.A.; Osorio-Gordillo, G.L.; Vela-Valdes, L.G. Dynamic of Glucose Homeostasis in Virtual Patients: A Comparison between Different Behaviors. Int. J. Environ. Res. Public Health 2022, 19, 716. [Google Scholar] [CrossRef] [PubMed]
- Alonso-Bastida, A.; Salazar-Pina, D.A.; Adam-Medina, M.; Ramos-Garcia, M.L. Socioeconomic Level and the Relationship in Glycemic Behavior in the Mexican Population. A Nutritional Alternative Focused on Vulnerable Populations. J. Community Health 2023, 48, 687–697. [Google Scholar] [CrossRef] [PubMed]
- Sala-Mira, I.; Garcia, P.; Diez, J.L.; Bondia, J. Internal model control based module for the elimination of meal and exercise announcements in hybrid artificial pancreas systems. Comput. Methods Programs Biomed. 2022, 226, 107061. [Google Scholar] [CrossRef]
- Misquith, A.; Rangareddy, H.; Chikkanarayanappa, V.; Sultana, A.; Ashakiran, S. Mathematical model for assessing glycemic control in type 2 diabetes mellitus. Bioinformation 2024, 20, 116–120. [Google Scholar] [CrossRef] [PubMed]
- Orozco-Lopez, O.; Rodriguez-Herrero, A.; Castaneda, C.E.; Garcia-Saez, G.; Elena Hernando, M. Method to generate a large cohort in-silico for type 1 diabetes. Comput. Methods Programs Biomed. 2020, 193, 105523. [Google Scholar] [CrossRef]
- Mughal, I.S.; Patanè, L.; Xibilia, M.G.; Caponetto, R. Variable structure-based controllers applied to the modified Hovorka model for type 1 diabetes. Int. J. Dyn. Control 2023, 11, 3159–3175. [Google Scholar] [CrossRef]
- Hovorka, R.; Canonico, V.; Chassin, L.J.; Haueter, U.; Massi-Benedetti, M.; Orsini Federici, M.; Pieber, T.R.; Schaller, H.C.; Schaupp, L.; Vering, T.; et al. Nonlinear model predictive control of glucose concentration in subjects with type 1 diabetes. Physiol. Meas. 2004, 25, 905–920. [Google Scholar] [CrossRef] [PubMed]
- American Diabetes Association Professional Practice Committee. 2. Diagnosis and Classification of Diabetes: Standards of Care in Diabetes-2024. Diabetes Care 2024, 47, S20–S42. [Google Scholar] [CrossRef]
- Kaveh, P.; Shtessel, Y.B. Blood Glucose Regulation via Double Loop Higher Order Sliding Mode Control and Multiple Sampling Rate. In Modern Sliding Mode Control Theory; Lecture Notes in Control and Information Sciences; Elsevier: Amsterdam, The Netherlands, 2008; Volume 375, pp. 427–445. [Google Scholar] [CrossRef]
- Mansell, E.J.; Docherty, P.D.; Fisk, L.M.; Chase, J.G. Estimation of secondary effect parameters in glycaemic dynamics using accumulating data from a virtual type 1 diabetic patient. Math. Biosci. 2015, 266, 108–117. [Google Scholar] [CrossRef]
- Chen, C.L.; Tsai, H.W. Modeling the physiological glucose-insulin system on normal and diabetic subjects. Comput. Methods Programs Biomed. 2010, 97, 130–140. [Google Scholar] [CrossRef]
- Rodriguez-Herrero, A.; Perez-Gandia, C.; Rigla, M.; de Leiva, A.; Gomez, E.J.; Hernando, M.E. A simulation study of an inverse controller for closed- and semiclosed-loop control in type 1 diabetes. Diabetes Technol. Ther. 2010, 12, 95–104. [Google Scholar] [CrossRef]
- Alonso-Bastida, A.; Adam-Medina, M.; Salazar-Pina, D.A.; Escobar-Jimenez, R.F.; Parra-Cabrera, M.S.; Cervantes-Bobadilla, M. Impact on Glycemic Variation Caused by a Change in the Dietary Intake Sequence. Foods 2023, 12, 1055. [Google Scholar] [CrossRef]
- Hinshaw, L.; Schiavon, M.; Mallad, A.; Man, C.D.; Basu, R.; Bharucha, A.E.; Cobelli, C.; Carter, R.E.; Basu, A.; Kudva, Y.C. Effects of delayed gastric emptying on postprandial glucose kinetics, insulin sensitivity, and β-cell function. Am. J. Physiol.-Endocrinol. Metab. 2014, 307, E494–E502. [Google Scholar] [CrossRef]
- Zannidi, D.; Methven, L.; Woodside, J.V.; McKenna, G.; Forde, C.G.; Jackson, K.G.; Shafat, A.; Schimmel, M.; Clegg, M. Variations in oral performance and processing behaviours among older adults: Associations with gastric emptying, postprandial glucose and insulin responses. Exp. Gerontol. 2025, 211, 112893. [Google Scholar] [CrossRef]
- Alonso-Bastida, A.; Franco-Nava, M.A.; Adam-Medina, M.; López-Zapata, B.; Álvarez-Gutiérrez, P.E.; García-Morales, J. Mathematical modeling of thermal interactions in a self-cooling pilot-scale photobioreactor. Case Stud. Therm. Eng. 2022, 31, 101825. [Google Scholar] [CrossRef]
- Xu, W.; Wang, S.; Jiang, C.; Fernandez, C.; Yu, C. A novel adaptive dual extended Kalman filtering algorithm for the Li-ion battery state of charge and state of health co-estimation. Int. J. Energy Res. 2021, 45, 14592–14602. [Google Scholar] [CrossRef]
- Wu, M.; Qin, L.; Wu, G. State of charge estimation of power lithium-ion battery based on an adaptive time scale dual extend Kalman filtering. J. Energy Storage 2021, 39, 102535. [Google Scholar] [CrossRef]
- Park, J.; Lee, M.; Kim, G.; Park, S.; Kim, J. Integrated Approach Based on Dual Extended Kalman Filter and Multivariate Autoregressive Model for Predicting Battery Capacity Using Health Indicator and SOC/SOH. Energies 2020, 13, 2138. [Google Scholar] [CrossRef]
- Wang, W.; Xu, X.; Yan, Z.; Wang, H. An online optimization method for extracting parameters of multi-parameter PV module model based on adaptive Levenberg-Marquardt algorithm. Energy Convers. Manag. 2021, 245, 114611. [Google Scholar] [CrossRef]
- Rubio, J. Stability Analysis of the Modified Levenberg–Marquardt Algorithm for the Artificial Neural Network Training. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 3510–3524. [Google Scholar] [CrossRef] [PubMed]
- Umar, A.O.; Sulaiman, I.M.; Mamat, M.; Waziri, M.Y.; Zamri, N. On damping parameters of Levenberg-Marquardt algorithm for nonlinear least square problems. J. Phys. Conf. Ser. 2020, 1734, 1734. [Google Scholar] [CrossRef]
- Stout, P.J.; Peled, N.; Erickson, B.J.; Hilgers, M.E.; Racchini, J.R.; Hoegh, T.B. Comparison of glucose levels in dermal interstitial fluid and finger capillary blood. Diabetes Technol. Ther. 2001, 3, 81–90. [Google Scholar] [CrossRef] [PubMed]
- Khalil, H.K. Nolinear Systems, 3rd ed.; Prentice Hall: Hoboken, NJ, USA, 2002. [Google Scholar]
- Li, J.; Zhou, J.; Chen, B. Review of wind power scenario generation methods for optimal operation of renewable energy systems. Appl. Energy 2020, 280, 115992. [Google Scholar] [CrossRef]
- Neatpisarnvanit, C.; Boston, J.R. Estimation of plasma insulin from plasma glucose. IEEE Trans. Biomed. Eng. 2002, 49, 1253–1259. [Google Scholar] [CrossRef]
- Dalla Man, C.; Rizza, R.A.; Cobelli, C. Meal simulation model of the glucose-insulin system. IEEE Trans. Biomed. Eng. 2007, 54, 1740–1749. [Google Scholar] [CrossRef]
- Lopez-Palau, N.E.; Olais-Govea, J.M. Mathematical model of blood glucose dynamics by emulating the pathophysiology of glucose metabolism in type 2 diabetes mellitus. Sci. Rep. 2020, 10, 12697. [Google Scholar] [CrossRef] [PubMed]
- Visentin, R.; Cobelli, C.; Dalla Man, C. The Padova Type 2 Diabetes Simulator from Triple-Tracer Single-Meal Studies: In Silico Trials Also Possible in Rare but Not-So-Rare Individuals. Diabetes Technol. Ther. 2020, 22, 892–903. [Google Scholar] [CrossRef] [PubMed]
- Visentin, R.; Campos-Nanez, E.; Schiavon, M.; Lv, D.; Vettoretti, M.; Breton, M.; Kovatchev, B.P.; Dalla Man, C.; Cobelli, C. The UVA/Padova Type 1 Diabetes Simulator Goes from Single Meal to Single Day. J. Diabetes Sci. Technol. 2018, 12, 273–281. [Google Scholar] [CrossRef] [PubMed]
- Stefan, N.; Fritsche, A.; Schick, F.; Haring, H.U. Phenotypes of prediabetes and stratification of cardiometabolic risk. Lancet Diabetes Endocrinol. 2016, 4, 789–798. [Google Scholar] [CrossRef]
- Qiu, S.; Cai, X.; Zhou, X.; Xu, J.; Sun, Z.; Guo, H.; Wu, T. Muscle Quality in Relation to Prediabetes Phenotypes: A Population-Based Study with Mediation Analysis. J. Clin. Endocrinol. Metab. 2024, 109, e1151–e1158. [Google Scholar] [CrossRef]
- Kulcu, E.; Tamada, J.A.; Reach, G.; Potts, R.O.; Lesho, M.J. Physiological differences between interstitial glucose and blood glucose measured in human subjects. Diabetes Care 2003, 26, 2405–2409. [Google Scholar] [CrossRef]
- Keenan, D.B.; Mastrototaro, J.J.; Voskanyan, G.; Steil, G.M. Delays in minimally invasive continuous glucose monitoring devices: A review of current technology. J. Diabetes Sci. Technol. 2009, 3, 1207–1214. [Google Scholar] [CrossRef]
- Orozco-Lopez, J.O.; Castaneda, C.E.; Rodriguez-Herrero, A.; Garcia-Saez, G.; Hernando, E. Linear Time-Varying Luenberger Observer Applied to Diabetes. IEEE Access 2018, 6, 23612–23625. [Google Scholar] [CrossRef]
- Gonzalez, A.A.; Voos, H.; Darouach, M. Glucose-Insulin System Based on Minimal Model: A Realistic Approach. In Proceedings of the UKSim-AMSS 17th International Conference on Computer Modelling and Simulation, UKSim 2015, Cambridge, UK, 25–27 March 2015; pp. 55–60. [Google Scholar] [CrossRef]
- Wan, E.A.; Nelson, A.T. Dual Extended Kalman Filter Methods. In Kalman Filtering and Neural Networks; Wiley: Hoboken, NJ, USA, 2003. [Google Scholar] [CrossRef]
- D’ Hères, S.M. and Gildas Besancon. Nonlinear Observers and Applications: Preface. In Lecture Notes in Control and Information Sciences; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar] [CrossRef]
- Hermann, R.; Krener, A.J. Nonlinear Controllability and Observability. IEEE Trans. Autom. Control 1977, 22, 728–740. [Google Scholar] [CrossRef]

| Dual Extended Kalman Filter Estimation with Parameter Variation | System Variables | |||
| , mg/dL | , mg/dL | |||
| Healthy | Healthy | |||
| IAE: 883.9 (427.5, 1759.2) | IAE: 682.9 (327.8, 1297.1) | |||
| ISE: 1981.3 (520.3, 6637.5) | ISE: 1257.5 (409.9, 3627.0) | |||
| MSE: 2.1 (0.5, 7.0) | MSE: 1.3 (0.4, 3.8) | |||
| Prediabetes | Prediabetes | |||
| IAE: 967.5 (146.1, 1740.7) | IAE: 793.5 (114.1, 1380.9) | |||
| ISE: 2255.6 (286.0, 5533.9) | ISE: 1583.9 (278.1, 3735.6) | |||
| MSE: 2.3 (0.3, 5.8) | MSE: 1.6 (0.2, 3.9) | |||
| Estimation of the proposed model with local minimum parameters | System Variables | |||
| , mg/dL | , 1/min | , mU/dL | , mg/dL | |
| Healthy | Healthy | Healthy | Healthy | |
| IAE: 2249.8 | IAE: 3.6 × | IAE: 850.4 | IAE: 882.8 | |
| (933.9, 4770.3) | (1.3 × , 7.3 × ) | (312.7, 1534.8) | (423.8, 1666.5) | |
| ISE: 8997.9 | ISE: 2.5 × | ISE: 1847.1 | ISE: 2119.9 | |
| (1882.2, 2.8 × ) | (3.7 × 7.8 × ) | (237.4, 5854.3) | (650.7, 7213.4) | |
| MSE: 9.5 | MSE: 2.7 × | MSE: 1.9 | MSE: 2.2 | |
| (2.0, 30.6) | (3.9 × 8.3 × ) | (0.2, 6.2) | (0.6, 7.6) | |
| Prediabetes | Prediabetes | Prediabetes | Prediabetes | |
| IAE: 5533.4 | IAE: 1.6 | IAE: 1191.0 | IAE: 2391.5 | |
| (1819.0, 10,315.0) | (0.7, 3.7) | (428.4, 3059.8) | (263.3, 4287.9) | |
| ISE: 6.5 × | ISE: 5.6 × | ISE: 3876.5 | ISE: 1.3 × | |
| (8.9 × , 2.1 × ) | (1.3 × , 2.3 × ) | (400.2, 2.0 × ) | (222.8, 4.6 × ) | |
| MSE: 69.1 | MSE: 5.9 × | MSE: 4.1 | MSE: 14.7 | |
| (9.5, 224.3) | (1.3 × , 2.4 × ) | (0.4, 22.1) | (0.2, 49.3) | |
| Process | Parameter, (Units) | Healthy 1 | Prediabetes 2 |
|---|---|---|---|
| Glucose dynamics | , () | 0.0542 (0.0478, 0.0597) | 0.0545 (0.0469, 0.0638) |
| , () | 1.4980 (1.2999, 1.6796) | 1.7023 (1.4402, 1.9112) | |
| , () | 70 (65, 75) | 80 (75, 85) | |
| , () | : −2.125 × | : 8.953 × | |
| : −2.645 × | : 6.725 × | ||
| : −2.398 × | : 5.727 × | ||
| , () | : 4.008 × | : −1.576 × | |
| : 5.055 × | : −1.025 × | ||
| : 4.426 × | : −6.536 × | ||
| , () | : −0.0112 | : 0.0057 | |
| : −0.0162 | : 0.0019 | ||
| : −0.0118 | : −0.0020 | ||
| , () | : 6.206 | : 4.813 | |
| : 8.626 | : 7.605 | ||
| : 10.75 | : 11.67 | ||
| , () | 0.1085 (0.0965, 0.1240) | 0.1085 (0.0965, 0.1240) | |
| Dynamics of the effect of insulin on glucose concentration reduction | , () | 0.1228 (0.1010, 0.1410) | 0.1224 (0.1059, 0.1408) |
| , | |||
| Insulin dynamics | , () | 0.2465 (0.2129, 0.2758) | 0.2463 (0.2154, 0.2735) |
| , | 5.63 × | 5.61 × | |
| (4.60 × , 6.33 × ) | (4.72 × , 6.56 × ) | ||
| , () | 79.03 (70.68, 122.28) [28,49] | 94.857 (76.482, 109.785) | |
| Digestion dynamics | , () | 0.0039 (−0.0333, 0.0333) | 0.0039 (−0.0333, 0.0333) |
| , (-) | 4.203 (2.755, 6.188) | 4.203 (2.755, 6.188) | |
| , () | 0.0167 (0.0144, 0.0275) | 0.0167 (0.0144, 0.0275) | |
| , () | 0.1 (−4.9140, 5.0480) | 0.1 (−4.9140, 5.0480) | |
| , () | 96.781 (20.74, 189.60) | 96.781 (20.74, 189.60) | |
| , () | 20.081 (−19.34, 115.90) | 20.081 (−19.34, 115.90) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alonso-Bastida, A.; Salazar-Piña, D.A.; Adam-Medina, M.; Gutiérrez-Xicotencatl, L.; Ríos-Enríquez, C.; Ramos-García, M.; Villanueva-Vásquez, D. A Mathematical Modeling Approach to Estimate Blood Glucose Behavior in Individuals with Prediabetes. Diabetology 2025, 6, 123. https://doi.org/10.3390/diabetology6110123
Alonso-Bastida A, Salazar-Piña DA, Adam-Medina M, Gutiérrez-Xicotencatl L, Ríos-Enríquez C, Ramos-García M, Villanueva-Vásquez D. A Mathematical Modeling Approach to Estimate Blood Glucose Behavior in Individuals with Prediabetes. Diabetology. 2025; 6(11):123. https://doi.org/10.3390/diabetology6110123
Chicago/Turabian StyleAlonso-Bastida, Alexis, Dolores Azucena Salazar-Piña, Manuel Adam-Medina, Lourdes Gutiérrez-Xicotencatl, Christian Ríos-Enríquez, Margarita Ramos-García, and Daniel Villanueva-Vásquez. 2025. "A Mathematical Modeling Approach to Estimate Blood Glucose Behavior in Individuals with Prediabetes" Diabetology 6, no. 11: 123. https://doi.org/10.3390/diabetology6110123
APA StyleAlonso-Bastida, A., Salazar-Piña, D. A., Adam-Medina, M., Gutiérrez-Xicotencatl, L., Ríos-Enríquez, C., Ramos-García, M., & Villanueva-Vásquez, D. (2025). A Mathematical Modeling Approach to Estimate Blood Glucose Behavior in Individuals with Prediabetes. Diabetology, 6(11), 123. https://doi.org/10.3390/diabetology6110123







