Spatial Distribution and Radiological Risk Assessment of Natural Radionuclides in Soils from Zacatecas, Mexico
Abstract
1. Introduction
2. Materials and Methods
2.1. Description of Study Area
2.2. Sampling and Determination of Activity Concentration
2.3. Geoaccumulation Index
2.4. Radiological Risk Assessment
2.4.1. The Radium Equivalent Activity (Raeq)
2.4.2. Absorbed Dose Rate (D)
2.4.3. Annual Effective Dose Equivalent (AEDE)
2.4.4. Radiological Risk Indices (Hex and Hin)
2.4.5. Excess Lifetime Cancer Risk (ELCR)
2.5. Statistical Methods
3. Results and Discussion
3.1. Natural Radionuclide Concentrations in Soils
3.2. Geoaccumulation Indices
3.3. Risk Assessment
3.4. Outliers
3.5. Spearman Correlation Analysis
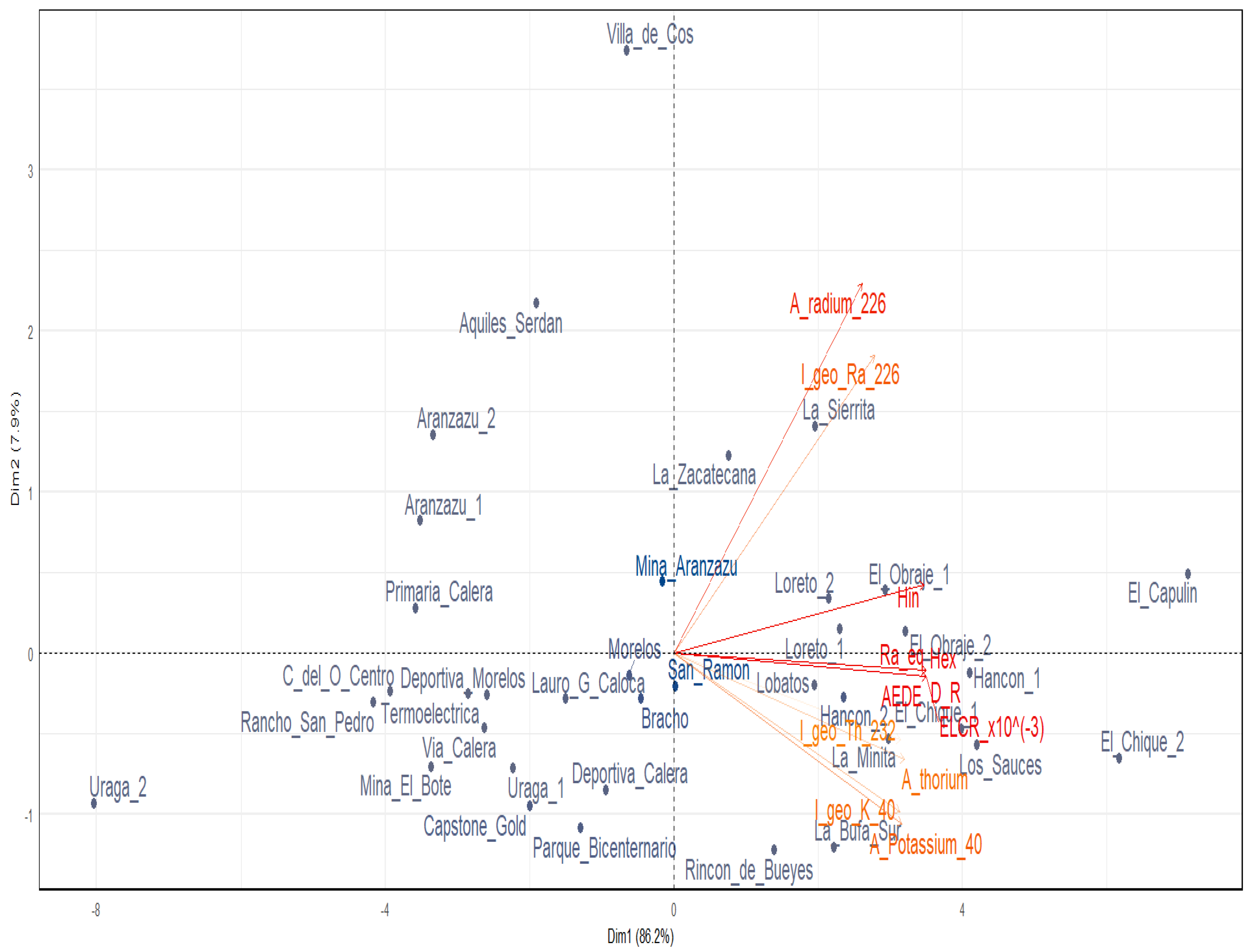
3.6. Principal Components Analysis
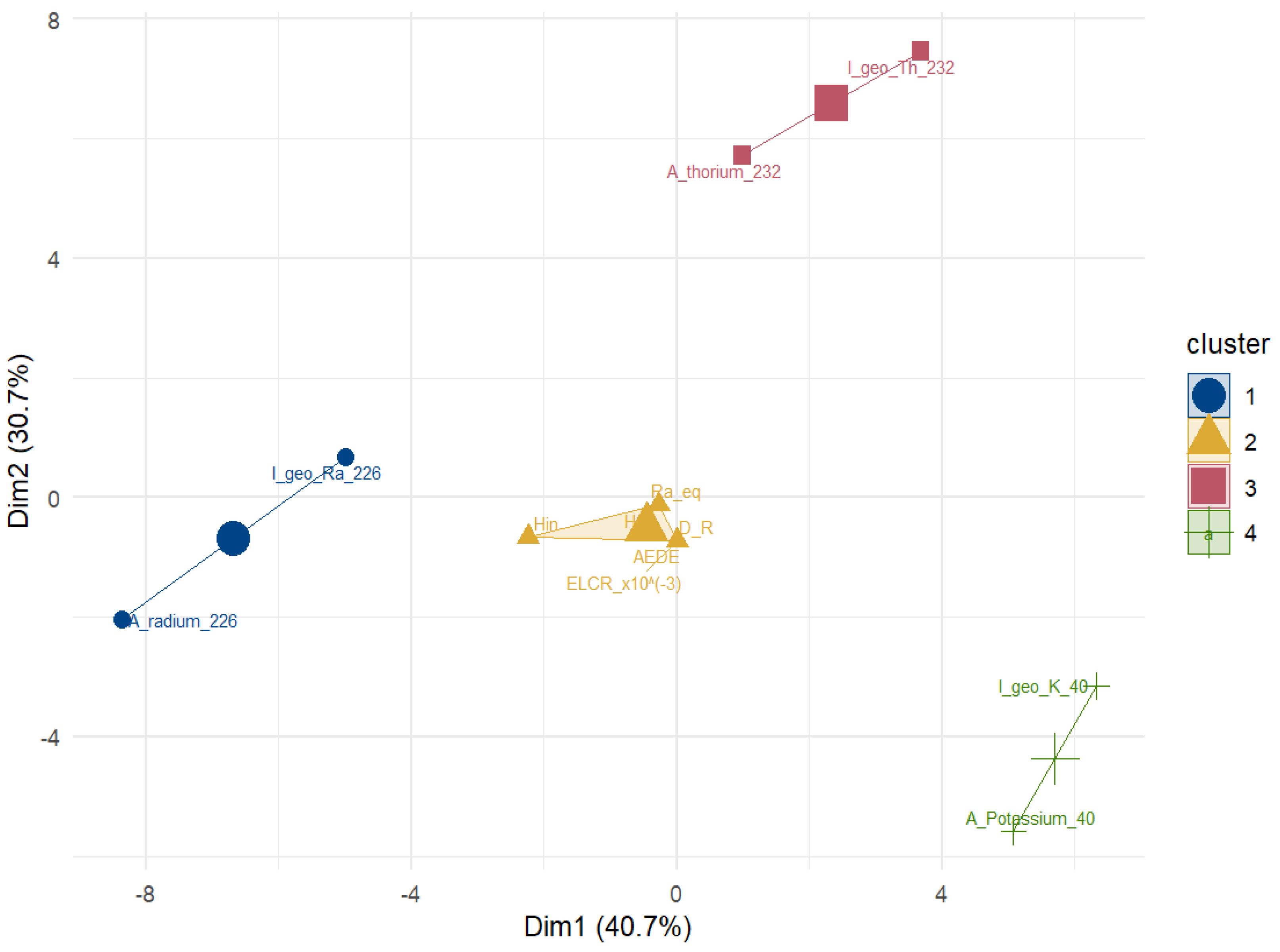
3.7. Cluster Analysis
3.7.1. Cluster Analysis in Q Mode
3.7.2. Cluster Analysis in R Mode
3.7.3. Spatial Distribution of Clusters and Hierarchical Relationships on the Map
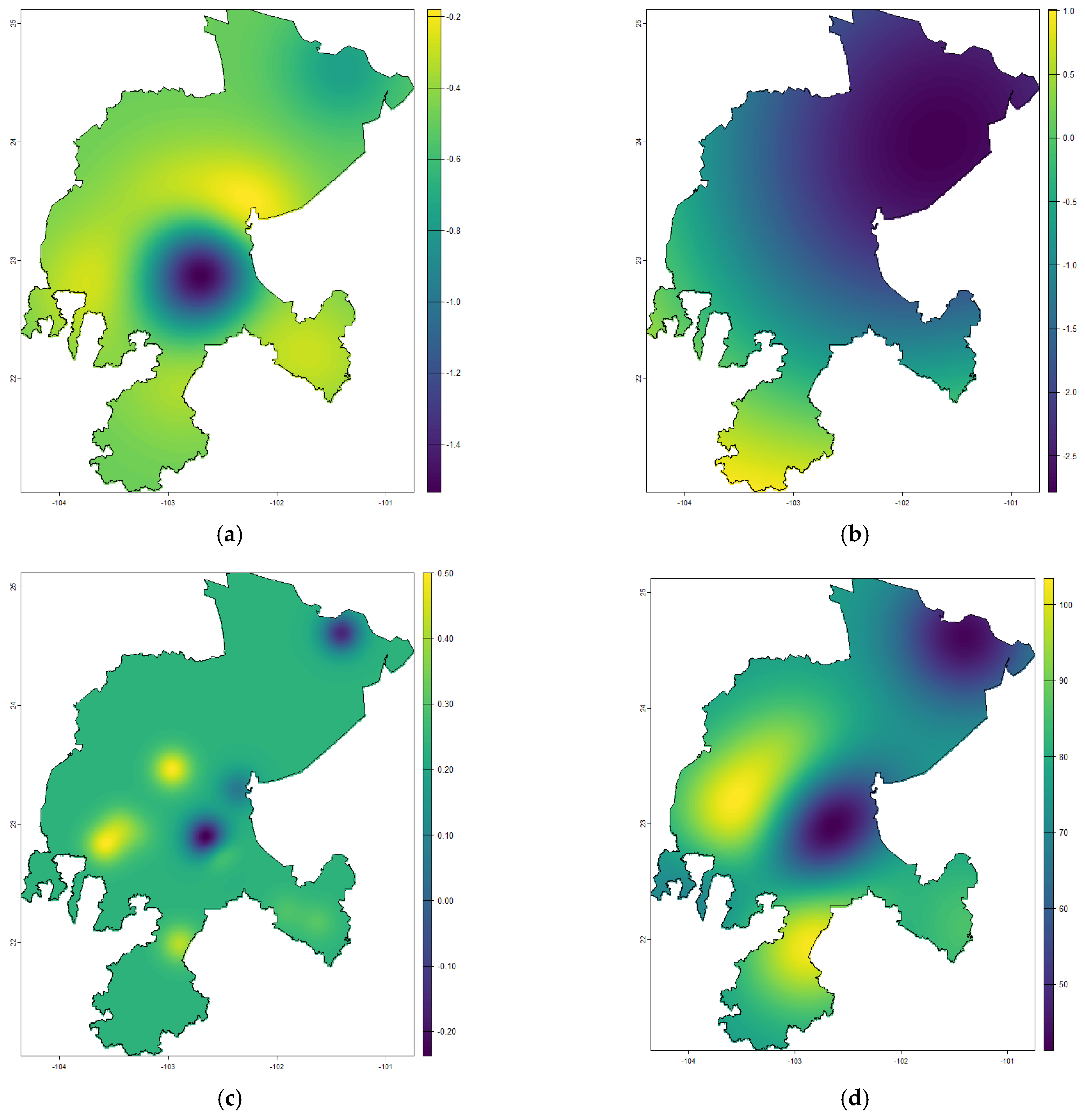
3.8. Geospatial Interpolations
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 226Ra | Radium-226 |
| 232Th | Thorium-232 |
| 40K | Potassium-40 |
| Bq | Becquerels |
| y | Year |
| kg | Kilogram |
| Gy | Gray |
| Igeo | Geoaccumulation index |
| h | Hour |
| km2 | Square kilometers |
| N | North |
| W | West |
| GeRe | Germanium reverse |
| FWHM | Full Width at Half Maximum |
| keV | kiloelectron volt |
| Eγ | Energy of the gamma rays |
| ε | Efficiency |
| γ | Gamma emission probability |
| ts | Live acquisition time |
| m | Sample mass |
| k | Correction factor |
| log2 | Logarithmic scale (base 2) |
| Ci | Measured activity concentration of the radionuclide |
| Bi | Reference background activity concentration |
| AEDE | Annual Effective Dose Equivalent |
| D | Absorbed Dose Rate |
| Raeq | Radium equivalent activity |
| Sv | Sievert |
| Hex | External hazard index |
| Hin | internal hazard index |
| ELCR | Excess Lifetime Cancer Risk |
| LE | Life expectancy |
| RF | Fatal cancer risk factor |
| AED | Annual effective dose equivalent |
| ARa | activity concentration of 226Ra |
| ATh | activity concentration of 232Th |
| AK | activity concentration of 40K |
| n | Nano |
| p | p-values |
| Correlation coefficient | |
| INEGI | Instituto Nacional de Estadística y Geografía |
Appendix A
| Samples | Site Name | Activity Concentration | Uncertainties | Samples | Site Name | Activity Concentration | Uncertainties |
|---|---|---|---|---|---|---|---|
| M1 | Bracho | 25.00 | 3.83% | M20 | Lauro G. Caloca | 20.53 | 3.88% |
| M2 | Aquiles Serdán | 43.40 | 3.70% | M21 | Lobatos | 34.04 | 3.81% |
| M3 | Concepción del oro centro (C_del_O_Centro) | 13.29 | 4.06% | M22 | Loreto 1 | 39.01 | 3.76% |
| M4 | Aranzazú 1 | 23.30 | 3.79% | M23 | Loreto 2 | 39.83 | 3.80% |
| M5 | Aranzazú 2 | 28.43 | 3.79% | M24 | Los Sauces | 38.57 | 3.84% |
| M6 | Aranzazú mine | 34.45 | 3.76% | M25 | Mina El Bote | 12.05 | 4.13% |
| M7 | Capstone Gold | 15.14 | 4.00% | M26 | Parque Bicentenario | 16.02 | 3.96% |
| M8 | Morelos | 25.28 | 4.00% | M27 | Primaria Calera | 17.26 | 3.88% |
| M9 | El Capulín | 63.98 | 3.72% | M28 | Rancho San Pedro | 11.76 | 4.12% |
| M10 | El Chique 1 | 38.08 | 3.83% | M29 | Rincón de Bueyes | 22.72 | 3.99% |
| M11 | El Chique 2 | 43.05 | 2.29% | M30 | San Ramón | 26.75 | 3.80% |
| M12 | Hancón 1 | 45.13 | 3.74% | M31 | Termoeléctrica | 16.61 | 3.89% |
| M13 | Hancón 2 | 37.16 | 3.81% | M32 | Deportiva Calera | 18.33 | 4.13% |
| M14 | El Obraje 1 | 43.19 | 3.76% | M33 | Deportiva Morelos | 17.05 | 3.97% |
| M15 | El Obraje 2 | 41.66 | 3.79% | M34 | Uraga 1 | 15.22 | 4.05% |
| M16 | La Bufa Sur | 25.43 | 3.82% | M35 | Uraga 2 | 2.05 | 9.60% |
| M17 | La Minita | 33.43 | 3.83% | M36 | Vía Calera | 15.78 | 3.96% |
| M18 | La Sierrita | 52.18 | 3.72% | M37 | Villa de Cos | 68.38 | 2.08% |
| M19 | La Zacatecana | 45.16 | 3.78% | - | - | - | - |
| Samples | Site Name | Activity Concentration | Uncertainties | Samples | Site Name | Activity Concentration | Uncertainties |
|---|---|---|---|---|---|---|---|
| M1 | Bracho | 23.68 | 3.78% | M20 | Lauro G. Caloca | 24.74 | 3.66% |
| M2 | Aquiles Serdán | 12.20 | 4.68% | M21 | Lobatos | 41.50 | 3.67% |
| M3 | Concepción del oro centro (C_del_O_Centro) | 11.16 | 4.65% | M22 | Loreto 1 | 43.01 | 3.66% |
| M4 | Aranzazú 1 | 8.48 | 5.62% | M23 | Loreto 2 | 45.79 | 3.64% |
| M5 | Aranzazú 2 | 10.10 | 4.18% | M24 | Los Sauces | 56.14 | 3.65% |
| M6 | Aranzazú mine | 14.60 | 4.08% | M25 | Mina El Bote | 12.93 | 3.89% |
| M7 | Capstone Gold | 10.65 | 3.10% | M26 | Parque Bicentenario | 16.30 | 3.90% |
| M8 | Morelos | 26.08 | 3.90% | M27 | Primaria Calera | 17.77 | 3.72% |
| M9 | El Capulín | 62.67 | 3.62% | M28 | Rancho San Pedro | 13.54 | 3.80% |
| M10 | El Chique 1 | 60.16 | 3.62% | M29 | Rincón de Bueyes | 36.16 | 3.69% |
| M11 | El Chique 2 | 83.67 | 3.60% | M30 | San Ramón | 31.18 | 3.66% |
| M12 | Hancón 1 | 40.60 | 3.65% | M31 | Termoeléctrica | 15.67 | 3.75% |
| M13 | Hancón 2 | 26.87 | 3.76% | M32 | Deportiva Calera | 23.61 | 3.74% |
| M14 | El Obraje 1 | 52.43 | 3.61% | M33 | Deportiva Morelos | 19.63 | 3.74% |
| M15 | El Obraje 2 | 53.83 | 3.61% | M34 | Uraga 1 | 18.40 | 3.84% |
| M16 | La Bufa Sur | 42.79 | 3.58% | M35 | Uraga 2 | 1.22 | 6.39% |
| M17 | La Minita | 55.82 | 3.63% | M36 | Vía Calera | 16.54 | 3.79% |
| M18 | La Sierrita | 34.61 | 3.67% | M37 | Villa de Cos | 7.95 | 2.82% |
| M19 | La Zacatecana | 27.21 | 3.66% | - | - | - | - |
| Samples | Site Name | Activity Concentration | Uncertainties | Samples | Site Name | Activity Concentration | Uncertainties |
|---|---|---|---|---|---|---|---|
| M1 | Bracho | 761.92 | 3.41% | M20 | Lauro G. Caloca | 592.95 | 3.42% |
| M2 | Aquiles Serdán | 415.17 | 3.41% | M21 | Lobatos | 880.70 | 3.41% |
| M3 | Concepción del oro centro (C_del_O_Centro) | 437.90 | 3.42% | M22 | Loreto 1 | 865.46 | 3.42% |
| M4 | Aranzazú 1 | 423.85 | 3.44% | M23 | Loreto 2 | 781.09 | 3.42% |
| M5 | Aranzazú 2 | 363.23 | 3.46% | M24 | Los Sauces | 1099.71 | 3.41% |
| M6 | Aranzazú mine | 845.16 | 3.41% | M25 | Mina El Bote | 537.74 | 3.42% |
| M7 | Capstone Gold | 811.91 | 3.41% | M26 | Parque Bicentenario | 845.24 | 3.41% |
| M8 | Morelos | 685.40 | 3.45% | M27 | Primaria Calera | 343.91 | 3.44% |
| M9 | El Capulín | 1320.07 | 3.40% | M28 | Rancho San Pedro | 380.82 | 3.44% |
| M10 | El Chique 1 | 999.93 | 3.41% | M29 | Rincón de Bueyes | 1005.78 | 3.41% |
| M11 | El Chique 2 | 1079.68 | 3.41% | M30 | San Ramón | 722.50 | 3.41% |
| M12 | Hancón 1 | 1222.91 | 3.40% | M31 | Termoeléctrica | 521.38 | 3.42% |
| M13 | Hancón 2 | 1157.62 | 3.40% | M32 | Deportiva Calera | 760.74 | 3.44% |
| M14 | El Obraje 1 | 808.84 | 3.41% | M33 | Deportiva Morelos | 503.25 | 3.43% |
| M15 | El Obraje 2 | 870.47 | 3.41% | M34 | Uraga 1 | 624.01 | 3.42% |
| M16 | La Bufa Sur | 1048.21 | 3.40% | M35 | Uraga 2 | 202.63 | 3.49% |
| M17 | La Minita | 904.41 | 3.41% | M36 | Vía Calera | 563.43 | 3.42% |
| M18 | La Sierrita | 741.02 | 3.41% | M37 | Villa de Cos | 444.16 | 1.72% |
| M19 | La Zacatecana | 688.94 | 3.40% | - | - | - | - |
References
- Cinelli, G.; Tollefsen, T.; Bossew, P.; Gruber, V.; Bogucarskis, K.; De Felice, L.; De Cort, M. Digital version of the European Atlas of natural radiation. J. Environ. Radioact. 2019, 196, 240–252. [Google Scholar] [CrossRef] [PubMed]
- Isinkaye, M.O.; Emelue, H.U. Natural radioactivity measurements and evaluation of radiological hazards in sediment of Oguta Lake, South East Nigeria. J. Radiat. Res. Appl. Sci. 2015, 8, 459–469. [Google Scholar] [CrossRef]
- Mbonu, C.C.; Ben, U.C. Assessment of radiation hazard indices due to natural radioactivity in soil samples from Orlu, Imo State, Nigeria. Heliyon 2021, 7, e07812. [Google Scholar] [CrossRef]
- Chandra, K.; Proshad, R.; Dey, H.C.; Idris, A.M. A review on radionuclide pollution in global soils with environmental and health hazards evaluation. Environ. Geochem. Health 2023, 45, 9245–9266. [Google Scholar] [CrossRef]
- Beretka, J.; Mathew, P.J. Natural Radioactivity of Australian Building Materials, Industrial Wastes and By-products. Health Phys. 1985, 48, 87–95. [Google Scholar] [CrossRef]
- Bajoga, A.D.; Alazemi, N.; Shams, H.; Regan, P.H.; Bradley, D.A. Evaluation of naturally occurring radioactivity across the State of Kuwait using high-resolution gamma-ray spectrometry. Radiat. Phys. Chem. 2017, 137, 203–209. [Google Scholar] [CrossRef]
- Bajoga, A.D.; Al-Dabbous, A.N.; Abdullahi, A.S.; Alazemi, N.A.; Bachama, Y.D.; Alaswad, S.O. Evaluation of elemental concentrations of uranium, thorium and potassium in top soils from Kuwait. Nucl. Eng. Technol. 2019, 51, 1638–1649. [Google Scholar] [CrossRef]
- Krishnamoorthi, T.; Bramha, S.; Chandrasekaran, S.; Ravichandaran, R.; Sivakumar, S.; Ravisankar, R. Measurement of natural radioactivity and assessment of radiological hazard indices in soil from Tirunelveli District, Tamil Nadu, India with statistical approach. Nucl. Anal. 2025, 4, 100156. [Google Scholar] [CrossRef]
- Mubarak, F.; Fayez-Hassan, M.; Mansour, N.A.; Ahmed, T.S.; Ali, A. Radiological Investigation of High Background Radiation Areas. Sci. Rep. 2017, 7, 15223. [Google Scholar] [CrossRef]
- Yasmin, S.; Barua, B.S.; Khandaker, M.U.; Kamal, M.; Rashid, A.; Sani, S.A.; Ahmed, H.; Nikouravan, B.; Bradley, D. The presence of radioactive materials in soil, sand and sediment samples of Potenga sea beach area, Chittagong, Bangladesh: Geological characteristics and environmental implication. Results Phys. 2018, 8, 1268–1274. [Google Scholar] [CrossRef]
- Feng, W.; Zhang, Y.; Li, Y.; Wang, P.; Zhu, C.; Shi, L.; Hou, X.; Qie, X. Spatial distribution, risk assessment and influence factors of terrestrial gamma radiation dose in China. J. Environ. Radioact. 2020, 222, 106325. [Google Scholar] [CrossRef] [PubMed]
- Altıkulaç, A.; Turhan, Ş.; Gümüş, H. Activity concentration of terrestrial and anthropogenic radionuclides (226Ra, 222Rn, 232Th, 40K, and 137Cs) in soil samples. Environ. Earth Sci. 2016, 75, 41. [Google Scholar] [CrossRef]
- Escareño-Juárez, E.; Pardo, R.; Gascó-Leonarte, C.; Vega, M.; Sánchez-Báscones, M.I.; Barrado-Olmedo, A.I. Determination of natural uranium by various analytical techniques in soils of Zacatecas State (Mexico). J. Radioanal. Nucl. Chem. 2019, 319, 1135–1144. [Google Scholar] [CrossRef]
- Escareño-Juarez, E.; Jiménez-Barredo, F.; Gascó-Leonarte, C.; Barrado-Olmedo, A.I.; Vega, M. Baseline thorium concentration and isotope ratios in topsoil of Zacatecas State, Mexico. Chemosphere 2021, 268, 128915. [Google Scholar] [CrossRef]
- Ibraheem, A.A.; El-Taher, A.; Alruwaili, M.H.M. Assessment of natural radioactivity levels and radiation hazard indices for soil samples from Abha, Saudi Arabia. Results Phys. 2018, 11, 325–330. [Google Scholar] [CrossRef]
- Olarinoye, I.O.; Kolo, M.T.; Shittu, H.O.; Anumah, A.S. Estimation of indoor gamma radiation dose rate from concrete blocks constructed from tin mine tailings. J. Build. Eng. 2023, 66, 105934. [Google Scholar] [CrossRef]
- La Verde, G.; Raulo, A.; D’Avino, V.; Roca, V.; Pugliese, M. Radioactivity content in natural stones used as building materials in Puglia region analysed by high resolution gamma-ray spectroscopy: Preliminary results. Constr. Build. Mater. 2020, 239, 117668. [Google Scholar] [CrossRef]
- Guastaldi, E.; Baldoncini, M.; Bezzon, G.; Broggini, C.; Buso, G.; Caciolli, A.; Carmignani, L.; Callegari, I.; Colonna, T.; Dule, K.; et al. A multivariate spatial interpolation of airborne γ-ray data using the geological constraints. Remote Sens. Environ. 2013, 137, 1–11. [Google Scholar] [CrossRef]
- Kurnaz, A.; Kucukomeroglu, B.; Damla, N.; Cevik, U. Radiological maps for Trabzon, Turkey. J. Environ. Radioact. 2011, 102, 393–399. [Google Scholar] [CrossRef]
- Santhanabharathi, B.; Ahmed, M.S.; Chandrasekaran, A.; Priyadharshini, M.; Pradhoshini, K.P.; Aarthi, M.; Sathish, V.; Krishnamoorthy, R.; Duong, V.-H.; Rahman, I.M.; et al. Spatial distribution and radiological risk assessment of natural radionuclides in sediments from Kayamkulam Estuary, Kerala. Environ. Pollut. Manag. 2025, 2, 77–86. [Google Scholar] [CrossRef]
- Kaintura, S.S.; Devi, S.; Tiwari, K.; Thakur, S.; Sebastian, R.; Singh, P.P. Gamma-spectroscopic assessment of radionuclides and radiological hazards in undisturbed and cultivated soils of Rupnagar, Punjab, India. Nucl. Eng. Technol. 2025, 57, 103418. [Google Scholar] [CrossRef]
- Aközcan, S.; Külahcı, F.; Mercan, Y. A suggestion to radiological hazards characterization of 226Ra, 232Th, 40K and 137Cs: Spatial distribution modelling. J. Hazard. Mater. 2018, 353, 476–489. [Google Scholar] [CrossRef] [PubMed]
- Ogundele, L.T.; Ayeku, P.O.; Inuyomi, S.O.; Ogunsakin, O.M.; Oladejo, O.F.; Adejoro, I.A. Assessment of naturally occurring 40K, 232Th and 238U and their associated radiological hazard indices in soils used for building in Ondo West Local Government Area, Southwestern, Nigeria. EQA Int. J. Environ. Qual. 2020, 37, 11–21. [Google Scholar] [CrossRef]
- Reddy, G.S.; Reddy, K.V.K.; Reddy, B.S.; Reddy, M.S.; Reddy, C.G.; Reddy, P.Y. Mapping of ambient gamma radiation levels and risk assessment in some parts of Eastern Deccan Plateau, India. Int. J. Environ. Anal. Chem. 2023, 103, 5355–5367. [Google Scholar] [CrossRef]
- Narayana, Y.; Rajashekara, K.M. The importance of physico-chemical parameters on the speciation of natural radionuclides in riverine ecosystems. J. Environ. Radioact. 2010, 101, 958–964. [Google Scholar] [CrossRef]
- Wikipedia. Zacatecas. Available online: https://en.wikipedia.org/wiki/Zacatecas (accessed on 21 January 2025).
- Wikipedia. Zacatecas. Available online: https://en.wikipedia.org/wiki/Zacatecas_(city) (accessed on 5 March 2025).
- Bautista-Capetillo, C. Agroclimatic Zoning of Semiarid Region of Zacatecas, Mexico. Appl. Ecol. Environ. Res. 2018, 16, 251–266. [Google Scholar] [CrossRef]
- Instituto Nacional de Estadística y Geografía. Conociendo Zacatecas; Instituto Nacional de Estadística y Geografía: Aguascalientes, Mexico, 2013; Available online: https://en.www.inegi.org.mx (accessed on 4 April 2025).
- Instituto Nacional de Estadística y Geografía. Aspectos Geográficos de Zacatecas; Instituto Nacional de Estadística y Geografía: Aguascalientes, Mexico, 2021. [Google Scholar]
- Instituto Nacional de Estadística y Geografía. Aspectos Geográficos de Zacatecas, Compendio 2022; Instituto Nacional de Estadística y Geografía: Aguascalientes, Mexico, 2023; Available online: https://www.inegi.org.mx/ (accessed on 4 April 2025).
- Iaea. Guidelines for Radioelement Mapping Using Gamma Ray Spectrometry Data; IAEA-TECDOC-1363; Iaea: Vienna, Austria, 2003. [Google Scholar]
- ISO 18589-1:2005; Measurement of Radioactivity in the Environment—Soil Part 1: General Guidelines and Definitions. British Standards Institution (BSI): London, UK, 2008.
- Gilmore, G. Practica Gamma-Ray Spectrometry, 2nd ed.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2008. [Google Scholar]
- Cember, H.; Johnson, T.E. Introduction to Health Physics, 4th ed.; McGraw Hill Companies, Inc.: New York, NY, USA, 2008. [Google Scholar]
- Magil, J.; Galy, J. Radioactivity, Radionuclides, Radiation; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Canberra Industries. Genie-2000 Spectroscopy Software Operations, Edition 3.2.1. ed; Canberra Industries: Meriden, CT, USA, 2009. [Google Scholar]
- Done, L.; Ioan, M.-R. Minimum Detectable Activity in gamma spectrometry and its use in low level activity measurements. Appl. Radiat. Isot. 2016, 114, 28–32. [Google Scholar] [CrossRef]
- Pamela, D.G.; Anna, B. Semi-Annual Report of the Department of Energy, Office of Environmental Management, Quality Assessment Program; Department of Energy: New York, NY, USA, 2001. [Google Scholar]
- Ramírez, D.H.; Martínez, C.R.; Vega, J.L.P.; Espinosa, A.Z.L.; Mauricio, V.H. Calibración semi-empírica de un detector de germanio hiperpuro para mediciones in situ de radionúclidos naturales. Investig. Científica 2020, 14, 53–61. [Google Scholar]
- Al-Masri, M.S.; Doubal, A.W. Validation of in situ and laboratory gamma spectrometry measurements for determination of 226Ra, 40K and 137Cs in soil. Appl. Radiat. Isot. 2013, 75, 50–57. [Google Scholar] [CrossRef]
- Muller, G. Index of geoaccumulation in sediments of the Rhine river. Geol. J. 1969, 2, 108–118. [Google Scholar]
- Wang, L.; Dai, L.; Li, L.; Liang, T. Multivariable cokriging prediction and source analysis of potentially toxic elements (Cr, Cu, Cd, Pb, and Zn) in surface sediments from Dongting Lake, China. Ecol. Indic. 2018, 94, 312–319. [Google Scholar] [CrossRef]
- UNSCEAR. Sources and Effects of Ionising Radiation; United Nations Publications: New York, NY, USA, 2000; Volume 1. [Google Scholar]
- Ion, A.; Cosac, A.; Ene, V.V. Natural Radioactivity in Soil and Radiological Risk Assessment in Lișava Uranium Mining Sector, Banat Mountains, Romania. Appl. Sci. 2022, 12, 12363. [Google Scholar] [CrossRef]
- Boukhalfa, S.; Khelifi, R. Gamma-ray Spectrometry and X-ray Fluorescence Analysis for Natural Radioactivity Evaluation Associated with Radiation Hazard in Construction Materials. Jordan J. Phys. 2023, 16, 207–214. [Google Scholar] [CrossRef]
- Tufail, M.; Nasim-Akhtar; Sabiha-Javied; Hamid, T. Natural radioactivity hazards of building bricks fabricated from saline soil of two districts of Pakistan. J. Radiol. Prot. 2007, 27, 481–492. [Google Scholar] [CrossRef]
- Tufail, M. Radium equivalent activity in the light of UNSCEAR report. Environ. Monit. Assess. 2012, 184, 5663–5667. [Google Scholar] [CrossRef]
- Hamilton, E.I. The Relative Radioactivity of Building Materials. Am. Ind. Hyg. Assoc. J. 1971, 32, 398–403. [Google Scholar] [CrossRef]
- United Nations Scientific Committee on the Effects of Atomic Radiation. Sources and Effects of Ionizing Radiation. UNSCEAR 2008 Report to the General Assembly; United Nations Scientific Committee on the Effects of Atomic Radiation: Vienna, Austria, 2008. [Google Scholar]
- Instituto Nacional de Estadística y Geografía. Esperanza de Vida al Nacimiento Por Entidad Federativa Según Sexo, Serie Anual de 2010 a 2024; INEGI: Aguascalientes, México, 2024. [Google Scholar]
- ICRP. The 2007 Recommendations of the International Commission on Radiological Protection; Ann ICRP: London, UK, 2007; Volume ICRP-103. [Google Scholar]
- Team, R.C. R: A Language and Environment for Statistical Computing, Edition 4.4.2. ed; R Foundation for Statistical Computing: Vienna, Austria, 2024; Available online: https://www.R-project.org/ (accessed on 21 January 2025).
- Komsta, L.; Novomestky, F. Moments: Moments, Cumulants, Skewness, Kurtosis and Related Tests, 2022; 0.14.1. Available online: https://CRAN.R-project.org/package=moments (accessed on 21 January 2025).
- Wei, T.; Simko, V. R package ‘corrplot’: Visualization of a Correlation Matrix, 2024; 0.95. Available online: https://github.com/taiyun/corrplot (accessed on 21 January 2025).
- Siegel, S.; Castellan, N.J. Estadística no Paramétrica Aplicada a las Ciencias de la Conducta, 4th ed.; Trillas: Miami Lakes, FL, USA, 1995. [Google Scholar]
- Xu, R.; Wunsch, I.D.C. Clustering; John Wiley & Sons, Inc: New York, NY, USA, 2009. [Google Scholar]
- Li, X.; Feng, L. Multivariate and geostatistical analyzes of metals in urban soil of Weinan industrial areas, Northwest of China. Atmos. Environ. 2012, 47, 58–65. [Google Scholar] [CrossRef]
- Maechler, M.; Rousseeuw, P.; Struyf, A.; Hubert, M.; Hornik, K. Cluster: Cluster Analysis Basics and Extensions, 2023; 2.1.6. Available online: https://CRAN.R-project.org/package=cluster (accessed on 21 January 2025).
- Galili, T. Dendextend: An R package for visualizing, adjusting and comparing trees of hierarchical clustering. Bioinformatics 2015, 31, 3718–3720. [Google Scholar] [CrossRef]
- Kassambara, A. Multivariate Analysis II: Practical Guide to Principal Component Methods in R, 1st ed.; STHDA: Stanford, CA, USA, 2017; Volume II. [Google Scholar]
- Palacio, F.X.; Apodaca, M.J.; Crisci, J.V. Análisis Multivariado para Datos Biológicos: Teoría y sus Aplicaciones Utilizando el Lenguaje R, 1st ed.; Fundación de Historia Natural Félix de Azara: Buenos Aires, Argentina, 2020. [Google Scholar]
- Malinowski, E.R. Factor Analysis in Chemistry, 3rd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2002. [Google Scholar]
- Kassambara, A.; Mundt, F. Factoextra: Extract and Visualize the Results of Multivariate Data Analyses, 2020; 1.0.7. Available online: https://CRAN.R-project.org/package=factoextra (accessed on 21 January 2025).
- Benedikt, G.; Pebesma, E.; Heuvelink, G. Spatio-Temporal Interpolation using gstat. R. J. 2016, 8, 204–218. [Google Scholar]
- Pebesma, E.J. Multivariable geostatistics in S: The gstat package. Comput. Geosci. 2004, 30, 683–691. [Google Scholar] [CrossRef]
- Hijmans, R.J. Terra: Spatial Data Analysis, 2024; 1.7-83. Available online: https://CRAN.R-project.org/package=terra (accessed on 21 January 2025).
- Li, J.; Heap, A.D. A review of comparative studies of spatial interpolation methods in environmental sciences: Performance and impact factors. Ecol. Inform. 2011, 6, 228–241. [Google Scholar] [CrossRef]
- Yeşilkanat, C.M.; Kobya, Y.; Taşkin, H.; Çevik, U. Dose rate estimates and spatial interpolation maps of outdoor gamma dose rate with geostatistical methods; A case study from Artvin, Turkey. J. Environ. Radioact. 2015, 150, 132–144. [Google Scholar] [CrossRef] [PubMed]
- Moraga, P. Spatial Statistics for Data Science: Theory and Practice with R, 1st ed.; Data Science Series; Chapman & Hall/CRC Data: New York, NY, USA, 2023. [Google Scholar]
- Moraga, P. Geospatial Health Data: Modeling and Visualization with R-INLA and Shiny; Biostatistics Series; Chapman & Hall/CRC: New York, NY, USA, 2019. [Google Scholar]
- Venables, W.N.; Ripley, B.D. Modern Applied Statistics with S, 4th ed.; Springer: New York, NY, USA, 2002; Available online: https://www.stats.ox.ac.uk/pub/MASS4/ (accessed on 5 March 2025).
- Bivand, R. R Packages for Analyzing Spatial Data: A Comparative Case Study with Areal Data. Geogr. Anal. 2022, 54, 488–518. [Google Scholar] [CrossRef]
- Bivand, R.S.; Wong, D.W.S. Comparing implementations of global and local indicators of spatial association. Test 2018, 27, 716–748. [Google Scholar] [CrossRef]
- Pebesma, E.; Bivand, R. Spatial Data Science; Chapman and Hall/CRC: New York, NY, USA, 2023. [Google Scholar] [CrossRef]
- Bivand, R.S.; Pebesma, E.; Gómez-Rubio, V. Applied Spatial Data Analysis with R; Springer: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Series in Statistics; Springer: New York, NY, USA, 2009; Available online: https://books.google.com.mx/books?id=eBSgoAEACAAJ (accessed on 17 February 2024).
- Balzarini, M.; Bruno, C.; Córdoba, M.; Teich, I. Herramientas en el Análisis Estadístico Multivariado; Editorial Universidad del Norte: Barranquilla, Colombia, 2015. [Google Scholar]
- Chávez, A.G. 100 Problemas Resueltos de Estadística Multivariante Implementados en Matlab; Delta Publicaciones: Kiel, WI, USA, 2007; Available online: https://books.google.com.mx/books?id=mejciP3IAygC (accessed on 14 October 2023).
- Mardia, K.V.; Kent, J.T.; Kent, J.T.; Bibby, J.M. Multivariate Analysis in Probability and Mathematical Statistics: A Series of Monographs and Textbooks; Academic Press: New York, NY, USA, 1979. [Google Scholar]
- Härdle, W.K.; Simar, L. Applied Multivariate Statistical Analysis; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Johnson, R.A.; Wichern, D.W. Applied Multivariate Statistical Analysis, 6th ed.; PearsonPrentice Hall: Upper Saddle River, NJ, USA, 2007. [Google Scholar]
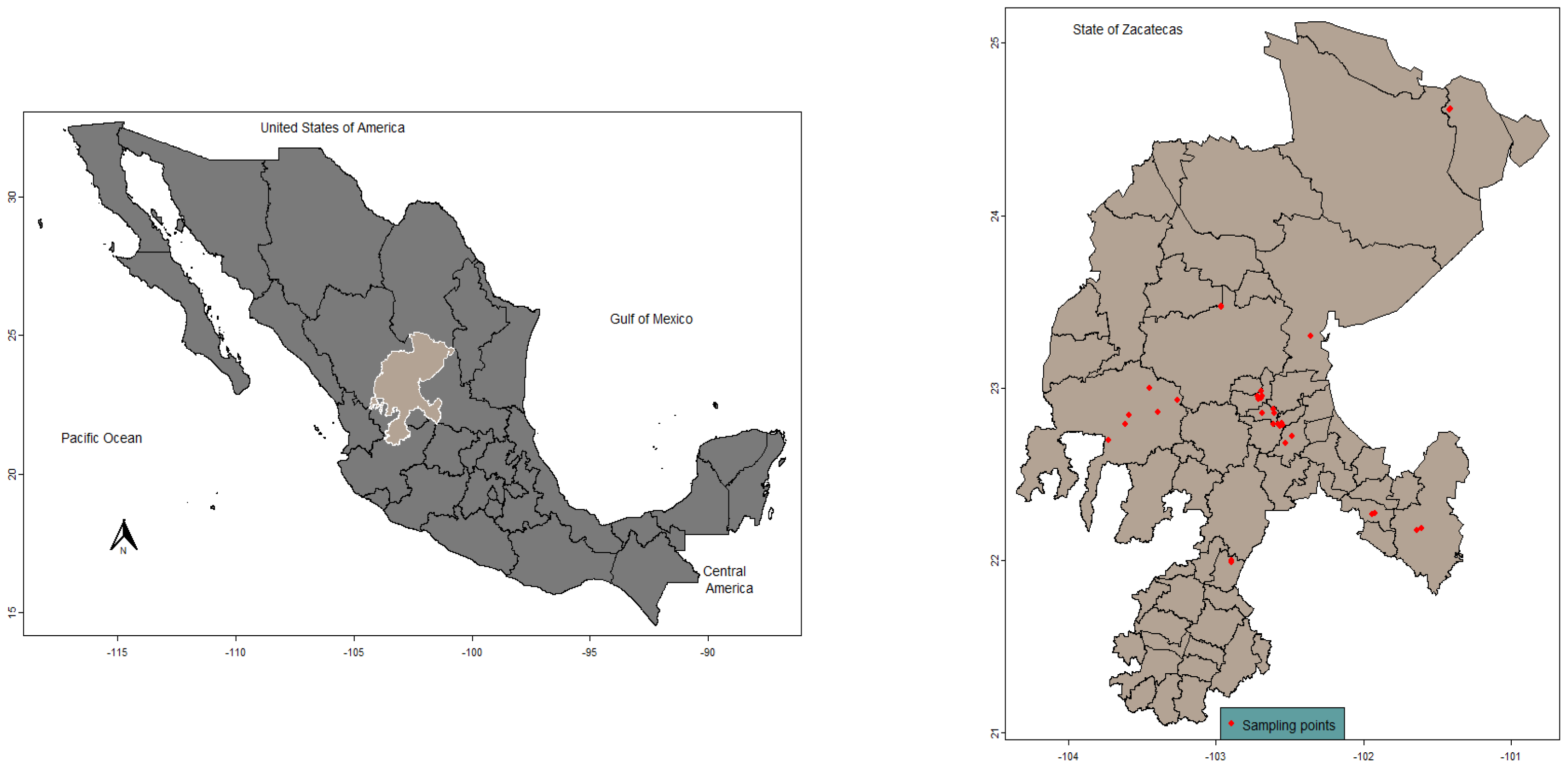
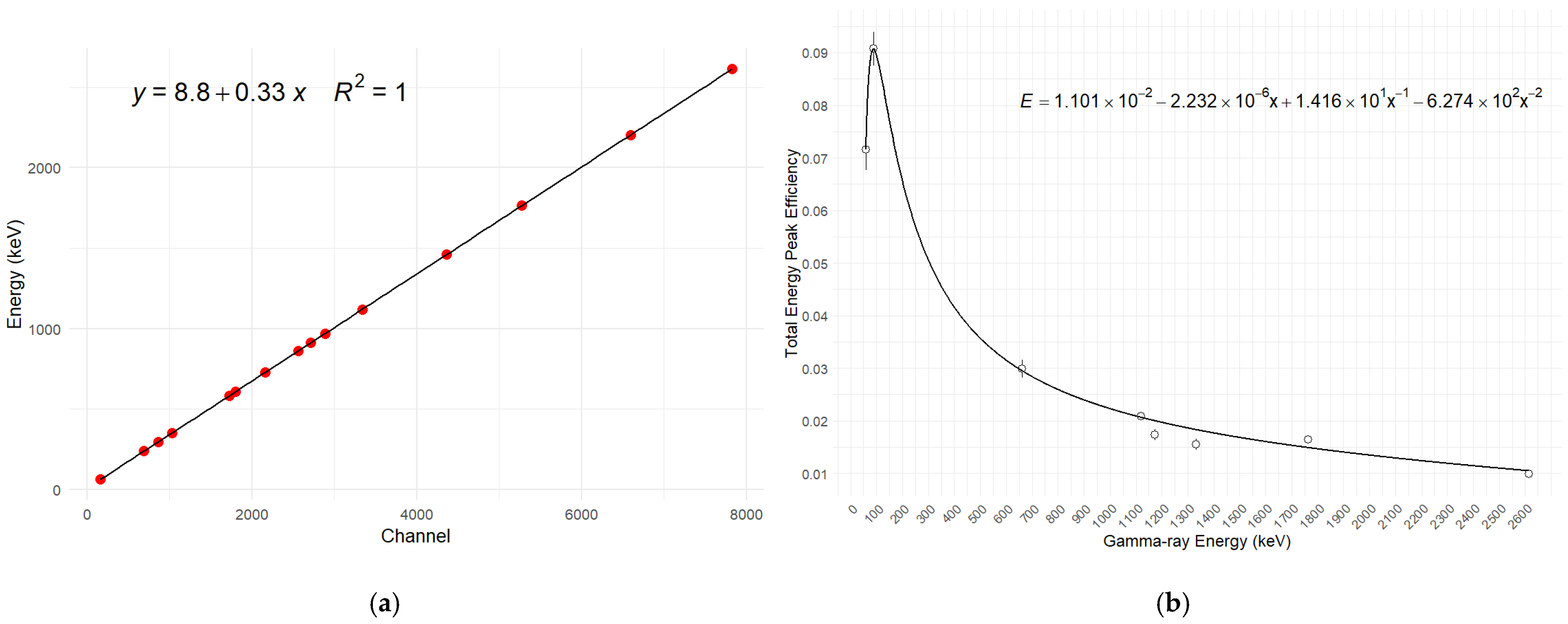
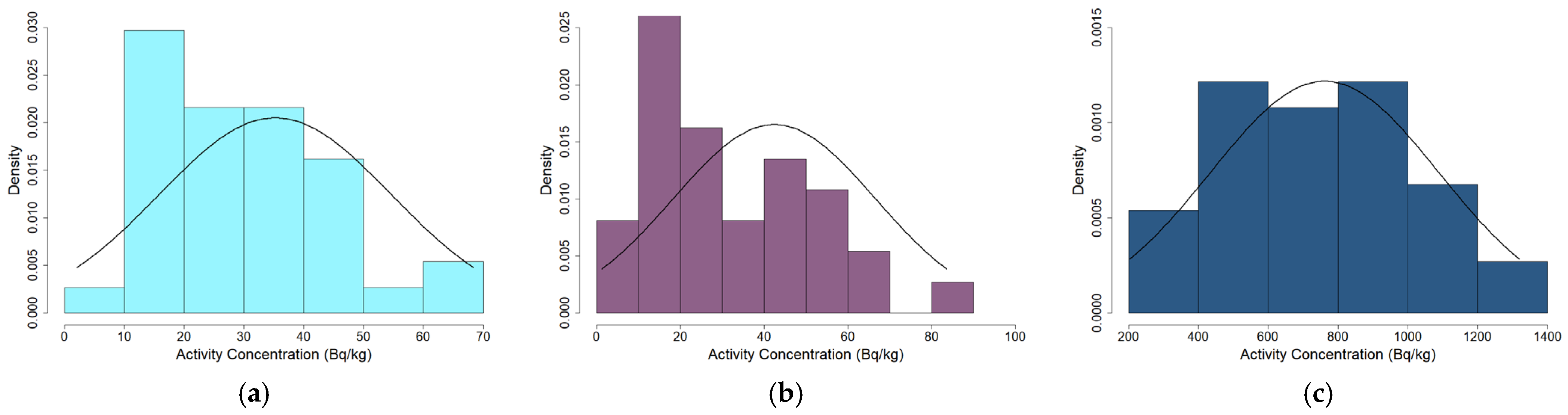
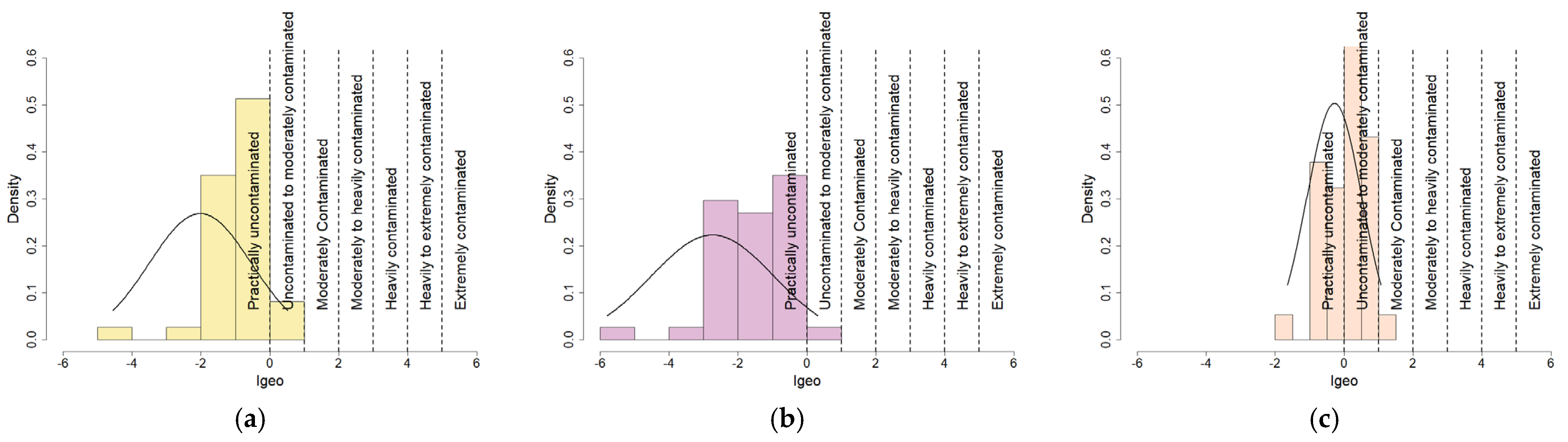



| Samples | Site Name | Latitude | Longitude | Samples | Site Name | Latitude | Longitude |
|---|---|---|---|---|---|---|---|
| M1 | Bracho | 22.7933 | −102.5553 | M20 | Lauro G. Caloca | 22.9514 | −102.7152 |
| M2 | Aquiles Serdán | 24.6142 | −101.4141 | M21 | Lobatos | 22.858 | −103.3933 |
| M3 | Concepción del oro centro (C_del_O_Centro) | 24.6213 | −101.4086 | M22 | Loreto 1 | 22.2705 | −101.9213 |
| M4 | Aranzazú 1 | 24.6213 | −101.4075 | M23 | Loreto 2 | 22.2693 | −101.9381 |
| M5 | Aranzazú 2 | 24.6212 | −101.4126 | M24 | Los Sauces | 23.0016 | −103.4475 |
| M6 | Aranzazú mine | 24.6206 | −101.4109 | M25 | Mina El Bote | 22.7876 | −102.61 |
| M7 | Capstone Gold | 22.7909 | −102.5794 | M26 | Parque Bicentenario | 22.7814 | −102.5449 |
| M8 | Morelos | 22.8563 | −102.6044 | M27 | Primaria Calera | 22.9435 | −102.6942 |
| M9 | El Capulín | 22.8408 | −103.5888 | M28 | Rancho San Pedro | 22.8554 | −102.6879 |
| M10 | El Chique 1 | 21.9986 | −102.8953 | M29 | Rincón de Bueyes | 22.792 | −103.613 |
| M11 | El Chique 2 | 21.9885 | −102.8917 | M30 | San Ramón | 22.6765 | −102.525 |
| M12 | Hancón 1 | 23.4695 | −102.9652 | M31 | Termoeléctrica | 22.9832 | −102.6947 |
| M13 | Hancón 2 | 23.475 | −102.9644 | M32 | Deportiva Calera | 22.9365 | −102.7081 |
| M14 | El Obraje 1 | 22.1842 | −101.6065 | M33 | Deportiva Morelos | 22.8543 | −102.6069 |
| M15 | El Obraje 2 | 22.1747 | −101.635 | M34 | Uraga 1 | 22.8745 | −102.6083 |
| M16 | La Bufa Sur | 22.7768 | −102.5644 | M35 | Uraga 2 | 22.874 | −102.6088 |
| M17 | La Minita | 22.93 | −103.2625 | M36 | Vía Calera | 22.9523 | −102.6844 |
| M18 | La Sierrita | 22.6958 | −103.7291 | M37 | Villa de Cos | 23.3026 | −102.3592 |
| M19 | La Zacatecana | 22.7224 | −102.4865 | - | - | - | - |
| Eigenvalue | Variance Percent | Cumulative Variance Percent | Variables | Correlation (p Value) | |
|---|---|---|---|---|---|
| Dim. 1 | 10.03 | 86.21 | 86.21 | D (Absorbed dose rate) | 0.9956 (1.11 × 10−37) |
| AEDE (Annual effective dose equivalent) | 0.9956 (1.11 × 10−37) | ||||
| ELCR × 10−3 (Excess lifetime cancer risk) | 0.9956 (1.11 × 10−37) | ||||
| Hex (External hazard index) | 0.9948 (2.06 × 10−36) | ||||
| Raeq (radium equivalent activity) | 0.9948 (2.10 × 10−36) | ||||
| Hin (Internal hazard index) | 0.9876 (9.59 × 10−30) | ||||
| A_thorium_232 (activity concentration 232Th) | 0.9098 (9.59 × 10−30) | ||||
| A_Potassium_40 (activity concentration 40K) | 0.9002 (3.39 × 10−14) | ||||
| I_geo_Th_232 (Igeo 232Th) | 0.8950 (7.93 × 10−14) | ||||
| I_geo_K_40 (Igeo 40K) | 0.8920 (1.26 × 10−13) | ||||
| I_geo_Ra_226 (Igeo 226Ra) | 0.7929 (4.88 × 10−9) | ||||
| A_radium_226 (activity concentration 226Ra) | 0.7433 (1.36 × 10−7) | ||||
| Dim. 2 | 0.95 | 7.94 | 94.15 | A_radium_226 (activity concentration 226Ra) | 0.6521 (1.22 × 10−5) |
| I_geo_Ra_226 (Igeo 226Ra) | 0.5260 (8.25 × 10−4) | ||||
| Dim. 3 | 0.37 | 3.12 | 97.28 | I_geo_K_40 (Igeo 40K) | 0.3404 (0.039) |
| A_thorium_232 (activity concentration 232Th) | −0.3641 (0.027) |
| Variable | RMSE | MAE | Pseudo R2 | Model | Nugget | Sill | Kappa | Range (m) |
|---|---|---|---|---|---|---|---|---|
| Igeo226Ra | 0.754 | 0.458 | 0.316 | Ste | 0.734 | 1.223 | 10 | 57,420.02 |
| Igeo 232Th | 0.908 | 0.600 | 0.372 | Ste | 1.085 | 7.323 | 10 | 359,346.8 |
| Igeo 40K | 0.494 | 0.387 | 0.307 | Ste | 0.269 | 0.352 | 10 | 18,033.37 |
| Raeq(Bqkg−1) | 31.429 | 24.014 | 0.668 | Gau | 889.301 | 5328.633 | - | 71,039.08 |
| D(nGyh−1) | 14.900 | 11.202 | 0.663 | Gau | 204.338 | 1118.800 | - | 65,635.04 |
| AEDE(μSvy−1) | 18.273 | 13.740 | 0.663 | Gau | 307.335 | 1682.739 | - | 65,635.04 |
| Hex | 0.085 | 0.065 | 0.668 | Gau | 0.006 | 0.330 | - | 71,036.06 |
| Hin | 0.108 | 0.084 | 0.636 | Gau | 0.010 | 0.059 | - | 68,692.92 |
| ELCR × 10−3 | 0.079 | 0.059 | 0.663 | Gau | 0.006 | 0.031 | - | 65,635.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hernández-Ramírez, D.; Ríos-Martínez, C.; Pinedo-Vega, J.L.; Mireles-García, F.; De la Torre Aguilar, F.; Escareño-Juárez, E. Spatial Distribution and Radiological Risk Assessment of Natural Radionuclides in Soils from Zacatecas, Mexico. Analytica 2025, 6, 20. https://doi.org/10.3390/analytica6020020
Hernández-Ramírez D, Ríos-Martínez C, Pinedo-Vega JL, Mireles-García F, De la Torre Aguilar F, Escareño-Juárez E. Spatial Distribution and Radiological Risk Assessment of Natural Radionuclides in Soils from Zacatecas, Mexico. Analytica. 2025; 6(2):20. https://doi.org/10.3390/analytica6020020
Chicago/Turabian StyleHernández-Ramírez, Daniel, Carlos Ríos-Martínez, José Luis Pinedo-Vega, Fernando Mireles-García, Fernando De la Torre Aguilar, and Edmundo Escareño-Juárez. 2025. "Spatial Distribution and Radiological Risk Assessment of Natural Radionuclides in Soils from Zacatecas, Mexico" Analytica 6, no. 2: 20. https://doi.org/10.3390/analytica6020020
APA StyleHernández-Ramírez, D., Ríos-Martínez, C., Pinedo-Vega, J. L., Mireles-García, F., De la Torre Aguilar, F., & Escareño-Juárez, E. (2025). Spatial Distribution and Radiological Risk Assessment of Natural Radionuclides in Soils from Zacatecas, Mexico. Analytica, 6(2), 20. https://doi.org/10.3390/analytica6020020









