Quantification of Recycled PET in Commercial Bottles by IR Spectroscopy and Chemometrics

Abstract

A novel approach for the quantification of recycled polyethylene terephthalate (r-PET) in commercial bottles is presented. Fifty-eight bottle samples from several brands and producers containing different percentages of r-PET were purchased from the market. Samples were analyzed by two spectroscopic methods: near-infrared (NIR) spectroscopy and attenuated total reflection (ATR) spectroscopy in the mid-infrared (MIR) region. No chemical pre-treatment was applied before analyses. The spectra were analyzed by partial-least squares (PLS) regression, and two models for NIR and MIR data were computed. Then, a multi-block regression was applied to join the two datasets. All models were validated by cross-validation and by excluding and projecting onto the model the replicated spectra of one sample at a time. Results demonstrated the potential of this approach, especially considering the variability of commercial samples in terms of additives, shape, or thickness of the bottles: for samples close to the centroids of the models (i.e., from 10 to 50% r-PET), the predictions of multi-block method seldom departed from the expected values of ±10%. Only for samples with 0% declared r-PET, the models showed poor prediction abilities.

1. Introduction

Plastic waste management is one of the main environmental problems that have arisen in the last few years [1]. Most plastic-manufactured goods, indeed, are thought of as single-use (e.g., bottles, straws, crockery), posing the issue of dealing with their after-use fate. It has been estimated that the world’s production of plastics reached 368 million tons in 2019, with an increase of 10 million tons from 2018 [2]. Europe alone is responsible for 16% (60 million tons) of global plastic production [2]. The uncontrolled accumulation of plastic waste causes several problems, starting with the pollution of natural areas [3,4] but also extending to an economic point of view [5].

Among plastic materials, polyethylene terephthalate (PET) is probably the most important and the most used due to its physical and chemical properties [6] in terms of lightness, resistance, transparency, flexibility, and impermeability. These properties make it an ideal material for food packaging and several other applications [7].

Recycling plastic materials, in general, is deemed the best solution to waste accumulation since it transforms waste into a newly usable artifact. The European target for plastic recycling is to reach 70% of the total waste by 2030 [8]. Such a task, however, poses new issues to researchers, starting from finding new, efficient, and clean processes to recycle plastic materials [9,10,11]. Another relevant issue is that recycled PET (r-PET) used for food packaging must not transfer residuals of its previous content or substances used during the recycling process into the new product (migration). Much attention has been paid to this, and several publications deal with this problem [12,13], in particular, considering that r-PET for food packaging may derive from PET not used for food [3,14]. Moreover, the physical properties of r-PET have been studied [15,16,17], and several possible advanced applications, other than food packaging, have been evaluated [18,19,20].

Another important problem to be faced is the quantification of r-PET into new manufactured goods. Besides the problem of migration of chemical residuals from r-PET into the food, there is also an economic aspect that influences r-PET, real or pretend: r-PET generally has a lower cost than the virgin material [21], and, at the same time, some countries economically encourage the use of r-PET, leading to scarce transparency in the declared composition mix of the final composite. Some studies have already dealt with this issue by studying, in particular, PET and polyethylene by gas-chromatography coupled to mass spectrometry (GC-MS) [21,22] and polypropylene by near-infrared (NIR) spectroscopy [23].

Two interesting works of Peñalver et al. regarded the use of chemometrics to develop a method for the quantification of r-PET in bottles. In the first one [21], they analyzed the volatile organic compounds (VOCs) of r-PET by GC-MS. These are probably present in the samples due to polymer degradation during the recycling process or as a residual from the previous life of the plastic objects. The second one [24], instead, reported the quantification of r-PET and the classification of virgin and recycled PET samples using Raman spectroscopy.

The present work explored, instead, the use of infrared spectroscopy to quantify r-PET in commercial bottles. In particular, we analyzed a set of bottle samples containing different declared amounts of r-PET with two distinct methods: NIR reflectance and attenuated total reflectance (ATR) spectroscopy, the latter working in the medium-infrared (MIR) range. It has already been shown that by adopting careful and reproducible measuring protocols, MIR-ATR can be employed for quantitative analysis [25]. An extensively used chemometric tool for processing spectroscopic data is partial least squares (PLS) regression [26], which has been applied to the two datasets both separately and jointly by Sequential and Orthogonalized-PLS (SO-PLS) regressions [27]. The application of IR spectroscopy makes the analyses very simple and only slightly destructive because the sample must be only cut to suit the instrument probe without any chemical pre-treatment. However, IR signals might not be suitable for immediately discriminating virgin PET from r-PET due to their common chemical structure. The main difference observed between the two PET typologies is, instead, the length of the polymer chains [28], besides the possible presence of trace residues. A proper chemometric analysis is essential to extract all the chemical information embedded in IR spectra, such as, for example, SO-PLS, enhancing the amount of available information by using both datasets at the same time [29]. Last, the proposed method is totally untargeted; thus, it does not require previous knowledge about the chemical nature of the species generating the signals: once validated, it might be potentially implemented by the industry as quality control to guarantee the percentage of r-PET present in their manufactured goods.

2. Materials and Methods

2.1. Bottle Samples

For the present study, fifty-eight bottle samples were collected. Fifty-four of them were used as training sets for the chemometric models, while the remaining four were randomly chosen as test sets. Of the 54 training samples, eighteen bottles were purchased from the market; one of them contained milk, five cold tea, and the other twelve drinking water. The remaining 36 bottles were purchased directly from the producers before their market placement. The bottles were produced with different percentages of declared r-PET: 0% (fifteen samples, not declaring to contain r-PET); 10% (three samples); 25% (five samples); 30% (nine samples); 50% (thirteen samples); 100% (nine samples). The percentage declared on the label was considered as the actual r-PET fraction and used as a response for the chemometric models described in the following paragraphs. The four test samples were water bottles, also in this case purchased from the market; one had a declared r-PET percentage of 0%, one of 100%, and two of 50%. They were employed to test the models and check the consistency between the results obtained with the listed batch and these samples.

All the bottles were emptied of their content (if present), rinsed, and dried. For both NIR and ATR analysis and for each bottle sample, three round portions with diameters of about 2 cm were cut from the bottles. The round portions were washed with Milli-Q grade water (Millipore, Bedford, MA, USA) and dried again prior to spectroscopic analyses.

2.2. NIR Analysis

NIR analyses were carried out with a MicroNIR OnSite-W spectrometer (VIAVI Solutions Inc., Scottsdale, AZ, USA), a portable spectrophotometer (about 250 g in weight), with two integrated vacuum tungsten lamps, an InGaAs detector covering the spectral range of 908–1676 nm, and a linear variable filter as dispersing element. The resolution was 7 nm; the integration time was set at 10 ms, with 50 scans for each spectrum, resulting in a total acquisition time of 0.25 s. Two replicates for each round plastic portion were acquired (resulting in six replicates for each bottle sample). Dark and reference samples were acquired before each sample. All analyses were carried out with the probe perpendicular to the sample and the standard.

2.3. MIR-ATR Analysis

MIR-ATR spectra were collected with a Bruker ALPHA FT-IR spectrometer (Bruker Platinum ATR, Billerica, MA, USA), with a 0.6 mm × 0.6 mm active area and HgCdTe detector. The instrument is equipped with a single-reflection diamond ATR accessory (Bruker Platinum ATR, Billerica, MA, USA). Spectra were acquired in the range of 400–1900 cm⁻¹, with a resolution of 4 cm⁻¹. The final spectrum is the mean of 64 scans for a total analysis time of 3 min. Five replicates were acquired for each sample, each time changing the probe position on the sample and recording a blank before the analysis of each new sample.

The main problem with MIR analysis in ATR mode is that the plastic sample must be as flat as possible to optimize the contact with the instrument probe (the instrumental setting of NIR analysis made it less susceptible to sample concavity). This could represent a drawback for commercial samples since sometimes bottles contain no flat parts except for the base (that, in turn, may have printed or relief portions).

2.4. PLS Analysis

Before any chemometric analysis using spectra in the IR region, particularly concerning regression, spectra pre-processing is strongly recommended [30]. Therefore, the most common pre-processing methods for NIR data and their combinations were applied: derivatization (Savitzky–Golay derivative); multiplicative scatter correction (MSC); standard normal variate (SNV) [30]; and orthogonal signal correction (OSC) [31].

The corrected NIR and MIR-ATR spectra were used to compute a PLS regression model. PLS is a consolidated chemometric method [26,32] that performs a regression using the experimental variables (in this case, IR spectra) as predictors and one or more continuous variables characterizing the samples (in this case, the label-declared percentage of r-PET) as dependent ones. The computation is carried out by calculating factors that are linear combinations of the predictors and retaining part of the information derived also from the dependent variable(s). A detailed description of the PLS algorithm is beyond the scope of the present work and can be found elsewhere [26,33]; it is important to highlight that a proper number of factors must be selected to compute and evaluate a model and to use it for predictions. This is generally chosen as the number of factors that minimizes the root mean squared error (RMSE), which is the mean (squared) difference between the known response values and the ones recalculated by projecting the samples onto the calculated model. It can be calculated both by keeping all the samples in the computed model (calibration mode) or by excluding one sample or a group of samples from the computation and then projecting onto the resulting model the excluded sample(s) (cross-validation procedure, CV). CV is generally considered a good starting point for evaluating the predictive abilities of the model before projecting real unknown samples. Both for calibration and CV, a response plot can be created, in which the known response values are reported vs. the fitted and predicted ones, respectively. The regression line calculated with these data should have a unitary slope and a null intercept as target values, indicating a perfect match between fitted-predicted and known values. The deviations from these ideal values, besides R² of the line and the PLS-model RMSE, can be used to evaluate the model performances.

Due to the absence of certified standards of r-PET mixed with virgin PET, in the present work, a general PLS model was computed to check for the reliability of the NIR and MIR-ATR methods. Then, a “leave-one-sample-out” CV was performed by computing 59 different models, each time excluding all the replicates of a bottle sample (test set) and projecting them onto the model computed by the other ones (training set). The calculated response was then compared with the label-declared percentage of r-PET. The five “unknown” samples were instead projected onto the full model, and their percentage of r-PET was calculated to compare NIR and ATR models.

Computations of all PLS models were carried out with R version 4.1.0 [34] using the library “pls” [35]. Spectra pre-treatments necessary to deal with IR spectra were carried out using the R library “prospectr” [36] and the software The Unscramber 10.4 (CAMO, Oslo, Norway).

2.5. Multi-Block Analysis

Sequential and Orthogonalized Partial Least Squares (SO-PLS) [37] is a multi-block regression method developed to sequentially extract information by several blocks of data, eliminating redundancies possibly present among the predictor blocks. The approach is conceived to combine data of different natures, allowing for the ensemble pre-processing of the signals [38]. For a two-block case, wherein two predictor matrices ($X_1$ and $X_2)$ are used to estimate a response $y$, the algorithm can be summarized as depicted in the following steps:

• $y$ is fitted to $X_1$ by PLS;
• $X_2$ is orthogonalized with respect to the X-scores extracted in 1, obtaining $X_{2,Orth}$;
• $X_{2,Orth}$ is used as a predictor to estimate (by means of PLS) the y-residuals from 1;
• The final model is estimated by combining the two sub-models:

$${y=X}_{1}B+X_{2}C+E$$

where $B$ and $C$ are the regression coefficients matrices, and $E$ the residuals of the model.

For more than two predictor blocks, the algorithm continues following the same procedure, taking care of orthogonalizing each further block with respect to all the previously modeled ones. For more details, the reader is referred to the literature [27]. All calculations related to the multi-block analysis were run in Matlab (The Mathworks, Natick, MA, USA; version 2015b) using in-house functions.

3. Results

NIR, MIR-ATR, and multi-block starting dataset were composed of 354 objects (six replicates of 58 bottle samples), 24 of which (four samples) were considered as a “test-set”. In order to find possible outliers in NIR and MIR-ATR datasets and to have the same number of objects for all analyses, spectra were first analyzed in the following way. All NIR and MIR-ATR were pre-treated by SNV, followed by an MSC carried out on the six replicates of each sample. Then, a low-level data fusion was performed, attaching MIR-ATR spectra after the NIR ones. A PCA model for each percentage of declared r-PET (0%, 10%, 25%, 30%, 50%, and 100%) was calculated, and objects falling outside the Hotelling’s ellipse at 25% significance were considered outliers and discarded from further analyses. We decided to raise the significance from the common value of 5% to 25% because the spectra showed a wide variability, mostly in their baseline, as is also supported by visual inspection. We could not be sure, however, that samples with the same declared r-PET percentage could be actually comparable, considering that these came from different brands and producers. Therefore, we decided to put a stricter decision limit in order to obtain a more reliable dataset for regressions. In this way, the datasets cleaned by outliers were composed of 261 objects; only two samples (one at 0% and one at 25% r-PET) were completely removed from the dataset, while for other samples, only some (if any) replicates were removed. All r-PET percentages were still represented by at least three samples. The original data, without previous pre-treatments and cleaned from outliers, were then used to calculate PLS models.

3.1. NIR Data

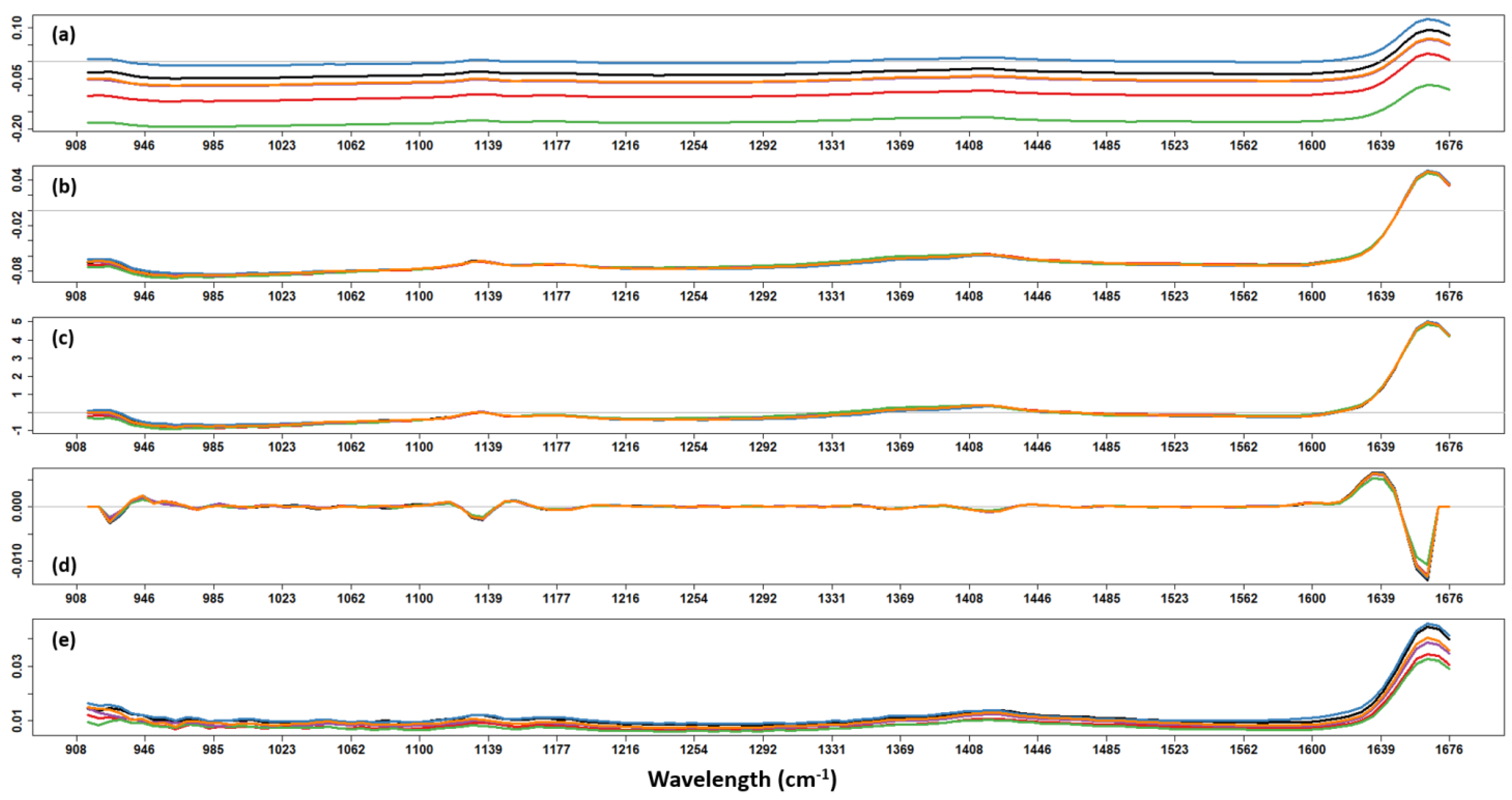
NIR data were composed of 125 variables (wavelengths ranging from 908 to 1676 nm). To find the best pre-processing method, the most common spectra pre-treatments (MSC, SNV, derivative, OSC, and their binary combinations) were independently applied to the data. Figure 1 shows the effects of single pre-treatments on the NIR spectra. The quality of pre-processing methods was evaluated by computing a PLS model after each of them and by evaluating the CV performances of each model. The best pre-processing method for NIR data was found to be MSC.

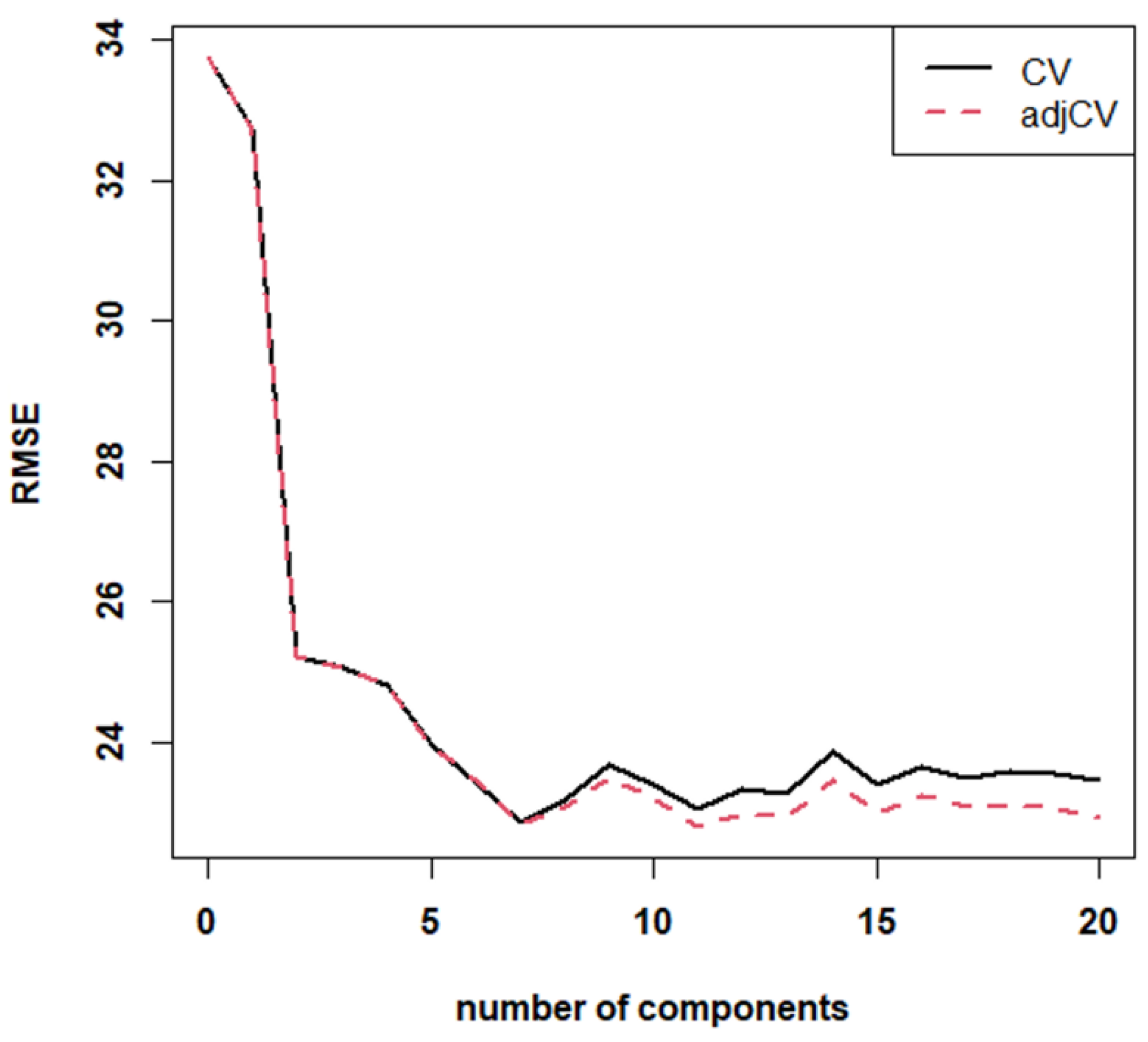
Figure 2 shows that the RMSE for the NIR model reaches a local minimum for factor 7, which is the one used for extracting the recalculated values in calibration and CV modes. Both RMSE and response plots indicate that the model has poor performance in CV. RMSE is, indeed, also quite high at its minimum (~23%), and the response plot has low R² values (0.59 in calibration and 0.32 in CV), with all slopes and intercepts significantly different from the ideal values. Such poor performances can be due to sample variability and to the fact that NIR alone might not be suitable for quantitative analysis.

However, the most interesting results for the present work are the model performances on predictions of r-PET percentages. Nonetheless, we decided to keep the PLS model to perform the “leave-one-sample-out” CV procedure on single samples. Sample-by-sample replicates were excluded from the model; PLS was recalculated and used to recalculate the fraction of r-PET in the excluded objects. Results of such computations on all samples are reported in

Table A1. Known and PLS-predicted values, with the corresponding standard deviations, for all samples projected onto the three models (NIR, MIR-ATR, and multi-block). Overall mean and median differences between known and predicted values are also provided.

Sample	Known r-PET (%)	NIR Model	MIR-ATR Model	Multi-Block Model
SM08	0	32 ± 6	51 ± 16	34 ± 6
SM19	0	23 ± 5	34 ± 13	22 ± 5
SM20	0	43 ± 2	58 ± 13	48 ± 4
SM26	0	26 ± 4	36 ± 16	23 ± 7
SM28	0	34 ± 9	39 ± 14	28 ± 12
SM29	0	18 ± 5	31 ± 13	9 ± 7
SM36	0	24 ± 4	18 ± 11	23 ± 7
SM38	0	26 ± 4	12 ± 24	25 ± 6
SM39	0	30 ± 6	37 ± 14	27 ± 7
SM40	0	34 ± 7	35 ± 14	34 ± 9
SM46	0	30 ± 4	28 ± 10	27 ± 5
SM50	0	24 ± 4	13 ± 29	17 ± 4
SM51	0	21 ± 4	23 ± 22	17 ± 6
SM53	0	1 ± 3	8 ± 3	−4 ± 12
SM49	10	8 ± 11	9 ± 13	4 ± 11
SM52	10	13 ± 12	−2 ± 30	15 ± 22
SM54	10	3 ± 9	5 ± 34	−6 ± 13
SM01	25	35 ± 4	39 ± 10	47 ± 4
SM06	25	30 ± 3	27 ± 4	38 ± 3
SM43	25	9 ± 7	38 ± 22	15 ± 10
SM47	25	32 ± 5	43 ± 5	36 ± 6
SM10	30	51 ± 6	46 ± 11	54 ± 6
SM11	30	35 ± 10	34 ± 16	41 ± 12
SM13	30	15 ± 7	30 ± 10	28 ± 9
SM21	30	27 ± 11	38 ± 16	33 ± 15
SM31	30	47 ± 17	41 ± 8	46 ± 13
SM34	30	16 ± 4	19 ± 21	9 ± 14
SM42	30	39 ± 7	19 ± 13	35 ± 10
SM44	30	19 ± 3	42 ± 16	24 ± 4
SM48	30	25 ± 6	45 ± 8	18 ± 8
SM02	50	94 ± 9	41 ± 5	82 ± 6
SM07	50	36 ± 7	29 ± 12	49 ± 9
SM09	50	38 ± 2	33 ± 14	45 ± 2
SM12	50	35 ± 7	38 ± 17	43 ± 7
SM16	50	28 ± 13	28 ± 17	44 ± 21
SM18	50	34 ± 6	38 ± 20	40 ± 6
SM22	50	29 ± 7	37 ± 7	39 ± 7
SM25	50	18 ± 6	47 ± 10	23 ± 10
SM30	50	27 ± 4	24 ± 11	27 ± 4
SM32	50	39 ± 6	46 ± 15	38 ± 6
SM33	50	26 ± 4	33 ± 13	25 ± 7
SM37	50	23 ± 8	15 ± 11	23 ± 10
SM41	50	12 ± 6	−8 ± 10	2 ± 12
SM03	100	103 ± 9	56 ± 18	86 ± 5
SM04	100	105 ± 4	94 ± 43	87 ± 2
SM05	100	95 ± 6	113 ± 45	82 ± 4
SM14	100	116 ± 12	74 ± 22	86 ± 7
SM15	100	106 ± 31	56 ± 45	88 ± 18
SM23	100	64 ± 3	55 ± 5	74 ± 4
SM24	100	68 ± 7	58 ± 8	79 ± 10
SM27	100	29 ± 7	54 ± 15	41 ± 5
SM45	100	64 ± 4	82 ± 11	65 ± 3
Mean difference |Known−Predicted|		19.7	21.3	18.5
Median difference |Known−Predicted|		17.4	16.7	16.4

in Appendix A.

Table 1. Mean PLS prediction on NIR dataset for each r-PET percentage. Mean and standard deviations (Std. Dev.) are calculated over all the objects of each percentage.

Known r-PET %	Mean Predicted	Std. Dev. Predicted
0	26.1	9.7
10	8.1	5.1
25	26.4	12.0
30	30.4	13.2
50	33.7	19.6
100	83.3	28.5

, instead, reports the PLS results obtained for each r-PET percentage in terms of means and standard deviations (calculated over all the objects). The results in Table 1 show some drawbacks of the method but also some encouraging results. The mean recalculated values are generally not far from the expected ones except for 0%, although standard deviations are generally high. Table A1 confirms that the reason mainly resides in some specific samples, whose recalculated percentage is far from the expected (e.g., sample “SM02”, expected 50%, predicted 93.7%). However, considering the absolute values of the differences between known and recalculated values, their mean is 19.7%, while the median is 17.4%. It indicates that there is generally a satisfactory agreement between expected and recalculated r-PET percentages.

Unexpectedly, the main gap in the model concerns virgin PET (0%) samples. Table 1 shows that the mean recalculated value is 26.1%, and from Table A1, it can be seen that only one sample out of 15, “SM53”, yields a satisfactory prediction, while most of the other recalculated values range between 20 and 40%. We also observed the score plot of both PCA and PLS, also considering different pre-treatments (not shown), but in all cases, no clear discriminations between the 0% and the other samples were observed.

3.2. MIR-ATR Data

MIR-ATR spectra were acquired in the mid-IR range from 1900 to 400 cm⁻¹. We decided not to analyze the full mid-IR range, from 4000 cm⁻¹, because most of the signals between 4000 and 1800 cm⁻¹ turned out to be flat for all samples (or with small bands due to residual humidity), except for a band between 3000 and 2800 cm⁻¹ with peaks attributable to C-H stretching. However, this band was not clearly visible in most of the spectra; thus, it was discarded. The final dataset was then composed of 735 variables. Again, the most common pre-treatments and their combinations were applied to the dataset without outliers (Figure 3), and, in this case, the combination SNV followed by Savitzky–Golay second derivative (using a third-degree polynomial function and a window of five variables) (Figure 3f) was considered the best.

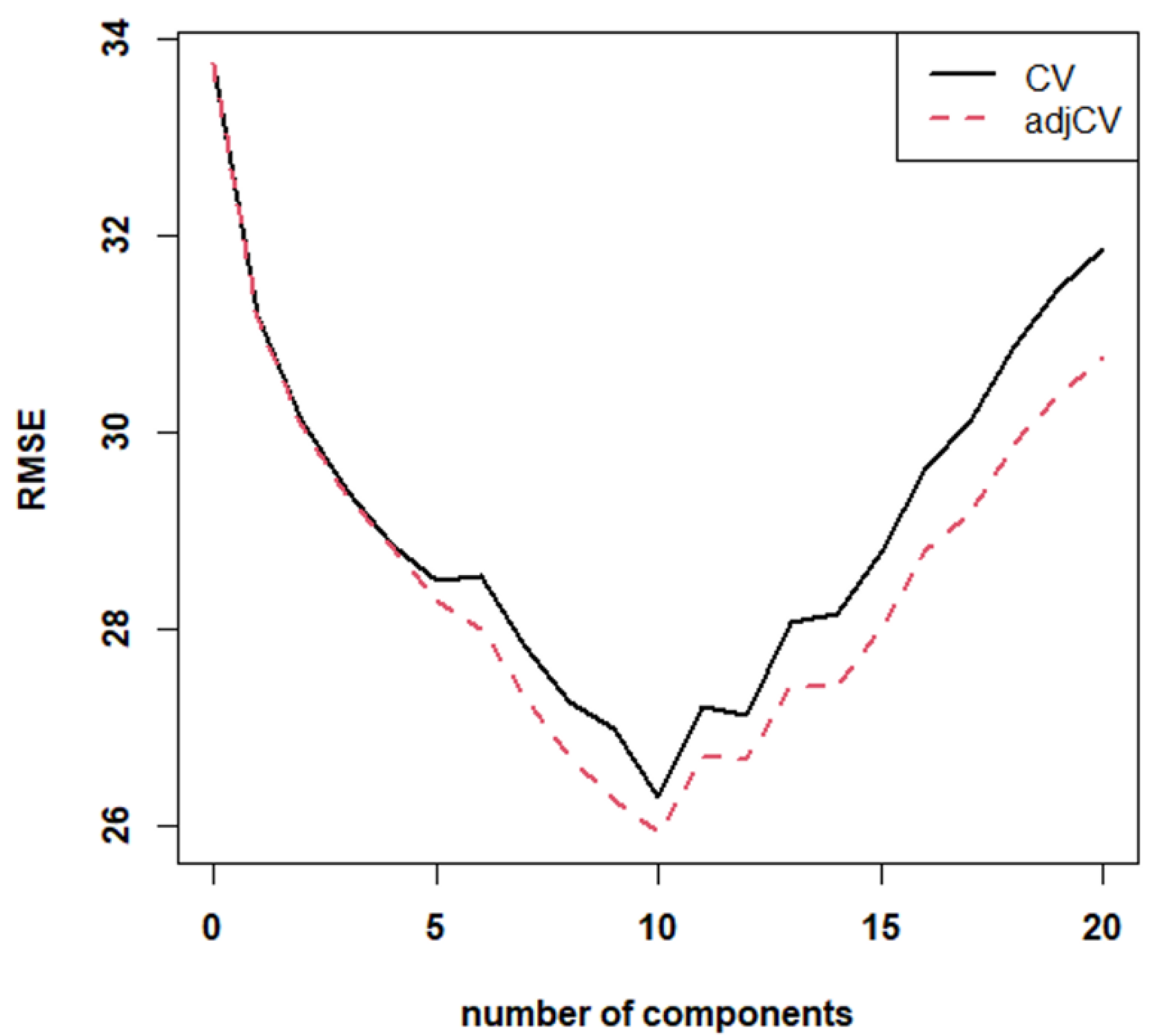
The chemometric procedure is the same as previously applied to NIR data, where the first step is a general PLS model. Compared to the NIR model, the MIR-ATR one does not show significant differences. The best observed RMSE (Figure 4) is higher than that calculated for the NIR model (~27%), with a higher number of factors (11). Moreover, the corresponding response plot shows worse R² both in calibration (0.59) and in CV (0.32). Slopes and intercepts are again significantly different from the ideal values of 1 and 0. Despite the poor performances in cross-validation, this model was also used alone to predict the analyzed samples. Results are reported in

Table 2. Mean PLS prediction on MIR-ATR dataset for each r-PET percentage. Mean and standard deviations (Std. Dev.) are calculated over all the objects of each percentage.

Known r-PET %	Mean Predicted	Std. Dev. Predicted
0	30.2	14.4
10	4.0	6.0
25	36.6	6.8
30	35.0	10.4
50	30.8	14.6
100	71.4	21.2

as mean PLS results for each r-PET percentage and in Table A1, with the predicted values of each sample.

Table 2 shows that the prediction abilities are, in general, close to those observed for the NIR model, although a little poorer. Relative standard deviations are also close to those observed for the NIR mode. The results observed for the single samples in Table A1 are also similar to those observed for NIR, with some worse predictions but also with some better predictions. The mean value of absolute differences between expected and recalculated r-PET percentages is 21.3%, and the median is 16.7%. Also, in this case, the drawback concerning the virgin PET samples was observed, which never showed satisfactory predictions (it could also be an explanation for the very poor R² of the general model).

3.3. Multi-Block Analysis

SO-PLS was applied to analyze the NIR and MIR blocks mentioned in Section 3.1 and Section 3.2, using different signal pre-treatments for the diverse data matrices. In total, eight blocks were exploited, i.e., NIR data pre-treated by OSC ($X_1$), SNV ($X_2$), first derivative ($X_3$), and second derivative ($X_4$), and MIR signals were pre-processed with the same pre-treatments in the same order (corresponding to the fifth, sixth, seventh, and eighth blocks: $X_5$; $X_6$; $X_7; X_8$). As described above, several cross-validated models were created in a “leave-one-sample-out” fashion: iteratively, for each set of replicates collected on individual samples, all the available spectra, except for those associated with a single specimen of PET, were used as the training set for calibration, whereas the replicated signals belonging to the sample left out were used as the test set for validation. The optimal calibration model has been chosen to inspect the cross-validated RMSECVs through a Mage plot, and it was the one built to extract two and one LVs from $X_1$ and $X_3$, respectively. Results, expressed in terms of r-PET, mean predicted values, and their standard deviations, are reported in

Table 3. Mean SO-PLS prediction. Mean and standard deviations (Std. Dev.) are calculated over all the objects of each percentage of r-PET.

Known r-PET %	Mean Predicted	Std. Dev. Predicted
0	23.5	12.1
10	4.2	10.4
25	34.1	13.8
30	32.1	13.9
50	36.9	18.7
100	76.5	15.3

(mean values) and Table A1.

It has to be noted that MIR blocks have never been selected as the best combination of input data, indicating that this platform does not provide further relevant information with respect to NIR.

In general, the predictive capability of the various models is satisfying. It can be noted that the predictions at the edges of the r-PET range are less accurate than those at 25, 30, and 50% of r-PET.

3.4. Comparison of the Three Models

The cross-validation and “leave-one-sample-out” procedure showed that NIR and multi-block had the best performances in predicting r-PET percentage in bottle samples. To further evaluate the models, four samples not involved in the computation of the models were projected onto each of them: two of them were chosen with extreme values (0 and 100%, respectively), and the other two were chosen with the intermediate value of 50%. The results are reported in

Table 4. PLS predictions for the unknown samples based on the three models.

	Known r-PET (%)	NIR Model	MIR-ATR Model	Multi-Block Model
SM55	0	11 ± 6	31 ± 11	9 ± 9
SM56	100	79 ± 12	59 ± 27	85 ± 9
SM57	50	70 ± 6	68 ± 26	85 ± 4
SM58	50	63 ± 22	75 ± 32	73 ± 17

, in which mean and standard deviations (based on six replicates) are shown. These samples were used to simulate a real case in which the percentage of r-PET must be analytically confirmed. Table 4 shows that the MIR-ATR model has the poorest performances, both in terms of predictions and considering the variability bringing high-standard deviations. Instead, good consistency between multi-block and NIR models can be observed. The multi-block model shows the best performance for the extreme expected values, interestingly also for the 0%-sample (SM55). The two 50%-samples are slightly over-predicted by all samples, with NIR showing the best performances, although with a higher standard deviation compared to multi-block.

4. Discussion

The regression models so far presented have shown contrasting results. On the one hand, all PLS models have poor descriptive abilities, but on the other hand, Table A1 shows that the recalculated r-PET values for most samples are close to the expected ones, although all 25-, 30-, and 50%-samples have close recalculated values for all models in the range of 30–50%. Most 100%-samples, except one, are instead recalculated in the range of 60–110%, therefore, with satisfactory results, also considering that no samples have been found in the market with declared r-PET percentage in the range of 50–100%. Moreover, Table 4 shows the satisfactory predictive abilities of the models, at least in the NIR and multi-block cases. The only percentage of the “class” with poor performances, and for all models, remains at 0%.

We do not have a definitive explanation for such poor performances. One hypothesis is that virgin samples are somehow different from the others, perhaps in the mean length of the polymeric chain [6], since these samples did not undergo any recycling processes. It was observed in previous studies [5] that virgin and recycled PETs have different physical and chemical characteristics. Such difference might not be clearly visible in the spectra but may be important for the PLS model and, perhaps, magnified by the spectra pre-treatment processes. Moreover, we cannot exclude that the inner surface of examined PET bottles was treated either by functionalization or by filming for optimal preservation of beverages [39]. These treatments may modify in an unpredictable way the overall spectrum due to the variety of treatments available on the market and whose type is not declared on the labels. A more in-depth analysis is necessary to face this issue, possibly involving further analytical methods, such as GC-MS, and it is postponed to future works.

From a chemical and chemometric point of view, finally, NIR analysis demonstrated more reliability than MIR-ATR. SO-PLS, indeed, selected only blocks from NIR to compute the final model. Predictions on unknown samples also showed higher variability in the MIR-ATR case. Besides the possible chemical treatment that might affect the MIR region more than the NIR one, another possible explanation could be a geometric one. As has already been stated, ATR analysis requires good contact between the sample and the instrument probe. Although caution has been kept during the analysis, i.e., using a spatula between the sample and the instrument press to further press the sample, such contact may not be fully reproducible for concave samples as most of the bottle portions used in the present work are.

It must be kept in mind, however, that the present work was carried out with commercial samples, considering the r-PET percentage declared on the label as the expected one. The 0%-samples, however, are the ones with no declaration on the label of using r-PET, considering that no brand declares to use only virgin plastic, but there should be no interest in using it without declaring it. With these premises, with no full certainties about the expected values, it is not surprising that the “leave-one-sample-out” recalculated values are not always in accordance with the expectations and mean differences between expected and recalculated values of around 20% (Table A1) can be considered satisfactory. In the research field of r-PET analysis, to the authors’ knowledge, there is only another work from Peñalver et al. [24] dealing with the quantification of r-PET in manufactured goods with spectroscopic methods. In that case, Raman spectroscopy was used on 400 PET samples with different r-PET percentages, obtaining regression of a model with higher R² (0.911) to those obtained in the present work but comparable RMSE (17.9) to ours. The predictive abilities of the model were better than ours, but also, in that case, with standard deviations in the order of 15–20%, which are again comparable with our results. Other works [21,40] demonstrated the capability of GC-MS in discriminating between virgin and recycled PET. Further methodological validation of our proposed method could foresee a direct comparison of the different approaches to suggest their combination or alternative use. In the work from Peñalver et al. [21], orthogonal PLS regression on VOCs concentrations dataset was used, obtaining a model with higher R² (0.978) and lower RMSE (9.27) compared to our results but with a lower number of samples (23, with three replicates). Bhattarai et al. [40], instead, did not calculate a regression model for the r-PET quantification but demonstrated that the presence of some MS fragments (mainly due to oligomers) and also some MIR-ATR peaks could be used to discriminate recycled from virgin PET. The latter conclusion was drawn by observing slight differences in some peak intensities attributed to a lower crystallinity degree of r-PET.

In the absence of r-PET standards, which is a huge limitation for the development of a quantitative methodology, GC-MS can be evaluated as a method to validate at least virgin and recycled PET samples. Quantification by spectroscopic analyses may be carried out at a later time, perhaps removing the virgin samples from the model (yet “validated” as a virgin by GC-MS) and focusing only on different percentages of r-PET. Chemometrics and data pre-treatments must be extensively used to highlight the slight spectra differences due to the different recycling amounts.

5. Conclusions

Fifty-nine PET bottles were analyzed by NIR and MIR-ATR spectroscopy in order to quantify the content of recycled polyethylene terephthalate. Preliminary regression models based on NIR and MIR-ATR spectra, used both independently from each other and jointly, were computed and validated by cross-validation and by a “leave-one-sample-out” validation. Results are promising because good predictions were obtained, in large part, by the NIR model and also by the MIR-ATR one. Considering all cross-validated results, as reported in Table A1, the overall mean difference between expected and recalculated values is 19.7% for NIR data and 21.3% for MIR-ATR. The application of a multi-block method such as SO-PLS optimized the predictions, reducing the overall mean difference to 18.5% but using only NIR data. NIR spectroscopy seems, therefore, to be the most promising technique for further applications. The main weak point in the model was observed for virgin plastic samples, for which the poorest predictions were observed. More samples will be acquired in the future, and a different chemometric approach, eventually a classification, will be applied to evaluate the reasons for such differences. Moreover, the models and the results were found to be not brand-dependent. In all computed models, indeed, all samples from several brands and different percentages of declared r-PET were used, and the results did not depend on the presence or absence of a specific brand. Therefore, such an approach can be generally used for the quantification of r-PET and also as a screening test in the industry. Our method also has the advantage of being almost non-destructive and does not require chemical pre-treatments on plastic samples; therefore, it is easy, low-cost, low-time-consuming, and clean. Moreover, it must be further underlined that the present method was based on commercial samples; thus, its application to standards of pure virgin and recycled PET would certainly increase its stability and reliability.