Thermal Hydraulics and Solid Mechanics Multiphysics Safety Analysis of a Heavy Water Reactor with Thorium-Based Fuel

Abstract

Growing environmental awareness has renewed interest in thorium as a nuclear fuel, underscoring the need for further studies to evaluate how reactors perform when conventional fuels are replaced with thorium-based alternatives. In this study, thermal hydraulics and solid mechanics computations were simulated using COMSOL multiphysics to investigate the safe operating conditions of a heavy water reactor with thorium-based fuel. The thermo-mechanical analysis of the fuel rod under transient heating conditions provides critical insights into strain, displacement, stress, and coolant flow behavior at elevated volumetric heat sources. After 3 s of heating, the strain distribution in the fuel exhibits a high-strain core surrounded by a low-strain rim, with peak volumetric strain increasing nearly linearly from 0.006 to 0.014 as heat generation rises. Displacement profiles confirm that radial deformation is concentrated at the outer surface, while axial elongation remains uniform and scales systematically with power. The resulting von Mises stress fields show maxima at the outer surface, increasing from ~0.06 to 0.15 GPa at the centerline with higher heat input but remaining within structural safety margins. Cladding simulations demonstrate nearly uniform axial expansion, with displacements increasing from ~0.012 mm to 0.03 mm across the investigated power range, and average strain remains negligible (≈10⁻⁴), while mean stresses increase moderately yet stay well below the yield strength of zirconium alloys, confirming safe elastic behavior. Hydrodynamic analysis shows that coolant velocity decreases smoothly along the axial direction but maintains stability, with only minor reductions under increased heat sources. Overall, the coupled thermo-mechanical and fluid-dynamic results confirm that both the fuel and cladding remain structurally stable under the studied conditions. By using COMSOL’s multiphysics capabilities, and unlike most legacy codes optimized for uranium-based fuel, this work is designed to easily incorporate non-traditional fuels such as thorium-based systems, including user-defined material properties, temperature-dependent thermal polynomial formulas, and mechanical response.

1. Introduction

Thorium has been viewed as a prospective reactor fuel since the nuclear power sector emerged in the 1950s, yet—despite worldwide initiatives—its advancement has consistently lagged behind that of uranium-based fuels. Today, interest in thorium has risen again due to the drive to develop safe, clean nuclear fuels capable of addressing modern power generation challenges, and its abundant reserves further underscore its potential to meet the rising global demand for energy [1,2]. Consequently, significant research has focused on investigating the replacement of uranium fuel with thorium as a means to reduce reliance on the scarce uranium fuel. Monte Carlo N-Particle eXtended (MCNPX) code version 2.7, with the ENDF.VII cross-section library, was used to study the neutronic performance of thorium-based fuel types [(_0.944Th, U)O₂, (_0.955Th, ²³³U)O₂, and (_0.934Th, rgPu)O₂] as alternatives to UO₂. It demonstrated good viability as it achieved acceptable safety parameter values and provided a favorable power distribution throughout the fuel assembly compared to UO₂ [3]. Incorporating 15% TRUO₂ into an 85% Th-²³³UO₂ fuel for Pebble Bed Modular Reactor (PBMR-400) optimizes neutronic performance by extending the fuel cycle, offering potential waste reduction and showing good environmental benefits [4]. Using a 3D heterogeneous MCNPX model, researchers evaluated thorium fuel for the Gas Cooled Fast Reactor (GCFR-400) and found that the proposed fuel exhibits promising neutronic performance with satisfactory control and safety parameters throughout its burnup [5]. Thorium-based fuels—whether blended with High Enriched Uranium (HEU), Low Enriched Uranium (LEU), or ²³³U or formulated as MOX/mononitride—deliver acceptable thermal neutron fractions for flat power density, lower fuel temperatures, improved reactivity coefficients, reduced plutonium and minor actinide production, and enhanced proliferation resistance [6,7,8,9,10]. The analysis of (Th_xU_1−x)N fuel in both infinite and compact reactor models indicates that thorium additions maintain criticality, extend reactor service life by reducing k_eff decline and enhancing ²³³U production, and introduce a potential diversion risk due to proliferation vulnerabilities [11]. Based on state-of-the-art reactor designs, it is concluded that thorium-based molten salt small modular reactors represent the most promising technical pathway to advance nuclear energy into a new era—meeting market demands while ensuring maximum safety at an affordable capital cost [12].

Designing a reactor core that meets operational requirements remains one of the most significant challenges in reactor physics, where the quest for effective core optimization methods that ensure safety and improve economic efficiency has long been a central focus. Additionally, simulating nuclear fuel behavior is crucial for licensing and interpreting experiments with new fuels as it involves evaluating temperature distributions, velocity profile, and stresses. Finite Element Modeling (FEM) plays an important role in the design, safety analysis, and operation of nuclear reactors because it incorporates multiple physics modules such as thermal, structural, and fluid flow. A fully coupled, time-dependent multi-physics model was developed using COMSOL Multiphysics 4.2a to analyze the single-channel behavior of a Lead Fast Reactor (LFR) under both steady-state and transient conditions [13]. The model integrated neutronics, thermal fluid dynamics, and thermal–elastic effects; enabled accurate prediction of reactivity feedbacks without relying on corrective factors; and was validated against Monte Carlo simulations using Serpent(version 1.1.17). SERPENT is a 3D, continuous-energy Monte Carlo code for neutron and photon transport, developed at VTT Technical Research Centre of Finland in 2004. It supports stand-alone burnup simulations, lattice physics, group-constant generation, and multi-physics coupling for reactor analysis, shielding, fusion applications, and more. A steady-state thermal–mechanical safety analysis of a 0.5 MWth heat pipe-cooled, graphite-moderated micro reactor was conducted using ANSYS Fluent and ANSYS Mechanical, focusing on temperature, heat pipe loads, and structural stresses during normal operation and heat pipe failure scenarios. The analysis showed that the design remains within safety limits under most conditions, and two design modifications were proposed—thermal paste and non-uniform heat sink conditions—to reduce thermal stresses in critical failure cases [14]. A two-dimensional thermomechanical coupling model of a heat-pipe-cooled space-reactor core was built in COMSOL multiphysics to calculate key heat transfer and structural mechanics parameters under both steady-state and accident conditions and to evaluate the core’s thermal safety performance. The analysis shows that failure of a single heat pipe at any location poses no safety risk. However, thermal stress exceeds the allowable limit if two heat pipes fail at the core edge, and with three failed heat pipes, it surpasses the limit even in the well-cooled central region, raising the local maximum temperature to 1959.8 K [15,16]. Coupled neutronics, thermal hydraulics, and thermo-mechanics steady-state COMSOL analysis of a molten salt fast reactor enabled an accurate assessment of reactivity feedbacks and fuel behavior in a fully liquid-fueled fast reactor configuration [17,18].

Extensive thermal hydraulics and solid mechanics safety analyses have been conducted for CANDU reactors to demonstrate pressure tube creep effects and aging-induced and high-temperature deformation behaviors. A thermal hydraulics single-channel analysis combined with post-Critical Channel Power (CCP) accident evaluation was proposed to quantify performance differences between fresh and aged CANDU-6 cores, showing that although aging reduces channel flow and CCP, up-to-date trending data and recalibrated safety analysis inputs preserve regulatory margins. This methodology provided realistic, plant-specific safety assessments that explicitly account for aging-induced deformation and hydraulic effects in long operating reactors [19]. Using finite element modeling integrated with an artificial-neural-network-based creep law, the authors computed the time-dependent stress relaxation in the flaw process zone of Zr-2.5Nb pressure tubes, revealing that creep leads to a 30–45% reduction in peak stress at flaw tips over two years, mitigating the driving force for cracking initiation and confirming that stress relaxation is crucial for maintaining the structural integrity of aged tubes [20]. The evaluation of critical heat flux (CHF) sensitivity to fuel-element diametral strain and pressure tube creep in CANDU bundles showed that as fuel-element diameters increase, inter-rod gaps narrow, degrading coolant distribution and causing earlier dry out. Consequently, dry out power decreases with increasing strain. For pressure tube creep (≈4% diametral expansion), both simulations and experiments indicated a 10–30% reduction in dry out power relative to nominal tubes, confirming that geometric deformation—whether from tube creep or rod strain—reduces CHF and overall heat transfer margins [21]. A finite-volume deformation analysis of Zr-2.5Nb pressure tubes simulated ballooning and Calandria-tube contact under severe accident conditions. Using temperature-dependent creep laws within an explicit 3D stress–strain framework, the model reproduced experimental ballooning behavior and showed that localized high-temperature creep drives rapid radial expansion and pressure-tube–Calandria-tube contact once the thermal threshold is exceeded, emphasizing the need for coupled thermo-mechanical analysis in CANDU safety evaluations [22,23]. Collectively, these studies indicate that current safety analyses remain partially decoupled—thermal hydraulics predictions rarely update structural deformation in real time, while solid mechanics models seldom ingest evolving flow and temperature fields. Ryu et al. (2023) developed the multi-physics coupled model to analyze CCP under pressure tube deformation such as sagging or wall thinning revealed that even with large or complex deformations, CCP reduction remained small once neutronic, thermal hydraulics, and structural feedbacks were coupled. Moreover, sagging effects on CCP differed from intuitive expectations as flow redistribution and power feedback partially compensated for geometric degradation, demonstrating the value of integrated multi-physics modeling over simplified analyses [24]. Finally, Lee et al. (2011) applied the Bundle Position-Wise Linear Model to predict pressure tube diametral creep in CANDU reactors using parameters such as fast-neutron fluence, heat transport system temperature, and effective full-power days. The model achieved an error of ~0.1 mm, capturing position-dependent deformation, especially the higher creep at outlet-side bundles. Although it outperformed global linear and plant design models, its empirical linear nature limits extrapolation and coupling with mechanistic creep or thermal hydraulics effects, reinforcing the need for integrated, physics-based frameworks for long-term safety analysis [25]. Therefore, advancing CANDU safety assessment requires fully coupled thermo-hydraulics and structural mechanics models capable of evolving channel geometry, coolant velocity, and material degradation under realistic transient conditions. Moreover, evolving reactor operation strategies and potential introduction of alternative fuels such as thorium demand a reassessment of heat transfer, mechanical stress, and safety margins. To the best of our knowledge, no prior study has performed a coupled thermal hydraulics and solid mechanics analysis using COMSOL multiphysics in transient mode and under different heat flux conditions for a single thorium-based CANDU fuel rod in contrast to existing works on uranium-based CANDU reactors.

Regarding the experiments, thorium-based fuels have indeed been fabricated and irradiated in the CANDU/PHWR framework, with campaigns centered on fuel cycle analysis, irradiation testing, fuel performance and post-irradiation examination, as documented by Boczar [26], by Prasad et al. for thorium bundles in Indian PHWRs [27], and in Worrall’s work on nuclear, capsule-scale thermal modeling [28]. However, none of these studies report dedicated experimental, channel-scale, or core-scale validation of coupled thermal hydraulics and solid mechanics behavior for thorium-fueled CANDU channels, which motivates our purely computational multiphysics approach.

In this study, COMSOL multiphysics was employed to carry out coupled thermal hydraulics and structural analyses, evaluating the safe operating limits of a heavy water reactor fueled with thorium. A transient model combined the Heat Transfer in Solids and Fluid Flow interfaces for heat conduction and fluid dynamics calculations, and the solid mechanics interface was used for the structural response. Thermo-mechanical and hydrodynamic simulations of a thorium-based fuel rod subjected to transient volumetric heating (from 119 to 245 MW m⁻³ over 3 s) reveal stable structural and coolant responses under elevated power densities. The fuel experiences a characteristic high-strain core, with centerline volumetric strain increasing nearly linearly from 0.006 to 0.014 while remaining axially uniform along the heated 0.5 m segment. Total displacement grows from ~0.004 mm to ~0.012 mm at the surface and from ~0.015 mm to ~0.04 mm along the axis, confirming that radial constraint by the cladding limits central motion. Mechanical loading is dominated by differential thermal expansion, producing annular von Mises stress fields that rise from 0.06 to 0.15 GPa at the center and 0.04 to 0.1 GPa at the surface, yet remain comfortably below zirconium alloy yield strengths. The cladding itself expands almost uniformly, with axial displacement increasing from ~0.012 mm to ~0.03 mm, the average strain being near 10⁻⁴, and mean stress limited to 0.035–0.04 GPa, all well within elastic and design margins. Coolant hydrodynamics remained robust throughout the transient, and upward flow showed more stable condition, with only small velocity reductions. Collectively, these results confirm that the combined fuel–cladding system maintains mechanical integrity and coolant stability under rapid power ramps to at least 245 MW m⁻³, providing critical design data for next-generation heavy water reactors employing thorium based fuels.

2. Materials and Methods

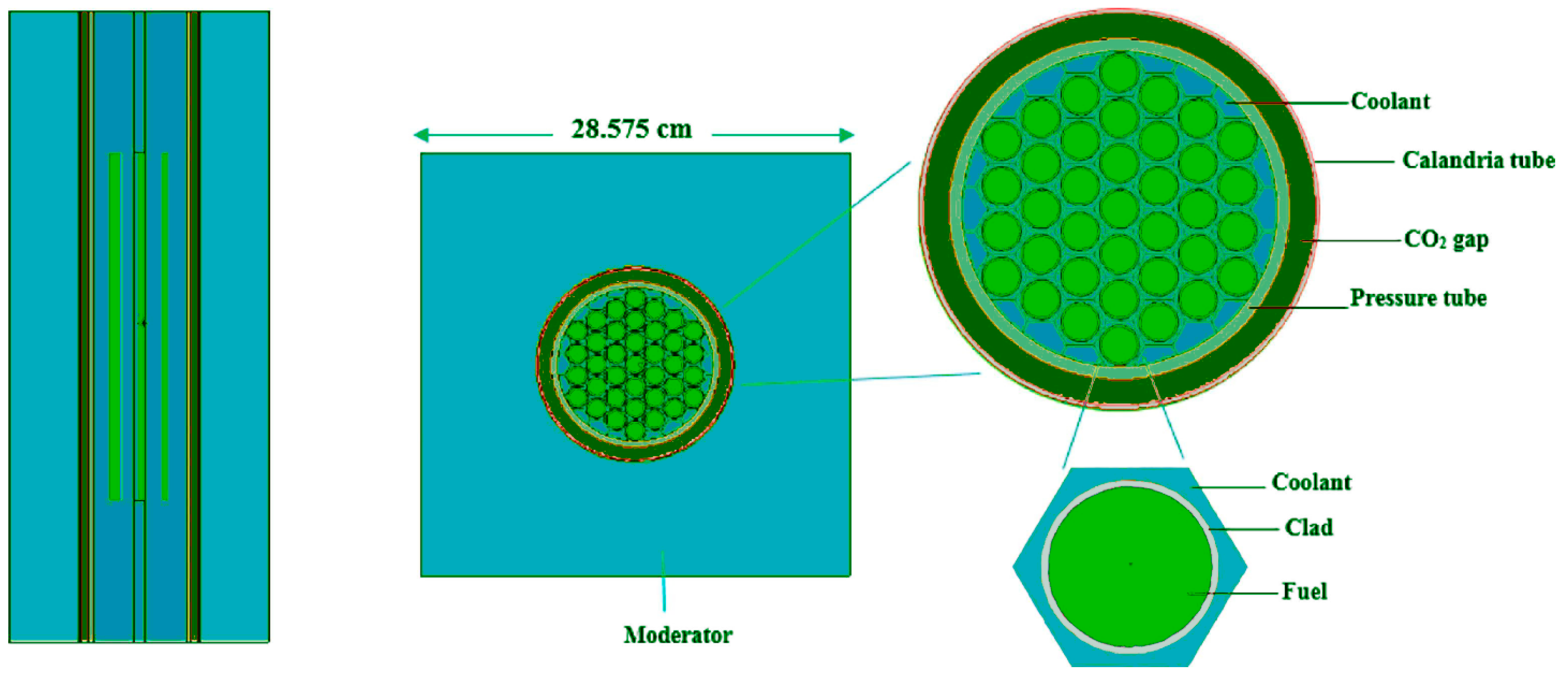
Thermal hydraulics and solid mechanics calculations can be performed using the radial power distribution obtained from the neutronic analysis. The results of the neutronic calculations reported in [29] were used as input for our calculations. The reactor core is housed within a horizontal cylindrical vessel made of stainless steel. Inside this vessel, which serves as a neutron moderator, are 380 fuel channels submerged in heavy water. The fuel channels are arranged in a square lattice with a spacing of 28.575 cm (Figure 1). Each channel includes a pressure tube made of zirconium–niobium alloy, encased within a zircaloy-2 calandria tube, and connected at both ends by stainless steel fittings. Spacers are used to support the pressure tube and maintain its separation from the calandria tube. The space between these tubes is filled with carbon dioxide gas, serving as thermal insulation to reduce heat loss. Every fuel channel holds 12 identical fuel bundles, each 49.53 cm long, with each bundle containing 37 fuel rods arranged in a circular ring configuration. Each fuel rod consists of 30 fuel pellets enclosed within a cladding tube made of zirconium alloy. The design parameters and dimensions of the reactor core can be found in

Table 1. The design parameters and dimensions of the reactor core.

Parameter	Value
Fuel channel lattice geometry	Square
Fuel channel pitch	28.575 cm
Pressure tube material	Zr-2.5Nb
Pressure tube thickness	0.4343 cm
Calandria tube material	Zircalloy-2
Calandria tube thickness	0.1397 cm
Fuel material	(Th, 233U)O2
Cladding material	zircalloy-4
Cladding thickness	0.04 cm
Number of fuel elements per bundle	37 pin
Fuel pin lattice geometry	Hexagonal
Fuel pin pitch	1.4885 cm
Fuel element height	49.53 cm
Moderator material	D2O
Coolant material	D2O

.

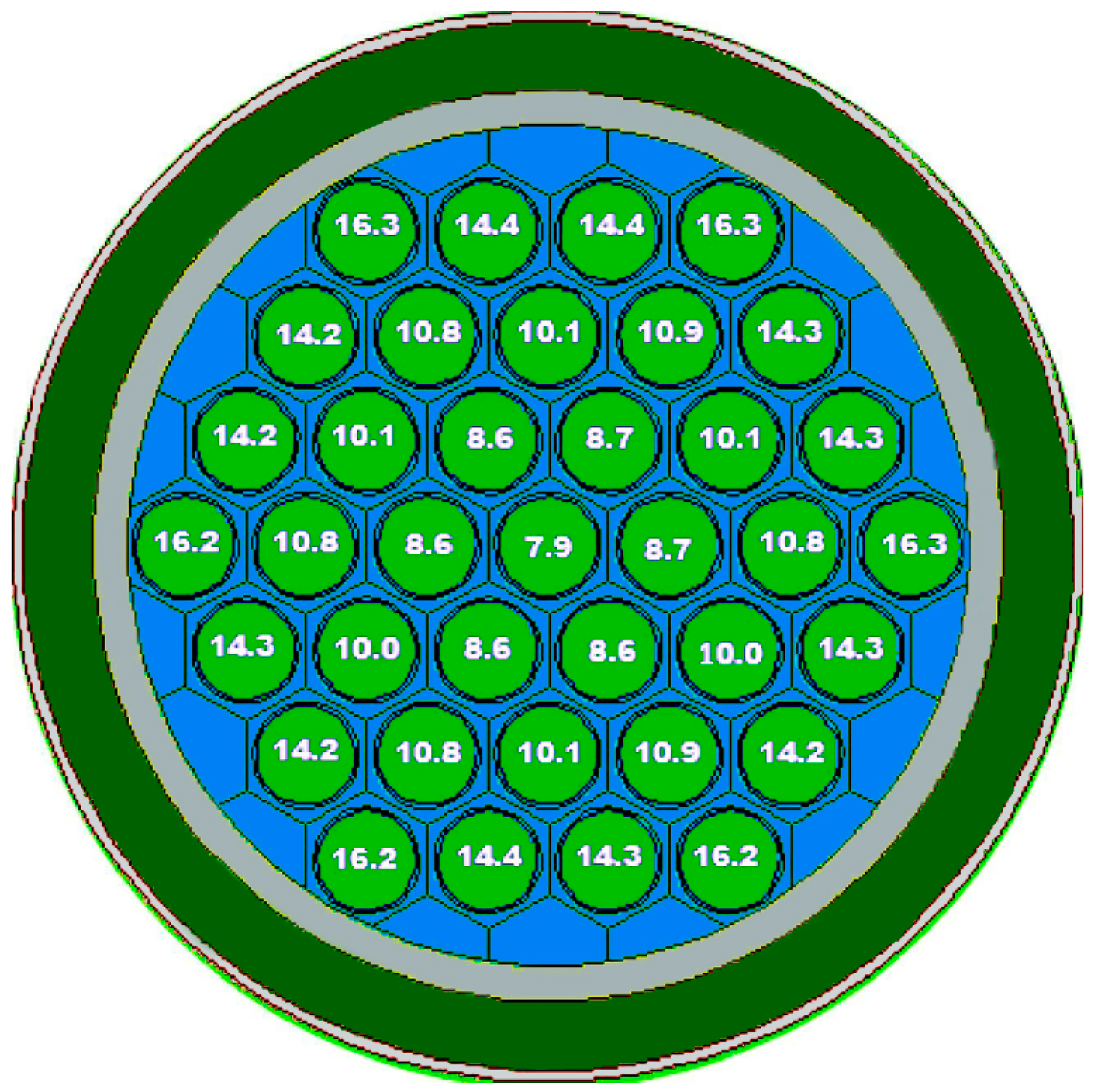
Because all fuel bundles and channels in the core are symmetrical, a single fuel bundle was modeled to represent the neutronic behavior of the fuels under investigation. Figure 2 illustrates pin power distribution through fuel bundle, which is obtained from neutronics calculations.

From the power distribution, we can identify the hottest rod, where the most limiting and safety-critical conditions in the reactor core are present. The aim is to demonstrate these conditions through simulations. For comparison, single fuel rods operating at the maximum, median, and minimum power levels were individually analyzed (

Table 2. Converted radial power values to heat source for the maximum, median, and minimum power levels.

Radial Power, kW	Heat Source, MW/m3
16.3	245
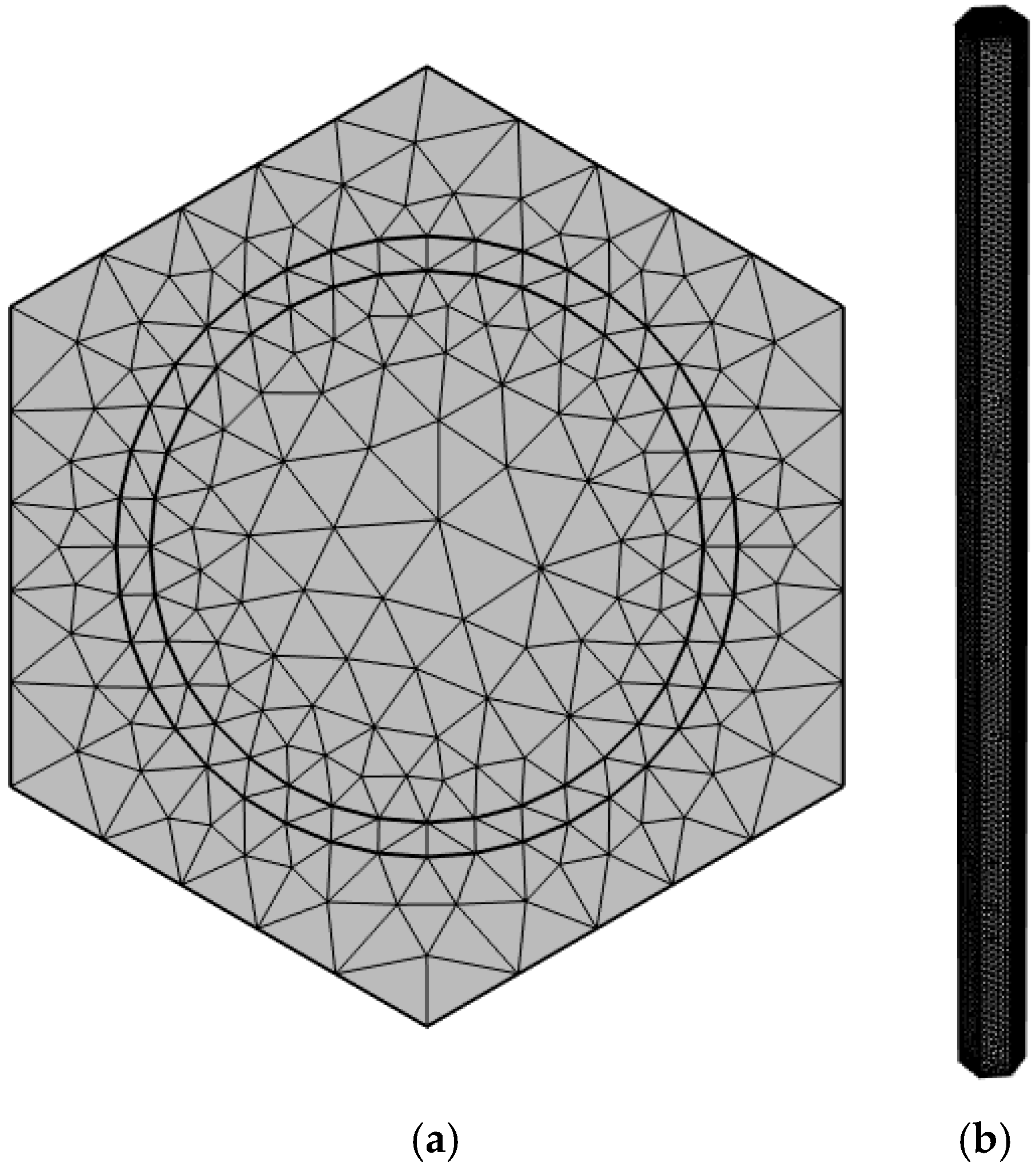
10.8	163
7.9	119

). The initial step in the solution process involves breaking down the geometry into smaller elements, a procedure known as meshing. After that, the partial differential equations (PDEs) are mapped onto this mesh. Free triangular fine mesh was used for simulations and presented in Figure 3. The reason for using triangular elements is that they can conform more easily to complex geometries, such as curved boundaries, fuel rods, cladding layers, and coolant channels. Therefore, triangular meshes adapt better than quadrilateral meshes. However, a normal mesh size was used in all our calculations as we were not able to perform simulations with a finer mesh due to limited computational resources. The authors in the referenced work demonstrated that changing the mesh size can affect the final results, with finer meshes generally producing higher output values [18].

(Th, ²³³U)O₂ was selected as the fuel, and its relevant physical properties were taken from the literature. COMSOL multiphysics can integrate heat transfer, fluid dynamics, and solid mechanics physics into a single model. This multiphysics coupling offers the most faithful representation of real-world behavior, requiring far fewer simplifying assumptions than typical analytical approaches. Three physics modules are used.

2.1. Heat Transfer in Solids

The heat generation PDE is addressed with the FEM. Since thermal power is used for the heating cross-surface of the core, the transient Fourier heat conduction equation is solved to find the spatial distribution of temperature. The PDE is then discretized over the mesh, and solving it provides the temperature distribution within the fuel, cladding, and coolant. Except the top, bottom, and cross surfaces, all other boundaries are assumed to be thermally insulated.

For the thermal properties of fuel [30] and cladding materials [31], the following expressions were used:

Specific heat capacity of (Th, ²³³U)O₂:

$$C_p=239.9+8.512\times {10}^{-5}T-5.754\times {10}^{-8}{T}^2+1.528 \times {10}^{-11}{T}^3\left[{\displaystyle \frac{\mathrm{J}}{\mathrm{mole}\mathrm{K}}}\right]$$

(1)

Thermal conductivity of (Th, ²³³U)O₂:

$$k=14.242-0.022T+1.764\times {10}^{-5}{T}^2-6.380\times {10}^{-9}{T}^3+8.038\times {10}^{-13}{T}^4\left[\mathrm{W}/\mathrm{m}\mathrm{K}\right]$$

(2)

Density of (Th, ²³³U)O₂:

$$\rho =9326-0.0004\mathrm{T}+2.54\times {10}^{-7}{T}^2-7.897\times {10}^{-11}{T}^3\left[\mathrm{kg}/{\mathrm{m}}^3\right]$$

(3)

Specific heat capacity of zircalloy-4:

$$C_p=7.1\cdot {10}^{-2}+1.7\cdot {10}^{-5}\cdot T-0.89\cdot {10}^{-3}\cdot T^2 \left[{\displaystyle \frac{\mathrm{cal}}{\mathrm{g}}}\cdot \mathrm{K}\right]$$

(4)

Thermal conductivity of zircalloy-4:

$$0.11804+0.00012·T-4.33441·{10}^{-8}·T^2+5.90277\times {10}^{-11}·T^3\left[\mathrm{W}/{\mathrm{cm}}^{°}\mathrm{C}\right]$$

(5)

Density of zircalloy-4:

$$\rho =\mathrm{10,950}-0.35·\mathrm{T}-1.2·{10}^{-4}\cdot T^2\left[\mathrm{kg}/{\mathrm{m}}^3\right]$$

(6)

2.2. Fluid Dynamics

The Navier–Stokes PDE for momentum and mass conservation are solved, yielding the pressure drop of the coolant along the axial (z) direction and the corresponding velocity field. When this turbulent flow (k–ω) model is coupled with the heat transfer physics, two key outputs emerge: (1) The convective heat-transfer coefficient, h, which depends on the coolant velocity, the channel geometry (velocity-independent), and the temperature-dependent coolant properties. (2) The axial pressure drop obtained from the Navier–Stokes solution. Combining this pressure drop with the temperature profile and local heat flux from the heat generation equation makes it possible to evaluate the coolant’s distance from nucleate boiling conditions at any location along the z-axis. The water inlet and outlet boundaries are the top and bottom surfaces, respectively.

2.3. Solid Mechanics

Within the solid mechanics interface, the model solves the governing elasticity equations (analogous to Navier–Stokes for solids) to determine the thermal-induced deformation, displacement magnitude, and strain in the fuel and cladding, fully coupled to the heat transfer physics. Top and bottom boundaries are fixed to reflect the physical constraints imposed by the reactor’s structural support system.

For mechanical properties, the following thermal expansion expressions for fuel [32] and cladding materials [30] were used:

$$\begin{gathered} a_{fuel}=5.416\times {10}^{-6}+3.47\times {10}^{-9}T+3.0107\times {10}^{-15}{T}^2-1.2212\times {10}^{-15}{T}^3+4.181\times {10}^{-19}{T}^4\left[1/\mathrm{K}\right] \\ {a}_{clad}=\left(5.22+1.82\times {10}^{-3}T\right)\times {10}^{-6}\left[1/\mathrm{K}\right] \end{gathered}$$

(7)

Young’s Modulus expressions for fuel and cladding materials [30]:

$$\begin{gathered} E_{fuel}=259.87\times {10}^9\times (1-P^2)\left[\mathrm{Pa}\right] \\ \mathrm{P}\mathrm{is}\mathrm{the}\mathrm{porosity} \\ {E}_{clad}=9.21\times {10}^{10}-4.05\times {10}^7\times T\left[\mathrm{Pa}\right] \end{gathered}$$

(8)

The effects of burn-up, plutonium content, pellet cracking, swelling, oxygen-to-metal ratio, and gaseous fission product release on the thermal properties of the fuel are neglected. It is known that elementary particle irradiation affects the mechanical and structural properties of materials [33,34,35]. In this work, irradiation effects are also neglected due to the lack of available data in the literature.

This safety assessment multiphysics COMSOL model, which employs temperature-dependent polynomial expressions for a heavy water reactor fueled with thorium, was built upon previous work on the Comsol multiphysics safety assessment of pressurized water reactors using uranium fuel [36]. The main differences arise from the characteristics of the reactor types—specifically, the fuel and cladding materials, geometric configurations, and operating conditions. Furthermore, the authors developed a similar COMSOL multiphysics model for a pressurized water reactor to demonstrate the feasibility of replacing uranium fuel with thorium [30]. Following a similar motivation, in this work, we aimed to provide a safety assessment for a heavy water reactor when thorium is used instead of uranium. To the best of our knowledge, there are no sources in the literature that present a multiphysics-based safety assessment analysis of CANDU reactors using COMSOL. Furthermore, while the previous model considered only steady-state conditions for a pressurized water reactor, our analysis is performed under transient conditions. A key limitation of this study is the short simulation duration (up to 3 s), which was constrained by the available computational resources.

3. Results and Discussion

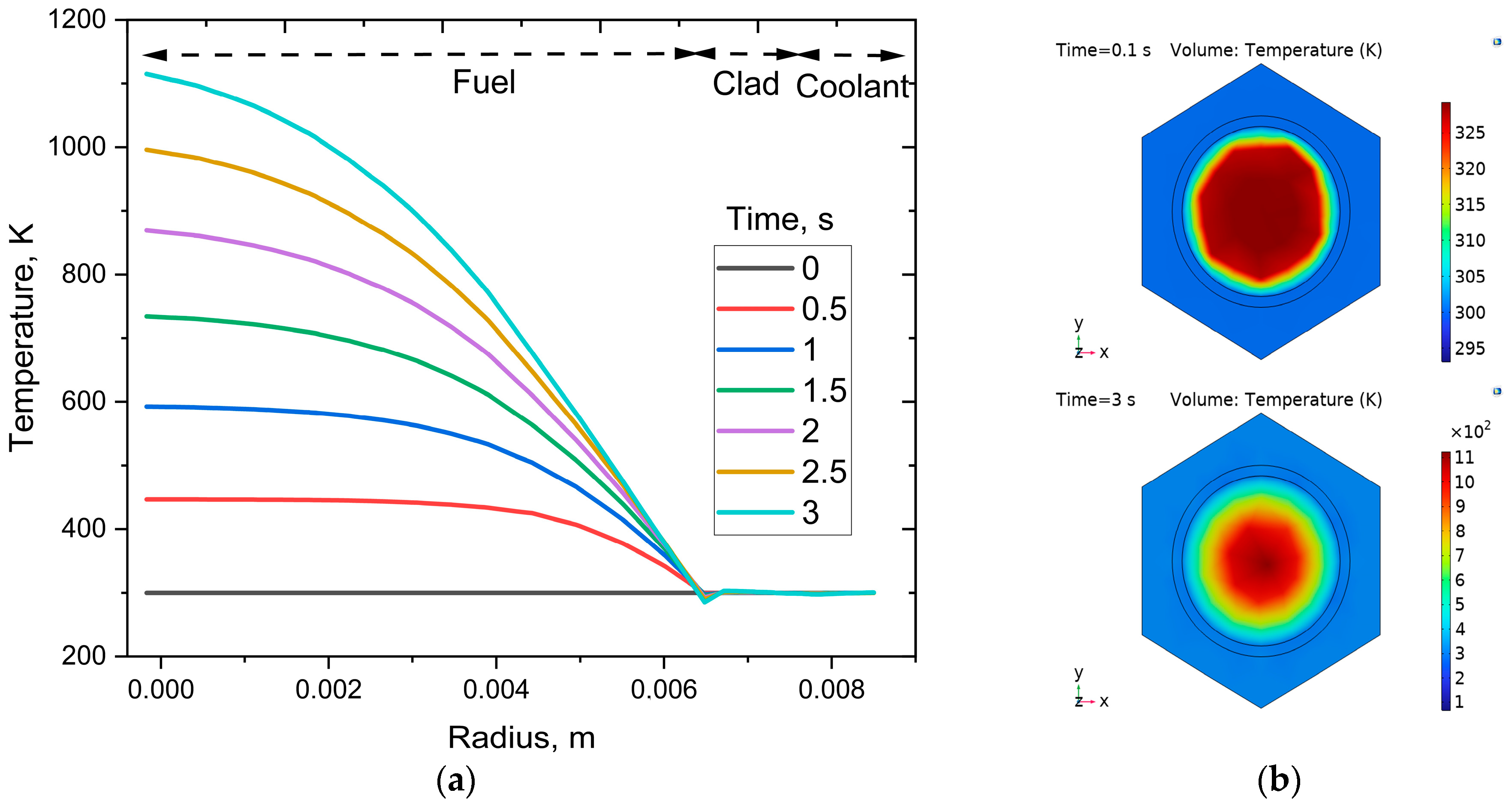
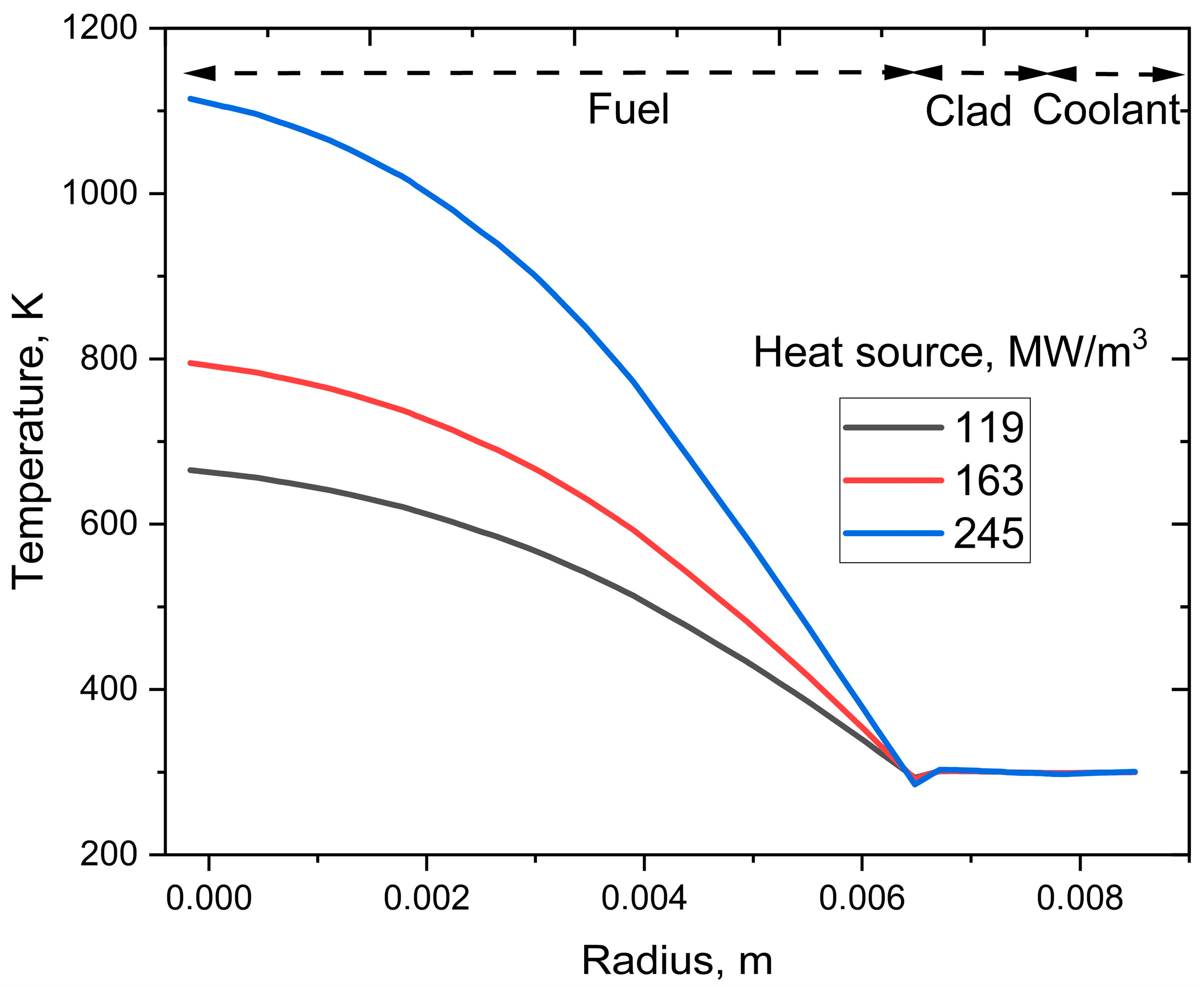
To ensure safe reactor operation, the fuel’s centerline temperature must remain below its melting point, and its average temperature must stay under 1400 °C [37]. The spatial distribution of temperature after application of the maximum heat source for different times (from 0 to 3 s) is shown in Figure 4a. When the heat is transferred from the inner surface of the fuel material to its outer surface, the temperature changes parabolically. The temperature profile along the y–x direction is presented in Figure 4b. As evident from the figure, the reactor core exposed to a heat source for a longer period attains a higher temperature than when the exposure time is shorter. A similar temperature increase in the fuel and cladding materials as a function of time was also observed in the coupled neutronic, thermo-elastic, and fluid dynamics time-dependent model for the single-channel transient analysis of a Lead Fast Reactor [13].

Figure 5 demonstrates the temperature values at 3 s after applying the maximum, median, and minimum heat sources. Overall, the temperature decreases radially from the center of the fuel rod to the coolant boundary. The centerline and average fuel temperatures are below the safety limit. A similar radial temperature distribution in the fuel rod, with a further decrease in the cladding, was observed in the thermo-mechanical analysis of a heat pipe-cooled space reactor [15].

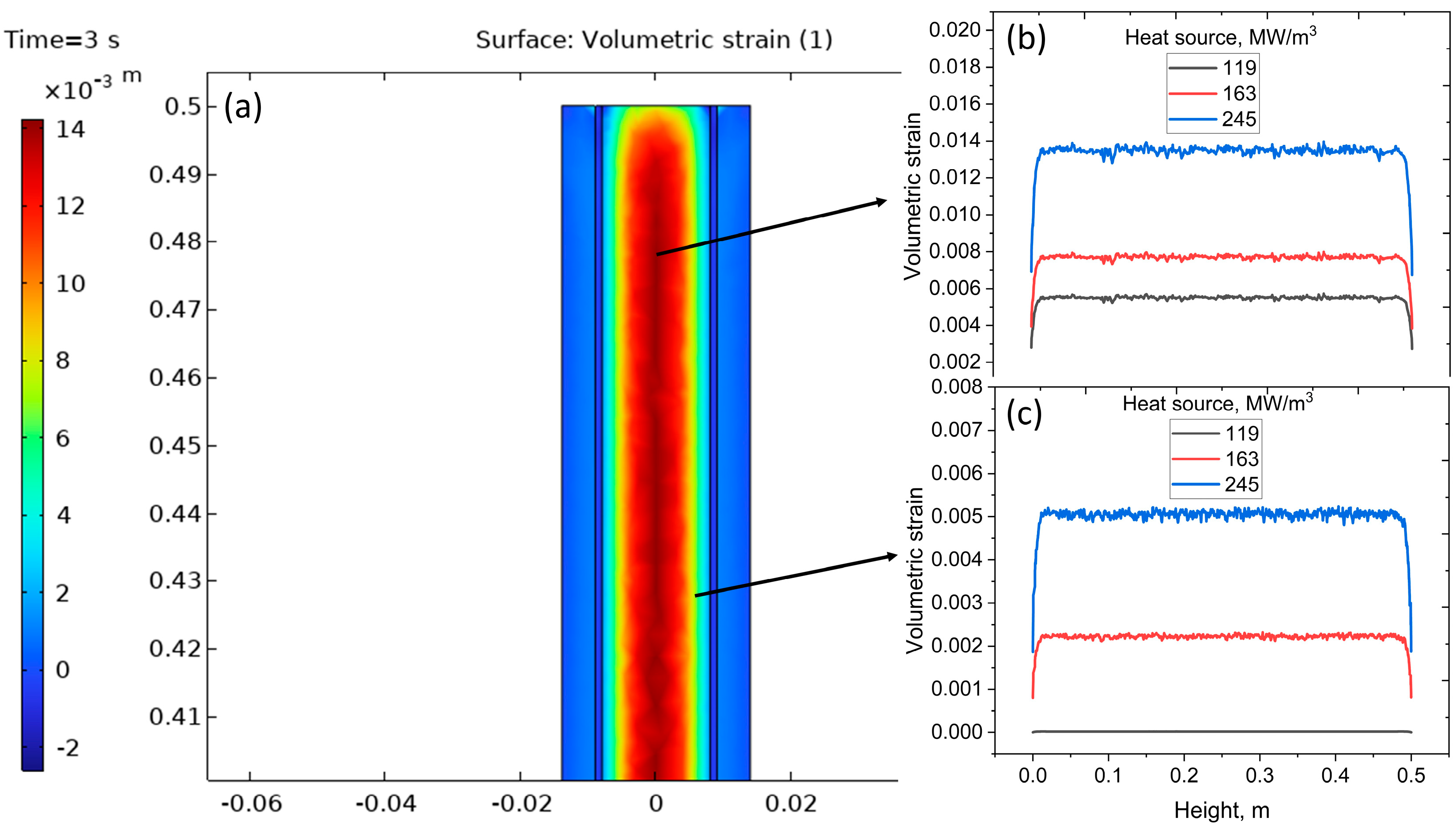
Figure 6 shows the maximum volumetric strain for the fuel material in the axial direction. The 2D strain map shows that after 3 s of heating with a volumetric source of 245 MW m⁻³, there is a characteristic high-strain core surrounded by a low-strain rim (Figure 6a). Axial line profiles (Figure 6b,c) taken through the pellet mid-radius and at the fuel–cladding interface confirm that the strain is remarkably uniform along the central ~0.5 m rod, reflecting the nearly homogeneous internal power distribution. Peak volumetric strain at the center rises from 0.006 to 0.014, respectively, increasing almost linearly with heat generation. Only near the pellet end faces does the strain decrease slightly, a result of end-face mechanical constraints and local heat flux gradients. An increased volumetric strain in the fuel compared to the cladding material was also observed in the literature [36].

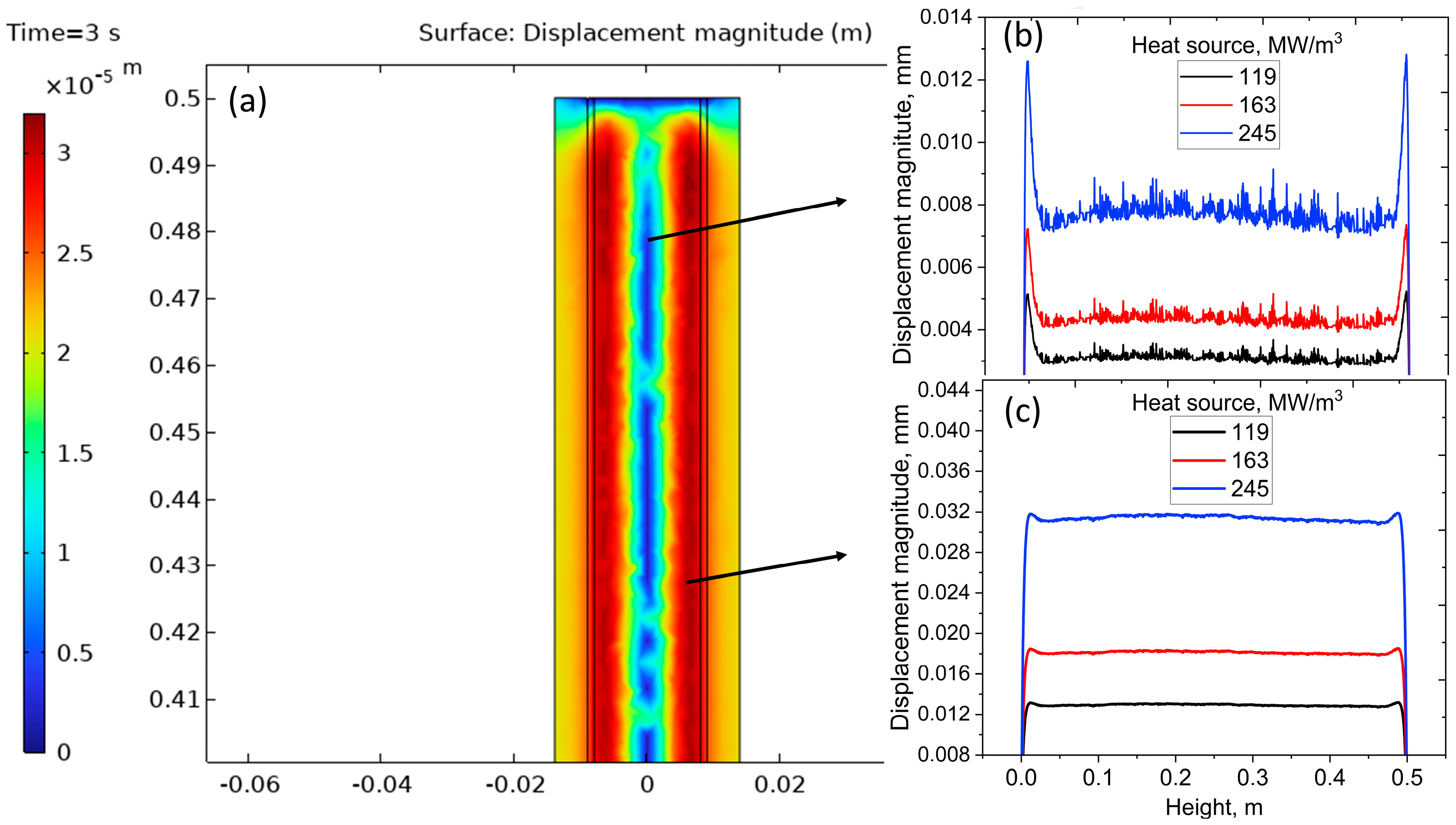
The two-dimensional map of total displacement shows minimal expansion in the central core (Figure 7a), where the cladding constrains radial motion, and maximum displacement along the outer surface where thermal expansion is less restricted. 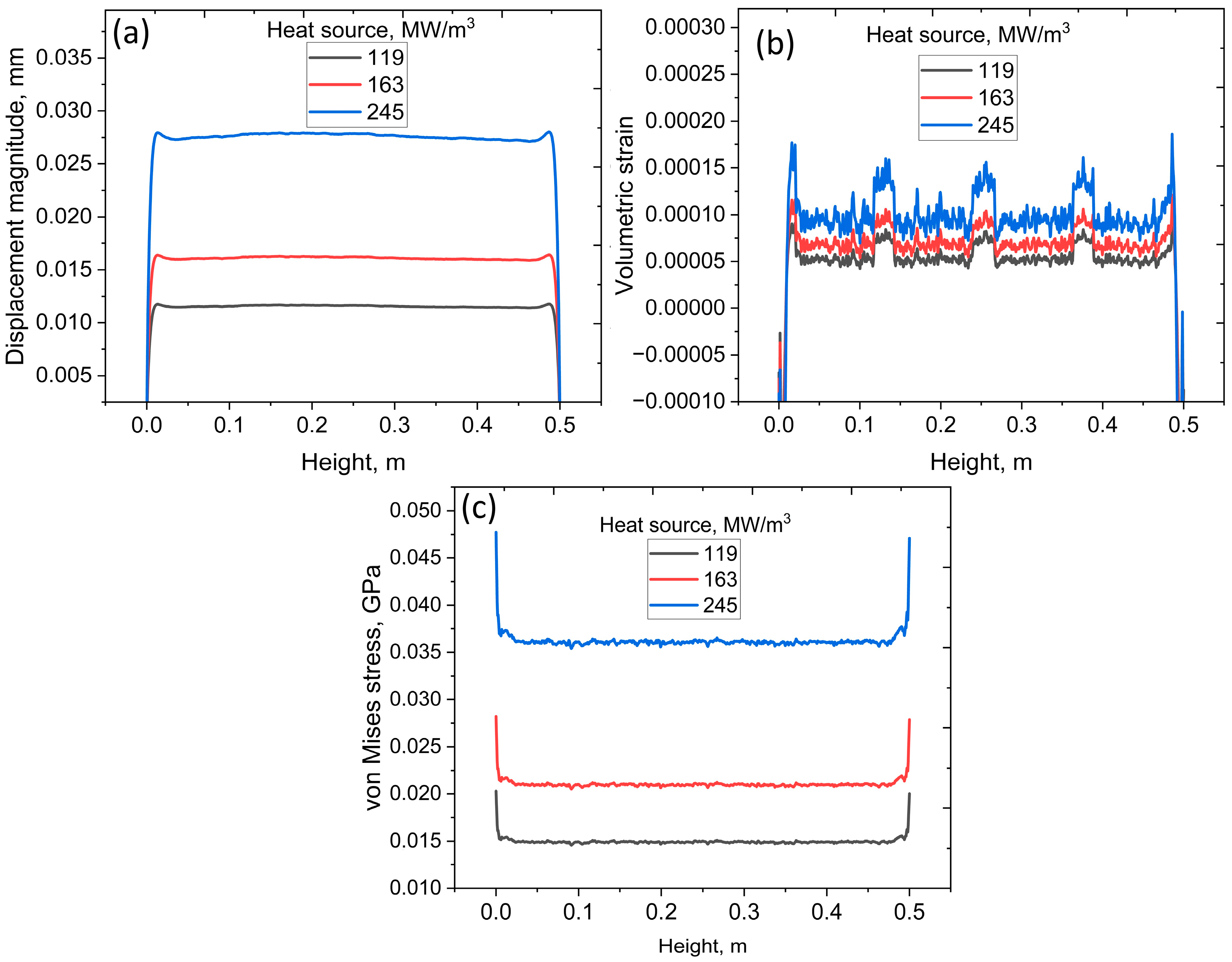Profiles extracted across the diameter (Figure 7b,c) confirm that surface displacement increases systematically with the applied heat source—rising from ~0.004 mm at 119 MW m⁻³ to ~0.012 mm at 245 MW m⁻³—while the center remains comparatively immobile. Axial centerline profiles demonstrate nearly uniform elongation along the heated length, but with magnitudes that also scale with heat source, from ~0.015 mm to ~0.04 mm. The displacement profile suggests non-uniform deformation along the radial length, which is influenced by local thermal and mechanical loading distributions. A similar non-uniform radial deformation pattern was observed by Mohsen et al. [38]. The displacement magnitudes remain within mechanical safety limits, providing critical input for assessing fuel–cladding mechanical interaction and ensuring structural integrity under elevated reactor power conditions.

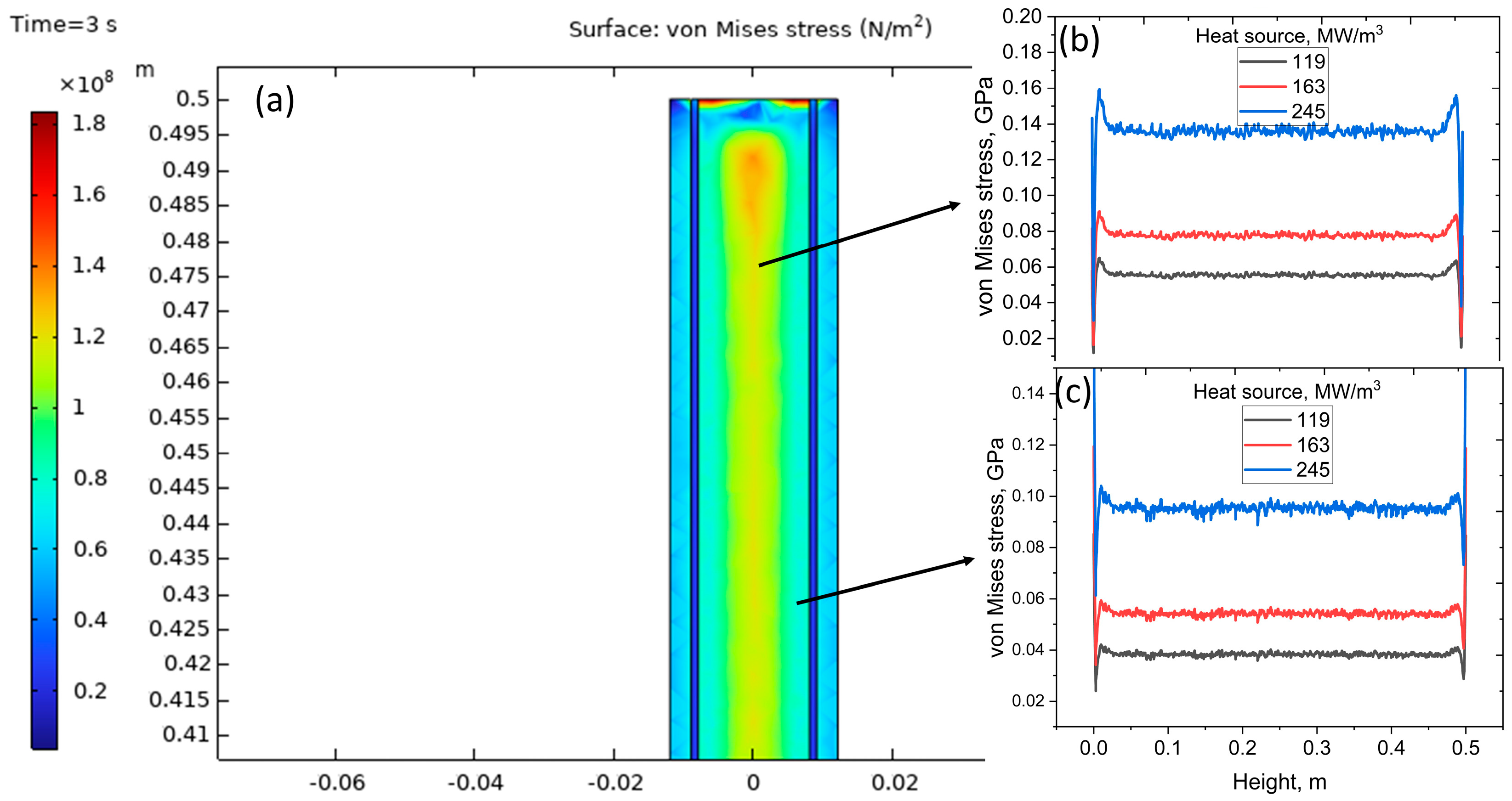
At t = 3 s the fuel rod exhibits an annular von Mises stress distribution with maxima at the outer surface and near-uniform stress along the active height (Figure 8a). Increasing volumetric heat generation from 119 to 245 MW m⁻³ raises centerline stress from ~0.06 to ~0.15 GPa (Figure 8b) and outer surface stress from ~0.04 to ~0.1 GPa (Figure 8c). These results confirm that differential thermal expansion between the hot core and cooler cladding drives the dominant mechanical loading. The stresses remain within structural safety margins but provide critical input for evaluating fuel–cladding mechanical interaction and long-term integrity of the reactor core under high-power operation.

Figure 9 shows the thermo-mechanical simulation results of the cladding material, where higher internal heat generation (119 → 163 → 245 MW m⁻³) causes the cladding to expand almost uniformly along its 0.5 m length while remaining safely elastic. Axial displacement grows steadily from about 0.012 mm to 0.03 mm with increasing heat source, with only small end-effects. However, average strain stays close to zero (≈10⁻⁴), rising slightly with power and showing minor local oscillations, confirming gentle, homogeneous volumetric growth. Mean stress rises from roughly 0.015 GPa to 0.035–0.04 GPa, with small peaks near the ends, remaining well below the yield strength of typical zirconium alloys. These stress results are very close to the von Mises stress values reported for cladding materials in pressurized water reactor with uranium fuel [36].

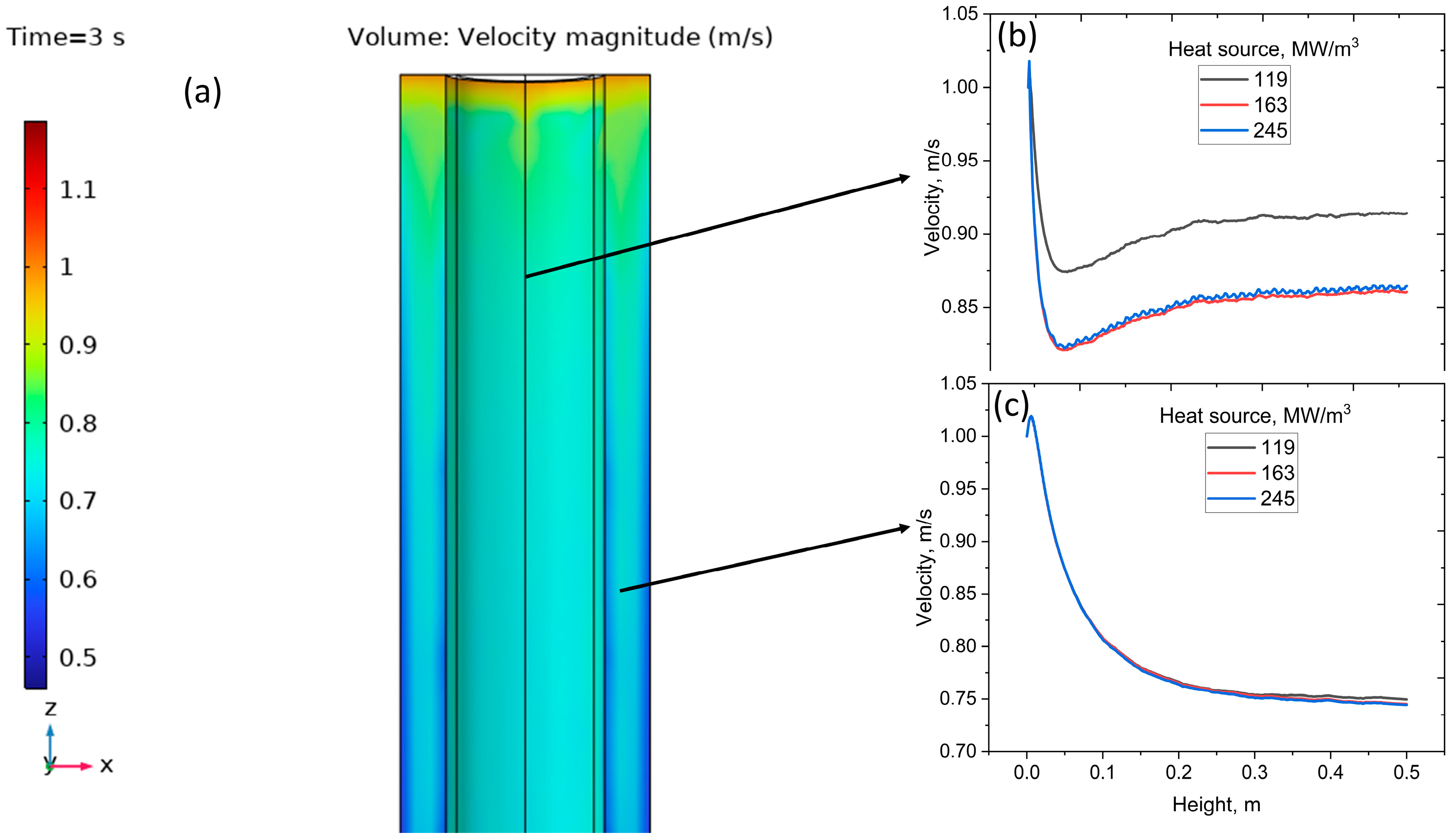
Changes in the velocity profile are evident in Figure 10; over 3 s of operation, the coolant maintains a stable upward flow through the cladding channel (Figure 10a). Surface velocities fall from ~1 m s⁻¹ at the inlet to ~0.85 m s⁻¹ mid-height (Figure 10b), while centerline velocities decrease smoothly to ~0.75 m s⁻¹ at the outlet (Figure 10c). Increasing the internal heat source from 119 to 245 MW m⁻³ produces only slight reductions in surface velocity and negligible changes along the centerline. However, no change in pressure is observed over the 3 s period, even with the increase in heat sources. These results confirm that the hydrodynamic field remains stable and well within design limits, ensuring reliable convective heat removal under the investigated power densities.

4. Conclusions

Thermo-mechanical and hydrodynamic simulations of a thorium-based fuel rod subjected to transient volumetric heating (119 → 245 MW m⁻³ over 3 s) reveal stable structural and coolant responses under elevated power densities. The fuel experiences a characteristic high-strain core surrounded by a low-strain rim, with centerline volumetric strain increasing nearly linearly from 0.006 to 0.014 while remaining axially uniform along the heated 0.5 m segment. Total displacement grows from ~0.004 mm to ~0.012 mm at the surface and from ~0.015 mm to ~0.04 mm along the axis, confirming that radial constraint by the cladding limits central motion. Mechanical loading is dominated by differential thermal expansion, producing annular von Mises stress fields that rise from 0.06 to 0.15 GPa at the center and 0.04 to 0.1 GPa at the surface, yet remain comfortably below zirconium alloy yield strengths. The cladding itself expands almost uniformly, with axial displacement increasing from ~0.012 mm to ~0.03 mm, the average strain being near 10⁻⁴, and mean stress limited to 0.035–0.04 GPa, all well within elastic and design margins. Coolant hydrodynamics remain robust throughout the transient. Upward flow is stable, with only small velocity reductions (surface: 1.0 to 0.85 m s⁻¹; centerline: 0.75 m s⁻¹ at outlet). Collectively, these results confirm that the combined fuel–cladding system maintains mechanical integrity and coolant stability under rapid power ramps to at least 245 MW m⁻³, providing critical design data for next-generation heavy water reactors employing thorium-based fuels.

The present work provides a physics-based computational framework to explore temperature, stress, and coolant responses for a thorium-fueled channel, and full confirmation of these findings will require future experimental measurements and dedicated reactor-scale benchmarking.

Future work includes performing additional thermal hydraulics and solid mechanics analyses under steady-state conditions and over longer time periods to examine further temperature increases in the fuel, cladding, and coolant using more powerful computational resources.