Abstract
Pebble Bed Reactors (PBRs) represent a new generation of nuclear reactors. However, modeling TRi-structural ISOtropic (TRISO) fuel particles employed in PBRs presents a unique challenge in comparison to most conventional reactor designs. Rapid generation of different possible fuel particle configurations for Monte-Carlo simulations provides improved insights into the effects of particle distribution irregularities on the neutron economy. Defective pebbles could cause changes in the neutron flux in a nuclear reactor due to increased or decreased moderating effects. Different configurations of particle fuel also impact isotope production within the nuclear reactor. This study simulates several TRISO configurations representing limited capabilities of randomization algorithms, manufacturing defects configurations and/or special pebble design. All predictions are compared to an equivalent homogenized model used as baseline. The results show that the TRISO configuration has a non-negligible impact on the parameters under consideration. To explain these results, the ratio of the thermal flux of each model to the thermal flux of the homogeneous model is calculated. A clear pattern is observed in the data: as irregularities in the moderator medium emerge due to the distribution of TRISO particles, the neutron spectrum softens, leading to higher values of k∞ and better fuel utilization. This dependence of the spectrum on the TRISO configuration is used to explain the pattern observed in the depletion calculation. The results open the possibility of optimizing the TRISO configuration in manufactured pebbles for fuel utilization and safeguards. Future work should focus on full core simulations to determine the extent of these findings.
1. Introduction
Pebble Bed Reactors (PBRs) are a type of high-temperature reactor whose fuel and design are compatible with molten salt and gas-cooled reactors, both of which are part of the generation IV systems currently being developed under the U.S. Department of Energy missions [1,2]. The concept of a PBR was first conceived by Dr. Farrington Daniels in 1947 with spheres of graphite embedded with fissile material being placed in a configuration to sustain a nuclear chain reaction with coolant passing around the spheres. However, it was not until 1966 that a prototype reactor was constructed to validate Dr. Daniels’ conception. This prototype reactor, the German Arbeitsgemeinschaft Versuchsreaktor (AVR), operated for 21 years until it was shut down due to operational problems [3]. Since then, there has been renewed interest in PBRs on several occasions. The Pebble Bed Modular Reactor (PBMR) was developed by the South African company of the same name from 1994 to 2009. Based on the AVR, it was modified to support a Brayton closed-cycle gas turbine [4]. While a test reactor was planned, it was never constructed due to safety concerns raised on the AVR in 2008 [5]. Since then, two companies have begun exploring the possibility of fuel in pebble configurations. X-energy, based in Bethesda, Maryland, is continuing development of a high-temperature gas reactor in the same vein as the AVR and the PBMR. Their reactor, the Xe-100, is expected to produce 200 MW thermal power and 80 MW electric, placing it within the small-modular reactor category. The other major candidate for PBRs is Kairos Power, based in Alameda, California [6]. Their reactor represents a break from previous PBRs, as their reactor is cooled by molten salt. It is expected to produce 140 MW electric, noticeably higher than the Xe-100. The Xe-100 and the Kairos KP-FHR use high-assay, low-enriched uranium (HALEU) fuel. While most commercial reactors use fuel enriched to 3–5% 235U, HALEU is enriched past that, with the Xe-100 using 15.5% and KP-FHR using 19.75%. X-energy is currently in the pre-application stage with the Nuclear Regulatory Commission, while Kairos received permission to begin construction on a function reactor in 2023, with completion expected in 2026 [7,8].
The first prototype PBR (i.e., the German AVR) was initially fueled using carbide Bi-structural ISOtropic (BISO) fuel. However, during the last 5 years of its operation, TRi-structural ISOtropic (TRISO) fuel was used. TRISO fuel is a nuclear fuel composed of tiny (~1 mm in diameter) particles of fissile materials, most frequently uranium, coated in layers of cladding materials that are usually composed of pyrocarbon and silicon carbide, as shown in Figure 1. Thousands of these TRISO particles are then placed into a larger pebble, with the space between and around them being filled with graphite [2]. The considerable amount of layering between the fissile fuel and the outside of each pebble is one of the primary benefits of using TRISO fuel over traditional oxide fuel pellets. The presence of pyrocarbon and silicon carbide keeps fission products contained, preventing them from leaking into the coolant. The other considerable advantage over traditional fuel is its high durability in the face of high pressures and temperatures. While the Zircaloy rods used in pressurized water reactors (PWRs) can only withstand temperatures up to 647 K (374 °C), TRISO fuel is designed to survive as high as 1800 °C [9]. It also resists corrosion and chemical degradation, ensuring long-term stability. These attributes collectively position TRISO fuel as the most viable and robust fuel form for the inherently dynamic and high-temperature environment of modern Pebble Bed Reactors. An example of an Xe-100 fuel pebble and TRISO fuel particle can be seen in Figure 1, with the material compositions shown in Table 1 and Table 2.

Figure 1.
Fuel pebble for the Xe-100 reactor illustrating the layers in the TRISO fuel particle [10].

Table 1.
Materials and configurations of the TRISO fuel particles in the Xe-100 reactor [11].

Table 2.
Detailed UCO fuel kernel specifications [1,11].
From a computational perspective, the high level of complexity in the geometries of both the TRISO fuel particle and fuel element (e.g., the fuel pebble) in PBRs poses great challenges for the modeling and simulation of such reactors. Previous work has explored the effect of randomly packed pebble beds within the reactor, as well as the effect of randomly distributing the particles throughout the pebble, although such prior studies primarily focused on molten-salt-cooled reactors [12,13], rather than the high-temperature-gas-cooled reactors these pebbles are intended for in this study. Some Monte-Carlo codes, such as Serpent 2 [14], can create randomly packed pebbles through the particle disperser routine [15]. The choice to use MCNP6.2 in this work was driven primarily by institutional access and prior experience. This research builds on this previous work and endeavors to simplify the process of creating complex input files for radiation transport codes, particularly MCNP6.2 [16].
Pebble Bed Reactors present a unique challenge in modeling and measuring burnup due to the moving fuel causing variations in energy-dependent flux exposure and overall burnup. Determination of the ideal model for burnup testing is an important step in this process. Previous work, which usually involved modeling entire reactor cores, has examined the effect of different positions within the reactor [17]. The pebbles were modeled as layers of body-centered cubic lattices, with a corresponding packing factor of 61%. While this is more accurate for modeling whole reactors, there is no significant difference between a body-centered cubic model and simple cubic pebble model for either burnup or k-eigenvalue calculations when applied to a smaller scale. Other studies showed that the regular and random arrangements of the TRISO particles do not have significant impact on criticality when simulated at core level [18,19,20].
Pebble Bed Reactors, such as the Xe-100, are also designed to allow for online refueling, which allows for superior capacity factors when compared to traditional PWRs, which must shut down for extended periods every 12–18 months to refuel. However, the higher enrichments and online refueling make PBRs more attractive to potential proliferators of both fresh fuel and pebbles that have been sent through the reactor and still have relatively low burnup. MCNP6.2 can be used for depletion modeling; however, it encounters the same underlying challenge observed in k-eigenvalue calculations, namely the uncertainty associated with the stochastic distribution of TRISO particles within the fuel matrix. This positional variability directly influences isotopic evolution and must be rigorously characterized to ensure accurate burnup predictions.
The objective of this study is to systematically evaluate how different TRISO particle distributions within a single fuel pebble impact key neutronic and depletion parameters, including multiplication factor, neutron spectrum, and actinide evolution. These configurations were selected to represent a range of possible physical realities such as manufacturing defects, design choices, or limitations in modeling tools. In doing so, this work aims to (1) quantify the influence of spatial heterogeneity within the pebble on reactivity and fuel utilization, and (2) assess whether traditional homogenized models sufficiently capture this behavior. The study also explores the potential implications for safeguards and reactor performance. The findings provide insight into when detailed spatial modeling is necessary and where simplifications may be acceptable. The remainder of this paper is organized as follows: Section 2 introduces the modeled TRISO configurations, Section 3 presents neutronic analysis, Section 4 discusses depletion results, and Section 5 summarizes the key conclusions and implications.
2. Pebble Models with Different TRISO Definitive Locations
Modeling pebbles and TRISO particles in MCNP for both k-eigenvalue and burnup calculations present several challenges, which have several possible solutions. For example, pebbles could be modeled homogeneously, with the fuel region of the pebble being composed of a mixture of materials corresponding to a specific number of TRISO particles and graphite media. Alternatively, the particles could be discrete individual particles with their corresponding layers. This is generally accepted as more accurate, as it is closer to reality. However, these too present challenges in modeling reality. Placing TRISOs into a lattice is straightforward in MCNP but is not representative of real manufactured pebbles. The position of the TRISOs in a real pebble will, to some degree, be randomly distributed within the fueled region, at least for some pebbles currently in development. While the pebbles developed by X-energy contain randomly distributed particles, the pebbles developed by Kairos have a low-density graphite core with the fuel particles distributed as a spherical shell around the core. A decent beginning step is a simple even distribution, heterogeneous pebble, with the TRISOs placed in a lattice and distributed within the pebble. It is also important to consider the possibility of pebbles that were incorrectly manufactured. The position of the TRISOs could have a dramatic effect on the neutron flux and fission rate, and as such, the possibility of TRISOs being concentrated in some areas but missing in others is of concern. The basis of the pebbles in this work is the TRISO-X pebble intended for the Xe-100 reactor. They are 6 cm in diameter, with a 5 cm diameter fuel region, creating a 0.5 cm thick non-fuel region in the periphery. TRISO fuel kernels are enriched to 15.5 wt.% 235U, with a target number of 19,000 particles. They are placed in a 6 × 6 × 6 cm3 cube, with the space not occupied by the pebble taken up by helium.
2.1. Even Model
The heterogeneous, evenly distributed pebble was developed through a geometric “for”-loop in Python3.12. This model used a 35 × 35 × 35 lattice to place TRISO particles throughout the pebble. The particles are packed in simple cubic (SC) configuration. The program would cycle through z-axis levels, using x and y values on that level to determine the position of a prospective particle. This position would then be used in the Pythagorean theorem to test the distance from the edge of the pebble. This allowed for the generation of particles without being cut along the edge of the pebble by limiting particle generation to within the fuel region of the pebble. This process was completed in ~20 s using a typical personal computer, allowing for rapid creation of an MCNP lattice. This did have several drawbacks, however. The number of particles was not precisely 19,000, as a real-life pebble would aim to contain. Still, at 18,949, it was extremely close. The limits of programmed geometry and the dimensions of the pebble and particle limited the number of particles to only approximating realistic goals. Given the constraint of the pebble’s constant diameter, the goal of 19,000 particles could only be approximated with a fixed lattice. However, it did provide the added benefit of being easily edited and much faster than manually producing lattices, although manual lattices have been used in the past in a similar manner [1]. For clarity, this model, shown in Figure 2, is referred to as the “Even” pebble model. Note that the teal region is graphite and the purple part represents the helium cube.

Figure 2.
Cross-sectional view of the Even lattice distribution pebble.
2.2. Secondary Models
Once the Even model was created, modifications were made to explore other possible distributions of TRISO particles within a pebble. Each model is a derivation of the original Even model, created by modifying the original Python script. Among the derivative models included the “Iris” and “Pupil” models. These models have all the TRISO particles either lining the edge of the pebble or concentrated in the center of the pebble. The Iris model mimics the pebbles being developed by Kairos, whereas the Pupil model may represent potentially defective pebbles.
Using the same method from the Even model, the radius restriction was changed for these two models. For the Iris model, the particles were limited to generating between two radii of the pebbles, forming a spherical shell of TRISO particles. For the Pupil model, they were limited to a smaller radius inside the pebble. For data consistency, the number of particles within these models were kept the same as the Even model, that is, 18,949 TRISO particles. This required several steps. First, it required a shrinking of the lattice width. The distance between particles needed to be reduced to allow for more particles within a smaller volume. However, there was no geometry that allowed for the generation of precisely the same number of particles. This led to the necessity of the manual removal of several particles from the input files. Related to the Iris and Pupil versions was the Bottom version, in which all the particles are placed at the bottom of the pebble. This model was created by restricting the generation of particles to the lowest z-levels of the lattice. Again, this version did not contain the exact number of particles upon creation, and manual elimination of a few particles was required. This model represents another possible incorrectly manufactured pebble, with all the TRISOs accidentally placed near the bottom. The geometries of Pupil, Iris, and Bottom models are visualized in Figure 3.
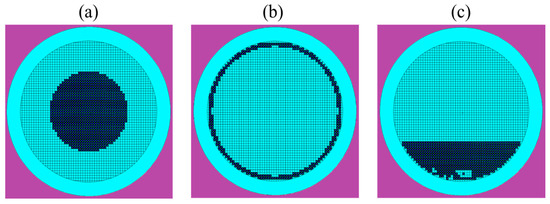
Figure 3.
Cross-sectional view of the (a) Pupil distribution, (b) Iris distribution, and (c) Bottom distribution.
2.3. Semi-Random Model
The next model created was the Semi-Random version. This version uses the same lattice size as the Pupil, Iris, and Bottom pebbles, but all lattice spots were filled with a particle. This creates approximately five times as many particles as desired within the pebble. Then, the Python script removed approximately 80% of the particles, resulting in the same number of particles as the other models. This would not result in a purely randomized particle distribution due to the particles still being in a lattice structure. Previous work was performed on randomly distributed particles [12]; however, this variation is different in its lack of perfect randomness, with the particles still placed in an ordered lattice. The Semi-Random pebble model is most representative of an ideal pebble while retaining definitive particle locations. It is important to note that a fully random, non-lattice-based packing could introduce additional spatial variability that may influence depletion behavior. A cut-in view of the Semi-Random pebble model is shown in Figure 4.

Figure 4.
Cross-sectional view of the Semi-Random distribution pebble.
2.4. URAN Model and Variations
MCNP6.2 possesses a stochastic geometry function, the URAN card. The URAN card provides limited stochastic geometry modeling in an MCNP6.2 lattice, allowing for limited randomness in particle distribution. During an MCNP6.2 simulation that uses the URAN card, there is a geometric transformation whenever a neutron enters a lattice element that is flagged as stochastic [21]. The URAN card takes a universe and 3 user inputs regarding limits on how far a designated universe element can move to determine the extent of the geometric transformation. Those limits are especially important for purposes such as this due to the limitations of the URAN card. URAN is incompatible with the MCNP plotting software Visual Editor [22], meaning that any possible cut or overlapping particles cannot be visually found and fixed before an MCNP6.2 simulation is executed. As such, it is safer to limit the distance a universe element can be moved to be within its singular lattice cube. The URAN card was applied to the Even model, with a varying degree of freedom of movement. To illustrate the effect of the URAN model, one possible TRISO particle placement in a 3-by-3 lattice grid within the pebble after the URAN function is shown in Figure 5. The particles moving slightly off the positions of the Even model in random directions via the URAN card is clearly demonstrated in Figure 5.
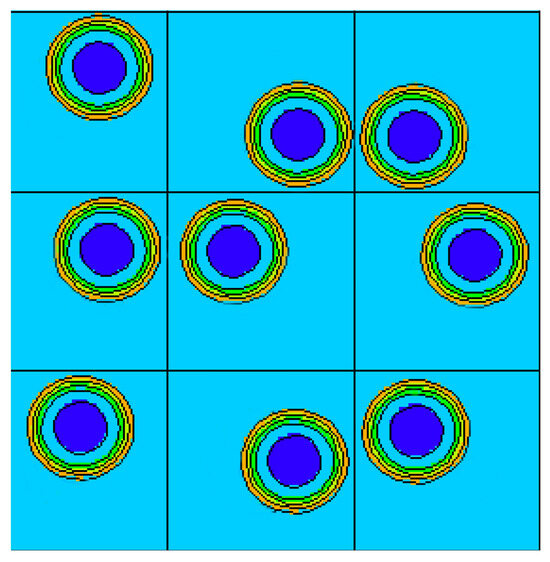
Figure 5.
Randomly moved particles as would be expected using URAN. The different colored shells represent the layers of in TRISO particle, as described in Table 1.
3. Eigenvalue (K-Code) Simulation
All of the pebble models described in Section 2 were placed into a cube of helium with a reflective boundary to represent how the neutronics of a pebble would perform in the center of a PBR. In this regard, only the infinite multiplication factor (i.e., the k∞ value) is produced through these models. All the computational models were developed and simulated via the k-code calculations in MCNP6.2 to determine how the particle distribution would affect the neutronics performance. The ENDF/B VII.1 cross-sections at 1200 K [23] were used for all the calculations. The k-code simulations were executed with 10,000 neutron particles per batch with 80 batches, including 10 inactive batches. The number of simulated particles was selected to ensure that the statistical uncertainty in the k∞ values remained below 50 pcm (1 pcm = 10−5). To establish a reference model for evaluating the effect of TRISO pebble distribution of neutronics behavior, a homogenous model was developed and simulated using the same parameters. In the homogenous model, the fuel region of the pebble was represented as a uniform material conserving the isotopic composition of the heterogeneous models. The results of the eigenvalue simulations are summarized in Table 3.

Table 3.
The k∞ values with one-sigma statistical uncertainties for the different models.
The k∞ values across different models reveal a clear pattern, increasing as TRISO particles become more concentrated within specific regions of the geometry. The homogeneous model yielded the lowest k∞, while the two extreme cases, Pupil and Bottom, resulted in significantly higher values. In contrast, the Even and Semi-Random models produced close k∞ values, likely due to the dispersion of TRISO particles within the same pebble volume, unlike the other heterogeneous models.
In the URAN model, the distribution of TRISO particles is influenced by the degree of freedom, defined as the maximum distance a universe can be randomly displaced. To assess the impact of this degree of freedom on system behavior, three sets of calculations were performed, allowing the universe to move within the entire, half, or quarter of a lattice cell. All results are compared to the homogeneous model.
The results shown in Table 4 show that the k∞ values are intermediate between those of the Even and Semi-Random models. As the degree of freedom decreases, the k∞ converges to the value of the Even model, which is expected. The results also show that even with the TRISO particles are allowed to be displaced freely within the lattice cell, the deviation in the k∞ values from the Even model (zero displacement) remains minimal compared to other models, such as the Semi-Random. This is because the URAN method maintains on average a consistent particle density across the pebble volume. In contrast, the Semi-Random model used a much smaller lattice pitch. Despite having the same number of TRISO particles, this can lead to regions with high particle density and others with low density, which appears to increase k∞. Similar results are reported in Ref. [24] for the HTR fuel rod when comparing the Quasi-random and URAN packing algorithms.

Table 4.
URAN particle freedom of movement comparison in k∞ values.
The dependence of the eigenvalue (k∞) on the model originates from variations in the fuel/moderator configuration, which in turn affect resonance escape probability and consequently alter the neutron spectrum. To investigate the impact of the pebble configuration on the neutron spectrum, neutron energy flux tallies were simulated on all the pebble models using a 252-energy group structure [25]. Figure 6 shows the neutron spectrum for all the Pebble models considered. The spectrum for the homogeneous model is significantly harder than the heterogeneous models. This indicates that the homogeneous model has the lowest resonance escape probability. In uniform material, the probability that a neutron emitted from a fission site would have its next interaction with a fissile nuclide is proportional to the atom fraction of fissile isotopes. This could explain the harder spectrum in the homogenous model, as the higher likelihood of a neutron encountering a fissile nuclide before undergoing sufficient moderation results in reduced thermalization.
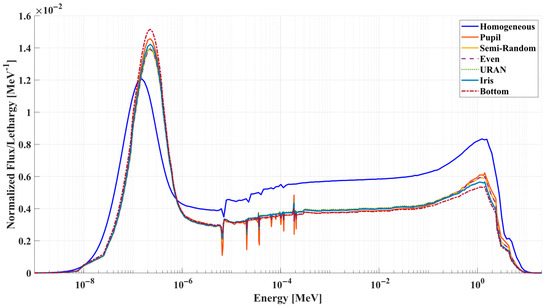
Figure 6.
Neutron energy spectra for various pebble geometries. A softer neutron spectrum, characterized by a higher fraction of thermal neutrons, is observed in geometries with more irregular TRISO distributions.
As the heterogeneity of the model increases, the neutron spectrum becomes softer. As fissile isotopes clustered in specific regions are separated by moderator regions, the probability of a neutron emitted from a fission site having its next interaction with a fissile nuclide decreases. This would result in better thermalization and hence higher k∞. To quantify this effect, the thermal neutron population is calculated for each model. Then, the ratio of the thermal population for a heterogeneous model to the thermal population for the homogenous model is calculated as a resonance escape probability metric. The values listed in Table 5 are ordered in ascending order of the resonance escape probability metric. The pattern is evident: as TRISO particles become more clustered, resulting in a higher local packing factor, resonance escape probability improves. This clustering within specific regions of the pebble enhances neutron moderation by increasing the likelihood that a fission neutron will interact with the moderator before encountering a fissile isotope. Interestingly, the defined resonance escape probability metric can be seen as an indirect indicator of the Dancoff factor, defined as the probability for a neutron that leaves the fuel zone of a pebble to enter another fuel zone without any interaction in between [26].

Table 5.
The ratio of the thermal population for the heterogeneous models to the thermal population of the homogenous model.
The analysis presented confirms that the distribution of TRISO particles within a pebble has a significant impact on key neutronic parameters. These findings carry important implications for pebble fabrication and pebble simulation. First, it is important to use a model that accurately represents the spatial distribution of TRISO particles in a manufactured pebble. A representative distribution ensures that simulation models closely reflect real-world fuel behavior, leading to more accurate predictions. Second, deviations from the intended TRISO particle arrangement can lead to notable differences in neutron moderation. Improperly manufactured pebbles may exhibit behaviors that deviate from the expected design, potentially affecting reactor safety, fuel utilization, and operational efficiency.
However, these variations could potentially disappear in a full reactor core model or at least be reduced. The increased opportunity for moderation in the moderator/reflector placed outside of the core, as well as the possibility of leakage, is expected to reduce the overall impact of these variations. Work currently being conducted on an Xe-100 reactor model in OpenMC supports this hypothesis [27,28].
4. Composition Evolution of Various Configurations
4.1. Analysis Approach
As discussed in Section 3, the TRISO particles’ distribution has a significant impact on the neutron energy spectrum, which is expected to impact the evolution of the isotopic inventory due to the energy dependence of cross-sections. To understand the effect of different pebble models under fuel burn conditions, single-pebble burnup simulations were performed in MCNP6.2 using the Even model, the Semi-Random model, and the Full-Cell URAN model, while using the homogenous model as a reference. The k-code parameters applied in this study were 10,000 particles per batch with 40 batches, while the 10 initial batches were discarded in all cases. The pebbles were burned using CINDER, with 97 timesteps that count for a total of 1304 days of burn at full power of 909 W (assuming 200 MW thermal power and ~220,000 pebbles for the reactor). In the coupled MCNP-CINDER workflow, MCNP computes neutron fluxes using continuous-energy Monte-Carlo transport, which are then passed as a multigroup energy structure to CINDER to solve the Bateman equations for transmutation and decay. Using predefined depletion chains and cross-section data, CINDER updates the isotopic composition over each burnup step. These updated compositions are fed back into MCNP, forming an iterative transport–depletion cycle. The targeted maximum burnup was 160,000 MWD/MTU, which is the expected burnup for the Xe-100 reactor [29]. The initial enrichment is 15.5% with 18,949 TRISO particles in each pebble. A single material is used for the UCO kernels, averaging depletion and transmutation across the pebble. Of primary concern are the change in k∞ over time, the reduction in 235U, the production of 239Pu, and the plutonium isotopic composition. To quantify the statistical uncertainty in the depletion results, each heterogeneous model was simulated using three independent MCNP–CINDER runs with different random seeds. The resulting isotopic inventories were averaged, and the standard deviation across runs was computed for key isotopes such as 235U and 239Pu. The maximum observed uncertainty in these inventories was approximately 0.8 mg, which corresponds to a relative uncertainty of less than 0.2% over the full depletion range. Given that the differences in isotopic evolution between heterogeneous models are small, this uncertainty assessment confirms that the trends observed—such as improved fuel utilization or reduced 239Pu buildup in more heterogeneous cases—are statistically meaningful within the resolution of the simulations.
4.2. Impact on the Multiplication Factor (k∞)
As the pebble is modeled as stationary and the burnup is continuous with a single power level for the entirety of the burn, the change in k∞ is representative of the change in fissionable material in the pebble and its usefulness in the reactor. Once a pebble drops below critical (k∞ < 1), it stands to reason that it should be cycled out of the reactor. Due to the equivalent burnup, all three heterogeneous pebble models drop below criticality at approximately the same time, as can be seen in Figure 7.
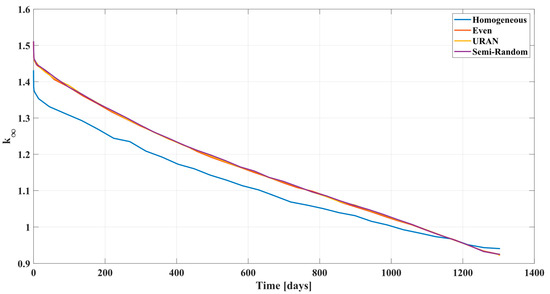
Figure 7.
The change in k∞ with burnup in the different models. Models with more irregular or heterogeneous particle distributions exhibit a slower decline in k∞ relative to the homogeneous model.
The homogeneous model has considerably lower k∞, which dropped below critically after about 1000 days. On the other hand, the heterogeneous models remained super-critical for 1100 days, indicating better fuel utilization with increasing heterogeneity. Heterogeneity refers to the distribution of regions of high local packing factors and regions with low local packing factor. An interesting observation occurs at 1200 days when the k∞ of the homogeneous models becomes higher than other models, indicating significant variations in the fissile inventory as discussed in the following subsection.
When comparing the heterogeneous models, the rate of reactivity drop is very similar, whereas when directly compared to the Even model, both the URAN and Semi-Random models vary only by about 0.5% at most, as shown in Figure 8.
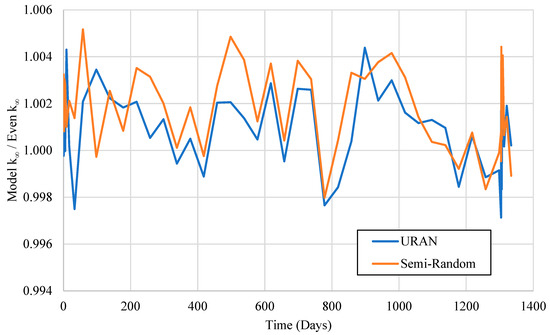
Figure 8.
Ratio of k∞ for the Even model to k∞ of the other models for burnup over time.
The pattern of these curves indicates the randomized models (URAN and Semi-Random) appear to have k∞ values that are statistically greater than the Even model (the ratio is greater than 1.000). However, when comparing the URAN and Semi-Random models to each other, they visually appear to be statistically the same. This implies that randomization has a slight but statistically significant impact on k∞. Also, the method of randomization appears to impact the evolution of k∞, as the more randomized model (Semi-Random model in this case) tends to have slightly higher k∞.
4.3. Actinide Production
Another important factor to consider for burnup are the major actinides that are produced and consumed. The concentration of different actinides at different burnup values is important from both a fuel consumption standpoint as well as a nonproliferation standpoint. In terms of fuel consumption, if sufficient fissionable materials remain in the pebble to be critical, then the pebble is worth reusing. Unfortunately, high levels of fissionable materials can also make the pebbles more attractive for weaponization, with the production of 239Pu being of particular importance [30,31,32,33]. The evolution of 235U and 239Pu inventories, as predicted using various pebble models, is shown in Figure 9.
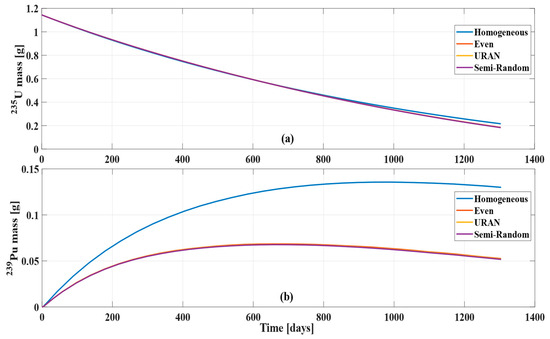
Figure 9.
The evolution of: (a) 235U inventory and (b) 239Pu inventory over time (burnup) for four different TRISO particle distribution models. Models with more heterogeneous distributions tend to exhibit slower depletion of 235U and increased buildup of 239Pu.
The results in Figure 9 show that the three heterogeneous models consume 235U approximately the same rate, whereas the homogeneous model starts to show a slower rate of burning 235U after 800 days. On the other hand, the 239Pu inventory exhibits significant deviation among the models studied. There is a slight deviation in 239Pu content for the three heterogeneous models, visually starting around 300 days (~37,000 MWD/MTU). At 600 days the difference between the Even and Semi-Random models is 1.3% and the difference between URAN and Semi-Random is 0.4%. These differences increase at the end of life (1304 days) to 1.8% and 0.8%, respectively. For the homogeneous model, the 239Pu accumulation is as high as twice that of the heterogeneous models.
An explanation of these trends can be obtained by considering the production and consumption mechanisms of each isotope. 235U is the main fissionable isotope, hence its consumption rate is determined by the fission rate (or equivalently burnup power), which is the same for all models. This explains the similarity in the evolution of 235U inventory among all models. Near the end of the cycle, variations in the 235U inventory start to be noticeable as the contribution of the TRU to the fission becomes significant. The variations in the TRU inventory in each model alters the consumption rate of 235U at the same power generation. The evolution of 239Pu inventory is governed by the production rate through 238U (n, γ) 239U reaction and the consumption rate through 239Pu (n, γ) 240Pu and 239Pu (n, f) reactions. While the 239Pu production rate is expected to be more or less the same among all models, the consumption rate is significantly different due to spectrum variation. To demonstrate this, the energy-dependent cross-section for the two consumption reactions is plotted against the neutron spectrum for the Homogeneous and the Even models. Figure 10 shows that consumption reactions have a peak at about (), which aligns with the thermal peak of the heterogeneous models. As for the Homogeneous model, the thermal peak is smaller and slightly shifted to lower energy, while the 239Pu consumption rate is significantly lower and thus accumulates to higher levels. This conclusion can be extended to all other models; as the model becomes more heterogeneous, the rate of 239Pu accumulation is reduced. The larger fissile inventory for the Homogeneous model explains the larger k∞ at the end of cycle.
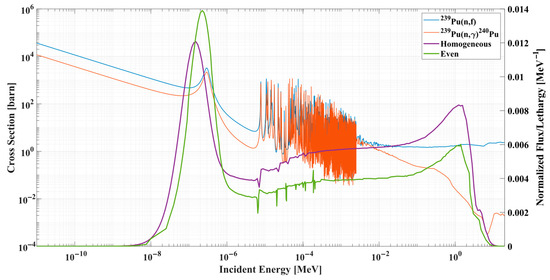
Figure 10.
ENDF/B-VII.1 cross-sections of 239Pu (n, γ) 240Pu and 239Pu (n, f) reactions on the left y-axis, and neutron energy spectrum for the Homogeneous and Even models on the right y-axis.
The analysis of the burnup calculations confirms the previous conclusion for the neutronics analysis. The TRISO particles distribution within the pebble has a non-negligible impact on pebble behavior. Thus, quality control on pebble production and realistic simulations of the pebble configuration are important in ensuring fuel performance under safety, fuel economy, and safeguards considerations.
5. Conclusions
This study investigated the neutronics and depletion behavior of various TRISO particle configurations within fuel pebbles, representative of either manufacturing variation, deliberate design features, or limitations in simulation algorithms. The performance of these configurations including Even, Semi-Random, URAN, Iris, Pupil, and Bottom was benchmarked against a homogenized reference model using MCNP6.2.
The results demonstrate that the internal distribution of TRISO particles significantly affects pebble behavior. Key findings include the following:
Neutronics Sensitivity: Heterogeneous models showed higher k∞ values compared to the homogenized model. Concentration of TRISO particles in localized regions (e.g., Pupil, Bottom) further amplified this effect, softening the neutron spectrum and improving the resonance escape probability.
Burnup Behavior: Models with more irregular TRISO distributions maintained supercriticality longer and exhibited slightly slower 235U depletion. These same models also showed reduced 239Pu accumulation, which may have implications for both fuel utilization and safeguards.
Impact of Randomization Method: The Semi-Random and URAN models displayed subtle differences in reactivity and plutonium buildup, suggesting that the method of generating randomness in simulations can influence results and should be carefully considered.
Practical Implications: The findings of this study carry several practical implications for modeling, fabrication, and future design of pebble fuel. First, single-pebble simulations should avoid oversimplified homogeneous models, especially when assessing reactivity or isotopic evolution, as such models may not capture important spatial effects. Second, manufacturing variability in TRISO particle placement can meaningfully influence fuel behavior; thus, improved quality control or characterization of particle distributions within pebbles could enhance reactor performance and reduce uncertainties in predictive modeling. Finally, while this study does not propose a specific optimization strategy, it demonstrated that neutronics and burnup behavior are sensitive to TRISO distribution suggesting that designing pebbles with tailored moderation characteristics may offer pathways for improving fuel utilization and proliferation resistance.
Future work should focus on whole-core simulations to evaluate whether these localized effects average out or persist at scale. Additionally, incorporating thermal–hydraulic and mechanical behavior in tandem with depletion modeling will be essential to assess whether optimized TRISO distributions are viable from a fuel performance and safety standpoint.
Author Contributions
Conceptualization, Z.W. and B.G.; Methodology, B.I., Z.W. and B.G.; Software, B.I., Z.W. and B.G.; Validation, B.I., M.E., Z.W. and B.G.; Investigation, B.I., Z.W. and B.G.; Writing—original draft, B.I.; Writing—review & editing, M.E., Z.W. and B.G.; Visualization, B.I. and M.E.; Supervision, Z.W. and B.G.; Project administration, Z.W. and B.G.; Funding acquisition, B.G. All authors have read and agreed to the published version of the manuscript.
Funding
This work is performed with the support of the U.S. Department of Energy’s Nuclear Energy University Program (NEUP) with the Award No. DE-NE0009304. The authors acknowledge the College of Engineering at the Virginia Commonwealth University for providing high-performance computing resources that have contributed to the research results reported within this paper.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Helmreich, G.W.; Hunn, J.D.; McMurray, J.W.; Hunt, R.D.; Jolly, B.C.; Trammell, M.P.; Brown, D.R.; Blamer, B.J.; Reif, T.J.; Kim, H.T. Year One Summary of X-energy Pebble Fuel Development at ORNL; ORNL/TM-2017/337; Oak Ridge National Laboratory (ORNL): Oak Ridge, TN, USA, 2017. [Google Scholar]
- Locatelli, G.; Mancini, M.; Todeschini, N. Generation IV nuclear reactors: Current status and future prospects. Energy Policy 2013, 61, 1503–1520. [Google Scholar] [CrossRef]
- Ziermann, E.; Ivens, G. Final Report About Operation of the AVR Experimental Nuclear Power Station (Juel-3448); IAEA: Vienna, Austria, 1997. (In German) [Google Scholar]
- IAEA. Status Report 70—Pebble Bed Modular Reactor (PBMR); IAEA: Vienna, Austria, 2011. [Google Scholar]
- Moormann, R. A Safety Re-Evaluation of the AVR Pebble Bed Reactor Operation and Its Consequences for Future HTR Concepts. In Proceedings of the Fourth International Topical Meeting on High Temperature Reactor Technology, Washington, DC, USA, 28 September–1 October 2008. [Google Scholar]
- Zhao, H.; Fick, L.; Heald, A.; Zhou, Q.; Richesson, S.; Sutton, N.; Haugh, B. Development, Verification, and Validation of an Advanced Systems Code KP-SAM for Kairos Power Fluoride Salt–Cooled High-Temperature Reactor (KP-FHR). Nucl. Sci. Eng. 2023, 197, 813–839. [Google Scholar] [CrossRef]
- Mulder, E.J.; Boyes, W.A. Neutronics characteristics of a 165 MWth Xe-100 reactor. Nucl. Eng. Des. 2020, 357, 110415. [Google Scholar] [CrossRef]
- Satvat, N.; Hernandez, R.; Vitullo, F.; Riley, K.; Fratoni, M.; Haugh, B.; Blandford, E. Hermes Reactor Demonstration, Initial Startup, and Physics Testing. Nucl. Sci. Eng. 2025, 1–11. [Google Scholar] [CrossRef]
- Loza, P.; Staden, M.V. Submittal of Xe-100 Topical Report: TRISO-X Pebble Fuel Qualification Methodology; Revision 2; X-Energy: Rockville, MD, USA, 2021. [Google Scholar]
- X-energy. Advanced TRISO Particle Fuel for Gen 4 Nuclear Reactors. Available online: https://x-energy.com/fuel/triso-x (accessed on 7 March 2024).
- Marshall, D.W.; Maki, J.T.; Demkocwicz, P.A.; Mitchell, T.R.; Sharp, M.T. AGR-5/6/7 Fuel Specification. INL Tech Report; Idaho National Laboratory: Idaho Falls, ID, USA, 2017. [Google Scholar]
- Auwerda, G.J.; Kloosterman, J.L.; Lathouwers, D.; van der Hagen, T.H.J.J. Effects of random pebble distribution on the multiplication factor in HTR pebble bed reactors. Ann. Nucl. Energy 2010, 37, 1056–1066. [Google Scholar] [CrossRef]
- Li, Z.; Cao, L.; Wu, H.; He, Q.; Shen, W. On the improvements in neutronics analysis of the unit cell for the pebble-bed fluoride-salt-cooled high-temperature reactor. Prog. Nucl. Energy 2016, 93, 287–296. [Google Scholar] [CrossRef]
- Leppänen, J.; Valtavirta, V.; Rintala, A.; Tuominen, R. Status of Serpent Monte Carlo code in 2024. EPJ Nucl. Sci. Technol. 2025, 11, 3. [Google Scholar] [CrossRef]
- Rintala, V.; Suikkanen, H.; Leppänen, J.; Rajamäki, R.K. Modeling of realistic pebble bed reactor geometries using the Serpent Monte Carlo code. Ann. Nucl. Energy 2015, 77, 223–230. [Google Scholar] [CrossRef]
- Werner, C.J.; Bull, J.S.; Solomon, C.J.; Brown, F.B.; McKinney, G.W.; Rising, M.E.; Dixon, D.A.; Martz, R.L.; Hughes, H.G.; Cox, L.J.; et al. MCNP6.2 Release Notes; LA-UR-18-20808; Los Alamos National Laboratory: Los Alamos, NM, USA, 2018. [Google Scholar]
- Mulyana, D.; Chirayath, S.S. The impact of refueling schemes on the proliferation resistance of a pebble bed reactor. Ann. Nucl. Energy 2022, 170, 109010. [Google Scholar] [CrossRef]
- Colak, Ü.; Seker, V. Monte Carlo criticality calculations for a pebble bed reactor with MCNP. Nucl. Sci. Eng. 2005, 149, 131–137. [Google Scholar] [CrossRef]
- Kim, H.-C.; Kim, S.H.; Kim, J.K. A new strategy to simulate a random geometry in a pebble-bed core with the Monte Carlo code MCNP. Ann. Nucl. Energy 2011, 38, 1877–1883. [Google Scholar] [CrossRef]
- Abedi, A.; Vosoughi, N. Neutronic simulation of a pebble bed reactor considering its double heterogeneous nature. Nucl. Eng. Des. 2012, 253, 277–284. [Google Scholar] [CrossRef]
- Brown, F.B.; Martin, W.R. Stochastic geometry capability in MCNP5 for the analysis of particle fuel. Ann. Nucl. Energy 2004, 31, 2039–2047. [Google Scholar] [CrossRef]
- Schwarz, R.A. Current Status of the MCNP Visual Editor. In Proceedings of the 2002 Topical on Radiation Protection and Shielding, Santa Fe, NM, USA, 14–18 April 2002. [Google Scholar]
- Conlin, J.L.; Gardiner, S.J.; Parsons, D.K.; Kahler, A.C.; Lee, B.; White, M.C. Release of ENDF/B-VII.1-Based Continuous Energy Neutron Cross Section Data Tables for MCNP; LA-UR-20240 (Report) LA-UR-13-24077 (Presentation); Los Alamos National Laboratory: Los Alamos, NM, USA, 2013. [Google Scholar]
- Kępisty, G.; Stanisz, P.; Cetnar, J. Monte Carlo burnup in HTR system with various TRISO packing. Ann. Nucl. Energy 2016, 92, 419–430. [Google Scholar] [CrossRef]
- Wieselquist, W.A.; Lefebvre, R.A.; Jessee, M.A. SCALE Code System; ORNL/TM/2005/39; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 2020. [Google Scholar]
- Kloosterman, J.L.; Ougouag, A.M. Computation of Dancoff Factors for Fuel Elements Incorporating Randomly Packed Triso Particles; INEEL/EXT-05-02593; Idaho National Laboratory (INL): Idaho Falls, ID, USA, 2005. [Google Scholar]
- Mehta, K.S.; Goddard, B.; Wu, Z. A High-Fidelity Multiphysics Computational Model for Pebble Bed Gas Reactor based on Open-Source Software. In Proceedings of the 2024 ANS Student Conference, University Park, PA, USA, 4–6 April 2024. [Google Scholar]
- Mehta, K.; Goddard, B.; Wu, Z. Neutronics Analysis on High Temperature Gas Cooled Pebble Bed Reactors by Coupling Monte Carlo Method and Discrete Element Method. Energies 2024, 17, 5188. [Google Scholar] [CrossRef]
- Loza, P. TRISO-X Pebble Fuel Qualification Methodology; Xe-100 Topical Report; X-Energy: Rockville, MD, USA, 2021. [Google Scholar]
- Calabrese, R. Sustainability issues of plutonium recycling in light water reactors: Code evaluations up to 2050. Ann. Nucl. Energy 2013, 58, 268–271. [Google Scholar] [CrossRef]
- Dodd, B.; Britt, T.; Lloyd, C.; Shah, M.; Goddard, B. Novel Homogeneous Burnable Poisons in Pressurized Water Reactor Ceramic Fuel. Nucl. Eng. Technol. 2020, 52, 2874–2879. [Google Scholar] [CrossRef]
- Goddard, B.; Totemeier, A. Improved Disposition of Surplus Weapons-Grade Plutonium using a Metallic Pu-Zr Fuel Design. Nucl. Technol. 2023, 209, 696–706. [Google Scholar] [CrossRef]
- Goddard, B.; Solodov, A.; Fedchenko, V. IAEA “significant quantity” values: Time for a closer look? Nonproliferation Rev. 2016, 23, 677–689. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).