Two-Dimensional Fuel Assembly Study for a Supercritical Water-Cooled Small Modular Reactor
Abstract
1. Introduction
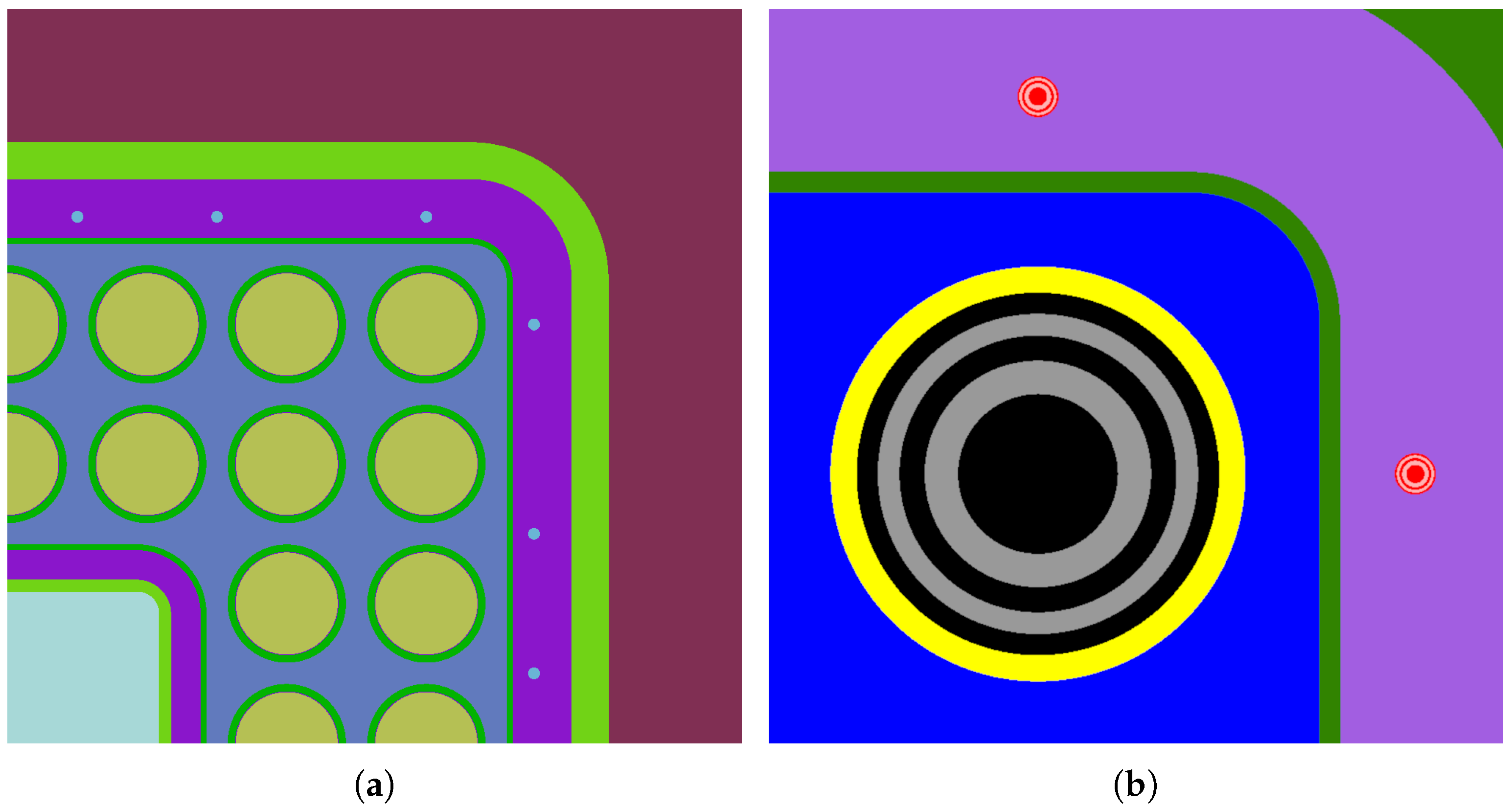
2. The SCW-SMR Fuel Assembly
3. Burnable Absorbers
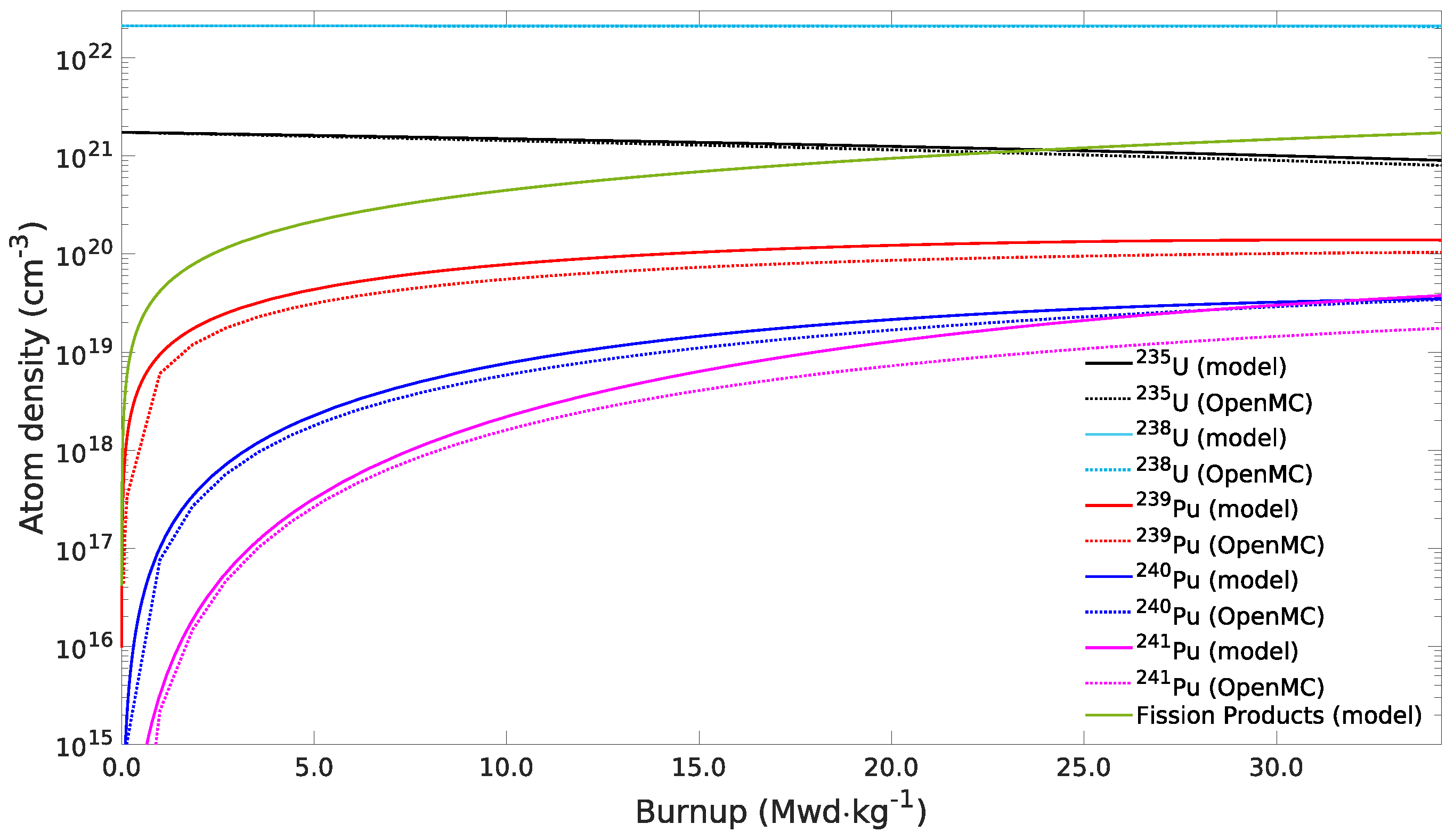
3.1. Simplified Analytical Model
3.2. Burnable Absorbers for the SCW-SMR Fuel Assembly—Analytical Study
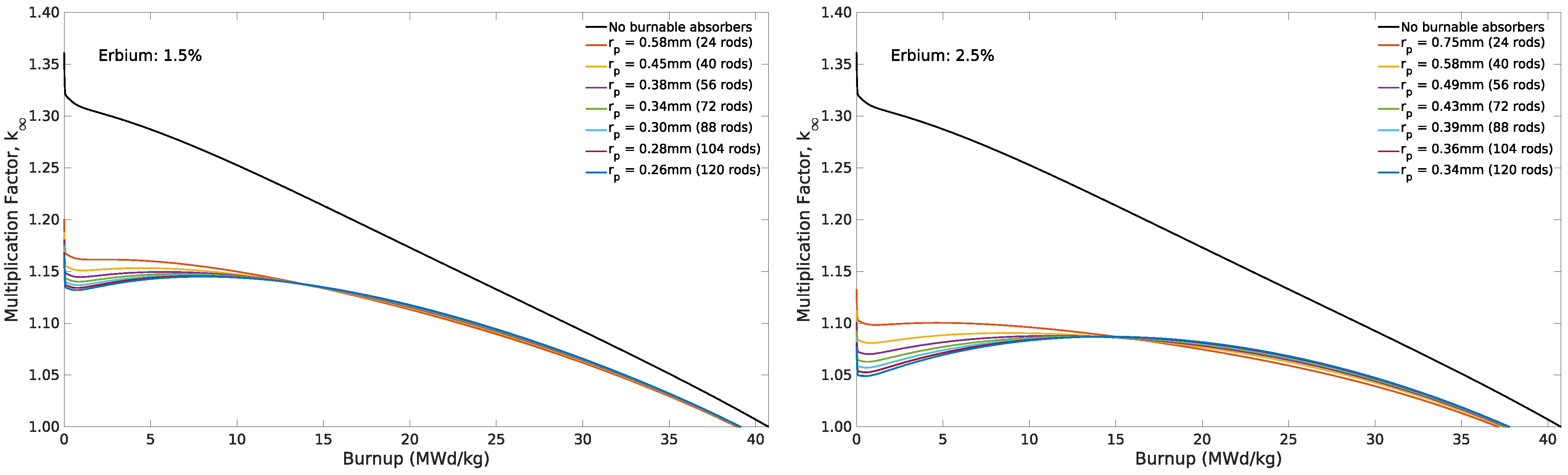
3.2.1. Erbium
3.2.2. Boron Carbide
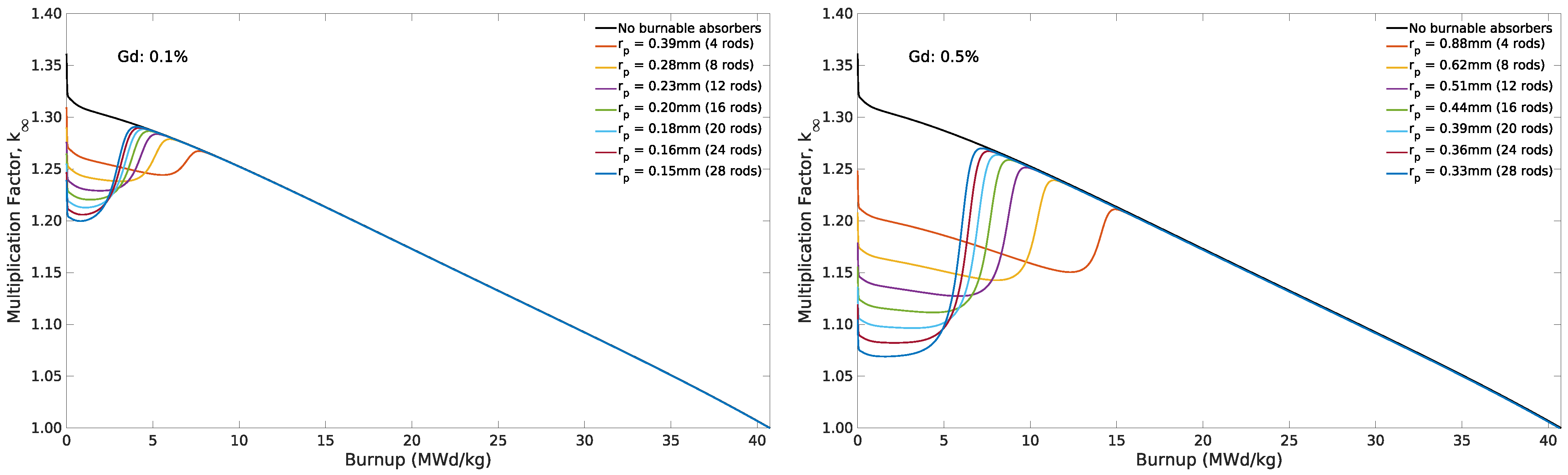
3.2.3. Gadolinium
3.3. Burnable Absorbers for the SCW-SMR Fuel Assembly—Monte Carlo Study
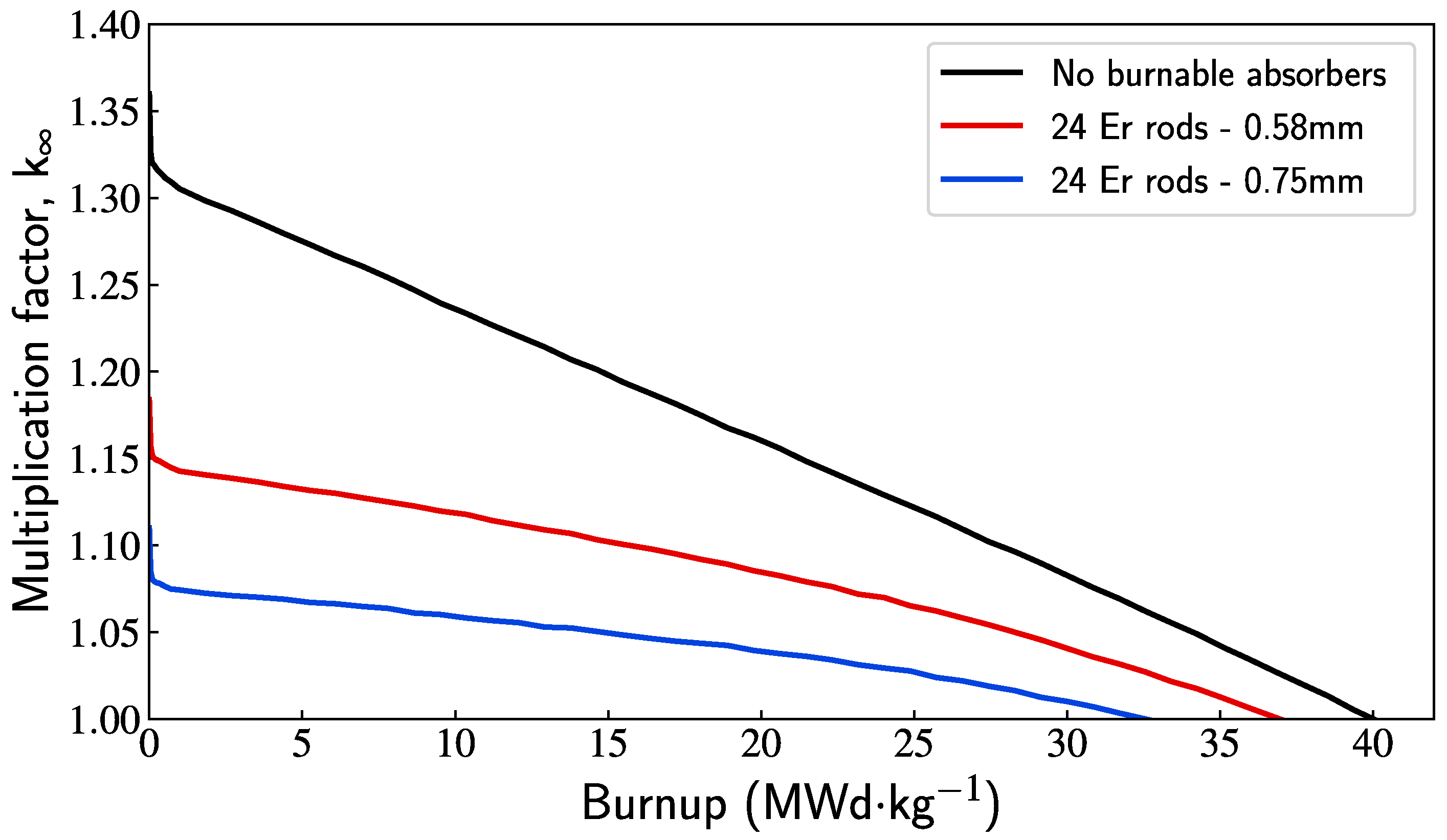
3.3.1. Erbium
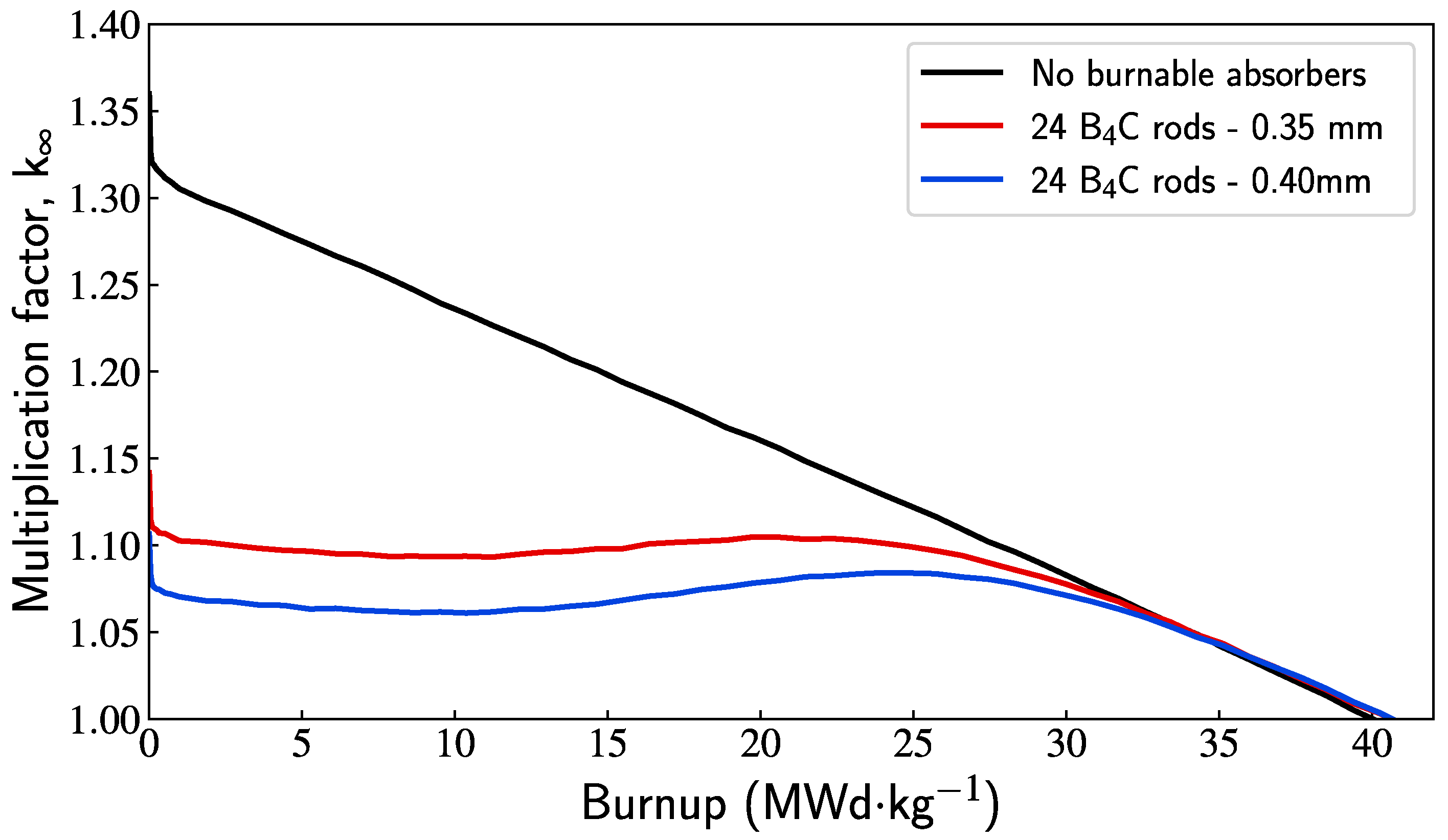
3.3.2. Boron Carbide
3.3.3. Gadolinium
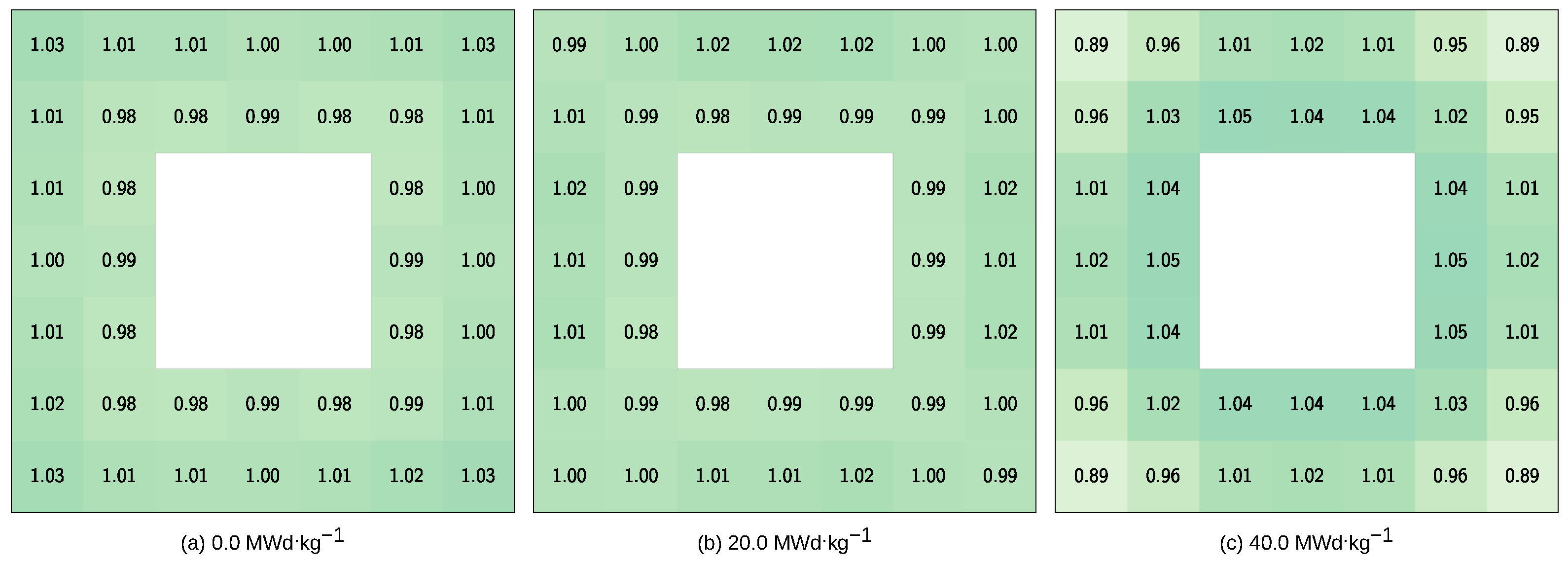
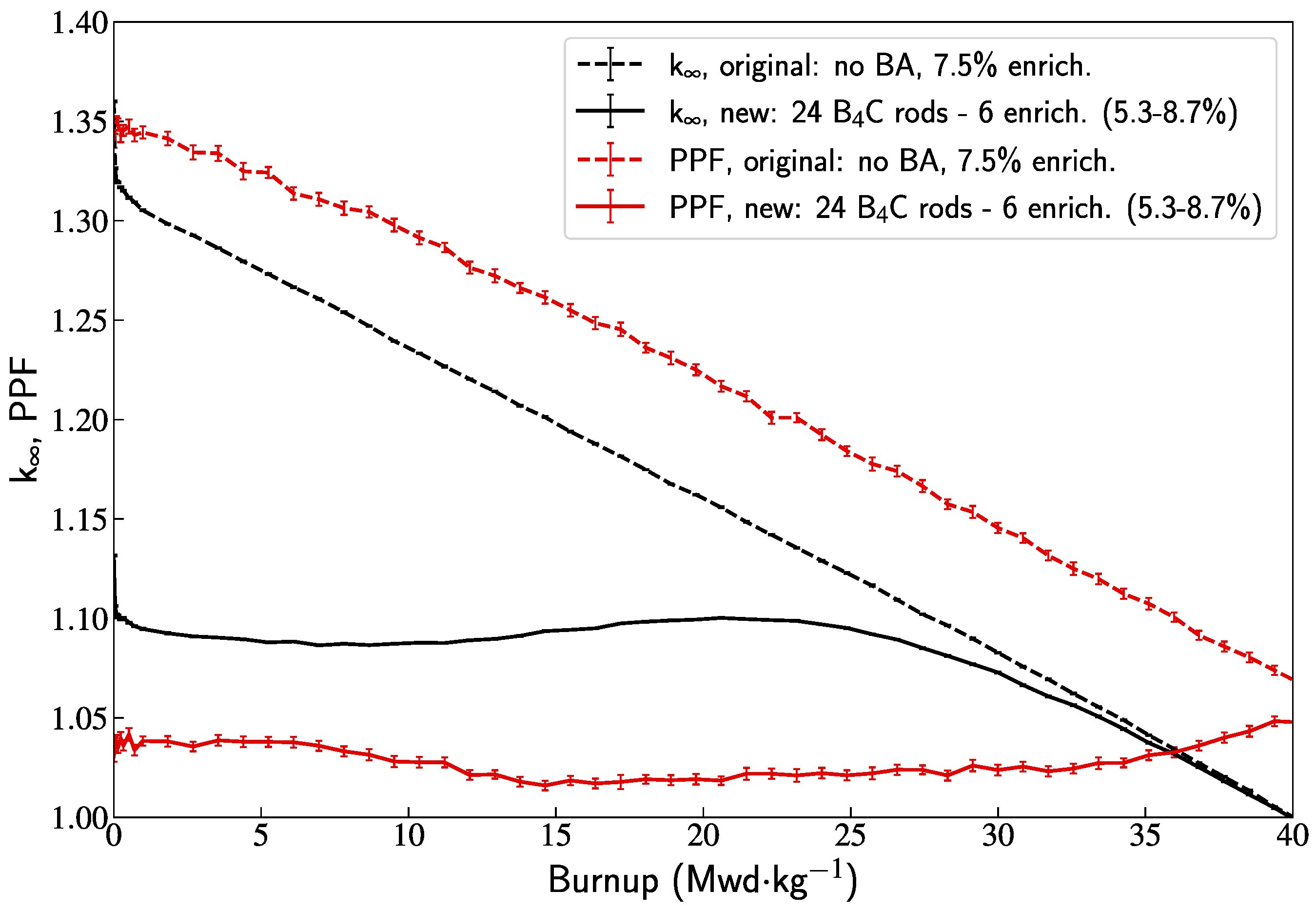
4. Assembly Pin-Power Peaking Factor
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Brook, B.W.; Alonso, A.; Meneley, D.A.; Misak, J.; Blees, T.; van Erp, J.B. Why nuclear energy is sustainable and has to be part of the energy mix. Sustain. Mater. Technol. 2014, 1–2, 8–16. [Google Scholar] [CrossRef]
- IAEA. Deployment Indicators for Small Modular Reactors; Number 1854 in Tecdoc Series; International Atomic Energy Agency: Vienna, Austria, 2018. [Google Scholar]
- IAEA. Small Modular Reactors: A New Nuclear Energy Paradigm; International Atomic Energy Agency: Vienna, Austria, 2022; Available online: https://smr.iaea.org (accessed on 4 July 2025).
- Lee, J.I. Review of Small Modular Reactors: Challenges in Safety and Economy to Success. Korean J. Chem. Eng. 2024, 41, 2761–2780. [Google Scholar] [CrossRef]
- Pioro, I.L.; Rodriguez, G.H. Chapter 2—Generation IV International Forum (GIF). In Handbook of Generation IV Nuclear Reactors, 2nd ed.; Pioro, I.L., Ed.; Woodhead Publishing Series in Energy; Woodhead Publishing: Cambridge, UK, 2023; pp. 111–132. [Google Scholar] [CrossRef]
- Starflinger, J.; Schulenberg, T. (Eds.) High Performance Light Water Reactor: Design and Analyses; KIT Scientific Publishing: Karlsruhe, Germany, 2012; p. 255. [Google Scholar] [CrossRef]
- Oka, Y.; Mori, H. Supercritical-Pressure Light Water Cooled Reactors; Springer: Tokyo, Japan, 2014. [Google Scholar] [CrossRef]
- Kryková, M.; Schulenberg, T.; Arnoult Růžičková, M.; Sáez-Maderuelo, A.; Otic, I.; Czifrus, S.; Cizelj, L.; Pavel, G.L. European Research Program on Supercritical Water-Cooled Reactor. J. Nucl. Eng. Radiat. Sci. 2020, 7, 021301. [Google Scholar] [CrossRef]
- Radkowsky, A. Theory and application of burnable poisons. In Proceedings of the 2nd United Nations International Conference on the Peaceful Uses of Atomic Energy, Geneva, Switzerland, 1–13 September 1958; Volume 13: Reactor Physics and Economics, pp. 426–445. [Google Scholar]
- Ohki, S. Fuel Burnup and Reactivity Control. In Nuclear Reactor Design; Oka, Y., Ed.; Springer: Tokyo, Japan, 2014; pp. 1–47. [Google Scholar] [CrossRef]
- Franceschini, F.; Petrović, B. Fuel with advanced burnable absorbers design for the IRIS reactor core: Combined Erbia and IFBA. Ann. Nucl. Energy 2009, 36, 1201–1207. [Google Scholar] [CrossRef]
- Choe, J.; Shin, H.C.; Lee, D. New burnable absorber for long-cycle low boron operation of PWRs. Ann. Nucl. Energy 2016, 88, 272–279. [Google Scholar] [CrossRef]
- Jo, Y.; Shin, H.C. Design optimization of cylindrical burnable absorber inserted into annular fuel pellets for soluble-boron-free SMR. Nucl. Eng. Technol. 2022, 54, 1464–1470. [Google Scholar] [CrossRef]
- Evans, J.A.; DeHart, M.D.; Weaver, K.D.; Keiser, D.D. Burnable absorbers in nuclear reactors—A review. Nucl. Eng. Des. 2022, 391, 111726. [Google Scholar] [CrossRef]
- Antók, C.; Czifrus, S.; Giusti, V. Neutronic calculations for preliminary core design of SCW-SMR. Ann. Nucl. Energy 2024, 209, 110805. [Google Scholar] [CrossRef]
- Schulenberg, T.; Otic, I. Suggestion for design of a small modular SCWR. In Proceedings of the 10th International Symposium on Supercritical WaterCooled Reactors (ISSCWR10), Prague, Czech Republic, 15–19 March 2021. Paper Number ISSCWR10-019. [Google Scholar]
- Leppänen, J.; Pusa, M.; Viitanen, T.; Valtavirta, V.; Kaltiaisenaho, T. The Serpent Monte Carlo code: Status, development and applications in 2013. Ann. Nucl. Energy 2015, 82, 142–150. [Google Scholar] [CrossRef]
- Allison, C.M.; Hohorst, J.K. Role of RELAP/SCDAPSIM in Nuclear Safety. Sci. Technol. Nucl. Install. 2010, 2010, 425658. [Google Scholar] [CrossRef]
- Meghreblian, R.; Holmes, D. Reactor Analysis; McGraw-Hill Series in Nuclear Engineering; McGraw-Hill: New York, NY, USA, 1960. [Google Scholar]
- Volkov, V.S.; Luk’yanov, A.S.; Chapkunov, V.V.; Shevyakov, V.P.; Yamnikov, V.S. Use of burnable poisons in nuclear reactors. Sov. J. At. Energy 1962, 11, 745–757. [Google Scholar] [CrossRef]
- Hurwitz, H.; Zweifel, P.F. Self-Shielding of Lumped-Poison Mixtures. Nucl. Sci. Eng. 1956, 1, 438–440. [Google Scholar] [CrossRef]
- Leonard, J.H.; Wackman, W. Lumped burnable poisons III—Applications. Trans. Am. Nucl. Soc. 1958, 1, 132–134. [Google Scholar]
- Yamashita, K. Optimization Method of Rod-Type Burnable Poisons for Nuclear Designs of HTGRs. J. Nucl. Sci. Technol. 1994, 31, 979–985. [Google Scholar] [CrossRef]
- Romano, P.K.; Horelik, N.E.; Herman, B.R.; Nelson, A.G.; Forget, B.; Smith, K. OpenMC: A state-of-the-art Monte Carlo code for research and development. Ann. Nucl. Energy 2015, 82, 90–97. [Google Scholar] [CrossRef]
- Zweifel, P. Reactor Physics; McGraw-Hill: New York, NY, USA, 1973. [Google Scholar]
- Henry, A. Nuclear-Reactor Analysis; MIT Press: Cambridge, MA, USA, 1975. [Google Scholar]
- Radkowsky, A.; Creagan, R.J. Poison control of thermal reactor. In Proceedings of the 3rd International Conference on the Peaceful Uses of Atomic Energy, Geneva, Switzerland, 31 August–9 September 1964; Volume 4: Reactor Control, pp. 277–284. [Google Scholar]
- McDonald, P.; Buongiorno, J.; Sterbentz, J.W.; Davis, C.; Witt, R. Feasibility Study of Supercritical Light Water Cooled Reactors for Electric Power Production. Nuclear Energy Research Initiative Project 2001-001, Westinghouse Electric Co. Grant Number: DE-FG07-02SF22533, Final Report. Available online: https://doi.org/10.2172/911007 (accessed on 4 July 2025).







| Steps | Length | Power | |
|---|---|---|---|
| h | Mwd·kg−1 | kW | |
| 3 | 24 | 0.046755 | 7.2 |
| 2 | 48 | 0.093510 | |
| 2 | 96 | 0.187020 | |
| 1 | 144 | 0.280532 | |
| 47 | 438 | 0.853285 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giusti, V. Two-Dimensional Fuel Assembly Study for a Supercritical Water-Cooled Small Modular Reactor. J. Nucl. Eng. 2025, 6, 26. https://doi.org/10.3390/jne6030026
Giusti V. Two-Dimensional Fuel Assembly Study for a Supercritical Water-Cooled Small Modular Reactor. Journal of Nuclear Engineering. 2025; 6(3):26. https://doi.org/10.3390/jne6030026
Chicago/Turabian StyleGiusti, Valerio. 2025. "Two-Dimensional Fuel Assembly Study for a Supercritical Water-Cooled Small Modular Reactor" Journal of Nuclear Engineering 6, no. 3: 26. https://doi.org/10.3390/jne6030026
APA StyleGiusti, V. (2025). Two-Dimensional Fuel Assembly Study for a Supercritical Water-Cooled Small Modular Reactor. Journal of Nuclear Engineering, 6(3), 26. https://doi.org/10.3390/jne6030026






