Cost-Optimal Design of a Stand-Alone PV-Driven Hydrogen Production and Refueling Station Using Genetic Algorithms
Abstract
1. Introduction
2. Materials and Methods
2.1. System Configuration
2.2. Optimization Framework
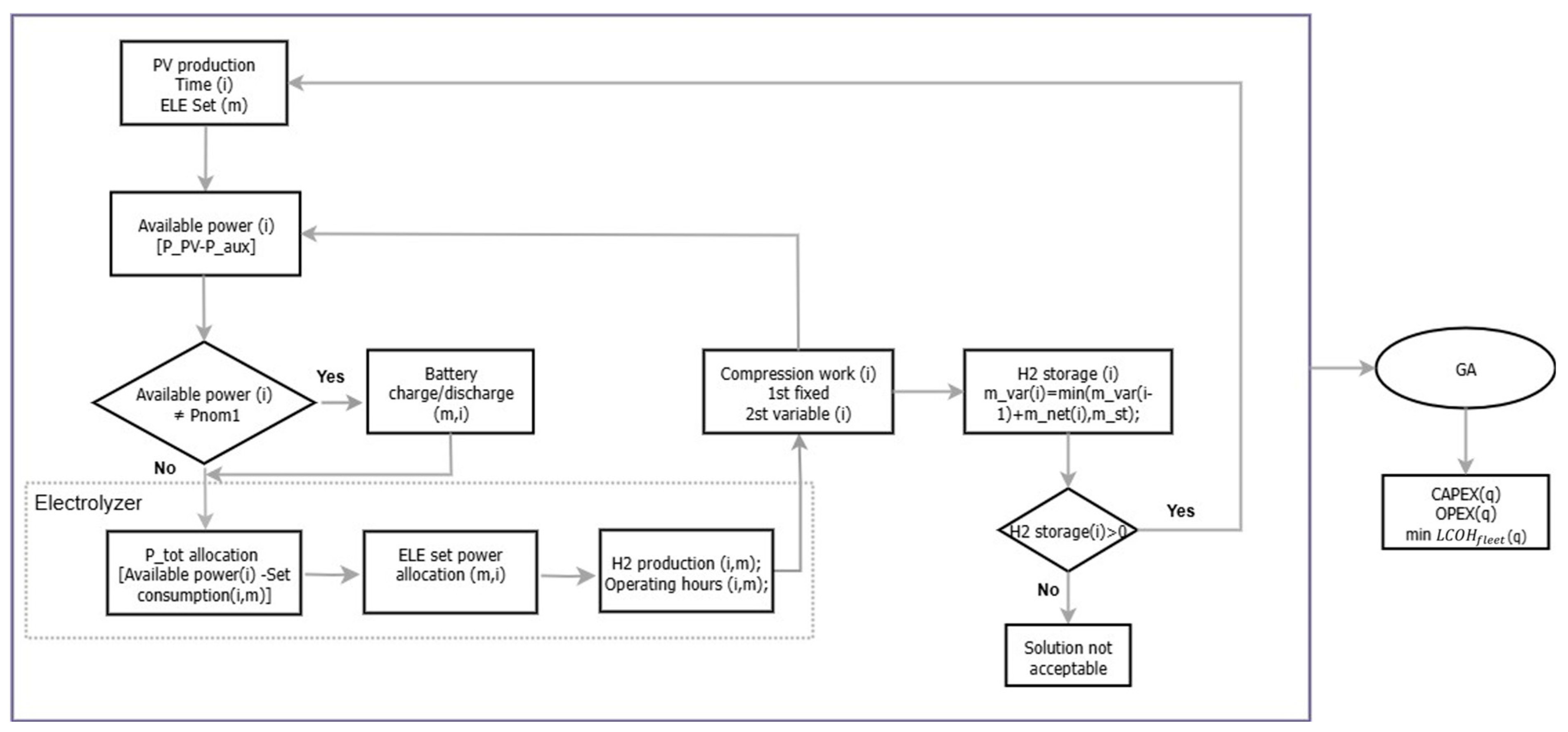
2.3. Description of the Solution Method
Simulation Logic
- Step 1: Based on hourly meteorological data, PV generation is quantified. For each timestep, the model verifies whether the available power covers the auxiliary loads of the electrolyzer and compressor. Any surplus is allocated to hydrogen production, while deviations from nominal electrolyzer power are balanced by charging or discharging the battery.
- Step 2: The produced hydrogen is compressed and sent to storage. A mass balance check ensures that the stored hydrogen remains within operational limits. Configurations that result in insufficient storage are discarded as infeasible.
- Step 3: At each cycle, the GA evaluates candidate solutions in terms of CAPEX, OPEX, and . Based on these metrics, the algorithm performs selection, crossover, and mutation to evolve toward the configuration that minimizes the objective function, ensuring compliance with all technical and economic requirements.
2.4. Governing Equations of the System Components
2.5. Model Limitations
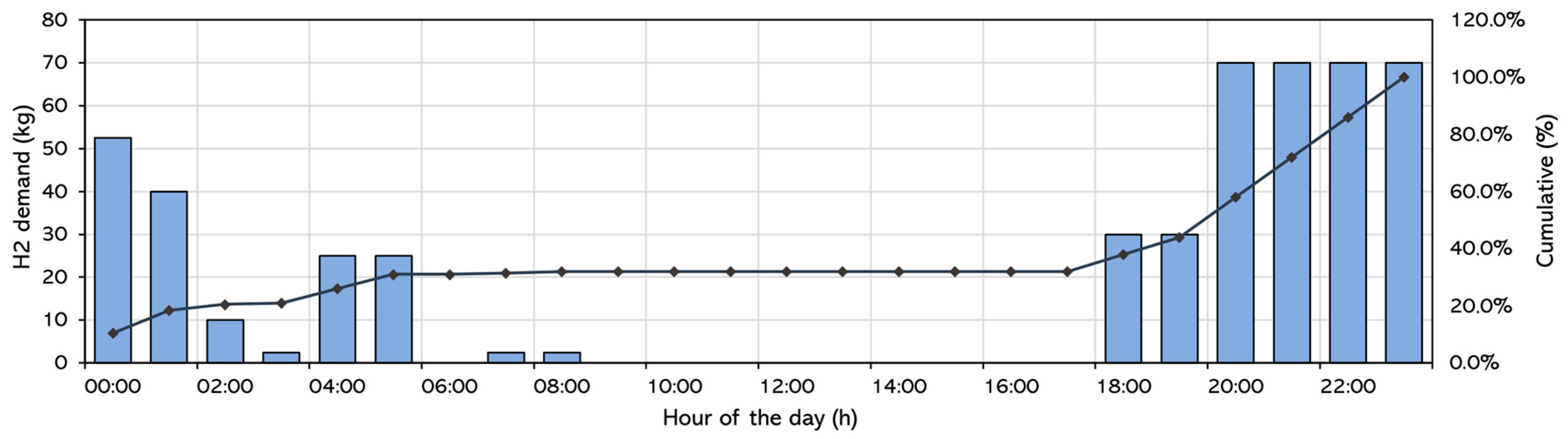
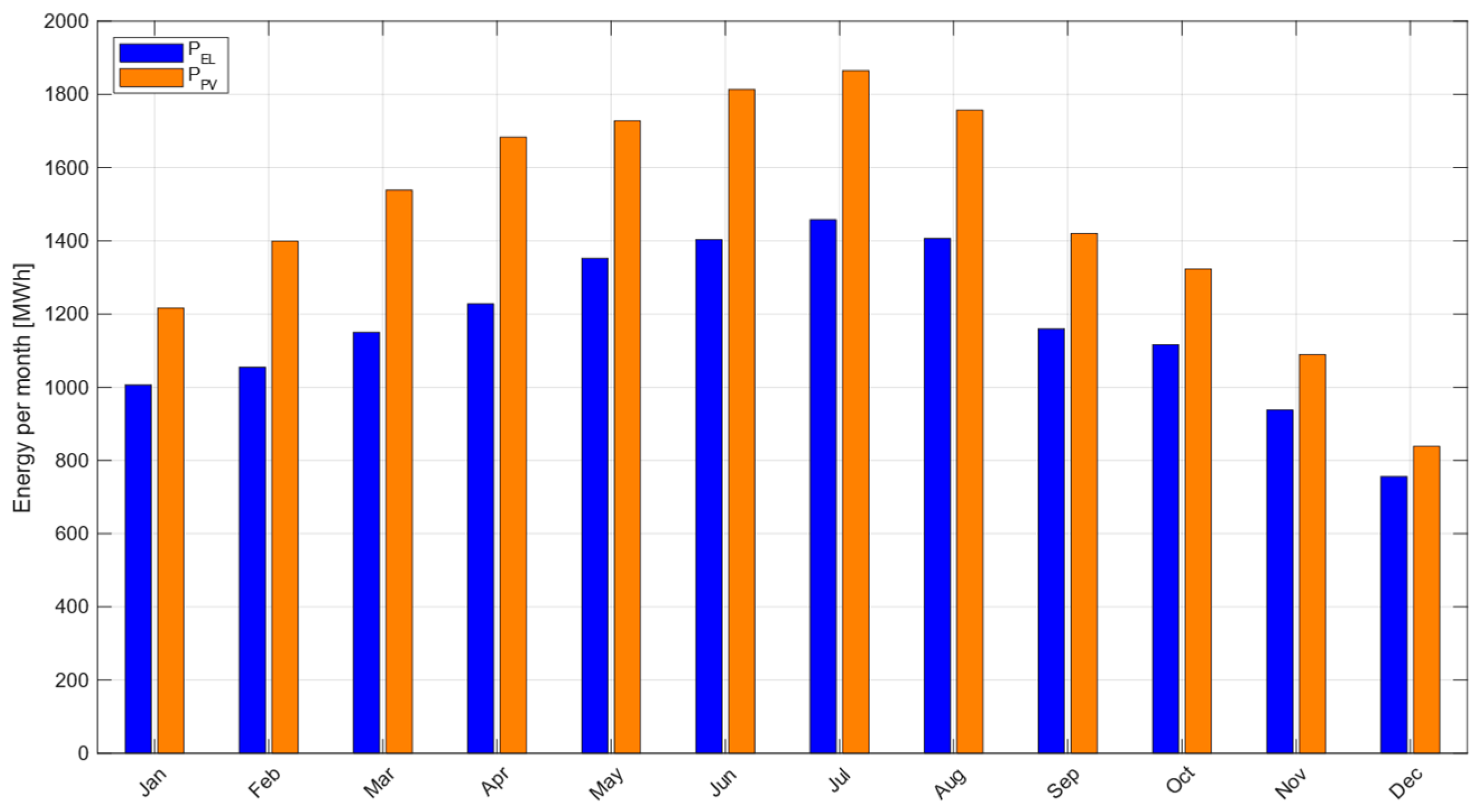
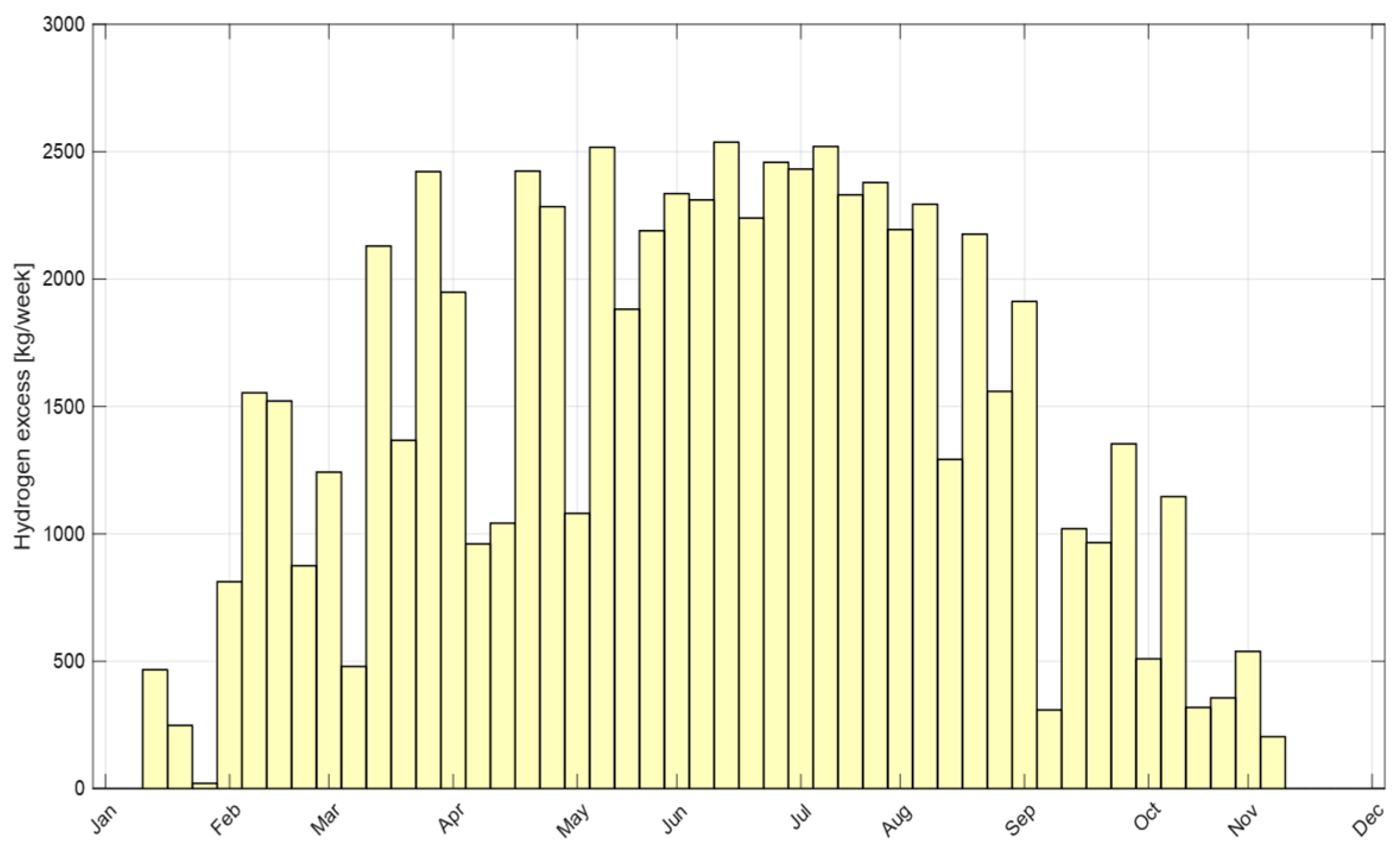
3. Results and Discussion
3.1. GA Optimization Results
3.2. Economic Viability of the Investment
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| η | Efficiency, % |
| c | Capacity, kWh |
| E | Energy, kWh |
| H | Enthalpy, kJ/kg |
| m | Mass, kg |
| N | Number |
| p | Price, €/kg |
| P | Power, kW |
| Q | Heat transfer, kW |
| t | Time, h |
| W | Work, kW |
| Acronyms | |
| BESS | Battery energy storage system |
| BEV | Battery electric vehicle |
| CAPEX | Capital cost of expenditure |
| CF | Capacity factor |
| EU | European Union |
| FCEV | Fuel cell electric vehicle |
| GA | Genetic algorithm |
| GHG | Greenhouse gas emissions |
| H2 | Hydrogen |
| HDV | Heavy-duty vehicle |
| HOMER | Hybrid optimization of multiple energy resources |
| HRS | Hydrogen refueling station |
| ICE | Internal combustion engine |
| IRR | Internal rate return |
| LCOH | Levelized cost of hydrogen |
| LCOH-T | Levelized cost of hydrogen for transport |
| LHV | Low heating value |
| NREL | National Renewable Energy Laboratory |
| O&M | Operation and maintenance |
| OPEX | Operational cost of expenditure |
| PEM | Proton exchange membrane |
| PV | Photovoltaic |
| REPLEX | Replacement cost |
| SOC | State of charge |
| TCO | Total cost of ownership |
| TTW | Tank-to-wheel |
| VAT | Value Added Tax |
| Subscripts | |
| 1st | First stage |
| 2st | Second stage |
| a | Annualized |
| b, batt | Battery |
| c | Compression |
| ch | Charge |
| d | Diesel |
| dem | Demand |
| dish | Discharge |
| el | Electrolyzer |
| fin | Final |
| fix | Fixed |
| in | Initial |
| is | Isentropic |
| min | Minimum |
| nom | Nominal |
| sys | System |
| st | Storage |
| var | Variable |
References
- Erbach, G. Regulation (EU) 1119. In European Climate Law; European Commission: Brussel, Belgium, 2021. [Google Scholar]
- European Environment Agency. Greenhouse Gas Emissions from Transport in Europe. EEA. Available online: https://www.eea.europa.eu/en/analysis/indicators/greenhouse-gas-emissions-from-transport (accessed on 1 September 2025).
- European Environment Agency. Reducing Greenhouse Gas Emissions from Heavy-Duty Vehicles in Europe. EEA. Available online: https://www.eea.europa.eu/en/analysis/publications/reducing-greenhouse-gas-emissions-from-heavy-duty-vehicles-in-europe?activeTab=4dc6e920-0511-4a13-9e54-cdf81d43511f (accessed on 1 September 2025).
- European Environment Agency. Sustainability of Europe’s Mobility Systems; European Environment Agency: Copenhagen, Denmark, 2024. [CrossRef]
- Bhuiyan, M.M.H.; Siddique, Z. Hydrogen as an alternative fuel: A comprehensive review of challenges and opportunities in production, storage, and transportation. Int. J. Hydrogen Energy 2025, 102, 1026–1044. [Google Scholar] [CrossRef]
- Mulholland, E.; Miller, J.; Braun, C.; Sen, A.; Ragon, P.-L.; Rodríguez, F. The CO2 Standards Required for Trucks and Buses for Europe to Meet Its Climate Targets. International Council on Clean Transportation. 2022. Available online: https://theicct.org/publication/hdv-co2standards-recs-mar22/ (accessed on 1 September 2025).
- Grzelakowski, A.S. Market and Regulatory Challenges of the EU Road Freight Transport Transformation towards Zero Emissions. Eur. Res. Stud. J. 2025, XXVIII, 680–695. [Google Scholar] [CrossRef]
- Eurostat. EU People on the Move in 2022. Available online: https://ec.europa.eu/eurostat/web/products-eurostat-news/w/ddn-20240916-1 (accessed on 1 September 2025).
- IEA. The Future of Hydrogen; IEA: Paris, France, 2019.
- Kleen, G.; Gibbons, W. Heavy-Duty Fuel Cell System Cost—2023; U.S. Department of Energy: Washington, DC, USA, 2024.
- Bracci, J.; Koleva, M.; Chung, M. Levelized Cost of Dispensed Hydrogen for Heavy-Duty Vehicles; No. NREL/TP-5400-88818; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2024.
- Catsaros, O. Lithium-Ion Battery Pack Prices See Largest Drop Since 2017, Falling to $115 per Kilowatt-Hour; BloombergNEF: London, UK, 2024. [Google Scholar]
- Ahluwalia, R.K.; Wang, X.; Papadias, D.D.; Star, A.G. Performance and Total Cost of Ownership of a Fuel Cell Hybrid Mining Truck. Energies 2023, 16, 286. [Google Scholar] [CrossRef]
- De Wolf, D.; Smeers, Y. Comparison of Battery Electric Vehicles and Fuel Cell Vehicles. World Electr. Veh. J. 2023, 14, 262. [Google Scholar] [CrossRef]
- Hussein, B.; Rodríguez, F. A Total Cost of Ownership Comparison of Truck Decarbonization Pathways in Europe; International Council on Clean Transportation: Washington, DC, USA, 2023; pp. 1–35. [Google Scholar]
- Danielis, R.; Scorrano, M.; Masutti, M.; Awan, A.M.; Niazi, A.M.K. The Economic Competitiveness of Hydrogen Fuel Cell-Powered Trucks: A Review of Total Cost of Ownership Estimates. Energies 2024, 17, 2509. [Google Scholar] [CrossRef]
- Nnabuife, S.G.; Hamzat, A.K.; Whidborne, J.; Kuang, B.; Jenkins, K.W. Integration of renewable energy sources in tandem with electrolysis: A technology review for green hydrogen production. Int. J. Hydrogen Energy 2025, 107, 218–240. [Google Scholar] [CrossRef]
- Jolly, S.S.; Twinkle, A.R.; Sasi, B.S.A.; Reshma, R. Emerging paradigms in renewable hydrogen production: Technology, challenges, and global impact. Next Energy 2025, 8, 343. [Google Scholar] [CrossRef]
- Titheridge, L.J.; Marshall, A.T. Techno-economic modelling of AEM electrolysis systems to identify ideal current density and aspects requiring further research. Int. J. Hydrogen Energy 2024, 49, 518–532. [Google Scholar] [CrossRef]
- European Hydrogen Observatory. Clean Hydrogen Observatory. In Levelised Cost of Hydrogen (LCOH) Calculator Manual; European Hydrogen Observatory: Brussels, Belgium, 2024. [Google Scholar]
- Prokopou, G.I.; Faust, J.M.M.; Mitsos, A.; Bongartz, D. Cost-optimal design and operation of hydrogen refueling stations with mechanical and electrochemical hydrogen compressors. Comput. Chem. Eng. 2025, 192, 108862. [Google Scholar] [CrossRef]
- Chen, G.; Su, S.; Xu, Q.; Lv, H.; Zhao, Y.; Xia, L.; Zhang, G.; Hu, K. Optimization of hydrogen refueling strategy: Based on energy consumption and refueling demand. Int. J. Hydrogen Energy 2024, 71, 625–636. [Google Scholar] [CrossRef]
- Genovese, M.; Fragiacomo, P. Hydrogen station evolution towards a poly-generation energy system. Int. J. Hydrogen Energy 2022, 47, 12264–12280. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, W.; He, Y.; Zhang, H.; Chen, W.; Yang, C.; Dong, H. Capacity Optimization of Renewable-Based Hydrogen Production–Refueling Station for Fuel Cell Electric Vehicles: A Real-Project-Based Case Study. Sustainability 2025, 17, 7311. [Google Scholar] [CrossRef]
- Kim, G.-W.; Park, S.-W.; Son, S.-Y. Techno-Economic Optimal Operation of an On-Site Hydrogen Refueling Station. Appl. Sci. 2025, 15, 10999. [Google Scholar] [CrossRef]
- Mansir, I.B. Design and optimization of hydrogen refueling station powered by hybrid energy system. J. Renew. Sustain. Energy 2025, 17, 046302. [Google Scholar] [CrossRef]
- Okonkwo, P.C.; Nwokolo, S.C.; Alarifi, S.S.; Ekwok, S.E.; Orji, R.; Udo, S.O.; Eldosouky, A.M.; Barhoumi, E.M.; Das, B.K.; Gomez-Ortiz, D.; et al. Bio-inspired computational intelligence metaheuristic-based optimization and sensitivity analysis approach to determine techno-economic feasibility of hydrogen refueling stations for fuel cell vehicles. Sci. Rep. 2025, 15, 12451. [Google Scholar] [CrossRef]
- Oueslati, F. HOMER optimization of standalone PV/Wind/Battery powered hydrogen refueling stations located at twenty selected French cities. Int. J. Renew. Energy Dev. 2023, 12, 1070–1090. [Google Scholar] [CrossRef]
- Al-Sharafi, A.; Al-Buraiki, A.S.; Al-Sulaiman, F.; Antar, M.A. Hydrogen refueling stations powered by hybrid PV/wind renewable energy systems: Techno-socio-economic assessment. Energy Convers. Manag. X 2024, 22, 100584. [Google Scholar] [CrossRef]
- Arunachalam, M.; Han, D.S. Efficient solar-powered PEM electrolysis for sustainable hydrogen production: An integrated approach. Emergent. Mater. 2024, 7, 1401–1415. [Google Scholar] [CrossRef]
- Hong, F.T.; Lin, H.; Vazquez-Sanchez, H.; Xue, X.; Li, Y.; Zhang, L.; Sarathy, S.M. Minimizing renewable hydrogen costs at producer’s terminal gate with alkaline electrolyser, proton exchange membrane, and their co-installment: A regional case study in China. Int. J. Hydrogen Energy 2024, 86, 1051–1062. [Google Scholar] [CrossRef]
- Liu, L.; Ma, H.; Khan, M.; Hsiao, B.S. Recent Advances and Challenges in Anion Exchange Membranes Development/Application for Water Electrolysis: A Review. Membranes 2024, 14, 85. [Google Scholar] [CrossRef]
- Apostolou, D.; Xydis, G. A literature review on hydrogen refuelling stations and infrastructure. Current status and future prospects. Renew. Sustain. Energy Rev. 2019, 113, 109292. [Google Scholar] [CrossRef]
- Caponi, R.; Bocci, E.; Del Zotto, L. Techno-Economic Model for Scaling Up of Hydrogen Refueling Stations. Energies 2022, 15, 7518. [Google Scholar] [CrossRef]
- IEA. Global Hydrogen Review 2024; IEA: Paris, France, 2024.
- H2 mobility. Overview Hydrogen Refuelling for Heavy Duty Vehicles; H2 Mobility: Berlin, Germany, 2021. [Google Scholar]
- Caponi, R.; Ferrario, A.M.; Del Zotto, L.; Bocci, E. Hydrogen refueling stations and fuel cell buses four year operational analysis under real-world conditions. Int. J. Hydrogen Energy 2022, 48, 20957–20970. [Google Scholar] [CrossRef]
- Gunawan, T.A.; Williamson, I.; Raine, D.; Monaghan, R.F.D. Decarbonising city bus networks in Ireland with renewable hydrogen. Int. J. Hydrogen Energy 2021, 46, 28870–28886. [Google Scholar] [CrossRef]
- Sayer, M.; Ajanovic, A.; Haas, R. On the economics of a hydrogen bus fleet powered by a wind park—A case study for Austria. Int. J. Hydrogen Energy 2022, 47, 33153–33166. [Google Scholar] [CrossRef]
- FCH-JU. New Bus ReFuelling for European Hydrogen Bus Depots. Guidance Document on Large Scale Hydrogen Bus Refuelling. 2017. Available online: https://www.fuelcellbuses.eu/ (accessed on 3 July 2025).
- MATLAB, Version 9.13 (R2022b); MATLAB: Natick, MA, USA, 2022.
- Vizza, D.; Caponi, R.; Bocci, E.; Del Zotto, L.; Bassano, C. Cost effective hydrogen production of coupled photovoltaic and electrolyzer systems considering plant lifetime and geographical location. Energy Convers. Manag. X 2025, 27, 101136. [Google Scholar] [CrossRef]
- Photovoltaic Geographical Information System (PVGIS). Version 5.2. 2017. Available online: https://re.jrc.ec.europa.eu/pvg_tools/en/#MR (accessed on 3 July 2025).
- Alshamri, H.; Cockerill, T.; Tomlin, A.S.; Al-Damook, M.; Al Qubeissi, M. On–off-Grid Optimal Hybrid Renewable Energy Systems for House Units in Iraq. Clean Technol. 2024, 6, 602–624. [Google Scholar] [CrossRef]
- Hettesheimer, T.; Neef, C.; Rosellón Inclán, I.; Link, S.; Schmaltz, T.; Schuckert, F.; Stephan, A.; Stephan, M.; Thielmann, A.; Weymann, L.; et al. Lithium-Ion Battery Roadmap—Industrialization Perspectives Toward 2030; Fraunhofer Institute for Systems and Innovation Research ISI: Karlsruhe, Germany, 2023. [Google Scholar] [CrossRef]
- Marocco, P.; Gandiglio, M.; Cianella, R.; Capra, M.; Santarelli, M. Design of hydrogen production systems powered by solar and wind energy: An insight into the optimal size ratios. Energy Convers. Manag. 2024, 314, 118646. [Google Scholar] [CrossRef]
- Klell, M. Storage of Hydrogen in the Pure Form. In Handbook of Hydrogen Storage: New Materials for Future Energy Storage; Hirscher, M., Ed.; Wiley-VCH Verlag GmbH & Co.: Weinheim, Germany, 2010; pp. 1–37. [Google Scholar] [CrossRef]
- Zheng, Y.; Huang, C.; Tan, J.; You, S.; Zong, Y.; Træholt, C. Off-grid wind/hydrogen systems with multi-electrolyzers: Optimized operational strategies. Energy Convers. Manag. 2023, 295, 117622. [Google Scholar] [CrossRef]
- U.S. Department of Energy. Pathways to Commercial Liftoff: Clean Hydrogen; U.S. Department of Energy: Washington, DC, USA, 2024.
- Seeger, K.; Genovese, M.; Schlüter, A.; Kockel, C.; Corigliano, O.; Díaz Canales, E.B.; Praktiknjo, A.; Fragiacomo, P. Techno-economic analysis of hydrogen and green fuels supply scenarios assessing three import routes: Canada, Chile, and Algeria to Germany. Int. J. Hydrogen Energy 2025, 116, 558–576. [Google Scholar] [CrossRef]
- Caponi, R.; Bocci, E.; Del Zotto, L. On-site hydrogen refuelling station techno-economic model for a fleet of fuel cell buses. Int. J. Hydrogen Energy 2024, 71, 691–700. [Google Scholar] [CrossRef]
- Pivetta, D.; Dall’armi, C.; Taccani, R. Multi-Objective Optimization of a Hydrogen Hub for the Decarbonization of a Port Industrial Area. J. Mar. Sci. Eng. 2022, 10, 231. [Google Scholar] [CrossRef]
- Franco, A.; Giovannini, C. Hydrogen Gas Compression for Efficient Storage: Balancing Energy and Increasing Density. Hydrogen 2024, 5, 293–311. [Google Scholar] [CrossRef]
- Caponi, R.; Vizza, D.; Bassano, C.; Del Zotto, L.; Bocci, E. Dynamic Comparative Assessment of Long-Term Simulation Strategies for an Off-Grid PV–AEM Electrolyzer System. Energies 2025, 18, 4209. [Google Scholar] [CrossRef]
- Röck, M.; Martin, R.; Hausberger, S. JEC Tank-to-Wheels Report v5: Heavy Duty Vehicles; European Commission: Brussel, Belgium, 2020. [CrossRef]
- Basma, H.; Rodríguez, F. Fuel cell electric tractor-trailers: Technology overview and fuel economy. In International Council on Clean Transportation Working Paper; International Council on Clean Transportation: Washington, DC, USA, 2022; Volume Working Paper 23. [Google Scholar]
- Hjelkrem, O.A.; Arnesen, P.; Bø, T.A.; Sondell, R.S. Estimation of tank-to-wheel efficiency functions based on type approval data. Appl. Energy 2020, 276, 115463. [Google Scholar] [CrossRef]
- European Commission. Weekly Oil Bulletin. Available online: https://energy.ec.europa.eu/data-and-analysis/weekly-oil-bulletin_en?utm_source=chatgpt.com (accessed on 3 September 2025).
- Penev, M.; Gilbert, A.; Rustagi, N.; Kee, J.; Koleva, M.; Chung, M. Capital Structure for Techno-Economic Analysis of Hydrogen Projects; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2024. Available online: https://www.nrel.gov/docs/fy24osti/90103.pdf (accessed on 3 September 2025).


| RE Supply | CAPEX (€/kW) [42] | OPEX (€/kW/Year) [42] | Lifetime (Year) [31] | Parameter Settings [42,43] |
|---|---|---|---|---|
| Solar PV | 700 | 2% total CAPEX | 20 | single-axis tracking, system loss 10%, PV degradation 0.3% after first year |
| Parameters | Unit | Value | Ref. |
|---|---|---|---|
| C-rate | - | 2 | [44] |
| CAPEX | €/kWh | 140 | [45] |
| OPEX | €/kWh/year | 2% CAPEX | [46] |
| REPLEX | €/kWh | 50% CAPEX | [46] |
| Lifetime | years | 10 | [46] |
| Parameters | Unit | Value | Ref. |
|---|---|---|---|
| Specific energy consumption | kWh/Nm3 (5–30%) kWh/Nm3 (30–60%) kWh/Nm3 (60–100%) | 4.9 5.5 4.8 | [48] |
| Dynamic working load range | % of rated power | 5–100% | [46] |
| CAPEX | €/kW | 1200 | [49] |
| OPEX | €/kW/year | 3% CAPEX | [46] |
| REPLEX | €/kW | 45% CAPEX | [42] |
| Lifetime of the stack | hours | 80,000 | [50] |
| Parameters | Unit | Value | Ref. |
|---|---|---|---|
| Storage pressure | bar | 500 | [51] |
| CAPEX | €/kg | 900 | [51] |
| OPEX | €/year | 0.5% CAPEX | [51] |
| Lifetime | years | 20 | [52] |
| Parameters | Unit | Value | Ref. |
|---|---|---|---|
| Suction/final pression | bar | 30/500 | [51] |
| Intercooling temperature | K | 288 | [51] |
| Compressor efficiency | % | 80 | [31] |
| Energy consumption average | kWh/kgH2 | 1.35 | [53] |
| CAPEX | €/kg | 43,872·(Wc)0.5861 | [51] |
| OPEX | €/year | 3% CAPEX | [31] |
| Lifetime | years | 20 | [21] |
| Parameters | Unit | Results |
|---|---|---|
| PV nominal power | MWp | 11 |
| Electrolyzer nominal power | MW | 4 |
| Battery capacity | MWh | 7 |
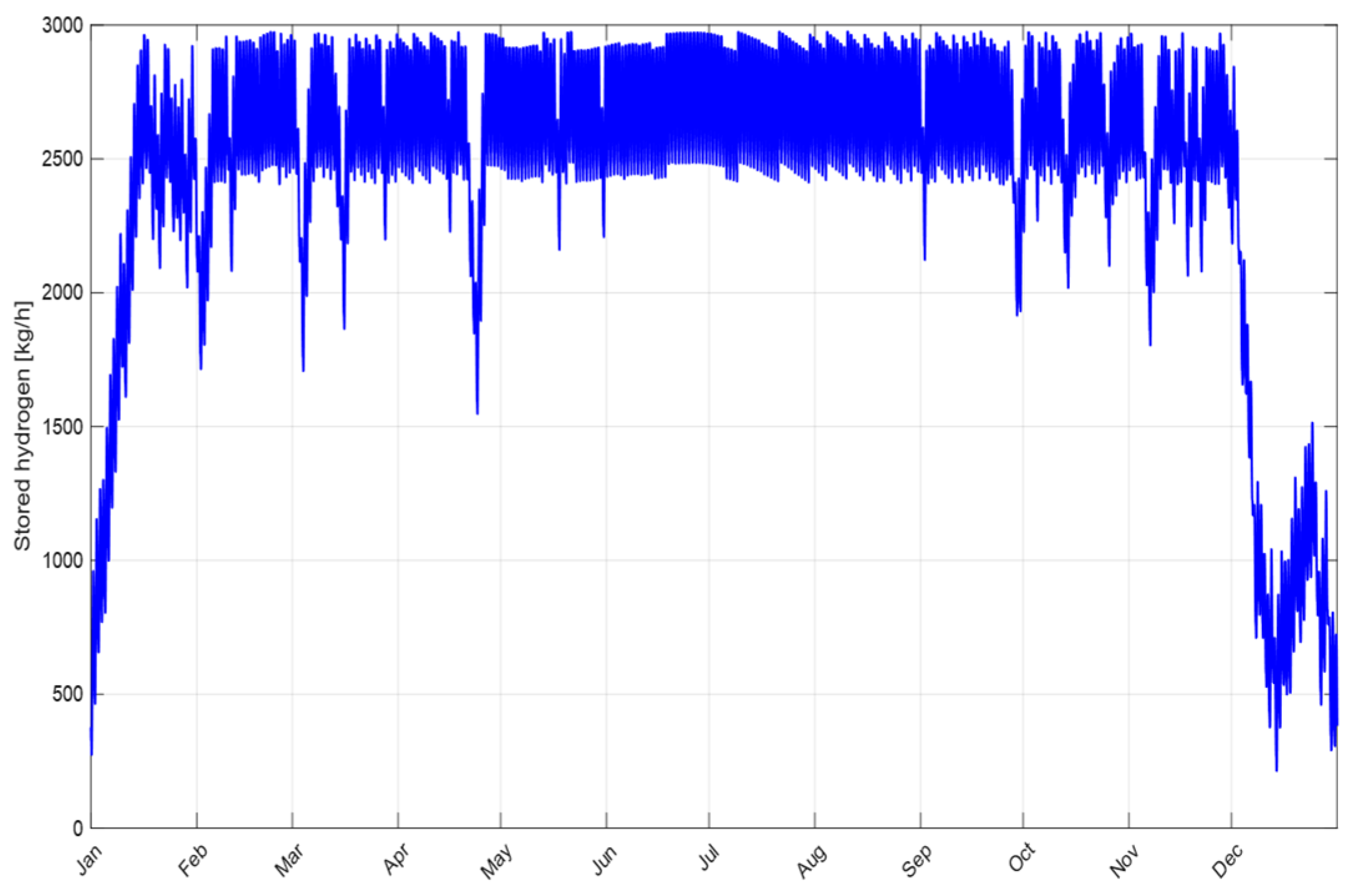
| Storage capacity | kg | 2900 |
| Total H2 production | kg/year | 251,607 |
| Total H2 excess | kg/year | 69,107 |
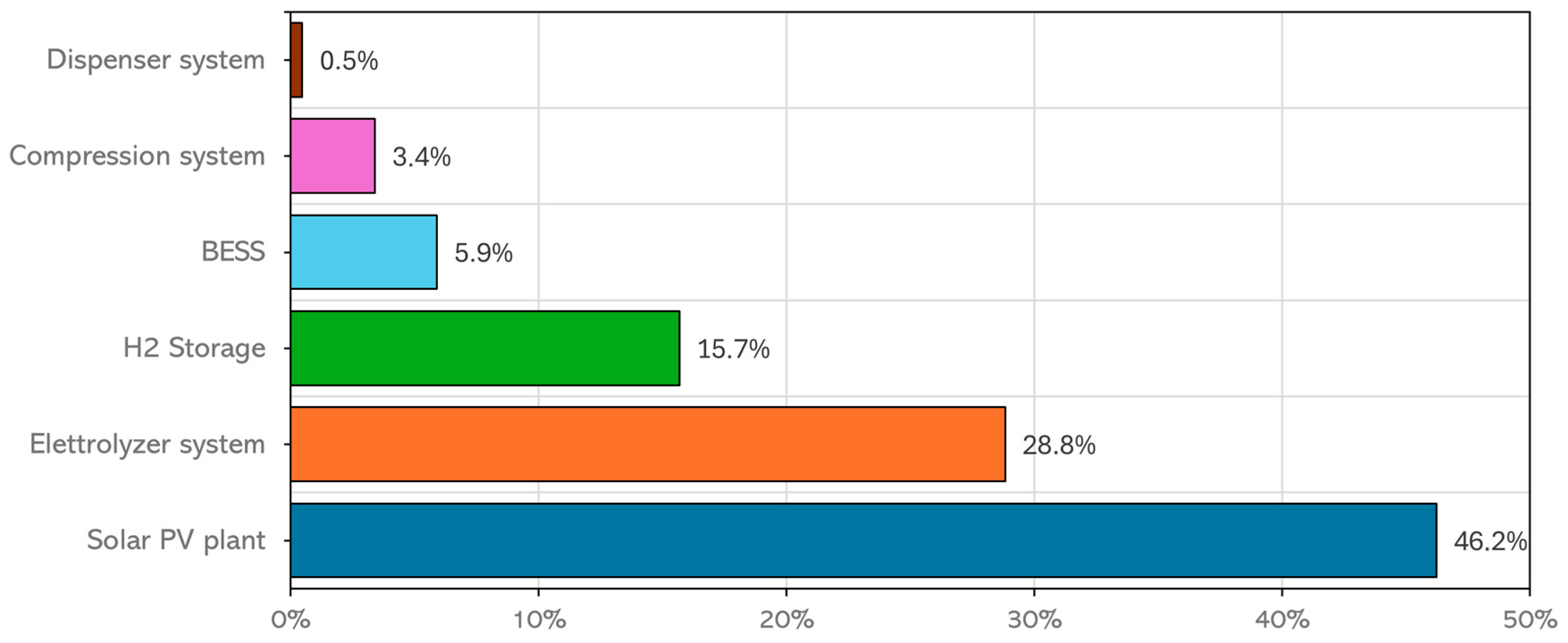
| CAPEX | M€ | 16.72 |
| CAPEXa | €/year | 1,458,519.58 |
| OPEX | €/year | 330,258.38 |
| REPLEX | M€ | 4.51 |
| REPLEXa | €/year | 219,783.76 |
| €/kg | 11.00 | |
| LCOH | €/kg | 7.98 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vizza, D.; Caponi, R.; Di Matteo, U.; Bocci, E. Cost-Optimal Design of a Stand-Alone PV-Driven Hydrogen Production and Refueling Station Using Genetic Algorithms. Hydrogen 2025, 6, 98. https://doi.org/10.3390/hydrogen6040098
Vizza D, Caponi R, Di Matteo U, Bocci E. Cost-Optimal Design of a Stand-Alone PV-Driven Hydrogen Production and Refueling Station Using Genetic Algorithms. Hydrogen. 2025; 6(4):98. https://doi.org/10.3390/hydrogen6040098
Chicago/Turabian StyleVizza, Domenico, Roberta Caponi, Umberto Di Matteo, and Enrico Bocci. 2025. "Cost-Optimal Design of a Stand-Alone PV-Driven Hydrogen Production and Refueling Station Using Genetic Algorithms" Hydrogen 6, no. 4: 98. https://doi.org/10.3390/hydrogen6040098
APA StyleVizza, D., Caponi, R., Di Matteo, U., & Bocci, E. (2025). Cost-Optimal Design of a Stand-Alone PV-Driven Hydrogen Production and Refueling Station Using Genetic Algorithms. Hydrogen, 6(4), 98. https://doi.org/10.3390/hydrogen6040098







