Computational Fluid Dynamic Modeling and Parametric Optimization of Hydrogen Adsorption in Stationary Hydrogen Tanks
Abstract
1. Introduction
2. Computational Domain and Mathematical Formulation
2.1. Experimental Procedure Description
2.2. Governing Equation
- Hydrogen gas is considered as ideal gas;
- The mass source term, , indicates the amount of hydrogen undergoing a phase change, from the adsorbed phase to the bulk phase;
- Flow through the porous medium is described by Darcy’s law;
- No volume changes during the process;
- Local thermal equilibrium is assumed between the solid adsorbent and the gas phase;
- The flow regime is laminar.
- a
- Mass conservation
- b
- Momentum conservation
- c
- Energy Equation:
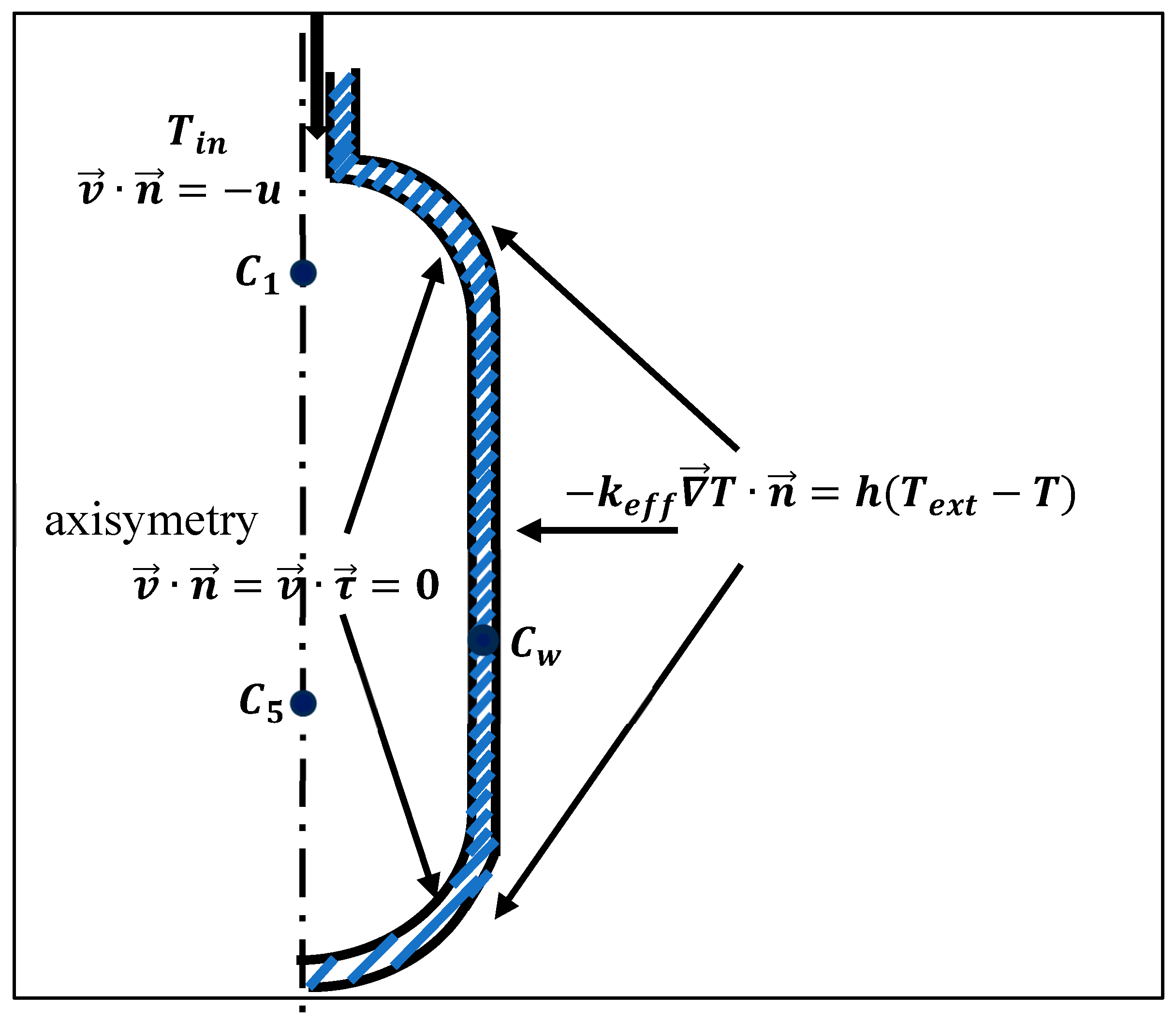
2.3. Initial and Boundary Conditions
- Fluid inlet (top boundary): Dirichlet conditions for velocity and temperature.
- Hydrogen–steel interface: Continuity of thermal flux and no-slip condition for the gas phase velocity.
- Outer cylinder: Convective heat flux boundary condition.
2.4. Modified Dubinin–Astakhov (DA) Model for Hydrogen Adsorption
- : Adsorbed amount (mol/kg);
- : Maximum adsorption capacity (saturation limit);
- : Material-specific constants (linked to adsorbent–adsorbate interactions);
- : Universal gas constant;
- Saturation pressure of .
3. Numerical Method, Grid Invariance, and Validation
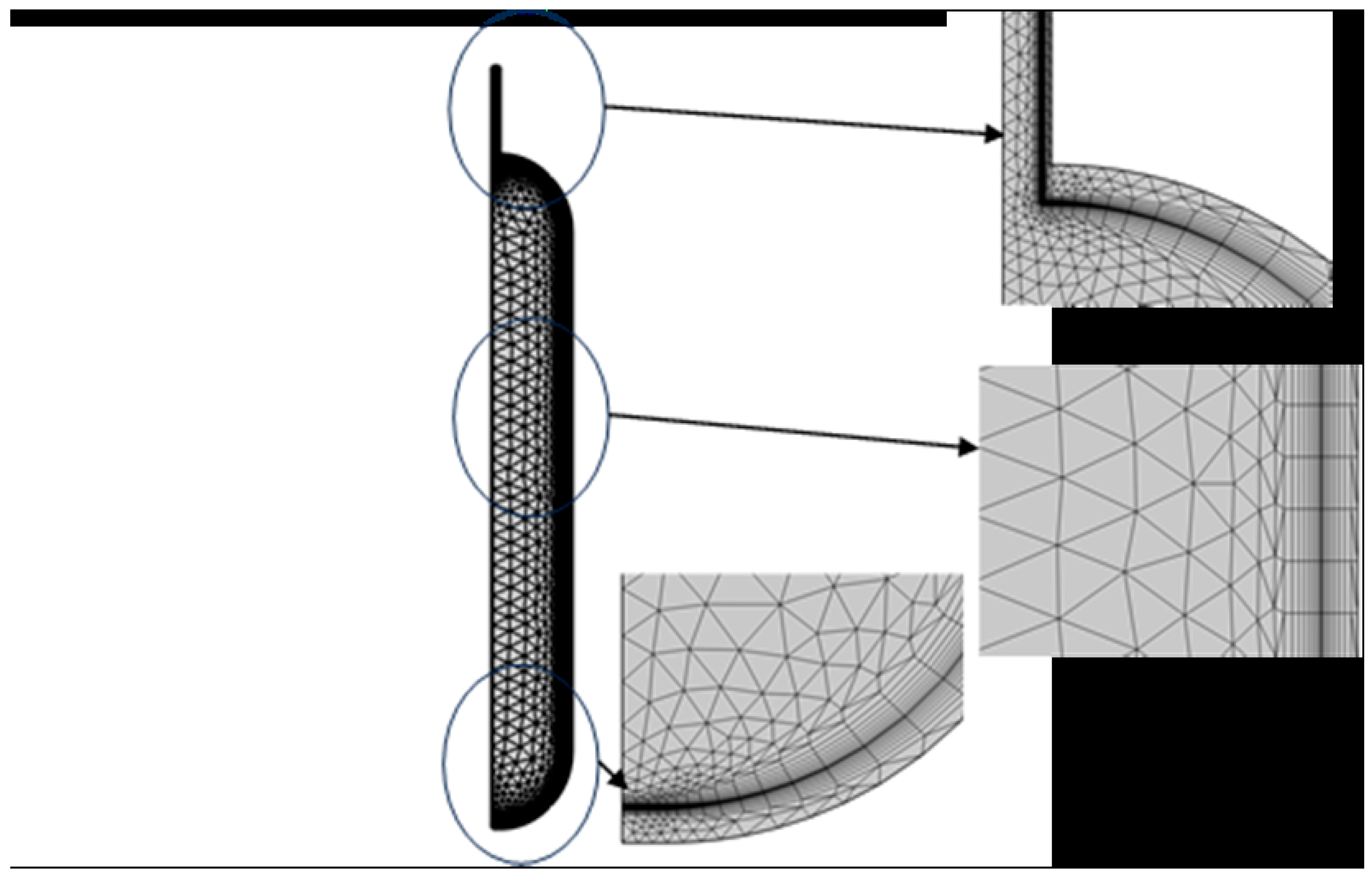
3.1. Numerical Method
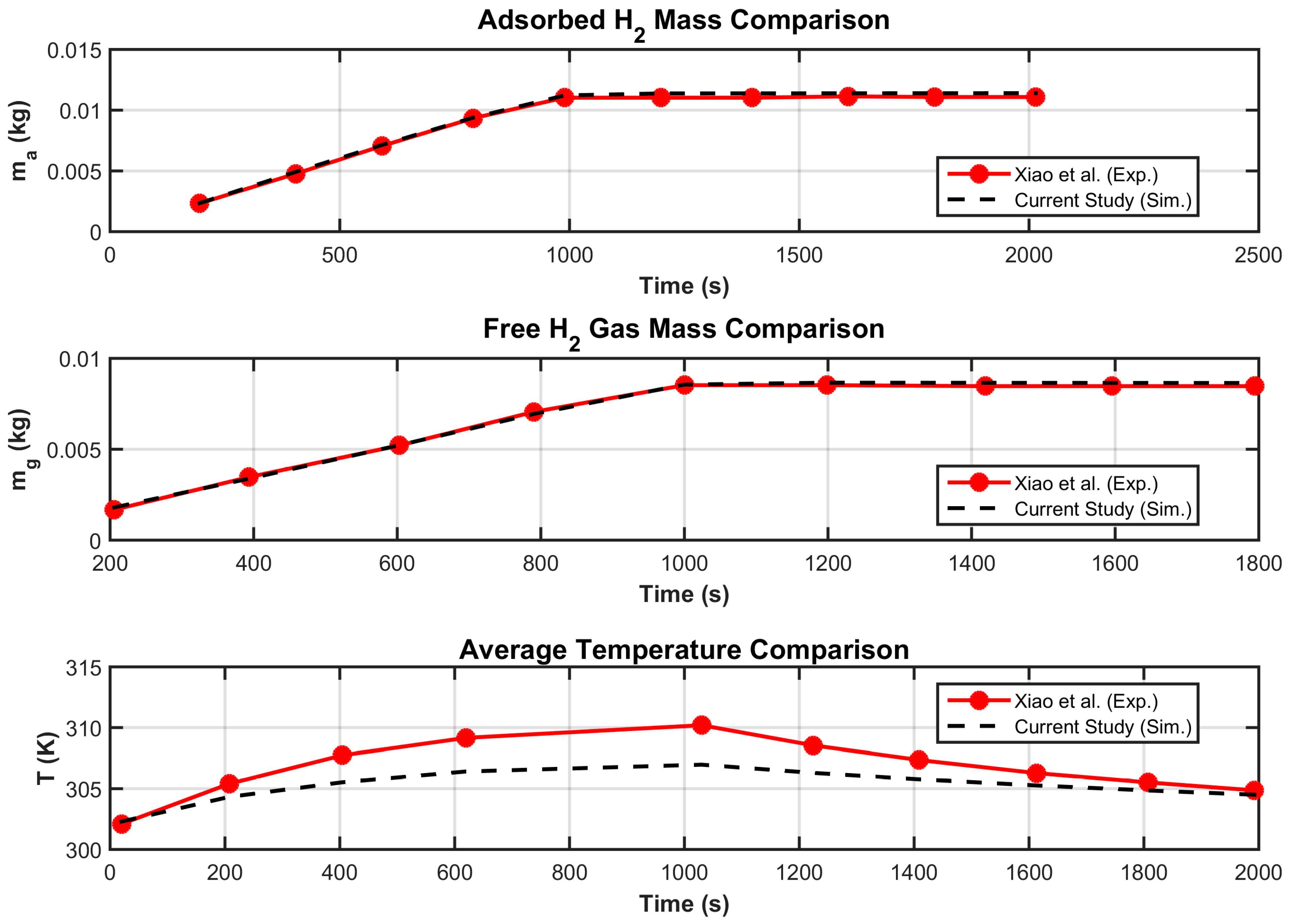
3.2. Grid Invariance and Validation
4. Parametric Study
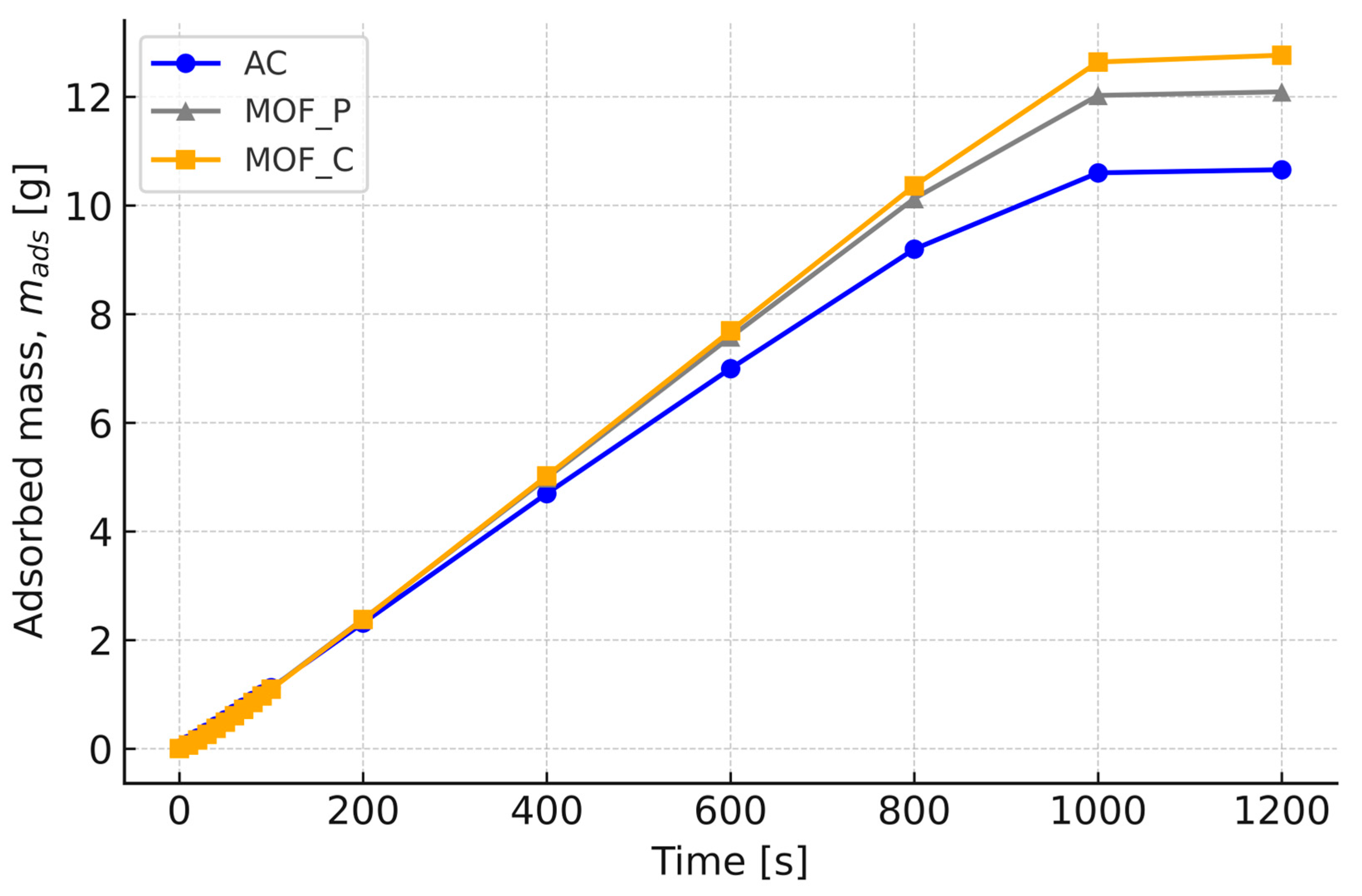
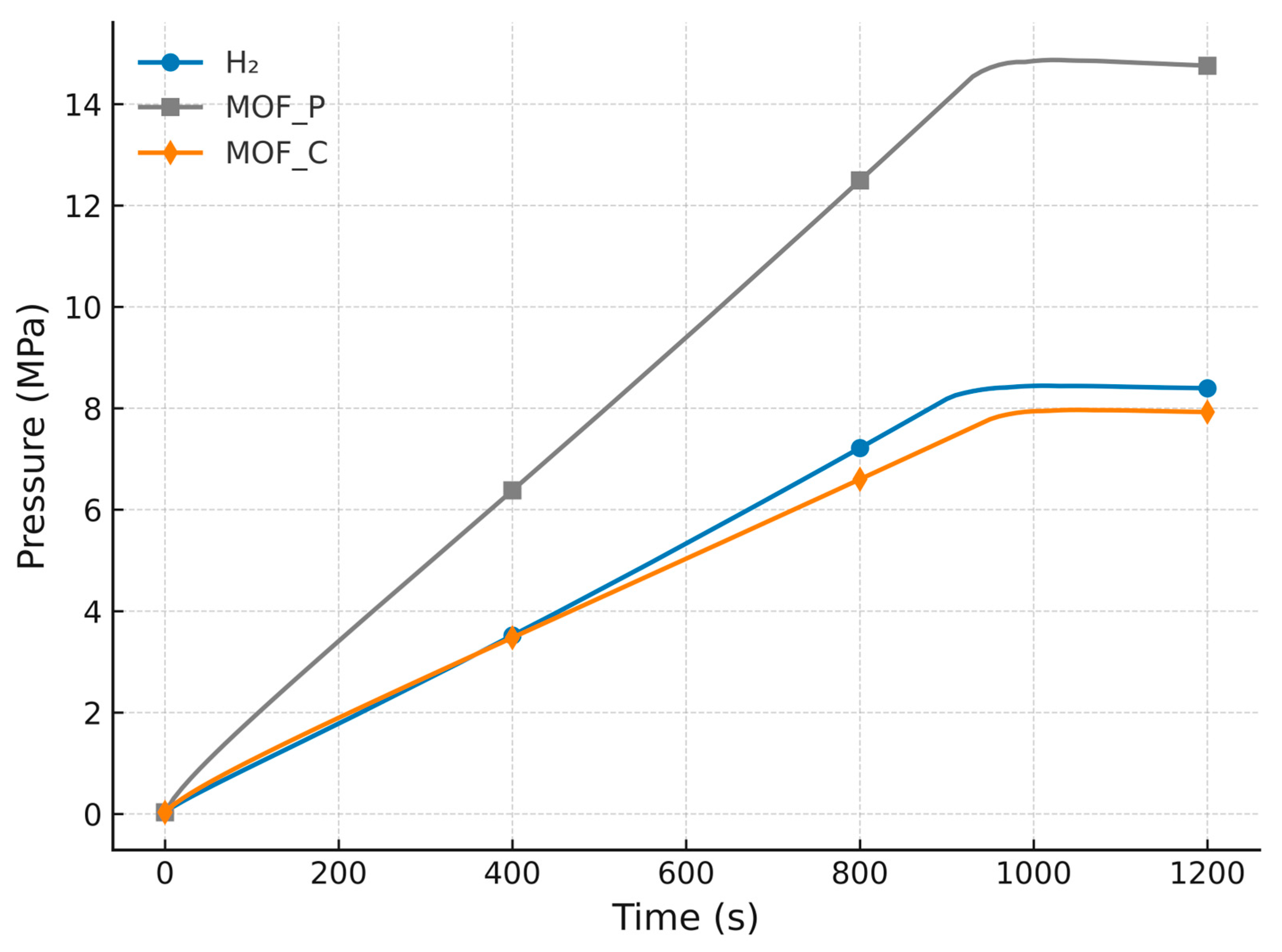
4.1. Effect of Material Properties
4.2. Effect of “Temperature and Flow Rate” Injection
5. Conclusions and Perspectives for Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| specific heat capacity | |
| particle diameter of adsorbent | |
| heat transfer coefficient | |
| thermal conductivity | |
| molecular mass of hydrogen | |
| mass of adsorbed phase hydrogen | |
| mass of gas phase hydrogen | |
| total mass of hydrogen in tank | |
| absolute adsorption amount per unit adsorbent | |
| limit adsorption amount per unit adsorbent | |
| pressure | |
| limited pressure | |
| adsorption heat | |
| universal gas constant | |
| rate, of hydrogen transfer from gas phase to adsorbed phase | |
| temperature | |
| Darcy velocity vector | |
| isosteric heat of adsorption | |
| Greek symbols | |
| enthalpic factor | |
| entropic factor | |
| density | |
| permeability of porous material | |
| dynamic viscosity | |
| bed porosity | |
| Subscript | |
| A | adsorbent |
| Ext | exterior or ambient |
| Int | initial |
| Inj | injection |
| Eff | effective |
| P | particles |
| G | gas phase |
References
- Arsad, A.Z.; Hannan, M.A.; Al-Shetwi, A.Q.; Begum, R.A.; Hossain, M.J.; Ker, P.J.; Mahlia, T.I. Hydrogen electrolyser technologies and their modelling for sustainable energy production: A comprehensive review and suggestions. Int. J. Hydrogen Energy 2023, 48, 27841–27871. [Google Scholar] [CrossRef]
- Al Ghafri, S.Z.; Munro, S.; Cardella, U.; Funke, T.; Notardonato, W.; Trusler, J.P.M.; Leachman, J.; Span, R.; Kamiya, S.; Pearce, G.; et al. Hydrogen liquefaction: A review of the fundamental physics, engineering practice and future opportunities. Energy Environ. Sci. 2022, 15, 2690–2731. [Google Scholar] [CrossRef]
- Nalla, A.A.; Nachtane, M.; Gu, X.; El Alami, M.; Gounni, A. Advances in numerical modeling and experimental insights for hydrogen storage systems: A comprehensive and critical review. J. Energy Storage 2025, 128, 117206. [Google Scholar] [CrossRef]
- Harrat, S.; Briki, C.; Sahli, M.; Settar, A.; Chetehouna, K.; Jemni, A. Experimental investigation of the hydrogen storage capacity in LaNi3.6Al0.4Mn0.3Co0.7 alloy. Int. J. Hydrogen Energy 2024, 77, 33–39. [Google Scholar] [CrossRef]
- Chen, L.; Ting, V.P.; Zhang, Y.; Deng, S.; Li, S.; Yin, Z.; Wang, F.; Wang, X. Modeling adsorption-based hydrogen storage in nanoporous activated carbon beds at moderate temperature and pressure. Int. J. Hydrogen Energy 2025, 122, 159–179. [Google Scholar] [CrossRef]
- Zeleňák, V.; Saldan, I. Factors affecting hydrogen adsorption in metal-organic frameworks: A short review. Nanomaterials 2021, 11, 1638. [Google Scholar] [PubMed]
- Umar, A.A.; Hossain, M.M. Hydrogen storage via adsorption: A review of recent advances and challenges. Fuel 2025, 387, 134273. [Google Scholar] [CrossRef]
- Chibani, A.; Boucetta, C.; Haddad, M.A.N.; Merouani, S.; Adjel, S.; Merabet, S.; Laidoudi, H.; Bougriou, C. Effect of fin material type and reactor inclination angle on hydrogen adsorption process in large-scale activated carbon-based heat storage system. J. Energy Storage 2024, 98, 113091. [Google Scholar] [CrossRef]
- Yao, J.; Zhu, P.; Guo, L.; Duan, L.; Zhang, Z.; Kurko, S.; Wu, Z. A continuous hydrogen absorption/desorption model for metal hydride reactor coupled with PCM as heat management and its application in the fuel cell power system. Int. J. Hydrogen Energy 2020, 45, 28087–28099. [Google Scholar] [CrossRef]
- Ye, Y.; Ding, J.; Wang, W.; Yan, J. The storage performance of metal hydride hydrogen storage tanks with reaction heat recovery by phase change materials. Appl. Energy 2021, 299, 117255. [Google Scholar] [CrossRef]
- Wang, J.; Melideo, D.; Ferrari, L.; Pardelli, P.T.; Desideri, U. Study on the influence mechanism of fin structure on the filling performance of cold adsorption hydrogen storage tank. Int. J. Hydrogen Energy 2024, 94, 897–911. [Google Scholar] [CrossRef]
- Huang, X.; Jin, S.; Yu, M.; Li, Y.; Li, M.; Chen, J. Numerical studies of a new device for a cryo-adsorption hydrogen storage system. Int. J. Hydrogen Energy 2024, 82, 1051–1059. [Google Scholar] [CrossRef]
- Peng, C.; Long, R.; Liu, Z.; Liu, W. Improving adsorption hydrogen storage performance via triply periodic minimal surface structures with uniform and gradient porosities. Int. J. Hydrogen Energy 2024, 53, 422–433. [Google Scholar] [CrossRef]
- Briki, C.; Dunikov, D.; Almoneef, M.M.; Romanov, I.; Kazakov, A.; Mbarek, M.; Abdelmajid, J. Experimental and Theoretical Studies of Hydrogen Storage in LaNi4.4Al0.3Fe0.3 Hydride Bed. Materials 2023, 16, 5425. [Google Scholar] [CrossRef]
- Elkhatib, R.; Louahlia, H. Metal hydride cylindrical tank for energy hydrogen storage: Experimental and computational modeling investigations. Appl. Therm. Eng. 2023, 30, 120756. [Google Scholar] [CrossRef]
- Shabbani, H.J.K.; Abd, A.A.; Hasan, M.M.; Helwani, Z.; Kim, J.; Othman, M.R. Effect of thermal dynamics and column geometry of pressure swing adsorption on hydrogen production from natural gas reforming. Gas Sci. Eng. 2023, 116, 205047. [Google Scholar] [CrossRef]
- Mahmoodi, F.; Rahimi, R. Experimental and numerical investigating a new configured thermal coupling between metal hydride tank and PEM fuel cell using heat pipes. Appl. Therm. Eng. 2020, 178, 115490. [Google Scholar] [CrossRef]
- Xiao, J.; Hu, M.; Cossement, D.; Bénard, P.; Chahine, R. Finite element simulation for charge–discharge cycle of cryo-adsorptive hydrogen storage on activated carbon. Int. J. Hydrogen Energy 2012, 37, 12947–12959. [Google Scholar] [CrossRef]
- Xiao, J.; Peng, R.; Cossement, D.; Bénard, P.; Chahine, R. CFD model for charge and discharge cycle of adsorptive hydrogen storage on activated carbon. Int. J. Hydrogen Energy 2013, 38, 1450–1459. [Google Scholar] [CrossRef]
- Xiao, J.; Peng, R.; Cossement, D.; Bénard, P.; Chahine, R. Heat and mass transfer and fluid flow in cryo-adsorptive hydrogen storage system. Int. J. Hydrogen Energy 2013, 38, 10871–10879. [Google Scholar] [CrossRef]
- Melideo, D.; Ferrari, L.; Pardelli, P.T. CFD simulation of hydrogen storage: Adsorption dynamics and thermal management in cryogenic tanks. Int. J. Hydrogen Energy 2025, 179, 149261. [Google Scholar] [CrossRef]
- Klepp, G. Modelling activated carbon hydrogen storage tanks using machine learning models. Energy 2024, 306, 132318. [Google Scholar] [CrossRef]
- Wang, C.-S.; Brinkerhoff, J. Low-cost lumped parameter modelling of hydrogen storage in solid-state materials. Energy Convers. Manag. 2022, 251, 115005. [Google Scholar] [CrossRef]
- Xiao, J.; Li, Q.; Cossement, D.; Bénard, P.; Chahine, R. Lumped parameter simulation for charge-discharge cycle of cryo-adsorptive hydrogen storage system. Int. J. Hydrogen Energy 2012, 37, 13400–13408. [Google Scholar] [CrossRef]
- Singh, A.; Maiya, M.P.; Murthy, S.S. Effects of heat exchanger design on the performance of a solid state hydrogen storage device. Int. J. Hydrogen Energy 2015, 40, 9733–9746. [Google Scholar] [CrossRef]
- Wang, J.; Melideo, D.; Ferrari, L.; Pardelli, P.T.; Desideri, U. Integrated targeted pre-cooling tubes and fins for enhanced hydrogen adsorption in activated carbon storage tank. Int. J. Hydrogen Energy 2025, 146, 149942. [Google Scholar] [CrossRef]
- Arslan, B.; Ilbas, M.; Celik, S. Experimental analysis of hydrogen storage performance of a LaNi5–H2 reactor with phase change materials. Int. J. Hydrogen Energy 2023, 48, 6010–6022. [Google Scholar] [CrossRef]
- Richard, M.A.; Cossement, D.; Chandonia, P.A.; Chahine, R.; Mori, D.; Hirose, K. Preliminary evaluation of the performance of an adsorption-based hydrogen storage system. AIChE J. 2009, 55, 2985–2996. [Google Scholar] [CrossRef]
- Nicolas, V.; Sdanghi, G.; Mozet, K.; Schaefer, S.; Maranzana, G.; Celzard, A.; Fierro, V. Numerical simulation of a thermally driven hydrogen compressor as a performance optimization tool. Appl. Energy 2022, 323, 119628. [Google Scholar] [CrossRef]
- Lopez, L.J.; Morales-Ospino, R.; Castro-Gutiérrez, J.; Sumbhaniya, H.O.; Sdanghi, G.; Dalí, S.G.; Celzard, A.; Fierro, V. Boosting hydrogen storage and release in MOF-5/graphite hybrids via in situ synthesis. Int. J. Hydrogen Energy 2025, 173, 151272. [Google Scholar] [CrossRef]
- Richard, M.A.; Bénard, P.; Chahine, R. Gas adsorption process in activated carbon over a wide temperature range above the critical point. Part 1: Modified Dubinin-Astakhov model. Adsorption 2009, 15, 43–51. [Google Scholar] [CrossRef]
- Xiao, J.; Hu, M.; Bénard, P.; Chahine, R. Simulation of hydrogen storage tank packed with metal-organic framework. Int. J. Hydrogen Energy 2013, 38, 13000–13010. [Google Scholar] [CrossRef]

| Properties | Activated Carbon | Powder MOF-5 | Compact MOF-5 |
|---|---|---|---|
| Particle density | |||
| Specific heat | |||
| Conductivity | |||
| Bed porosity | |||
| Particle diameter |
| Adsorbents | ||||
|---|---|---|---|---|
| Activated carbon (AC) | ||||
| Powder MOF-5 | ||||
| Compact MOF-5 |
| Parameter | Value/Description |
|---|---|
| Initial temperature (T0) | 302 K |
| Total mass of injection | 19.5 g |
| Ambient temperature Text | 302 K |
| Injection time | 953 s |
| Wall heat transfer coefficient | 36 W/m/K |
| Parameter | RMSE 1 | MAPE 2 | Maximum Relative Error |
|---|---|---|---|
| 2.4 × 10−4 | 2.16% | 3.24% | |
| 1.3 × 10−4 | 2.25% | 7.58% | |
| 1.82 | 0.15% | 0.10% | |
| 0.19 | 2.34% | 4.42% | |
| 2.174 | 0.54% | 1.4% | |
| 8.83 | 2.09% | 4.63% | |
| 1.019 | 0.30% | 0.46% |
| 273 | 200 | 0.012432268 |
| 273 | 400 | 0.012307034 |
| 273 | 600 | 0.012111843 |
| 273 | 800 | 0.012433435 |
| 273 | 1000 | 0.012316264 |
| 283 | 200 | 0.012410988 |
| 283 | 400 | 0.01228127 |
| 283 | 600 | 0.012130479 |
| 283 | 800 | 0.012249503 |
| 283 | 1000 | 0.012319771 |
| 293 | 200 | 0.012124952 |
| 293 | 400 | 0.012293844 |
| 293 | 600 | 0.012233828 |
| 293 | 800 | 0.012309072 |
| 293 | 1000 | 0.012339576 |
| 303 | 200 | 0.012392542 |
| 303 | 400 | 0.012196179 |
| 303 | 600 | 0.012094533 |
| 303 | 800 | 0.012031741 |
| 303 | 1000 | 0.012418507 |
| 313 | 200 | 0.012078094 |
| 313 | 400 | 0.012354711 |
| 313 | 600 | 0.012225714 |
| 313 | 800 | 0.012286743 |
| 313 | 1000 | 0.012346961 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ousegui, A.; Marcos, B. Computational Fluid Dynamic Modeling and Parametric Optimization of Hydrogen Adsorption in Stationary Hydrogen Tanks. Hydrogen 2025, 6, 95. https://doi.org/10.3390/hydrogen6040095
Ousegui A, Marcos B. Computational Fluid Dynamic Modeling and Parametric Optimization of Hydrogen Adsorption in Stationary Hydrogen Tanks. Hydrogen. 2025; 6(4):95. https://doi.org/10.3390/hydrogen6040095
Chicago/Turabian StyleOusegui, A., and B. Marcos. 2025. "Computational Fluid Dynamic Modeling and Parametric Optimization of Hydrogen Adsorption in Stationary Hydrogen Tanks" Hydrogen 6, no. 4: 95. https://doi.org/10.3390/hydrogen6040095
APA StyleOusegui, A., & Marcos, B. (2025). Computational Fluid Dynamic Modeling and Parametric Optimization of Hydrogen Adsorption in Stationary Hydrogen Tanks. Hydrogen, 6(4), 95. https://doi.org/10.3390/hydrogen6040095






