Hydrogen Safety by Design: Exclusion of Flame Blow-Out from a TPRD

Abstract

Onboard hydrogen storage tanks are currently fitted with thermally activated pressure relief devices (TPRDs), enabling hydrogen to blowdown in the event of fire. For release diameters below the critical diameter, the flame from the TPRD may blow-out during a pressure drop. Flame blow-outs pose a safety concern for an indoor or covered environment, e.g., a garage or carpark, where hydrogen can accumulate and deflagrate. This study describes the application of a validated computational fluid dynamics (CFD) model to simulate the dynamic flame behaviour from a TPRD designed to exclude its blow-out. The dynamic behaviour replicates a real scenario. Flame behaviour during tank blowdown through two TPRDs with different nozzle geometries is presented. Simulations confirm flame blow-out for a single-diameter TPRD of 0.5 mm during tank blowdown, while the double-diameter nozzle successfully excludes flame blow-out. The pressure at which the flame blow-out process is initiated during blowdown through a single-diameter nozzle was predicted.

1. Introduction

Hydrogen is mostly stored as a high-pressure gas in onboard vehicle tanks. The tanks are fitted with thermally activated pressure relief devices (TPRDs) through which the hydrogen vents in the event of a fire. The safe use of hydrogen vehicles in confined and covered spaces such as hydrogen storage enclosures on trains, maritime vessels, and planes, as well as car parks, tunnels, maintenance shops and garages, has been the topic of recent investigations [1,2].

The dimensionless correlation described in [3] demonstrated that for a given tank pressure, there is a clear relationship between the diameter of the TPRD and length of the flame. TPRD nozzle diameter and shape are two factors that both influence the flame length and width. For example, if hydrogen releases through a TPRD with the diameter of 5.08 mm at 29.6 MPa, the resultant flame would be 10.6 m, which has clear safety implications [4]. Large TPRD diameters not only lead to unacceptable flame lengths, but also increase the risk of a pressure peaking phenomenon (PPP) in confined spaces. Previous work [5,6] has indicated that TPRD diameters should be kept as small as possible, ideally of the order of 0.5 mm to avoid excessive overpressure because of the pressure peaking phenomena when the tank vents in an enclosed space with limited vent size. A small diameter TPRD orifice reduces the mass flow rate during blowdown, thus avoiding the potential for pressure peaking to occur. On the other hand, TPRD diameters less than 1 mm could introduce the potential for flame blow-out as discussed in the authors’ previous study [7]. Therefore, it should be underlined that the reduction in the TPRD diameter to avoid the pressure peaking phenomenon must be accompanied by the analysis of the tank’s fire resistance to exclude its rupture in a fire [8,9,10] and the potential of flame self-extinction, i.e., blow-out, during pressure drop in the compressed hydrogen storage system (CHSS) for TPRD diameters less than 1 mm. Indeed, if a blow-out occurs during a release in a confined or covered space, then there is potential for a flammable cloud to form and deflagrate or even detonate with catastrophic safety implications. An understanding of the pressure limits for hydrogen-sustained flames and the dynamic flame behaviour during blowdown is important for the inherently safer design of CHSS with TPRDs.

A detailed overview of hydrogen flame stability can be found in the work by Kazemi et al. [7] and only the key points are summarised here. Blow-out is defined by Wu et al. in 2007 [11] as an extinguishment of a lifted flame and this definition is used in this work. Different models have been proposed to explain the flame stabilisation mechanism starting with Vanquickenborne and Van Tiggelen in 1965 [12] who proposed that the flame stabilisation point is defined as the distance from the burner exit where the turbulent burning velocity of the premixed flame is equal to the mean gas velocity, and blow-out occurs when the mean gas velocity exceeds the turbulent burning velocity. Kalghatgi et al. in 1984 [13], other researchers and more recently Wang et al. in 2023 [14] have continued to investigate this phenomenon to better understand the flow parameters which influence the flame behaviour. It has been emphasized in several studies that the flame remains stable when the flame base is positioned downstream of the maximum stoichiometric waistline point of the fuel concentration in the air; otherwise, a flame blow-out occurs [15,16,17]. A key parameter for non-premixed flame stability is the critical diameter which represents the minimum nozzle size through which a free jet flame will remain stable at all driving pressures. When hydrogen is released through a nozzle where the diameter is equal to or larger than the critical diameter, and it is ignited, the resultant flame is stable regardless of the reservoir pressure. Several experimental studies have determined the critical diameter for hydrogen to be in the region of 1 mm [17,18,19]. Previous work by the authors [7] includes validation of a numerical model, which can successfully reproduce the critical diameter and stability limits for hydrogen jet flames at a constant driving pressure.

Whilst a flame will be sustained for all driving pressures when a release occurs through a diameter greater than the critical diameter, this is not the case for diameters below the critical diameter. In 2009, conditions for sustained hydrogen flame and blow-out limits were investigated by Mogi et al. [19] through a series of experiments with different nozzle diameters and release pressures. The limits separating the zones of sustained flame and flame blow-out for hydrogen are defined for low- and high-pressure limits of stable hydrogen flames. It was concluded by Mogi et al. [19] that the lower pressure limit for flame extinction was almost constant and independent of nozzle diameter, while the upper pressure limit of flame blow-out was reduced with the increase in nozzle diameter. The flame stability curve for hydrogen developed by Mogi et al. [19] has been numerically reproduced in [7]. It is this validated model [7] that is applied in this work, and the flame stability curve which is the basis of the analysis is presented here. While the work by Mogi et al. [19] demonstrated flame blow-out in certain regions for straight nozzles, a “double-diameter” nozzle design has been potential to avoid blow-out. A series of experiments performed by Henriksen et al. in 2019 [20] using a “double-diameter” nozzle geometry comprising two parts, an “upstream” smaller diameter nozzle, followed by a wider diameter “downstream” nozzle, e.g., 0.5 mm to 2 mm or 4 mm. They undertook experiments at constant release pressures and the goal of the experimental study [20] was to determine the under-expanded hydrogen flame length. However, it was demonstrated that for this “double-diameter” nozzle configuration the flame would be stable, and blow-out would not happen at pressures where a release through a 0.5 mm “single-diameter” nozzle experiences blow-out [19]. Kazemi et al. [7] simulated releases through a “double-diameter” nozzle and demonstrated a flame is sustained at constant pressures where blow-out occurs through a single-diameter nozzle with the same constant mass flow rate. The work published to date is primarily focused on observing flame behaviour at fixed (not changing in time) pressures.

There is an absence of published work, either experimental or numerical, demonstrating dynamic flame behaviour during continuous pressure reduction, which is very relevant for the practical case of blowdown from hydrogen onboard storage. This work is needed to predict how flame blow-out can be excluded during tank blowdown using a double-diameter nozzle TPRD. This replicates a real scenario. Simulating blowdown enables the pressure at which flame blow-out happens through a conventional single diameter nozzle TPRD to be predicted. It has previously been proposed in the literature [15,16,17] that a flame will be sustained if the flame edge is located upstream of the maximum stochiometric waistline point. It was proposed [15,16,17] that a flame will blow-out if the flame edge is located downstream of the maximum stochiometric waistline. Simulation of the dynamic process will enable this transition to be investigated.

2. Problem Description—Flame Stability during Pressure Blowdown

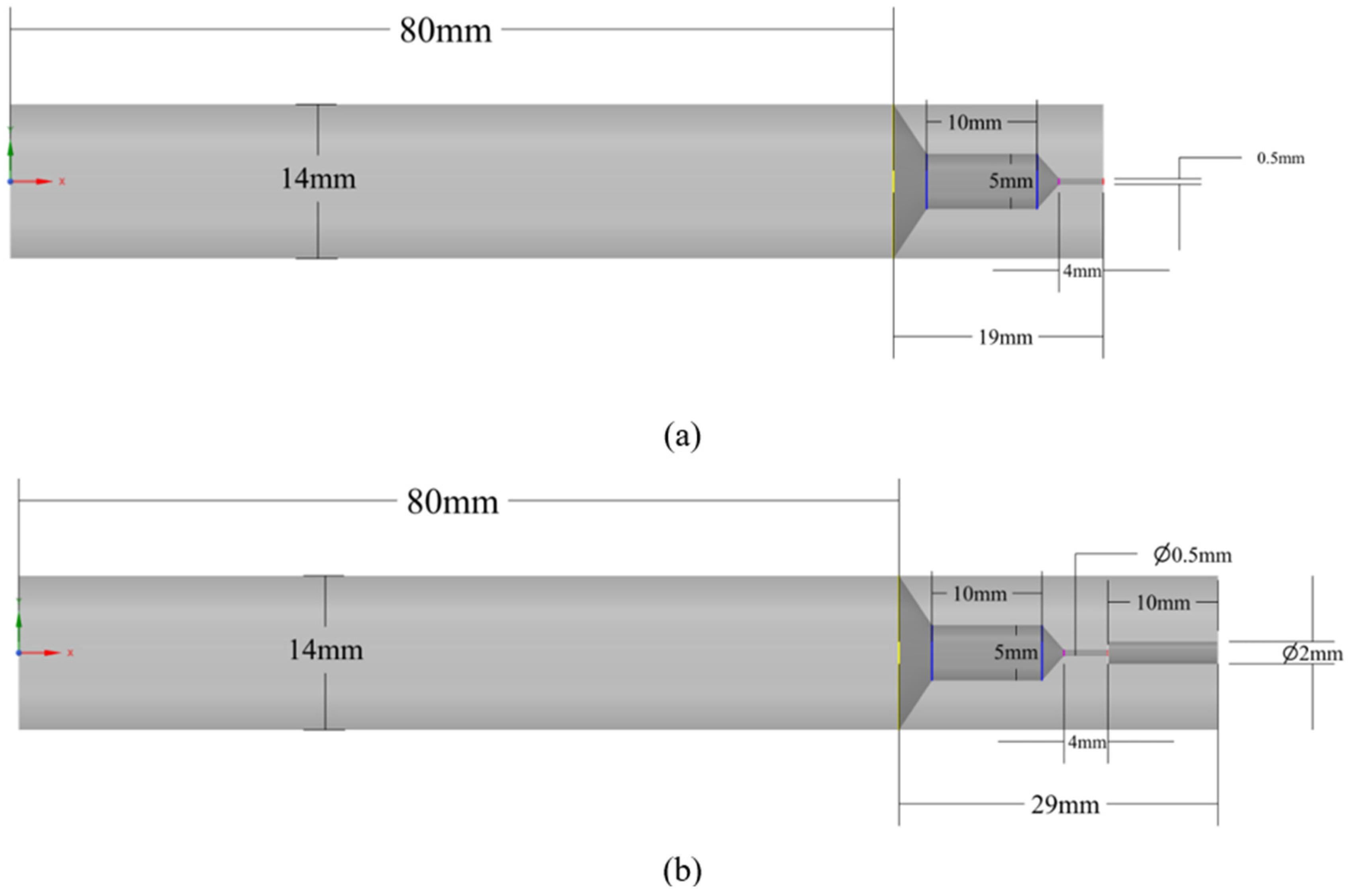
The focus of this study is to simulate the dynamic flame behaviour, including flame blow-out, during storage tank blowdown through two different designs of TPRD nozzle geometries. A schematic of the two nozzle geometries is shown in Figure 1. The first scenario considered was blowdown through a TPRD, with a typical diameter of 0.5 mm. This was compared to a second scenario of blowdown through a smart TPRD design with a “double-diameter” nozzle of an upstream 0.5 mm diameter section, followed by a downstream 2 mm diameter section. Both geometries were considered for constant pressure releases in our previous work [7].

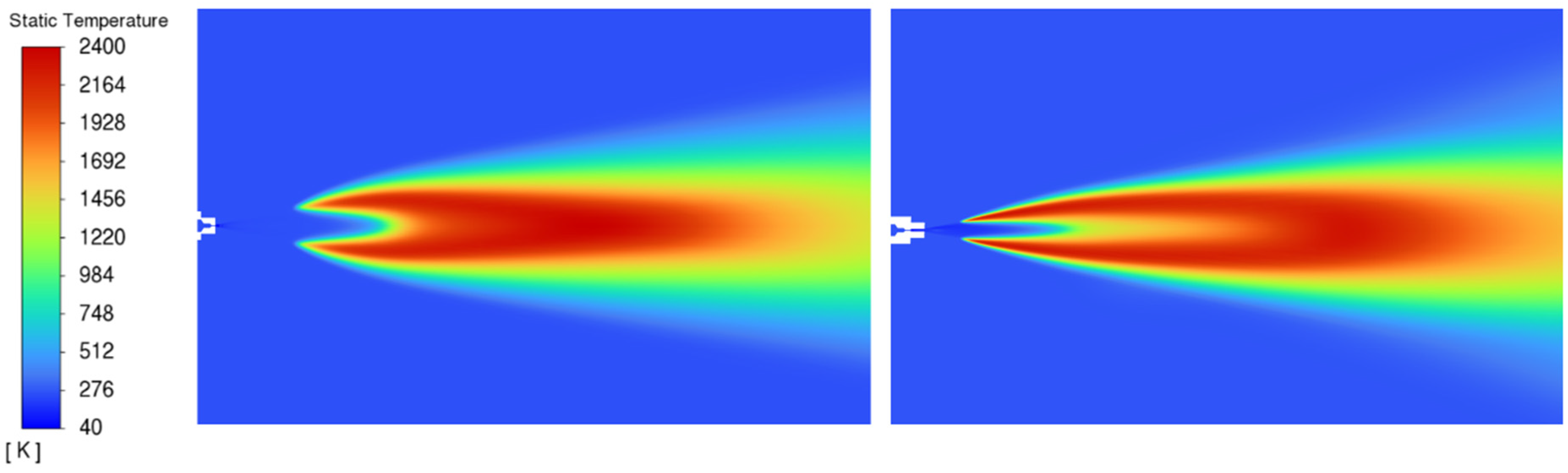
The “double-diameter” nozzle was formed from two parts, referred to as the downstream and upstream nozzles. The diameter of the upstream nozzle was 0.5 mm, which controls the mass flow rate, the dominant parameter affecting the pressure peaking phenomenon [5,6,21,22,23], and the diameter of the downstream nozzle was 2 mm (above the critical diameter for hydrogen of 1 mm), which controls the hydrogen concentration and velocity profiles, dominant parameters affecting flame blow-out. 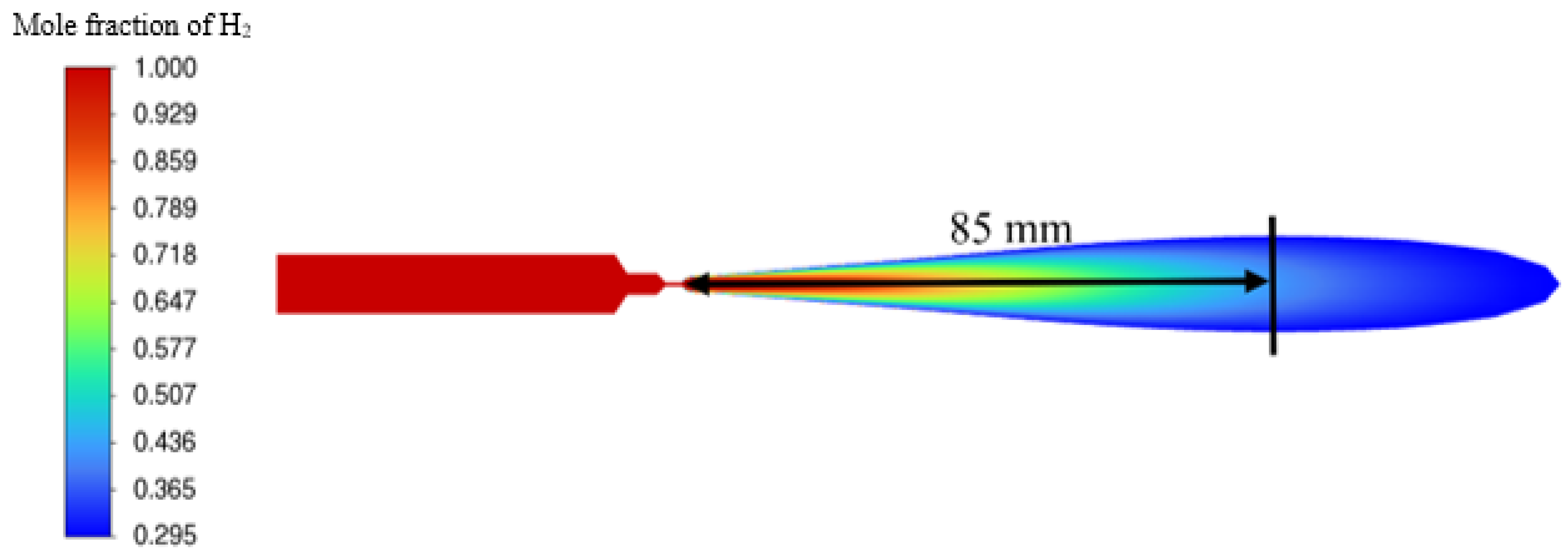It was shown previously by the authors [7] that the hydrogen concentration profile is changed (becoming wider) when the 2 mm diameter nozzle is located downstream of the 0.5 mm diameter nozzle, and consequently, the flow velocity on the elliptic stochiometric contour where the flame tip would be anchored is decreased dramatically. Hence, a stable flame forms when hydrogen is released through the “double-diameter” nozzle whereas the flame would blow out if it is released through the 0.5 mm diameter nozzle at the same driving pressure.

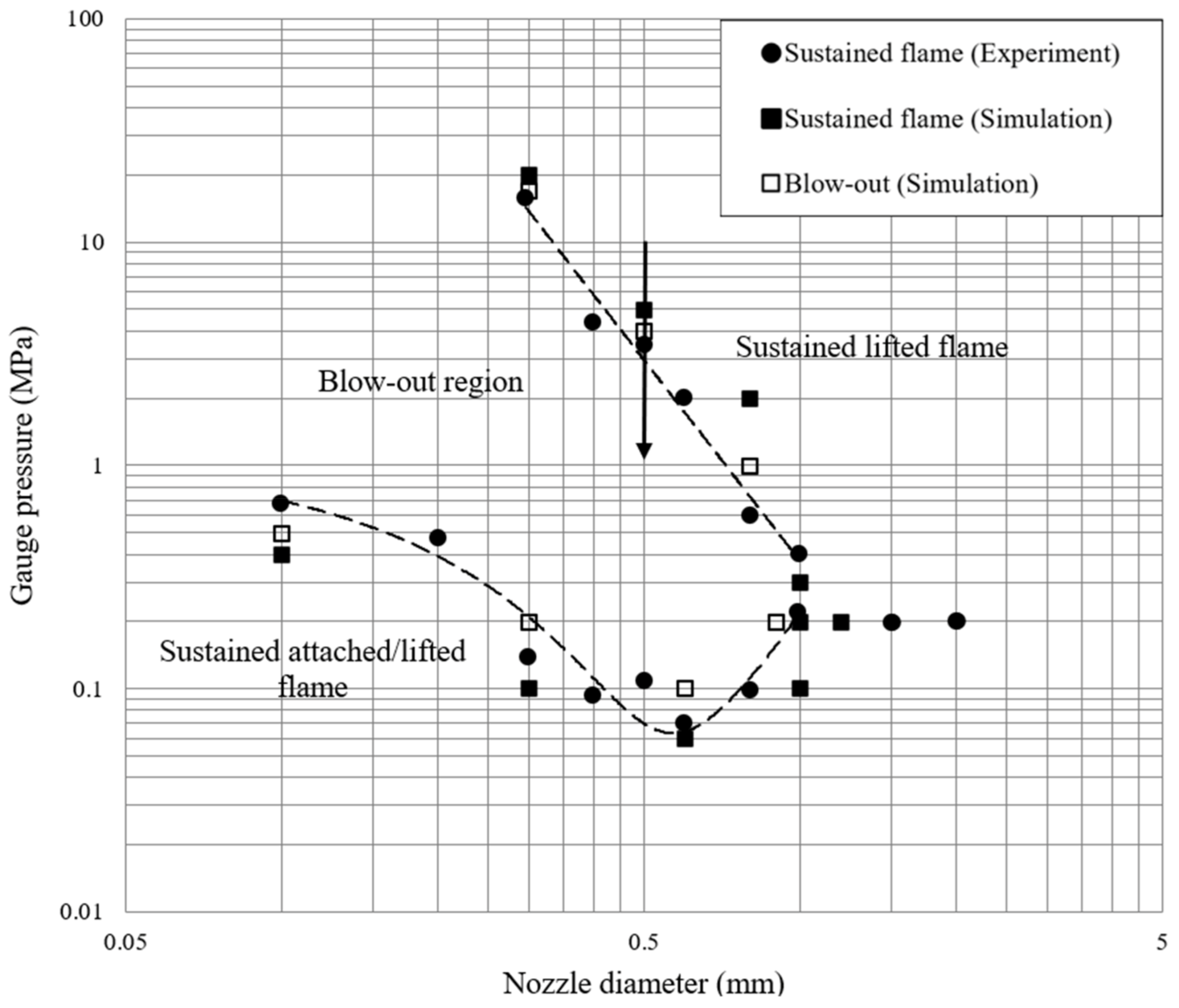
By simulating blowdown through a TPRD, the aim is to replicate a real scenario where a high-pressure hydrogen tank is close to a fire and the TPRD is activated. In this situation, hydrogen will be released and ignited to sustain a flame at higher pressures. However, as the tank blows down, the flame will pass through the upper flame stability pressure limit and is expected to blow out. The flame stability curve for hydrogen incorporating the experimental data of Mogi et al. 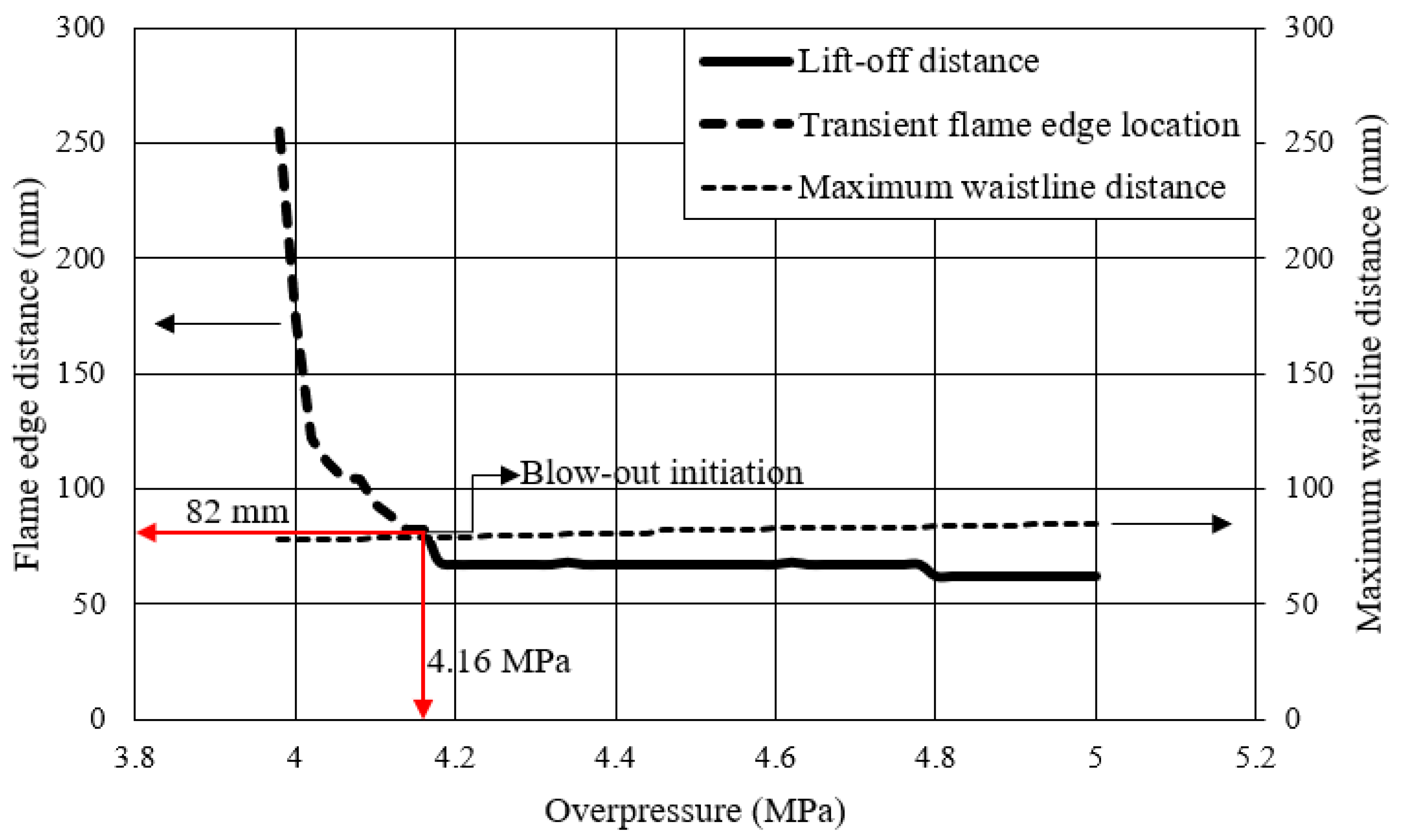[19] and simulated numerically in [7] is shown below in Figure 2 to demonstrate the region pertinent to this study. While the diameter of the TPRD is constant, the pressure is decreasing during tank blowdown. Therefore, the flame will enter the blow-out zone as the pressure decays. 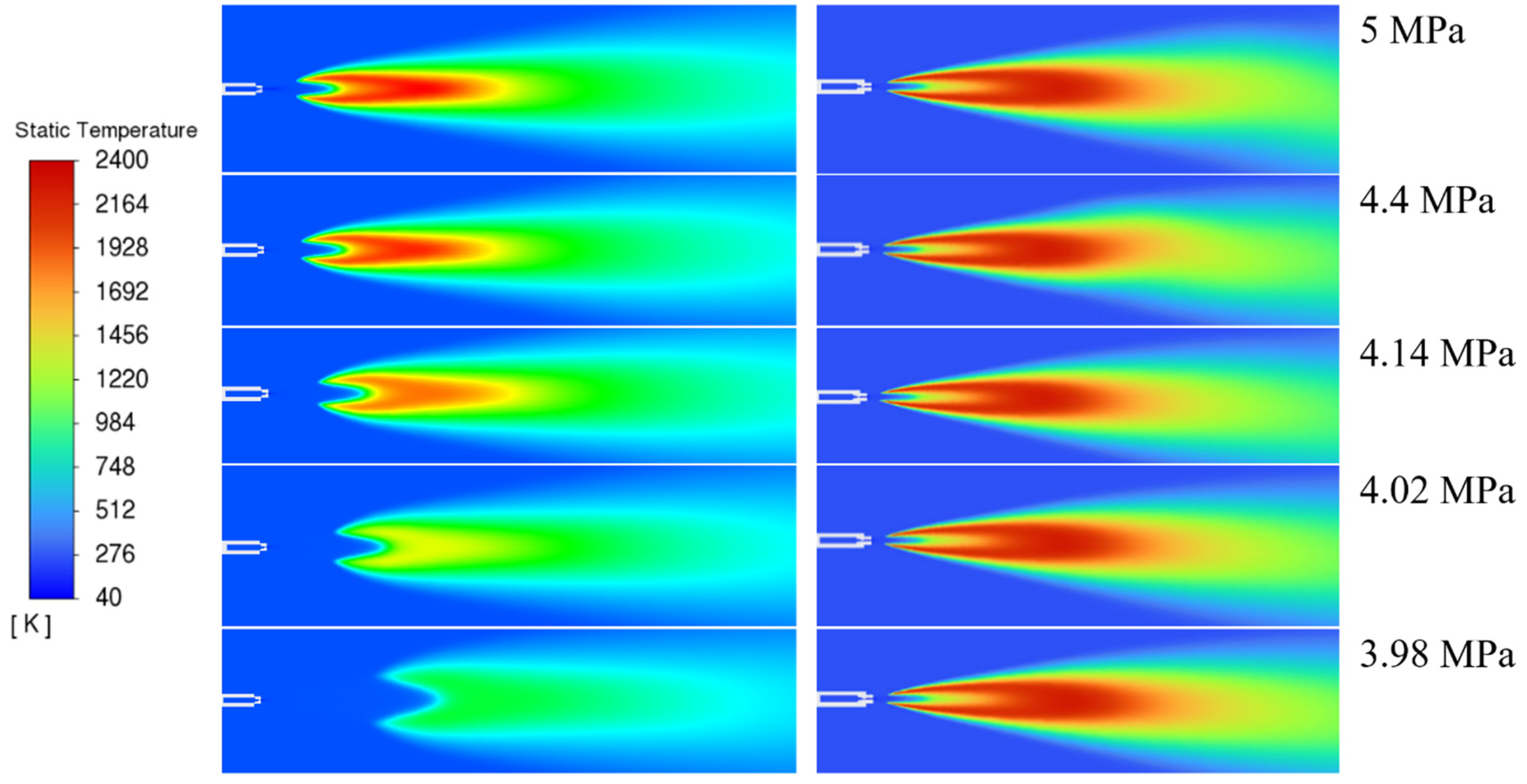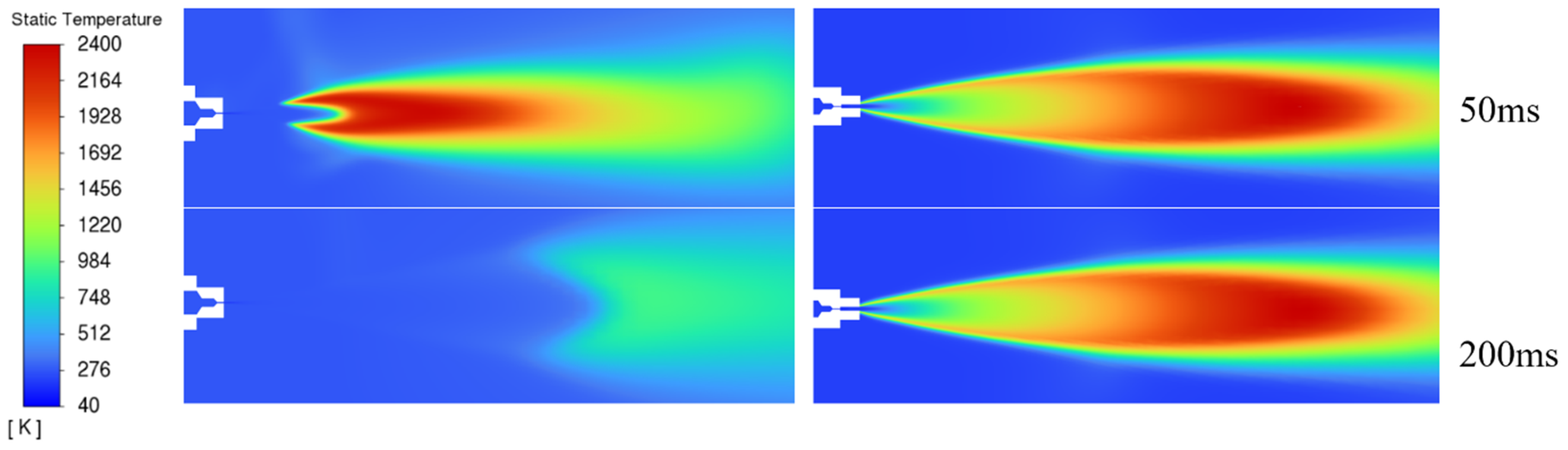The black arrow in Figure 2 represents the behaviour for blowdown through a 0.5 mm diameter nozzle. Whilst hydrogen tanks are typically at pressures of 35 to 70 MPa, blow-out is expected to occur in simulations closer to 4–5 MPa for nozzle diameters of 0.5 mm; thus, it is pressure decay around this region that is of most relevance here.

The two geometries considered here were previously examined in our work at fixed driving pressures [7]. However, in this work the pressure at which blow-out occurs for releases through a 0.5 mm diameter nozzle are also determined.

The numerical approach applied here is like that validated in previous work [7] and is described below in Section 3. The Reynolds-Averaged Navier–Stokes (RANS) based approach has been employed to model the dynamic process of flame behaviour and blow-out during the blowdown. An unignited blowdown scenario has also been simulated in order to provide insight into how the waistline position changes with decreasing pressure. 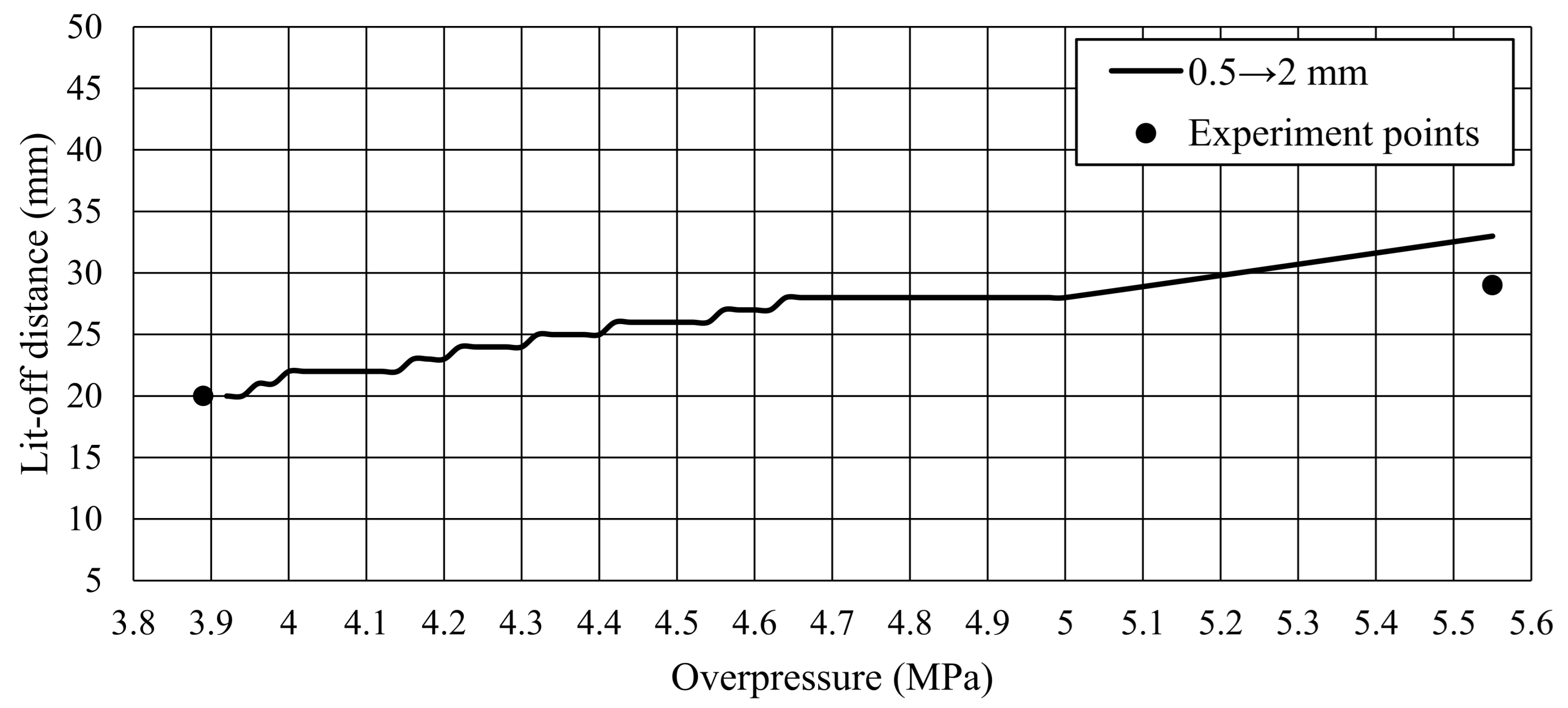Minor adaptations have been made to the validated model presented in [7] to reduce the sensitivity of flame behaviour to Sc number, these changes are described in Section 3. Results using this model are presented for releases in the region of the critical diameter. Releases through 0.9 mm and 1 mm are presented to confirm that the results align with those presented in our previous validation study [7]. Additionally, two constant-pressure hydrogen releases at 0.2 MPa and 5 MPa (gauge) through the two geometries have also been simulated to demonstrate the flame behaviour under constant pressure conditions and emphasize the clear differences in behaviour at key pressures. Results are presented in Section 5.2.

3. Model and Numerical Approach

ANSYS fluent version 2023R1 was used as a computational engine to solve the governing equations. In this study, the pressure range was lower than 10 MPa and thus real gas effects were deemed negligible. The coupled method was used for pressure–velocity coupling. A second-order upwind scheme was applied to discretise density, momentum, energy, and species transport equations. A first-order implicit scheme was used for temporal discretisation. A second-order scheme was used to interpolate pressure values at cell faces. The mass, momentum, energy, and species transport equations were solved, and a complete set of equations can be found in [7]. A single-step global chemical reaction with four species was employed for the reaction of hydrogen with air, therefore water is the only product of the combustion.

The realizable k-ε turbulence model [24], known for its capability to predict the spreading rate of axisymmetric jets [25], and previously applied for simulations of hydrogen under-expanded jet fire by Cirrone et al. [26], was employed to solve the equations governing turbulent kinetic energy (k) and dissipation rate (ε). The details of k and ε equations can be found in ANSYS fluent theory guide [25] and in our previous validation study [7]. Our previous work [7] demonstrated the sensitivity of hydrogen flame stability to the turbulent Sc number. This is undesirable if other fuels are to be considered. Thus, adaptations have been made to the model in this work, reducing the sensitivity to the Sc number and enabling the more commonly applied turbulent Sc number of 0.7 to be used. Specifically, the kinetic theory model for molecular mass diffusivity was included (Equation (1)) and dissipation due to compressibility [27], $Y_M$, was accounted for in the transport equation for turbulent kinetic energy, as follows:

$$\frac{\partial \left(\rho k\right)}{\partial t}+\frac{\partial }{\partial x_i}\left(\rho k{U}_i\right)=\frac{\partial }{\partial x_i}\left[\left(\mu +\frac{{\mu }_t }{{\sigma }_k}\right)\frac{\partial k}{\partial x_i}\right]+G_k+G_b+\rho \epsilon {+Y}_m,$$

(1)

$$Y_M=2\rho \epsilon {M_t}^2,$$

(2)

$$M_t=\sqrt{\frac{k}{a^2}}.$$

(3)

The Eddy Dissipation Concept (EDC) was applied as a finite rate model for combustion to enable the flame behaviour to be captured (either sustained flame or blow-out) [25].

4. Numerical Details

A schematic of the two nozzle geometries is given above in Figure 1. However, full details on the geometry and grid can be found in the author’s previous study [7]. The geometry of the computational domain was a cylinder with a diameter of 6 m and a length of 13 m. This was considered large enough to mitigate the effect of numerical boundaries on the flame, making it applicable to real-world applications. The grid contains 400k hexahedral cells. The nozzle was resolved with 20 cells along the diameter. The resolution of the grid in the vicinity of the nozzle was fine enough to capture the shock structure in all simulations. Grid and time step independency studies was performed previously and described in [7]. In our previous work [7], it was shown that a timestep of 10⁻⁴ s was sufficient. In the work presented here, 10⁻⁶ s was used initially until a flame was established, reduced to 10⁻⁴ s as the simulation progressed.

Simulation of blowdown or indeed a stationary point is computationally expensive in order to adequately capture the flame dynamics including resolution of the shock structure. Thus, the simulations focus on pressure decay in the region where blowdown is predicted to occur, rather than across the full pressure range. 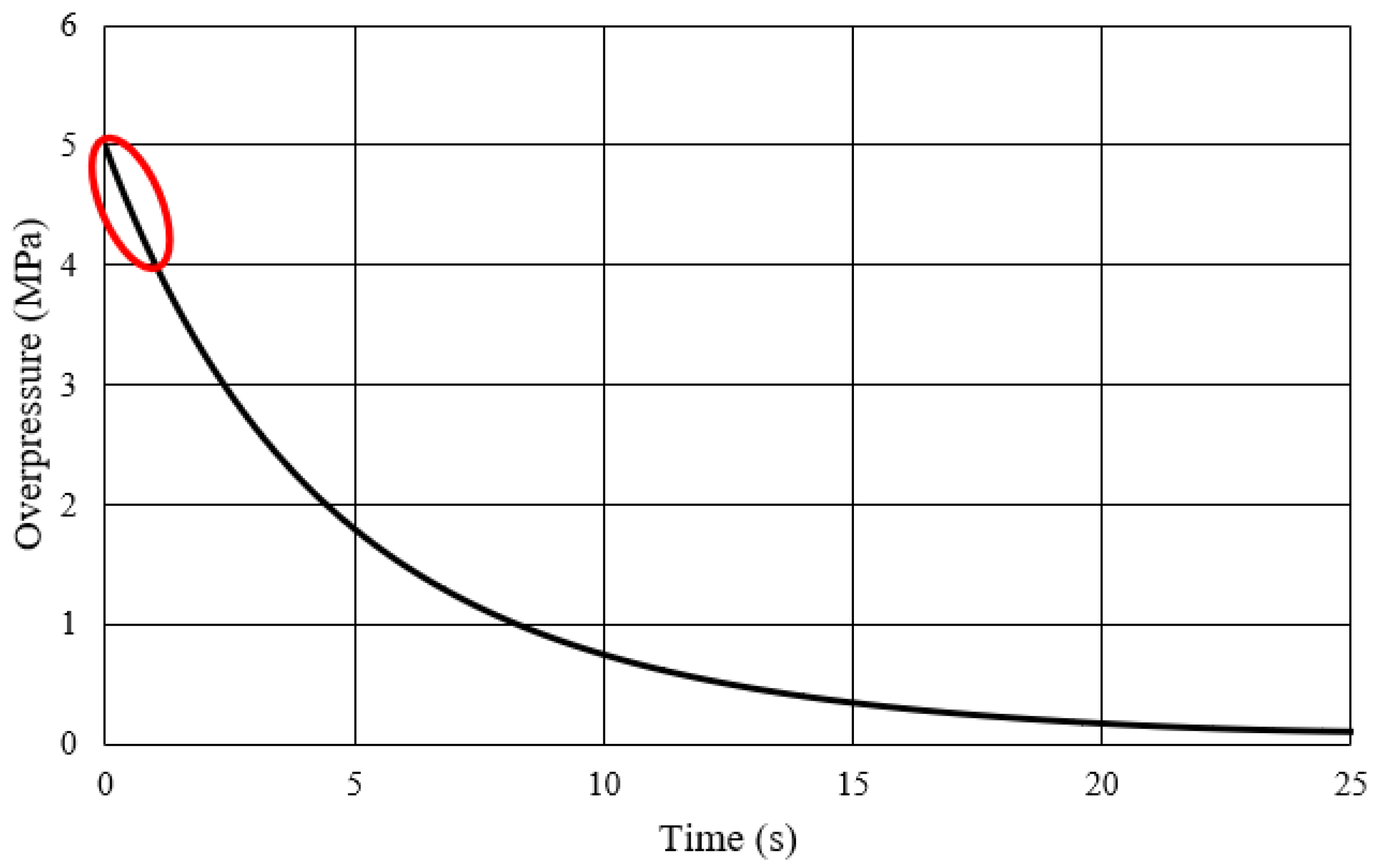The validated model for adiabatic blowdown of a storage tank was used to estimate pressure decay during blowdown from 5 MPa [28] which can be accessed as a tool in e-Laboratory of Hydrogen Safety [29]. 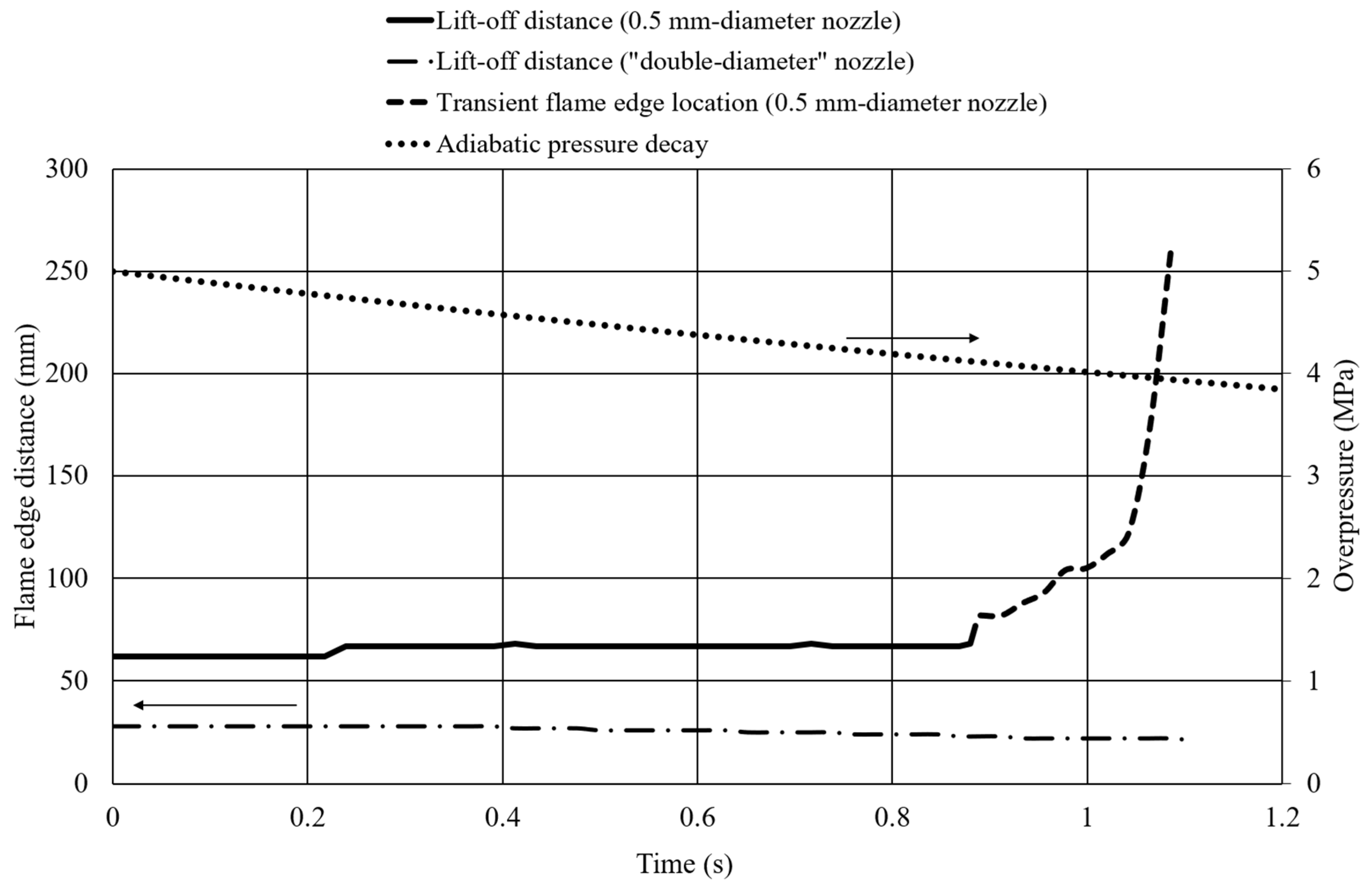The predicted pressure decay curve for blowdown from an imaginary tank of comparatively small volume 1 L, chosen to reduce simulation time, is shown in Figure 3. A larger volume was initially considered, but simulation times proved prohibitive (greater than 1 month). A polynomial based on this decay curve was used to define the hydrogen inlet boundary in the simulations:

$$P={10}^{-7}{t}^6-{10}^{-5}{t}^5+0.0004t^4-0.0091t^3+0.1259t^2-1.0843t+4.9878.$$

(4)

In our previous study [7], it was shown how for a 0.5 mm diameter, a release at a constant pressure of 5 MPa resulted in a sustained flame and a constant release at 4 MPa resulted in a flame blow-out. Therefore, it could be expected that the flame will be blown out at a pressure reduction from 5 MPa to 4 MPa; this was circled in Figure 3 as the region of interest in this study.

The temperature at the hydrogen inlet boundary was assumed to be 300 K. It was demonstrated by Schefer et al. [30], that with decreasing pressure during blowdown, temperature initially decreased, reaching a consistent level thereafter. Thus, the assumption of constant temperature at boundary conditions was considered reasonable.

Pressure boundary conditions were applied for the upstream, radial, and downstream boundaries of the calculation domain. Temperature, absolute pressure, and oxygen mass fraction were 300 K, 0.1 MPa, and 0.23, respectively. The nitrogen mass fraction is defined within fluent as 0.77. A no-slip condition was employed for all solid wall boundaries. To decrease computational cost, a steady-state solution of the unignited release was first simulated. Once the unignited jet had been established, the transient solution and combustion model were activated. The turbulence model and constants were the same for the steady-state and unsteady solutions. The pressure-based steady-state solver, the realizable k-ε; turbulence model and coupled scheme for pressure–velocity coupling were used in this initial unignited release stage. In the same approach as our previous study [7], to ignite hydrogen a static temperature of 2400 K, which is the adiabatic temperature of hydrogen flame, was patched until the flame started to propagate and water concentration could be seen to increase, demonstrating combustion is taking place.

5. Results and Discussion

As explained in Section 3, the validated CFD model proposed in [7] was modified in this study to enable its application with the generally accepted value of turbulent Schmidt number of 0.7. This section describes the application of the modified model to reproduce the critical diameter (Section 5.1). Then, the model is applied to simulate the dynamic behaviour of the flame during tank blowdown (Section 5.2).

5.1. Flame Stability and the Critical Diameter

Two constant pressure scenarios were modelled in the region of the critical diameter, specifically, diameters of 0.9 mm and 1 mm at a driving pressure of 0.2 MPa. At 0.9 mm flame blow-out was observed and at 1 mm a sustained flame was predicted. Temperature contours for both scenarios are shown in Figure 4 for the first 300 ms of the ignited release. Figure 4a demonstrates a numerical blow-out. For the 0.9 mm nozzle diameter scenario, the temperature in the jet reduced with time and the hot products moved downstream and out of the domain; combustion was not maintained. In contrast, a sustained flame could be observed in Figure 4b for the 1 mm nozzle diameter scenario. A flame developed and reached a quasi-steady state. Thus, the model successfully reproduced the experimentally defined critical diameter for the hydrogen flame by Mogi and Horiguchi [19], and the results aligned with those presented in our previous work [7].

5.2. Dynamic Flame Stability Behaviour during Blowdown

The process of transition from sustained flame to blow-out was observed during blowdown through a 0.5 mm diameter nozzle. In contrast, no blow-out was observed during blowdown through the “double-diameter” nozzle geometry in previous work [7]. It should be emphasised that the mass flow rate through both geometries was the same; however, the flow velocity differed and hence impacted flame stability, as discussed in Kazemi et al. [7].

As depicted in Figure 5, during blowdown through the 0.5 mm diameter nozzle (the red arrow pointing to the left indicates time of the blowdown progress), blow-out was predicted to start occurring in the region between 4.16 MPa and 3.98 MPa, at which point the flame edge distance (the distance between the flame edge and nozzle exit) began to exceed the axial distance from the nozzle to location of maximum stoichiometric hydrogen concentration waistline. The change in flame edge location with pressure decrease during blowdown is shown in Figure 5. The maximum stoichiometric waistline axial location based on an unignited blowdown scenario is also shown in Figure 5. The thick solid line in Figure 5 shows the lift-off distance for steady flame scenarios when it was below the maximum waistline distance. The flame blew out when the lift-off distance became equal to or exceeded the maximum waistline location. This happened when the pressure in this 1-L tank dropped to 4.16 MPa, at which pressure the maximum stoichiometric waistline distance was 79 mm, while the flame edge location was 82 mm. The transient location of the flame edge for the unsteady flame which was blowing out during blowdown, is shown by the dashed line in Figure 5. It is important to note, when interpreting Figure 5, that overpressure decreases with time during tank blowdown; i.e., moving from right to left in the figure corresponds to decreasing time.

As an example, the elliptic contour of hydrogen stochiometric concentration in air and the maximum waistline position at 5 MPa are shown in Figure 6.

Based on an interpretation of the experiments performed by Mogi and Horiguchi [19] the lowest pressure (gauge) to support a sustained flame is in the region of 3.5 MPa (this represents a difference of approximately 18% with simulations). However, it should be noted that experiments were performed at a constant driving pressure.

The flame lift-off height change (decrease in this scenario) with a decrease in pressure during blowdown through the “double-diameter” nozzle is shown in Figure 7. Whilst the lift-off height reduced with decreasing pressure in line with behaviour observed experimentally by Henriksen [20], it should be noted that this was across a relatively narrow range and was in line with two experimentally determined values also shown on the graph [20].

Figure 5 illustrates the lift-off distance for steady flame scenarios when the flame edge distance is shorter than the maximum waistline location and the transient location of the flame edge for the unsteady flame, which is blowing out during blowdown. Figure 7 represents the lift-off distance as it changes with pressure for the “double-diameter” nozzle. This behaviour for both nozzle geometries is in line with that observed for steady state releases too and thus could be considered applicable for blowdown from a range of tank volumes. It should be noted that the data presented in Figure 8 are based on a tank volume (1 L) considered in this work, so the blowdown time will vary with tank volume. Figure 8 describes the change in flame edge distances for both TPRD designs and overpressure with respect to time. Blow-out can be seen to occur for the 0.5 mm diameter nozzle after approximately 0.9 s of the release, where the flame edge distance rapidly increases.

Temperature contours during blowdown are shown for both nozzle geometries in Figure 9 for decreasing pressure. Both geometries are shown side by side for comparison of flamed behaviour as pressure reduces in each case. It can be seen how the hot products begin to propagate away from the standard 0.5 mm nozzle during blowdown, and combustion is no longer sustained. In contrast, the flame behaviour remains relatively constant for the “double-diameter” nozzle despite the driving pressure dropping.

Figure 9 is focused on the dynamic flame behaviour as the pressure blows down over the range 5–4 MPa. Constant pressure simulations for both nozzle geometries were also carried out to demonstrate the clear differences in behaviour at key pressures. Specifically, this was at 5 MPa where a sustained flame could be expected for both geometries, and 0.2 MPa, the pressure which corresponded to the region where the blow-out zone covered the widest range of diameters (shown earlier in Figure 2). Temperature contours for both geometries are given for 5 MPa in Figure 10 and 0.2 MPa in Figure 11. A sustained flame can be seen for the “double-diameter” nozzle in both cases, but the 0.2 MPa is the most significant, indicating the impact on flame stability.

This work demonstrated the dynamic flame behaviour of hydrogen during tank blowdown for the first time. This has implications for existing designs of TPRDs, where it has been shown that blow-out can occur. A solution has been presented which can be used to avoid blow-out. However, it is acknowledged that there is an absence of experimental studies in this direction. It is a recommendation for future work that experimental studies are undertaken in this direction, including of alternative TPRD geometries.

6. Conclusions

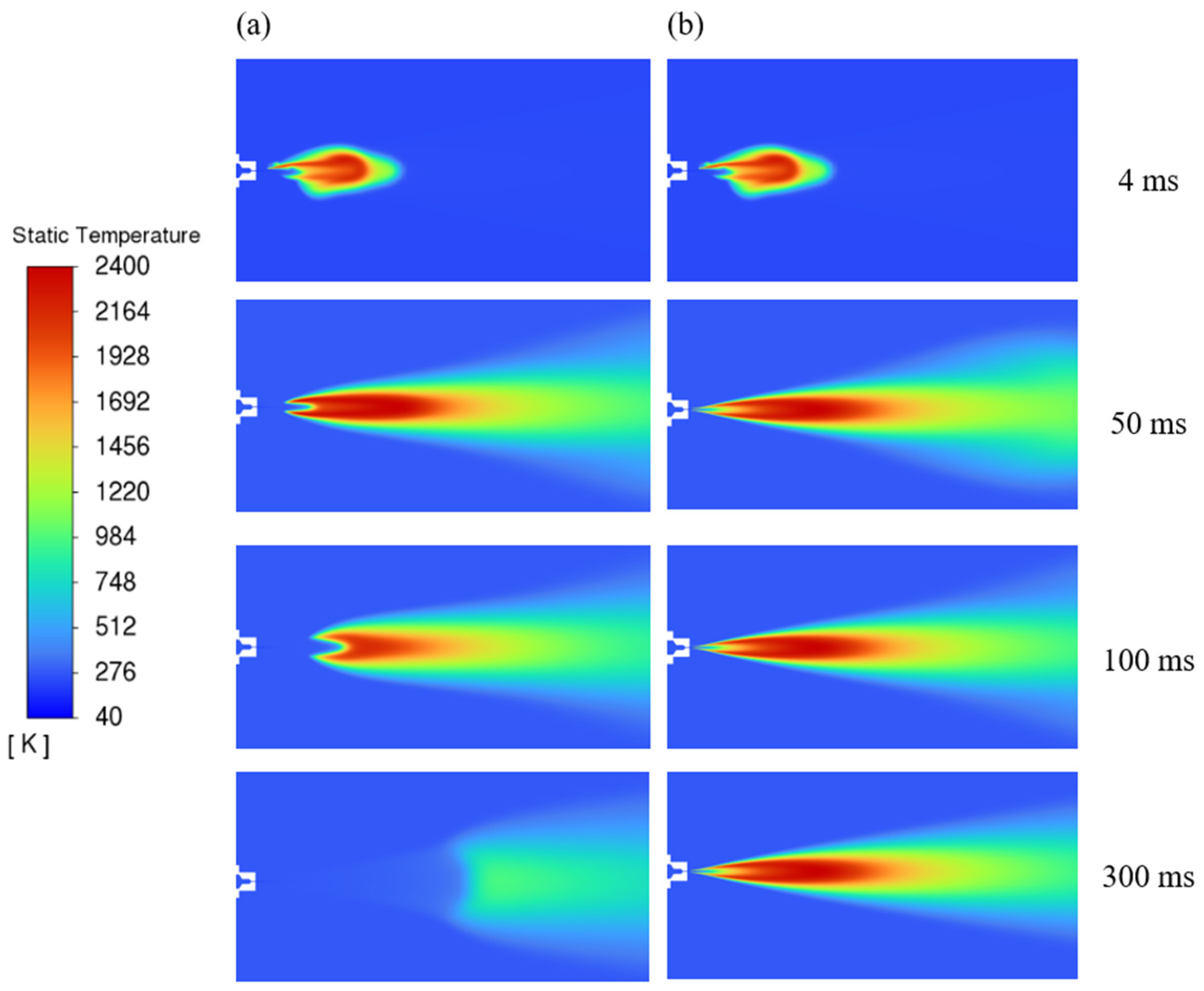
The CFD model has successfully been applied to simulate hydrogen flame stability as driving pressure decreases in a scenario representative of blowdown through a TPRD on a storage tank. This is the first time that dynamic hydrogen flame behaviour during tank blowdown has been demonstrated numerically or experimentally.

This work is original in that it captures the dynamic process of transition from sustained flame to blow-out during reduction in pressure during tank blowdown for a standard TPRD geometry yet demonstrates that a sustained flame is maintained during the entire blowdown process when a nozzle is designed by employing principles of hydrogen safety engineering. Insight is also provided to the relationship between predicted flame edge, waistline position, and flame behaviour.

The rigour of this work is the validation of the CFD model against published work to numerically reproduce the critical diameter for hydrogen, and hydrogen flame behaviour for both standard (single) and “double-diameter” nozzles. There is an absence of experiments demonstrating flame behaviour during tank blow-down, and this is recommended for further studies.

The significance of this work is in the application of the validated model to the real practical scenario of hydrogen blowdown from onboard storage through a TPRD. Blow-out is demonstrated for a standard TPRD, which has implications for releases in a confined space. A clear safety solution has been shown to sustain a flame despite pressure reduction in a hydrogen tank. This has clear implications for tank manufacturers, safety engineers, and ultimately, the public.