Thermodynamics of Reversible Hydrogen Storage: Are Methoxy-Substituted Biphenyls Better through Oxygen Functionality?
Abstract
:1. Introduction
2. Methodology
- -
- Step I: the possible experimental and empirical methods are involved to obtain and validate the (298.15 K) values;
- -
- Step II: the high-level quantum chemical calculations are performed to compute (g, 298.15 K) values and the possible experimental and empirical methods are involved to validate these results;
- -
- Step III: the liquid-phase (liq, 298.15 K) values are derived according to Equation (1) and a thermodynamic analysis of the LOHC system is performed.
3. Experimental
3.1. Materials
3.2. Experimental and Theoretical Methods
4. Results and Discussion
4.1. Step I: Experimental Absolute Vapour Pressures
4.2. Step I: Experimental Standard Molar Enthalpies of Sublimation/Vaporisation from Vapour Pressure Measurements
4.3. Step I: Validation of Vaporisation Enthalpies Using Structure–Property Correlations
4.3.1. Correlation with the Kovats Indices Jx
4.3.2. Correlation Vaporisation Enthalpies of the Parent Structures
4.3.3. Correlation with Normal Boiling Points Tb
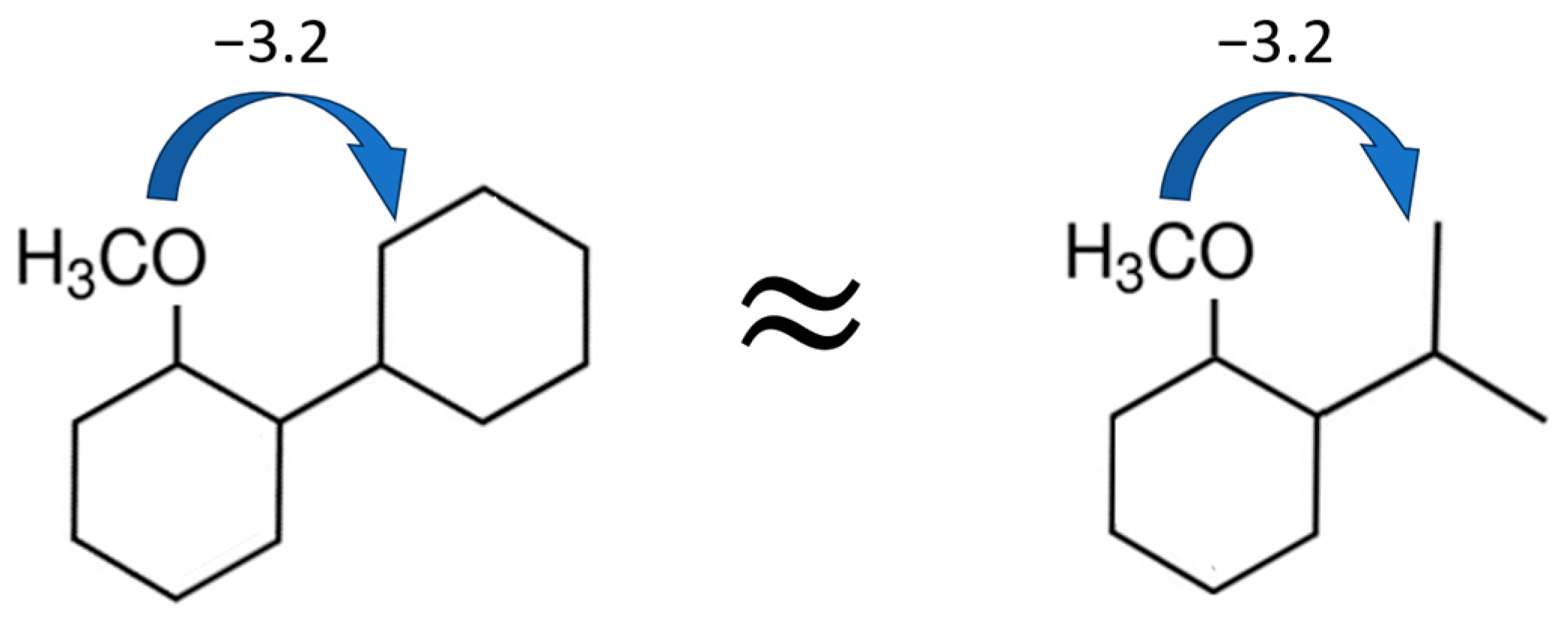
4.4. Step I: Calculation of Vaporisation Enthalpies Using the “Centerpiece” Group-Additivity Concept
4.5. Step II: Gas-Phase Enthalpies of Formation from Quantum Chemical Calculations
4.6. Step III: Energetics of Hydrogenation and Transfer Hydrogenation Reactions Based on Methoxy-Biphenyls
4.7. Thermodynamic Analysis of the Reversible Hydrogenation/Dehydrogenation Process in the Gas Phase
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zaitsau, D.H.; Emel’yanenko, V.N.; Pimerzin, A.A.; Verevkin, S.P. Benchmark properties of biphenyl as a liquid organic hydrogen carrier: Evaluation of thermochemical data with complementary experimental and computational methods. J. Chem. Thermodyn. 2018, 122, 1–12. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, X.; Shi, S.; He, Q.; He, X.; Gan, T.; Ji, H. Highly Efficient Fabrication of Kilogram-Scale Palladium Single-Atom Catalysts for the Suzuki–Miyaura Cross-Coupling Reaction. ACS Appl. Mater. Interfaces 2022, 14, 53755–53760. [Google Scholar] [CrossRef] [PubMed]
- Chen, K.; He, G.; Tang, Q. Air and moisture stable robust bio-polymeric palladium catalyzed C C bond formation and its application to the synthesis of fungicidal. J. Ind. Eng. Chem. 2023, 124, 165–174. [Google Scholar] [CrossRef]
- Sun, Z.; Duan, L.; Huang, C.; Wu, B. Preparation of Biphenyl Derivatives by Using Magnetic Ctalyst in Liquid-Solid Reaction China. CN116143573 A 23 May 2023. [Google Scholar]
- Gelis, C.; Heusler, A.; Nairoukh, Z.; Glorius, F. Catalytic Transfer Hydrogenation of Arenes and Heteroarenes. Chem.-A Eur. J. 2020, 26, 14090–14094. [Google Scholar] [CrossRef]
- Sievi, G.; Geburtig, D.; Skeledzic, T.; Bösmann, A.; Preuster, P.; Brummel, O.; Waidhas, F.; Montero, M.A.; Khanipour, P.; Katsounaros, I.; et al. Towards an efficient liquid organic hydrogen carrier fuel cell concept. Energy Environ. Sci. 2019, 12, 2305–2314. [Google Scholar] [CrossRef]
- Zakgeym, D.; Engl, T.; Mahayni, Y.; Müller, K.; Wolf, M.; Wasserscheid, P. Development of an efficient Pt/SiO2 catalyst for the transfer hydrogenation from perhydro-dibenzyltoluene to acetone. Appl. Catal. A Gen. 2022, 639, 118644. [Google Scholar] [CrossRef]
- Zakgeym, D.; Hofmann, J.D.; Maurer, L.A.; Auer, F.; Müller, K.; Wolf, M.; Wasserscheid, P. Better through oxygen functionality? The benzophenone/dicyclohexylmethanol LOHC-system. Sustain. Energy Fuels 2023, 7, 1213–1222. [Google Scholar] [CrossRef]
- Peterson, K.A.; Feller, D.; Dixon, D.A. Chemical accuracy in ab initio thermochemistry and spectroscopy: Current strategies and future challenges. Theor. Chem. Acc. 2012, 131, 1079. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Curtiss, L.A.; Redfern, P.C.; Raghavachari, K. Gaussian-4 theory. J. Chem. Phys. 2007, 126, 084108. [Google Scholar] [CrossRef]
- Samarov, A.A.; Verevkin, S.P. Comprehensive thermodynamic study of alkyl-biphenyls as a promising Liquid Organic Hydrogen Carriers. J. Chem. Thermodyn. 2022, 174, 106872. [Google Scholar] [CrossRef]
- Kováts, E. Gas-chromatographische Charakterisierung organischer Verbindungen. Teil 1: Retentionsindices aliphatischer Halogenide, Alkohole, Aldehyde und Ketone. Helv. Chim. Acta 1958, 41, 1915–1932. [Google Scholar] [CrossRef]
- Okumura, T. Retention Indices of Environmental Chemicals on Methyl Silicone Capillary Column. J. Environ. Chem. 1991, 1, 333–358. [Google Scholar] [CrossRef]
- Verevkin, S.P.; Konnova, M.E.; Turovtsev, V.V.; Riabchunova, A.V.; Pimerzin, A.A. Weaving a Network of Reliable Thermochemistry around Lignin Building Blocks: Methoxy-Phenols and Methoxy-Benzaldehydes. Ind. Eng. Chem. Res. 2020, 59, 22626–22639. [Google Scholar] [CrossRef]
- Benson, S.W. Thermochemical Kinetics, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 1976; pp. 1–320. [Google Scholar]
- Verevkin, S.P.; Andreeva, I.V.; Zherikova, K.V.; Pimerzin, A.A. Prediction of thermodynamic properties: Centerpiece approach—How do we avoid confusion and get reliable results? J. Therm. Anal. Calorim. 2022, 147, 8525–8534. [Google Scholar] [CrossRef]
- Pracht, P.; Bohle, F.; Grimme, S. Automated exploration of the low-energy chemical space with fast quantum chemical methods. Phys. Chem. Chem. Phys. 2020, 22, 7169–7192. [Google Scholar] [CrossRef]
- Petersson, G.A.; Bennett, A.; Tensfeldt, T.G.; Al-Laham, M.A.; Shirley, W.A.; Mantzaris, J. A complete basis set model chemistry. I. The total energies of closed-shell atoms and hydrides of the first-row elements. J. Chem. Phys. 1988, 89, 2193–2218. [Google Scholar] [CrossRef]
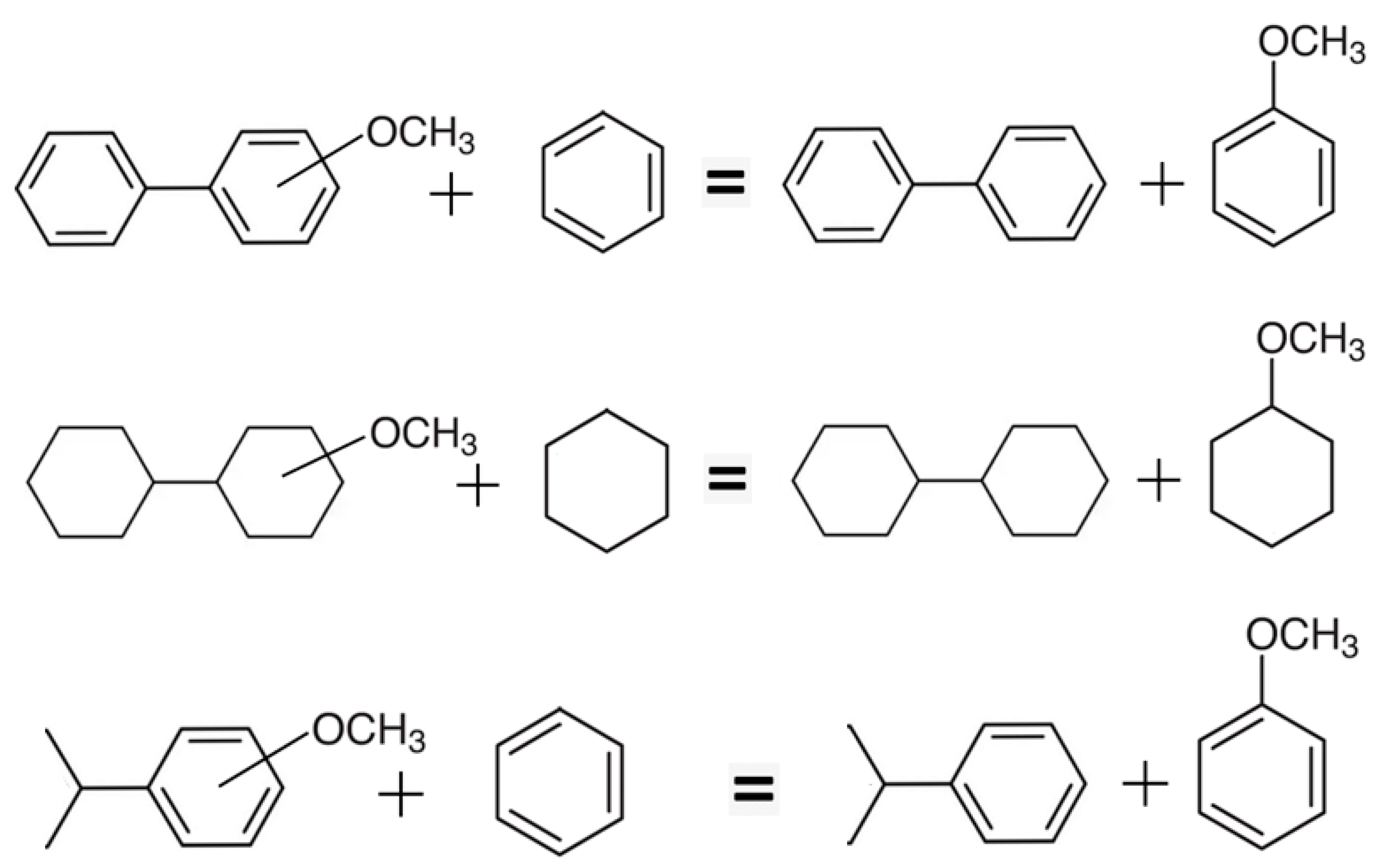
- Wheeler, S.E.; Houk, K.N.; Schleyer, P.v.R.; Allen, W.D. A Hierarchy of Homodesmotic Reactions for Thermochemistry. J. Am. Chem. Soc. 2009, 131, 2547–2560. [Google Scholar] [CrossRef]
- Müller, K.; Stark, K.; Emel’yanenko, V.N.; Varfolomeev, M.A.; Zaitsau, D.H.; Shoifet, E.; Schick, C.; Verevkin, S.P.; Arlt, W. Liquid Organic Hydrogen Carriers: Thermophysical and Thermochemical Studies of Benzyl- and Dibenzyl-toluene Derivatives. Ind. Eng. Chem. Res. 2015, 54, 7967–7976. [Google Scholar] [CrossRef]
- Müller, K.; Völkl, J.; Arlt, W. Thermodynamic Evaluation of Potential Organic Hydrogen Carriers. Energy Technol. 2013, 1, 20–24. [Google Scholar] [CrossRef]
- Verevkin, S.P.; Emel’yanenko, V.N.; Siewert, R.; Pimerzin, A.A. Energetics of LOHC: Structure-Property Relationships from Network of Thermochemical Experiments and in Silico Methods. Hydrogen 2021, 2, 101–121. [Google Scholar] [CrossRef]
- Kulikov, D.; Verevkin, S.P.; Heintz, A. Determination of Vapor Pressures and Vaporization Enthalpies of the Aliphatic Branched C 5 and C 6 Alcohols. J. Chem. Eng. Data 2001, 46, 1593–1600. [Google Scholar] [CrossRef]
- Verevkin, S.P.; Emel’yanenko, V.N. Transpiration method: Vapor pressures and enthalpies of vaporization of some low-boiling esters. Fluid Phase Equilib. 2008, 266, 64–75. [Google Scholar] [CrossRef]
- Verevkin, S.P.; Sazonova, A.Y.; Emel’yanenko, V.N.; Zaitsau, D.H.; Varfolomeev, M.A.; Solomonov, B.N.; Zherikova, K.V. Thermochemistry of Halogen-Substituted Methylbenzenes. J. Chem. Eng. Data 2015, 60, 89–103. [Google Scholar] [CrossRef]
- Emel’yanenko, V.N.; Verevkin, S.P. Benchmark thermodynamic properties of 1,3-propanediol: Comprehensive experimental and theoretical study. J. Chem. Thermodyn. 2015, 85, 111–119. [Google Scholar] [CrossRef]
- Emel’yanenko, V.N.; Zaitsau, D.H.; Shoifet, E.; Meurer, F.; Verevkin, S.P.; Schick, C.; Held, C. Benchmark Thermochemistry for Biologically Relevant Adenine and Cytosine. A Combined Experimental and Theoretical Study. J. Phys. Chem. A 2015, 119, 9680–9691. [Google Scholar] [CrossRef]
- Chickos, J.S.; Hosseini, S.; Hesse, D.G.; Liebman, J.F. Heat capacity corrections to a standard state: A comparison of new and some literature methods for organic liquids and solids. Struct. Chem. 1993, 4, 271–278. [Google Scholar] [CrossRef]
- Chickos, J.S.; Acree, W.E. Enthalpies of Vaporization of Organic and Organometallic Compounds, 1880–2002. J. Phys. Chem. Ref. Data 2003, 32, 519–878. [Google Scholar] [CrossRef]
- Verevkin, S.P. Weaving a web of reliable thermochemistry around lignin building blocks: Phenol, benzaldehyde, and anisole. J. Therm. Anal. Calorim. 2022, 147, 6073–6085. [Google Scholar] [CrossRef]
- SciFinder—Chemical Abstracts Service. Available online: http://scifinder.cas.org/ (accessed on 24 April 2023).
- Reaxys. Available online: https://www.reaxys.com/ (accessed on 24 April 2023).
- Guidechem Chemical Network. Available online: https://www.guidechem.com (accessed on 24 April 2023).
- Majer, V.; Svoboda, V. Enthalpies of Vaporization of Organic Compounds: A Critical Review and Data Compilation; Blackwell Scientific Publications: Oxford, UK, 1985. [Google Scholar]
- Emel’yanenko, V.N.; Zaitseva, K.V.; Agapito, F.; Martinho Simões, J.A.; Verevkin, S.P. Benchmark thermodynamic properties of methylanisoles: Experimental and theoretical study. J. Chem. Thermodyn. 2015, 85, 155–162. [Google Scholar] [CrossRef]
- Dreisbach, R.R.; Martin, R.A. Physical Data on Some Organic Compounds. Ind. Eng. Chem. 1949, 41, 2875–2878. [Google Scholar] [CrossRef]
- Stull, D.R. Vapor Pressure of Pure Substances. Organic and Inorganic Compounds. Ind. Eng. Chem. 1947, 39, 517–540. [Google Scholar] [CrossRef]
- Tsuge, S.; Ohtani, H.; Watanabe, C. Pyrolysis—GC/MS Data Book of Synthetic Polymers; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Efimova, A.A.; Druzhinina, A.I.; Varushchenko, R.M.; Dorofeeva, O.V.; Krasnyh, E.L. Phase Equilibria and Thermodynamic Properties of Some Branched Alkyl Ethers. J. Chem. Eng. Data 2009, 54, 2457–2469. [Google Scholar] [CrossRef]
- NIST Chemistry WebBook. Available online: https://webbook.nist.gov/chemistry/ (accessed on 30 August 2023).
- Verevkin, S.P. Determination of the ortho -, para -, and meta -Interactions in secondary -Alkylphenols from Thermochemical Measurements. Berichte der Bunsengesellschaft für Phys. Chemie 1998, 102, 1467–1473. [Google Scholar] [CrossRef]
- Verevkin, S.P. Thermochemistry of phenols: Experimental standard molar enthalpies of formation of 2-phenylphenol, 4-phenylphenol, 2,6-diphenylphenol, and 2,2′- and 4,4′-dihydroxybiphenyl. J. Chem. Thermodyn. 1998, 30, 389–396. [Google Scholar] [CrossRef]
- Bertholon, G.; Giray, M.; Perrin, R.; Vincent-Falquet-Berny, M.F. No. 532.—Etude physicochimique des phenols. OX.—Ethanlpies de combustion et energies de resonance des alcoyl et aryphenols. Bull. Soc. Chim. Fr. 1971, 3180–3187. [Google Scholar]
- Abdelaziz, A.; Zaitsau, D.H.; Kuratieva, N.V.; Verevkin, S.P.; Schick, C. Melting of nucleobases. Getting the cutting edge of “Walden’s Rule.”. Phys. Chem. Chem. Phys. 2019, 21, 12787–12797. [Google Scholar] [CrossRef]
- Walden, P. Über die Schmelzwärme, spezifische Kohäsion und Molekulargrösse bei der Schmelztemperatur. Z. Für Elektrotechnik Und Elektrochem. 1908, 14, 713–724. [Google Scholar] [CrossRef]
- Chickos, J.S.; Hesse, D.G.; Liebman, J.F. Estimating Enthalpies of Sublimation of Hydrocarbons. In Energetics of Organometallic Species; Springer: Dordrecht, The Netherlands, 1992. [Google Scholar]
- Nagrimanov, R.N.; Ziganshin, M.A.; Solomonov, B.N.; Verevkin, S.P. Thermochemistry of drugs: Experimental and theoretical study of analgesics. Struct. Chem. 2019, 30, 247–261. [Google Scholar] [CrossRef]
- Roux, M.V.; Temprado, M.; Chickos, J.S.; Nagano, Y. Critically evaluated thermochemical properties of polycyclic aromatic hydrocarbons. J. Phys. Chem. Ref. Data 2008, 37, 1855–1996. [Google Scholar] [CrossRef]
- Pedley, J.B.; Naylor, R.D.; Kirby, S.P. Thermochemical Data of Organic Compounds; Chapman and Hall: New York, NY, USA, 1986; pp. 1–792. [Google Scholar]
- Konnova, M.E.; Vostrikov, S.V.; Pimerzin, A.A.; Verevkin, S.P. Thermodynamic analysis of hydrogen storage: Biphenyl as affordable liquid organic hydrogen carrier (LOHC). J. Chem. Thermodyn. 2021, 159, 106455. [Google Scholar] [CrossRef]
- Mokbel, I.; Rauzy, E.; Loiseleur, H.; Berro, C.; Jose, J. Vapor pressures of 12 alkylcyclohexanes, cyclopentane, butylcyclopentane and trans-decahydronaphthalene down to 0.5 Pa. Experimental results, correlation and prediction by an equation of state. Fluid Phase Equilib. 1995, 108, 103–120. [Google Scholar] [CrossRef]
- Hückel, W.; Bross, R.; Fechtig, O.; Feltkamp, H.; Geiger, S.; Hanack, M.; Heinzel, M.; Hubele, A.; Kurz, J.; Maier, M.; et al. Beiträge zur Konstellationsanalyse, III Alkoholyse von Toluolsulfonsäureestern, V. Justus Liebigs Ann. Chem. 1959, 624, 142–255. [Google Scholar] [CrossRef]
- Ducros, M.; Gruson, J.F.; Sannier, H. Estimation des enthalpies de vaporisation des composes organiques liquides. Partie 1. Applications aux alcanes, cycloalcanes, alcenes, hydrocarbures benzeniques, alcools, alcanes thiols, chloro et bromoalcanes, nitriles, esters, acides et aldehydes. Thermochim. Acta 1980, 36, 39–65. [Google Scholar] [CrossRef]
- Ducros, M.; Gruson, J.F.; Sannier, H.; Velasco, I. Estimation des enthalpies de vaporisation des composes organiques liquides. Partie 2. Applications aux ethersoxydes, thioalcanes, cetones et amines. Thermochim. Acta 1981, 44, 131–140. [Google Scholar] [CrossRef]
- Verevkin, S.P.; Beckhaus, H.-D.; Belen’kaja, R.S.; Rakus, K.; Rüchardt, C. Geminal substituent effects Part 9. Standard enthalpies of formation and strain free increments of branched esters and ethers. Thermochim. Acta 1996, 279, 47–64. [Google Scholar] [CrossRef]

| T/ K a | m/ mg b | V(N2) c/ dm3 | Ta/ K d | Flow/ dm3·h−1 | p/ Pa e | u(p)/ Pa | / kJ·mol−1 | / J·K−1·mol−1 |
|---|---|---|---|---|---|---|---|---|
| 2-methoxybiphenyl (liq) (298.15 K) = (57.8 ± 0.5) kJ·mol−1 (298.15 K) = (122.4 ± 1.2) J·K−1·mol−1 (298.15 K) = (21.3 ± 0.1) kJ·mol−1 ; pref = 1 Pa | ||||||||
| 283.3 | 1.78 | 4.549 | 297.2 | 4.71 | 5.34 | 0.16 | 58.7 | 125.6 |
| 286.3 | 1.99 | 3.876 | 297.6 | 4.85 | 7.01 | 0.20 | 58.5 | 125.0 |
| 288.7 | 1.92 | 3.006 | 297.6 | 4.75 | 8.67 | 0.24 | 58.4 | 124.5 |
| 290.4 | 2.02 | 2.749 | 298.1 | 4.71 | 9.99 | 0.27 | 58.3 | 124.1 |
| 292.6 | 2.27 | 2.556 | 298.1 | 4.79 | 12.02 | 0.33 | 58.1 | 123.7 |
| 293.2 | 2.15 | 2.304 | 297.2 | 4.77 | 12.63 | 0.34 | 58.1 | 123.5 |
| 296.4 | 2.81 | 2.317 | 298.1 | 4.79 | 16.40 | 0.44 | 57.9 | 122.9 |
| 297.9 | 2.31 | 1.739 | 295.9 | 4.85 | 17.84 | 0.47 | 57.8 | 122.2 |
| 300.4 | 1.88 | 1.124 | 298.1 | 2.25 | 22.56 | 0.59 | 57.6 | 122.0 |
| 301.9 | 2.58 | 1.386 | 298.1 | 2.25 | 25.17 | 0.65 | 57.5 | 121.7 |
| 302.9 | 5.49 | 2.705 | 295.9 | 4.85 | 27.17 | 0.70 | 57.5 | 121.5 |
| 305.1 | 2.03 | 0.861 | 298.1 | 2.25 | 31.74 | 0.82 | 57.3 | 120.9 |
| 307.9 | 6.97 | 2.423 | 297.7 | 4.85 | 38.71 | 0.99 | 57.1 | 120.2 |
| 309.2 | 3.15 | 0.995 | 298.1 | 2.30 | 42.61 | 1.09 | 57.0 | 120.0 |
| 312.9 | 6.66 | 1.615 | 297.7 | 4.85 | 55.44 | 1.41 | 56.8 | 119.2 |
| 315.1 | 3.59 | 0.765 | 297.2 | 2.30 | 62.89 | 1.60 | 56.7 | 118.5 |
| 317.9 | 13.26 | 2.261 | 297.7 | 4.85 | 78.81 | 2.00 | 56.5 | 118.2 |
| 319.3 | 5.30 | 0.842 | 297.2 | 2.30 | 84.44 | 2.14 | 56.4 | 117.8 |
| 323.3 | 4.77 | 0.574 | 298.2 | 2.30 | 111.9 | 2.82 | 56.1 | 117.1 |
| 4-methoxybiphenyl (liq) (298.15 K) = (79.9 ± 0.9) kJ·mol−1 (298.15 K) = (153.4 ± 2.6) J·K−1·mol−1 (298.15 K) = (34.1 ± 0.1) kJ·mol−1 ; pref = 1 Pa | ||||||||
| 363.8 | 1.82 | 0.799 | 295.0 | 3.69 | 30.36 | 0.78 | 75.5 | 140.3 |
| 366.5 | 1.85 | 0.671 | 295.0 | 1.49 | 36.65 | 0.94 | 75.4 | 139.9 |
| 371.8 | 2.21 | 0.573 | 295.0 | 1.72 | 51.34 | 1.31 | 75.0 | 138.8 |
| 376.3 | 2.51 | 0.487 | 295.0 | 1.72 | 68.51 | 1.74 | 74.7 | 138.0 |
| 381.7 | 2.97 | 0.401 | 295.0 | 1.72 | 98.32 | 2.48 | 74.4 | 137.3 |
| 385.5 | 4.00 | 0.430 | 295.0 | 1.72 | 123.6 | 3.11 | 74.1 | 136.6 |
| 390.7 | 5.71 | 0.459 | 295.0 | 1.72 | 165.5 | 4.16 | 73.8 | 135.6 |
| 395.5 | 7.20 | 0.444 | 295.0 | 1.72 | 215.2 | 5.40 | 73.4 | 134.7 |
| 400.6 | 9.48 | 0.430 | 295.0 | 1.72 | 292.8 | 7.34 | 73.1 | 134.0 |
| 4-methoxybiphenyl (cr) (298.15 K) = (99.8 ± 0.7) kJ·mol−1 (298.15 K) = (208.5 ± 1.6) J·K−1·mol−1 (298.15 K) = (37.7 ± 0.1) kJ·mol−1 ; pref = 1 Pa | ||||||||
| 313.1 | 1.31 | 103.9 | 295.0 | 9.98 | 0.17 | 0.01 | 99.3 | 206.7 |
| 323.3 | 1.00 | 23.28 | 295.0 | 9.98 | 0.57 | 0.02 | 98.9 | 205.7 |
| 328.3 | 1.03 | 13.80 | 295.0 | 9.98 | 0.99 | 0.03 | 98.8 | 205.0 |
| 333.5 | 0.91 | 6.970 | 295.0 | 6.15 | 1.73 | 0.05 | 98.6 | 204.4 |
| 338.3 | 0.87 | 3.998 | 295.0 | 6.15 | 2.89 | 0.08 | 98.4 | 204.0 |
| 343.3 | 2.07 | 5.820 | 295.0 | 9.98 | 4.72 | 0.12 | 98.2 | 203.3 |
| 348.1 | 2.24 | 3.822 | 295.0 | 9.97 | 7.81 | 0.22 | 98.0 | 203.0 |
| 353.8 | 0.91 | 0.922 | 295.0 | 3.69 | 13.10 | 0.35 | 97.8 | 202.2 |
| 356.1 | 11.27 | 8.951 | 295.0 | 9.95 | 16.76 | 0.44 | 97.7 | 202.2 |
| 358.9 | 1.56 | 0.984 | 295.0 | 3.69 | 21.11 | 0.55 | 97.6 | 201.7 |
| 362.4 | 2.83 | 1.291 | 295.0 | 3.69 | 29.14 | 0.75 | 97.5 | 201.4 |
| Compounds/CAS | Method a | T-Range/K | Tav | 298.15 K | Ref |
|---|---|---|---|---|---|
| 3-methoxy-biphenyl (liq) | BP | 358–566 | 67.2 ± 1.9 | 77.1 ± 2.7 | Table S3 |
| 2113-56-6 | Jx | 79.3 ± 1.5 | Table S4 | ||
| 78.8 ± 1.3 b | average | ||||
| 2-methoxy-biphenyl (liq) | T | 283.3–323.3 | 57.5 ± 0.4 | 57.8 ± 0.5 | Table 1 |
| 86-26-0 | Jx | 57.6 ± 1.0 | Table S5 | ||
| 57.8 ± 0.4 b | average | ||||
| 4-methoxy-biphenyl (liq) | T | 363.8–400.6 | 74.4 ± 0.8 | 79.9 ± 0.9 | Table 1 |
| 613-37-6 | BP | 430–573 | 63.3 ± 4.2 | 76.5 ± 5.0 | Table S3 |
| 79.9 ± 0.6 b | average | ||||
| Jx | 79.3 ± 1.5 | Table S4 | |||
| 4-methoxy-biphenyl (cr) | T | 313.1–362.4 | 98.4 ± 0.5 | 99.8 ± 0.7 | Table 1 |
| 613-37-6 | PhT | 99.3 ± 1.4 | Table 3 | ||
| 99.7 ± 0.6 b | average | ||||
| 4,4′-dimethoxy-biphenyl (liq) | BP | 388–611 | 78.1 ± 1.8 | 92.4 ± 3.2 | Table S3 |
| 2132-80-1 | Jx | 91.8 ± 1.5 | Table S4 | ||
| 91.9 ± 1.4 b | average | ||||
| 2-methoxy-iso-propylbenzene (liq) | BP | 307–474 | 45.4 ± 3.6 | 50.9 ± 3.8 | Table S3 |
| 2944-47-0 | Jx | 51.6 ± 1.0 | Table S5 | ||
| 51.6 ± 0.9 b | average | ||||
| 3-methoxy-iso-propylbenzene (liq) | BP | 332–484 | 49.9 ± 2.2 | 56.6 ± 2.6 | Table S3 |
| 6380-20-7 | Jx | 58.3 ± 1.5 | Table S4 | ||
| 57.9 ± 1.3 b | average | ||||
| 4-methoxy-iso-propylbenzene (liq) | BP | 331–488 | 51.0 ± 1.6 | 57.6 ± 2.1 | Table S3 |
| 4132-48-3 | Jx | 58.8 ± 1.5 | Table S4 | ||
| 58.4 ± 1.2 b | average | ||||
| 1-methoxy-2-iso-propyl-cyclohexane 103754-94-5 | Tb | 50.7 ± 0.6 | Table S11 | ||
| methoxy-cyclohexane (liq) | BP | 308–409 | 39.6 ± 1.8 | 42.7 ± 1.9 | Table S3 |
| 931-56-6 | Tb | 42.9 ± 0.6 | Table S11 | ||
| Jx | 42.8 ± 1.0 | Table S6 | |||
| CP | 43.2 ± 1.0 | This work | |||
| 43.0 ± 0.5 b | average | ||||
| 2-methoxy-bicyclohexane (liq) 764717-18-2 | CP | 66.1 ± 1.5 | This work | ||
| 3-methoxy-bicyclohexane (liq) 2447033-60-3 | CP | 69.3 ± 1.5 | This work | ||
| 4-methoxy-bicyclohexane (liq) 160153-88-8 | CP | 69.3 ± 1.5 | This work | ||
| 4,4′-dimethoxy-bicyclohexane (liq) | CP | 79.2 ± 1.5 | This work | ||
| 316363-49-2 |
| Tfus | (Tfus) | (298 K) b | (298 K) | (298 K) | |
|---|---|---|---|---|---|
| Compound | K | kJ·mol−1 | kJ·mol−1 | kJ·mol−1 | kJ·mol−1 |
| 4-methoxy-biphenyl | 363.1 | 22.9 ± 0.2 | 19.4 ± 1.1 | 79.9 ± 0.9 c | 99.3 ± 1.4 d |
| 4,4′-dimethoxy-biphenyl | 450.9 | 35.2 ± 0.3 | 25.9 ± 2.8 | 91.9 ± 1.4 c | 117.8 ± 3.1 d |
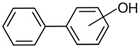 hydroxy-biphenyls | 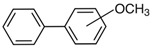 methoxy-biphenyls | ||
|---|---|---|---|
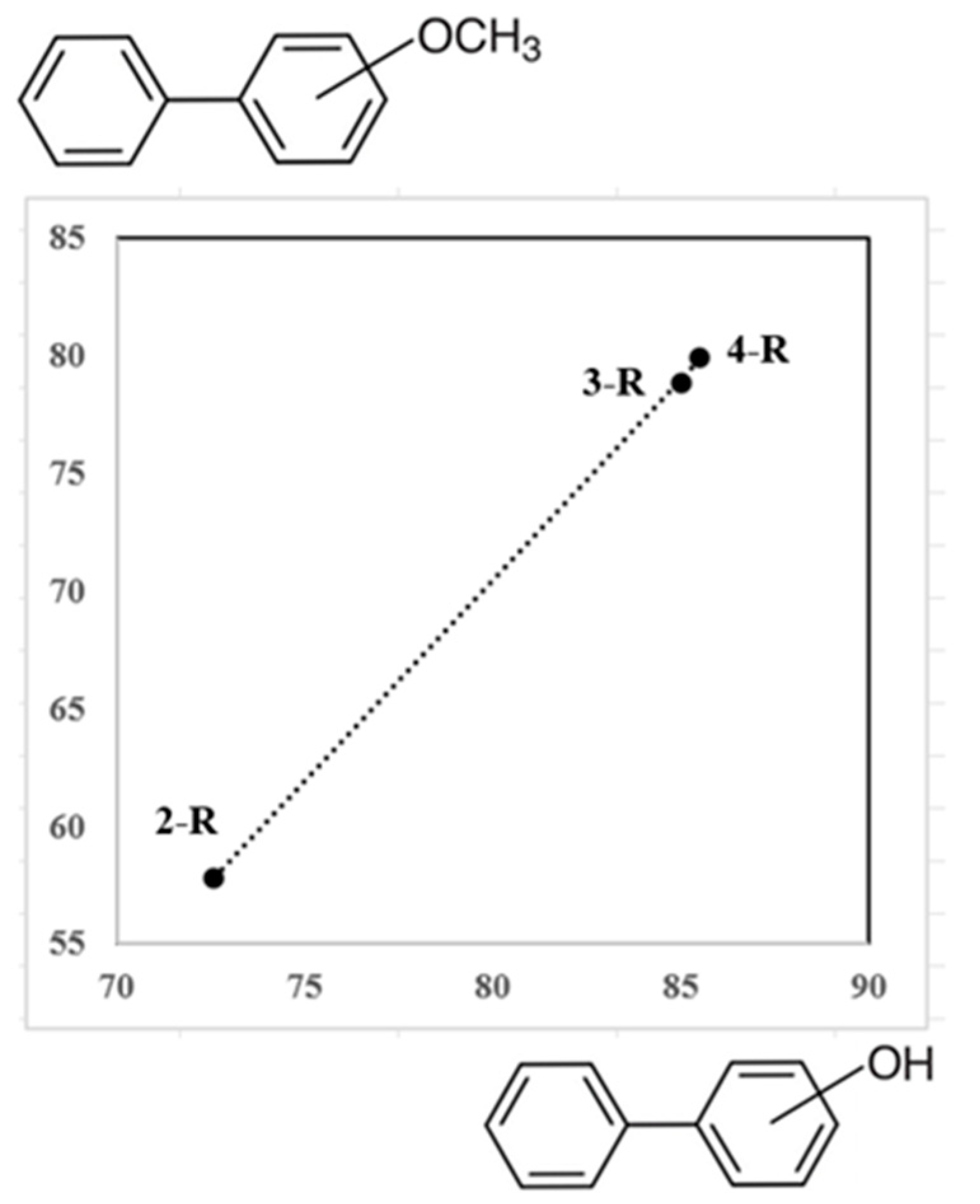
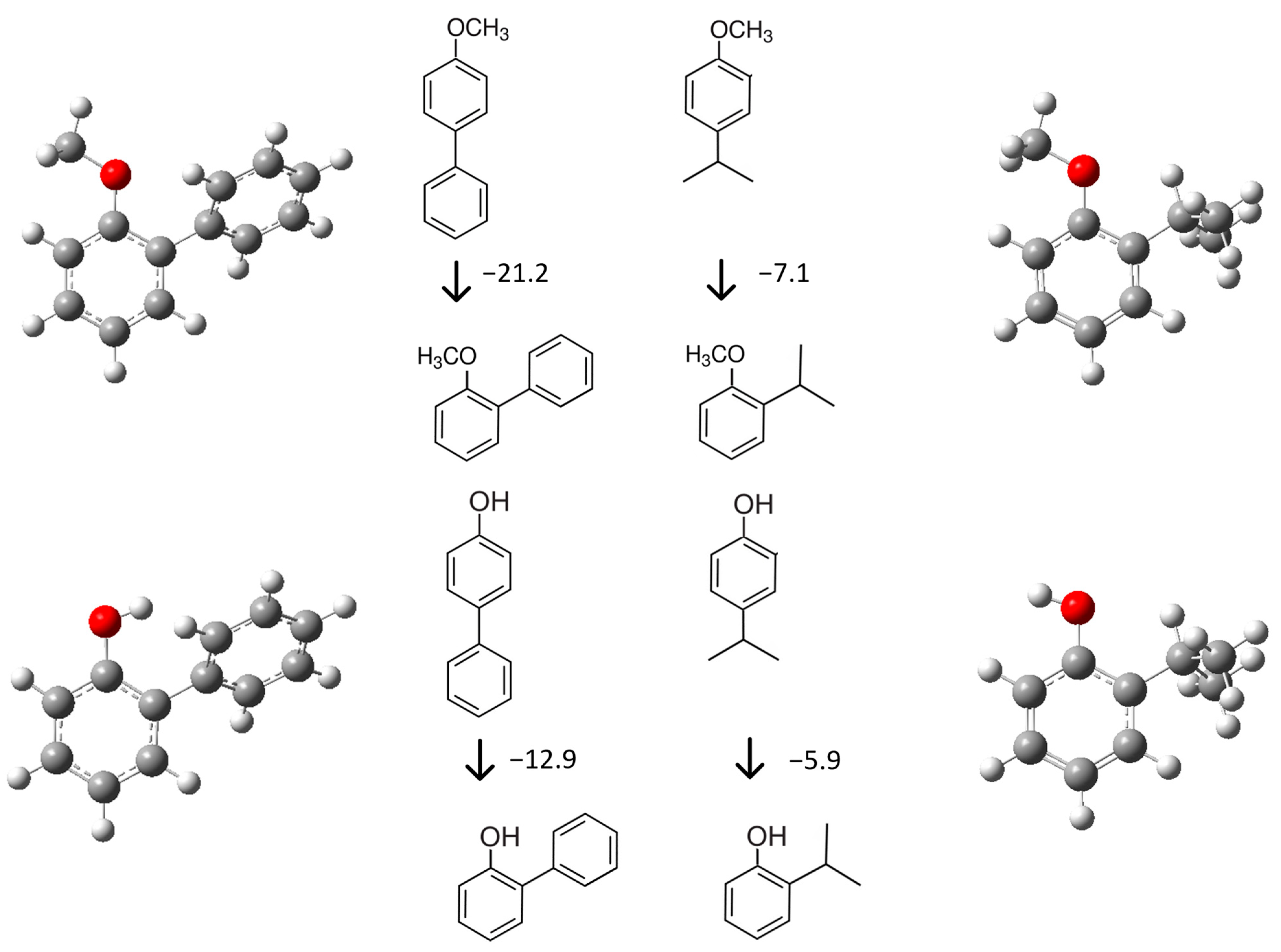
| 2-hydroxy-biphenyl | 72.6 ± 1.4 | 2-methoxy-biphenyl | 57.8 ± 0.4 |
| 3-hydroxy-biphenyl | 85.0 ± 1.0 | 3-methoxy-biphenyl | 78.8 ± 1.3 |
| 4-hydroxy-biphenyl | 85.5 ± 3.0 | 4-methoxy-biphenyl | 79.9 ± 0.9 |
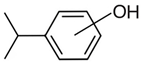 hydroxy-iso-propylbenzenes | (exp) a | 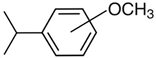 methoxy-iso-propylbenzenes | (exp) b |
|---|---|---|---|
| 2-hydroxy-iso-propylbenzene | 64.4 ± 1.4 | 2-methoxy-iso-propylbenzene | 51.6 ± 0.9 |
| 3-hydroxy-iso-propylbenzene | 70.4 ± 1.0 | 3-methoxy-iso-propylbenzene | 58.3 ± 1.5 |
| 4-hydroxy-iso-propylbenzene | 70.3 ± 1.2 | 4-methoxy-iso-propylbenzene | 58.4 ± 1.2 |
| Compound | (g)AT b | (g)WBR c | (g)CP d | (g)GA e |
|---|---|---|---|---|
| 2-methoxy-biphenyl | 25.3 | 32.0 | - | - |
| 3-methoxy-biphenyl | 19.3 | 26.0 | 26.5 | 26.5 |
| 4-methoxy-biphenyl | 20.2 | 26.9 | 26.5 | 26.5 |
| 4,4’-dimethoxy-biphenyl | −133.9 | −125.6 | −126.7 | −126.7 |
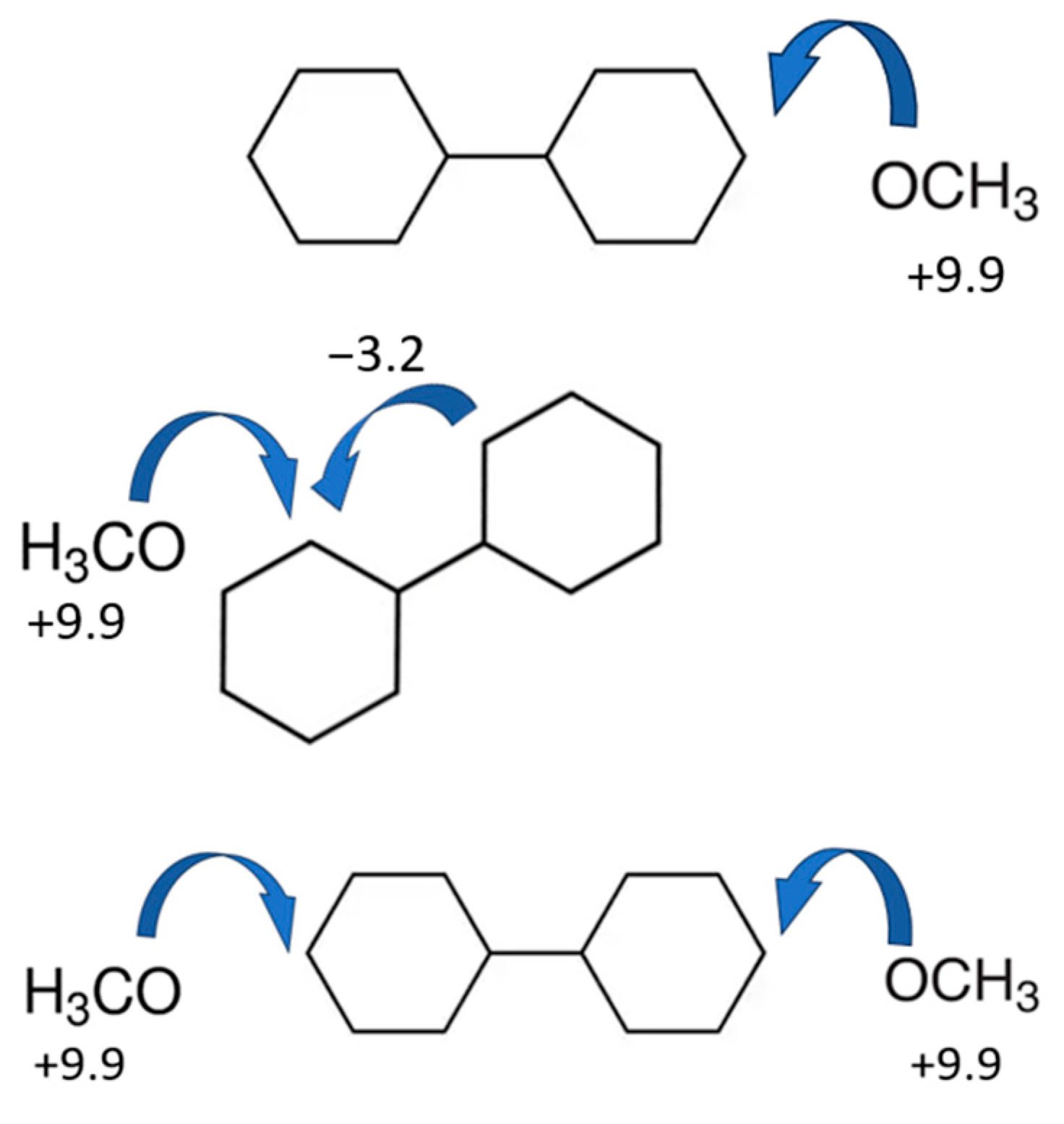
| 2-methoxy-bicyclohexane | −367.5 | −362.1 | - | - |
| 3-methoxy-bicyclohexane | −367.6 | −362.2 | −361.4 | −367.3 |
| 4-methoxy-bicyclohexane | −366.9 | −361.5 | −361.4 | −367.3 |
| 4,4’-dimethoxybicyclohexane | −516.8 | −508.9 | −508.7 | −525.1 |
| 2-methoxy-iso-propylbenzene | −151.3 | −146.1 | - | - |
| 3-methoxy-iso-propylbenzene | −155.1 | −149.9 | −149.2 | −154.2 |
| 4-methoxy-iso-propylbenzene | −153.2 | −148.0 | −149.2 | −154.2 |
| 1-methoxy-2-iso-propyl-cyclohexane | −346.1 | −343.6 | - | - |
| 1-methoxy-3-iso-propyl-cyclohexane | −346.8 | −344.3 | −343.5 | −349.5 |
| 1-methoxy-4-iso-propyl-cyclohexane | −346.0 | −343.5 | −343.5 | −349.5 |
| Compound | (g)WBR b | c | (liq)theor d |
|---|---|---|---|
| 2-methoxy-biphenyl | 32.0 | 57.8 ± 0.4 | −25.8 ± 3.5 |
| 3-methoxy-biphenyl | 26.0 | 78.8 ± 1.3 | −52.8 ± 3.7 |
| 4-methoxy-biphenyl | 26.9 | 79.9 ± 0.9 | −53.0 ± 3.6 |
| 4,4’-dimethoxy-biphenyl | −125.6 | 91.9 ± 1.4 | −217.5 ± 3.7 |
| methoxy-cyclohexane | −270.7 e | 43.0 ± 0.5 | −313.7 ± 3.5 |
| 2-methoxy-bicyclohexane | −362.1 | 66.1 ± 1.5 | −428.2 ± 3.8 |
| 3-methoxy-bicyclohexane | −362.2 | 69.3 ± 1.5 | −431.5 ± 3.8 |
| 4-methoxy-bicyclohexane | −361.5 | 69.3 ± 1.5 | −430.8 ± 3.8 |
| 4,4’-dimethoxy-bicyclohexane | −508.9 | 79.2 ± 1.5 | −588.1 ± 3.8 |
| Compound | (liq)HL a | (liq)HR b | (liq) c | (liq)/H2 d |
|---|---|---|---|---|
| methoxy-benzene | −116.9 ± 0.7 e | −313.7 ± 3.5 e | −196.8 | −65.6 |
| 2-methoxy-biphenyl | −25.8 ± 3.5 | −428.2 ± 3.8 | −402.4 | −67.1 |
| 3-methoxy-biphenyl | −52.8 ± 3.7 | −431.5 ± 3.8 | −378.7 | −63.1 |
| 4-methoxy-biphenyl | −53.0 ± 3.6 | −430.8 ± 3.8 | −377.8 | −63.0 |
| 4,4’-dimethoxy-biphenyl | −217.5 ± 3.7 | −588.1 ± 3.8 | −370.6 | −61.7 |
| Compound | (liq)AC a | (liq)iPr b | (liq)HR c | (liq)HL d | (liq) e |
|---|---|---|---|---|---|
| methoxy-cyclohexane | −248.1 ± 0.7 | −318.1 ± 0.5 | −313.7 ± 3.5 | −116.9 ± 0.7 | −13.2 |
| 2-methoxy-bicyclohexane | −248.1 ± 0.7 | −318.1 ± 0.5 | −428.2 ± 3.8 | −25.8 ± 3.5 | −17.6 |
| 3-methoxy-bicyclohexane | −248.1 ± 0.7 | −318.1 ± 0.5 | −431.5 ± 3.8 | −52.8 ± 3.7 | −41.3 |
| 4-methoxy-bicyclohexane | −248.1 ± 0.7 | −318.1 ± 0.5 | −430.8 ± 3.8 | −53.0 ± 3.6 | −42.2 |
| 4,4’-dimethoxy-bicyclohexane | −248.1 ± 0.7 | −318.1 ± 0.5 | −588.1 ± 3.8 | −217.5 ± 3.7 | −49.4 |
| HR-Counterpart | Teq | |||
|---|---|---|---|---|
| methoxy-cyclohexane | −87.3 | −195.2 | −362.0 | 539 |
| bicyclohexane | −162.2 | −383.2 | −741.1 | 517 |
| 2-methoxy-bicyclohexane | −166.7 | −384.4 | −729.9 | 527 |
| 3-methoxy-bicyclohexane | −160.4 | −378.5 | −731.4 | 518 |
| 4-methoxy-bicyclohexane | −160.6 | −378.6 | −731.3 | 518 |
| 4,4’-dimethoxy-bicyclohexane | −158.3 | −374.5 | −725.2 | 516 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Verevkin, S.P.; Samarov, A.A.; Vostrikov, S.V. Thermodynamics of Reversible Hydrogen Storage: Are Methoxy-Substituted Biphenyls Better through Oxygen Functionality? Hydrogen 2023, 4, 862-880. https://doi.org/10.3390/hydrogen4040052
Verevkin SP, Samarov AA, Vostrikov SV. Thermodynamics of Reversible Hydrogen Storage: Are Methoxy-Substituted Biphenyls Better through Oxygen Functionality? Hydrogen. 2023; 4(4):862-880. https://doi.org/10.3390/hydrogen4040052
Chicago/Turabian StyleVerevkin, Sergey P., Artemiy A. Samarov, and Sergey V. Vostrikov. 2023. "Thermodynamics of Reversible Hydrogen Storage: Are Methoxy-Substituted Biphenyls Better through Oxygen Functionality?" Hydrogen 4, no. 4: 862-880. https://doi.org/10.3390/hydrogen4040052
APA StyleVerevkin, S. P., Samarov, A. A., & Vostrikov, S. V. (2023). Thermodynamics of Reversible Hydrogen Storage: Are Methoxy-Substituted Biphenyls Better through Oxygen Functionality? Hydrogen, 4(4), 862-880. https://doi.org/10.3390/hydrogen4040052







