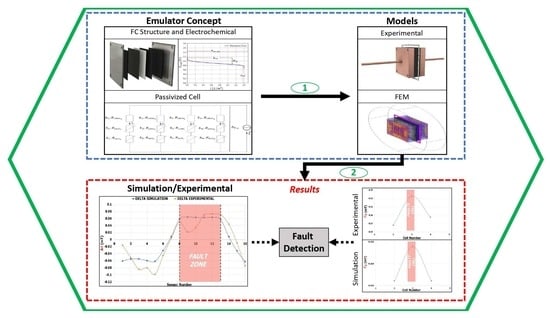
An Innovative PEMFC Magnetic Field Emulator to Validate the Ability of a Magnetic Field Analyzer to Detect 3D Faults
Abstract
1. Introduction
2. 3D PEMFC Current Density Emulator
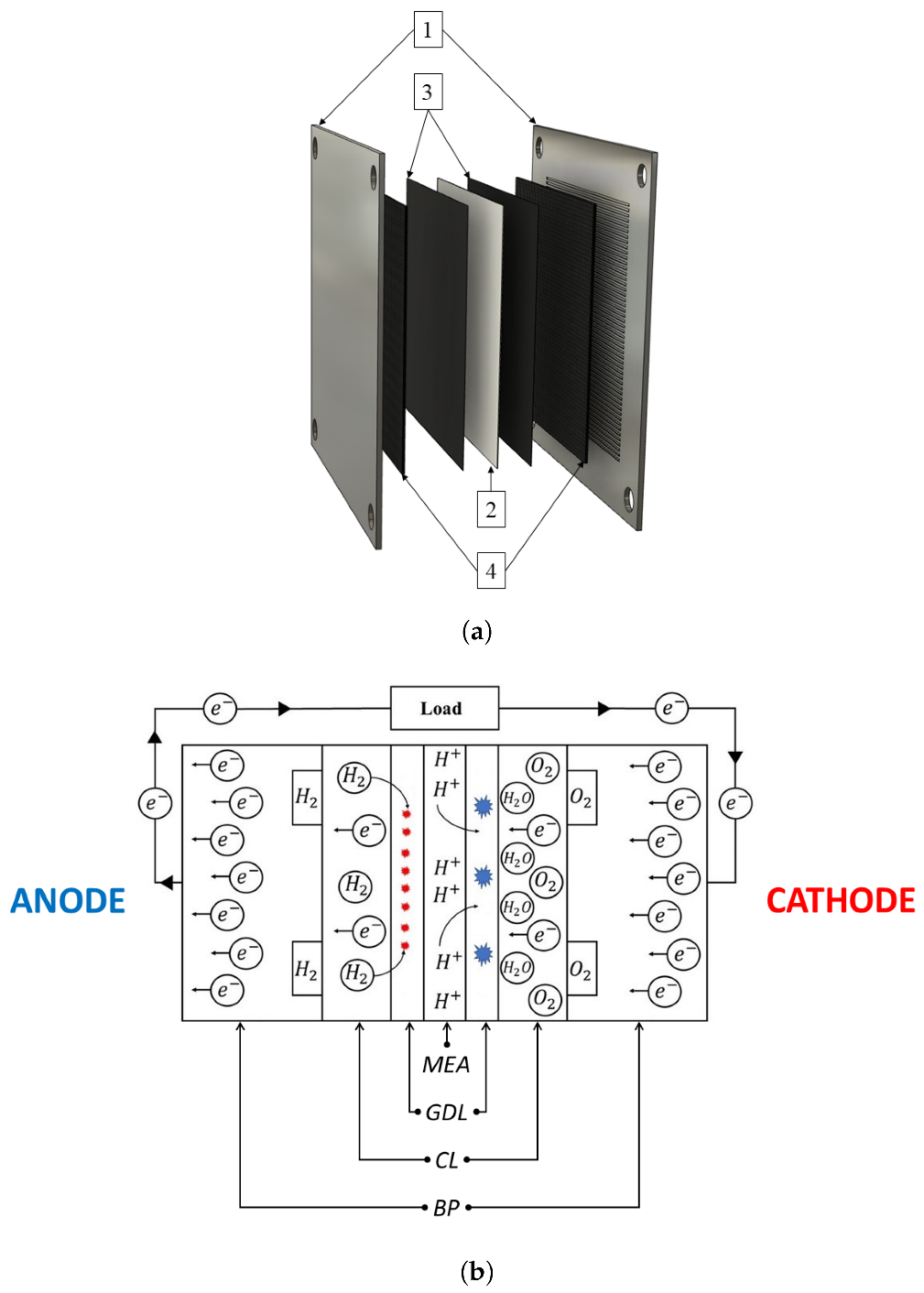
2.1. FC Structure and Electrochemical Consideration
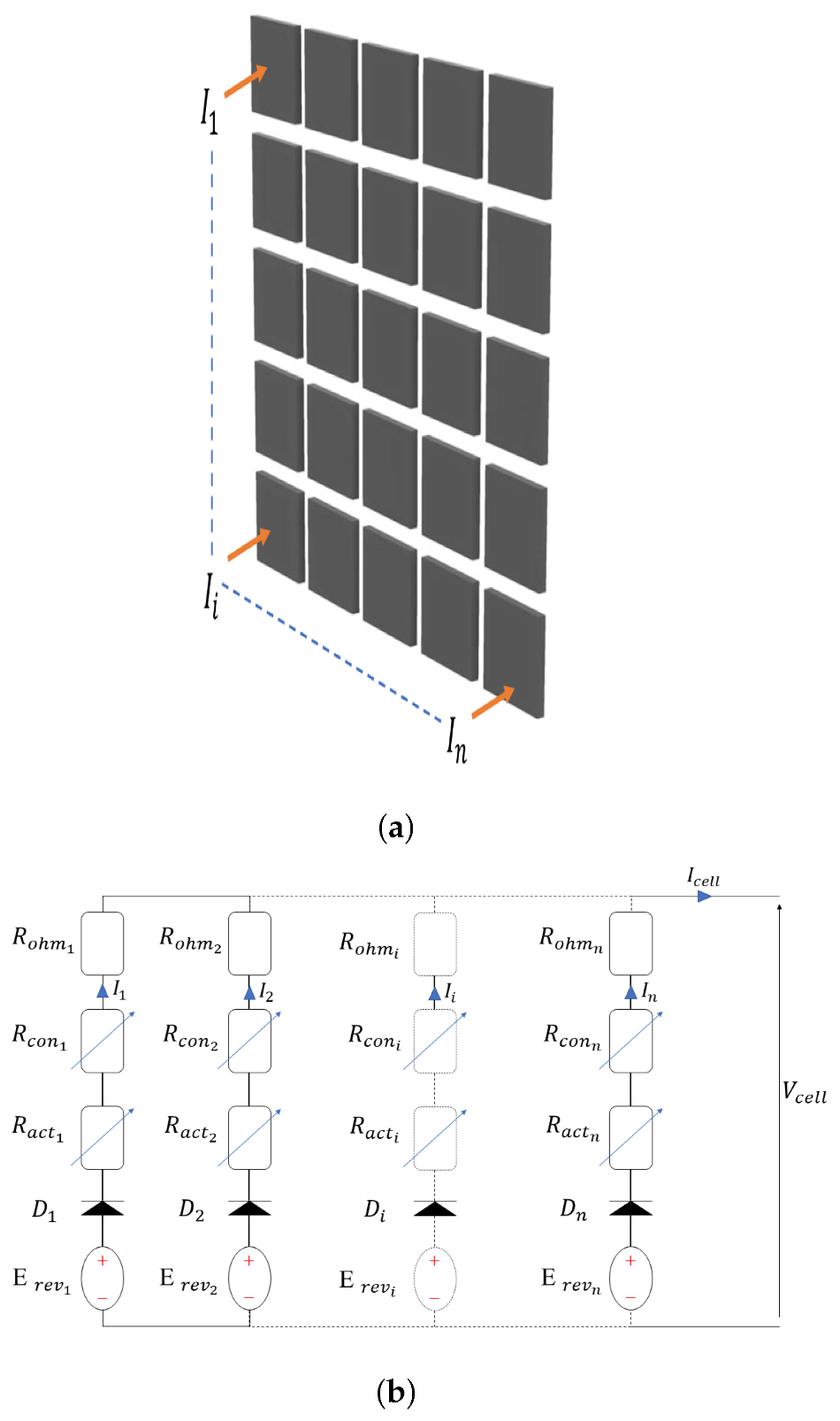
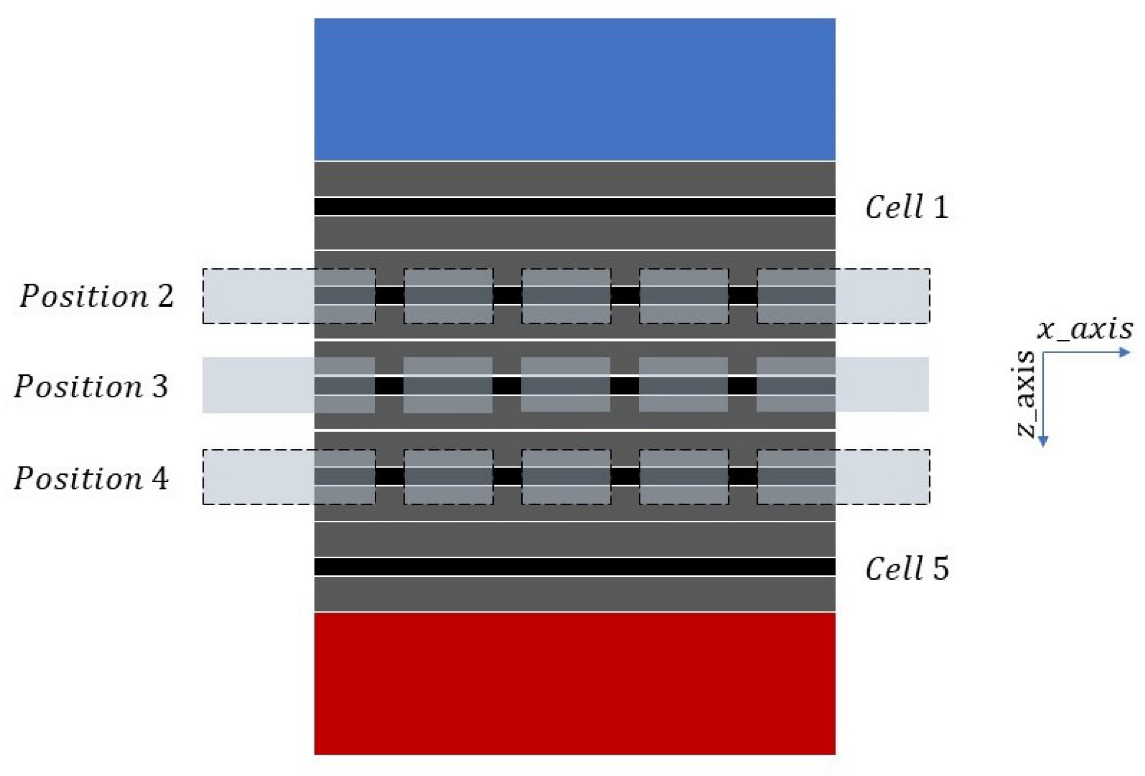
2.2. Current Density Distribution inside the Real FC and the Proposed Emulator
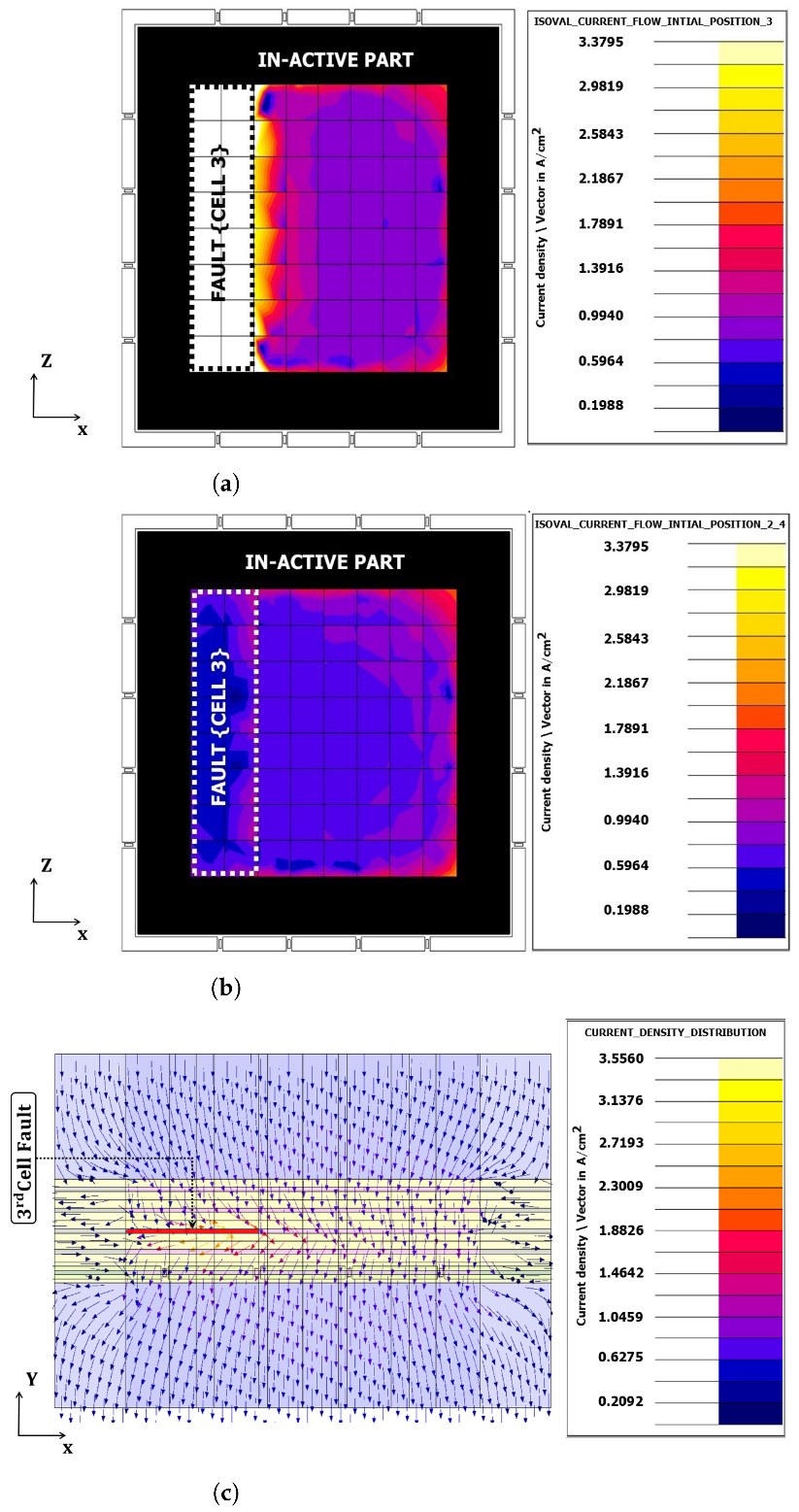
2.2.1. Current Density Distribution inside the FC
2.2.2. A FC Emulator Concept
- If then which can be equivalent with a very high resistivity of
- If then
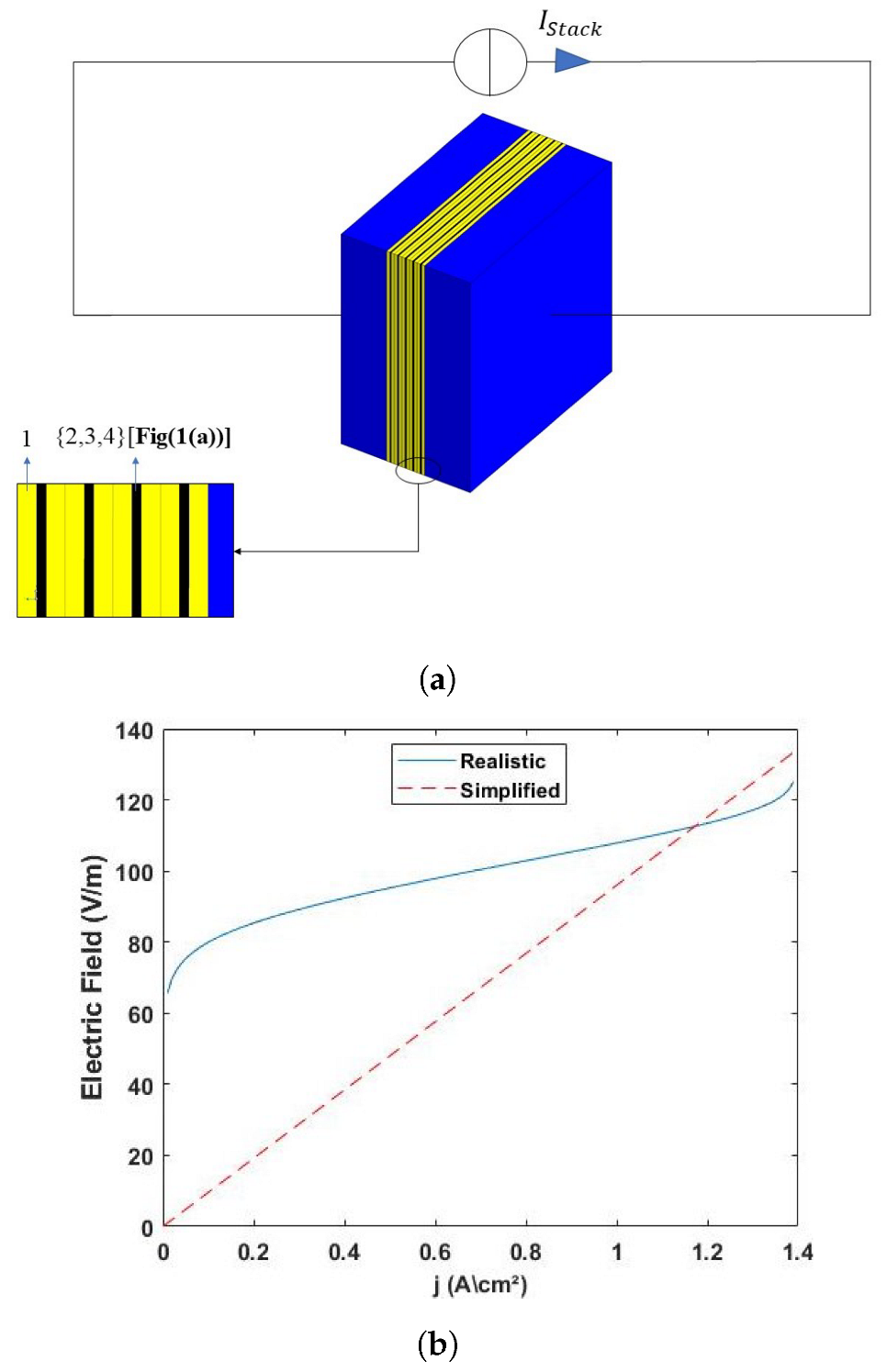
2.2.3. Electric Conduction Problem of the Passivized FC
3. Experimental and Numerical Modeling Results
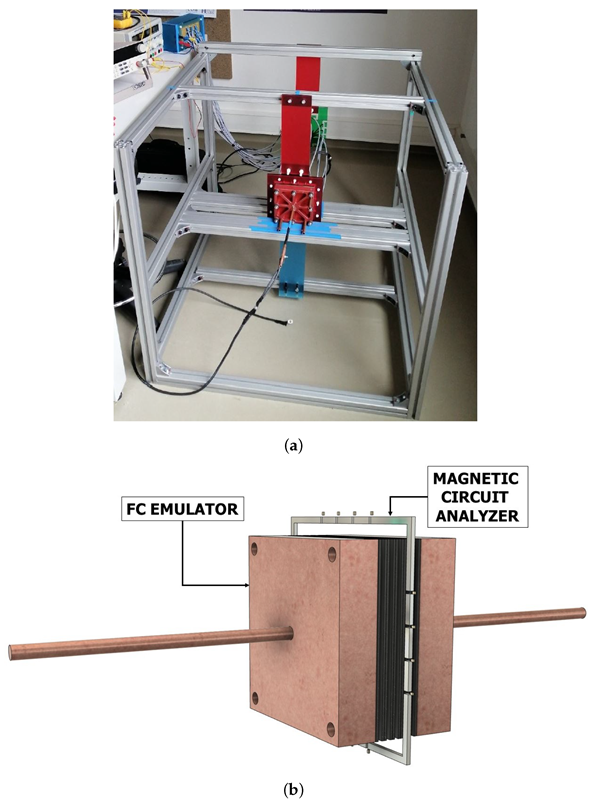
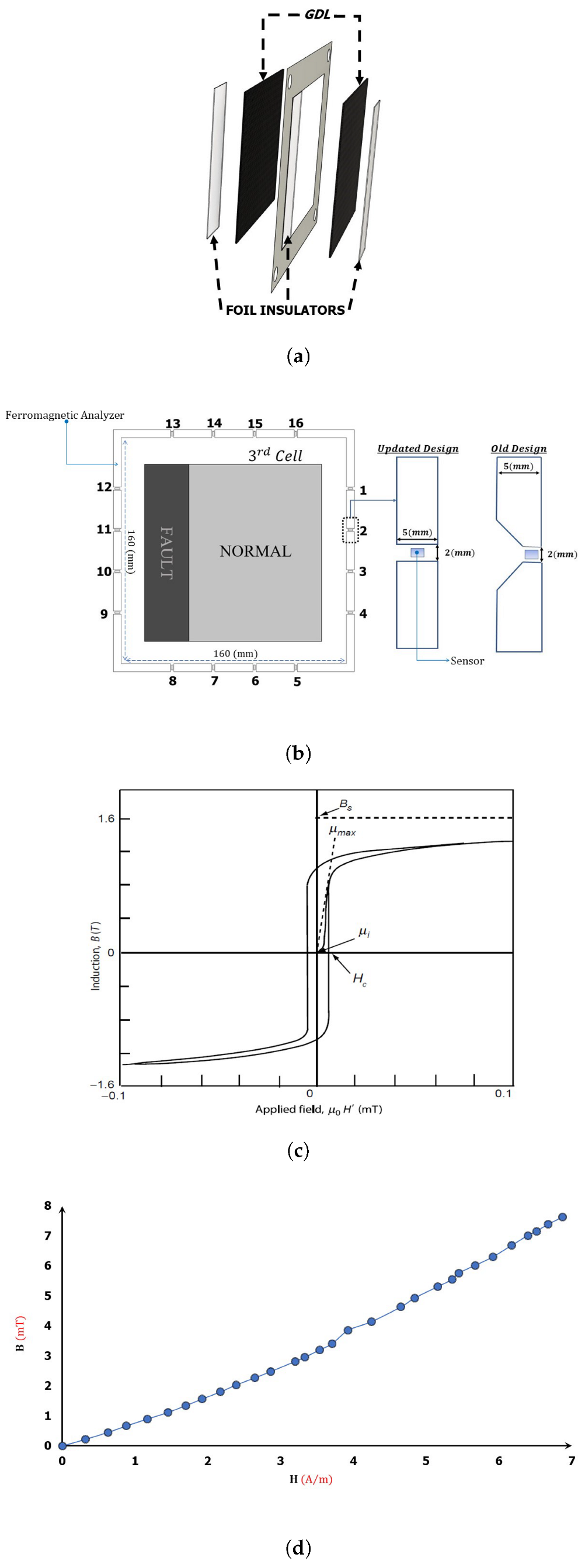
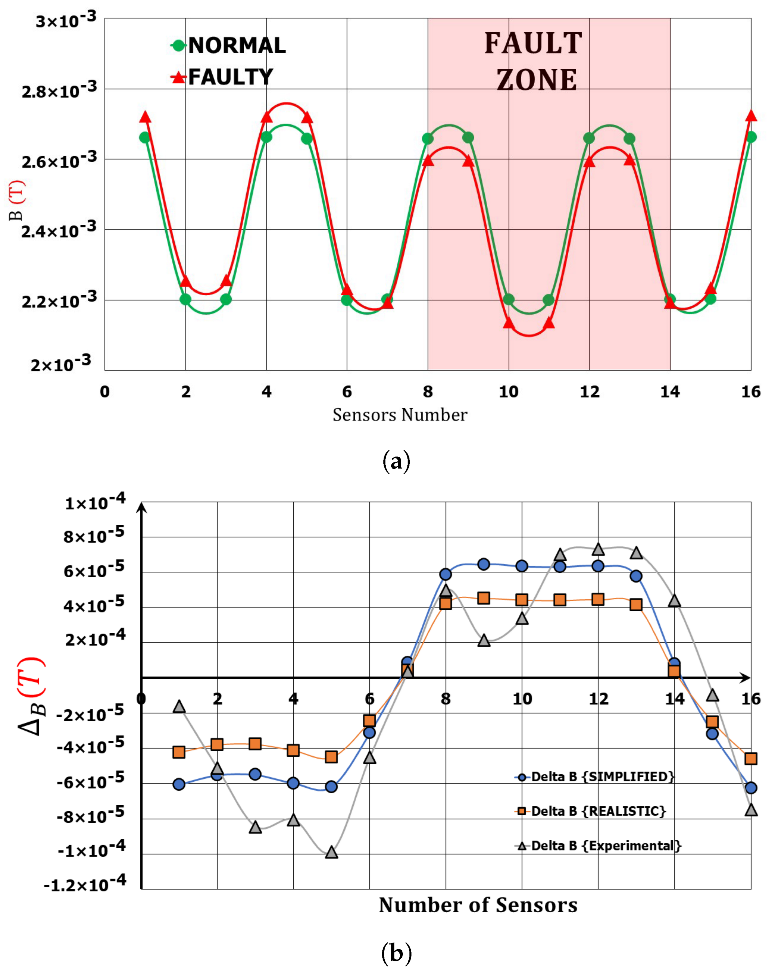
3.1. Experimental Setup and Results
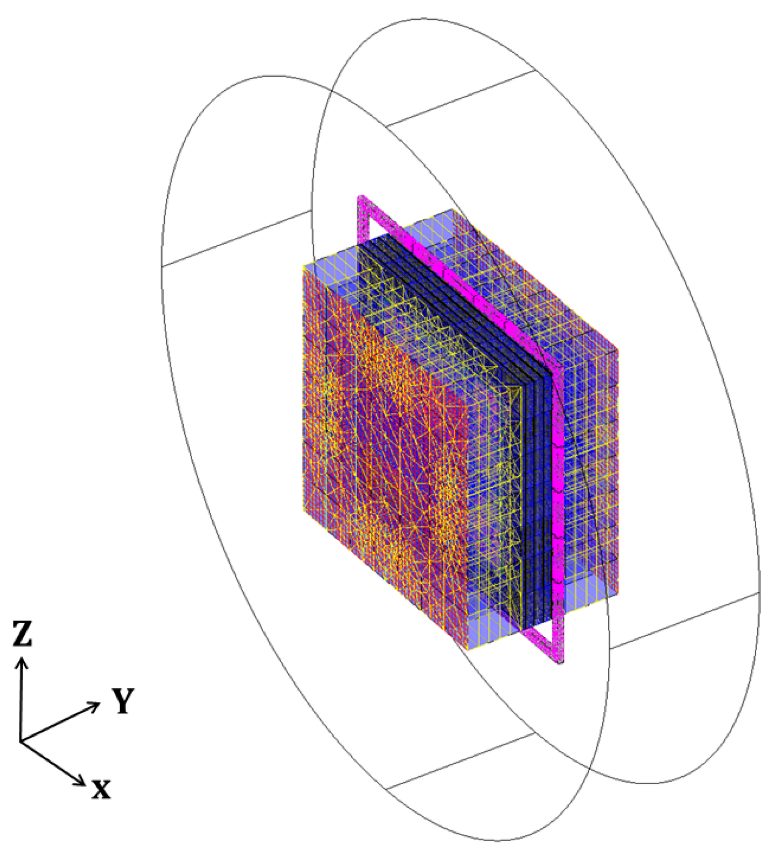
3.2. Numerical Modeling and Results
3.2.1. Coupled Electric Conduction and Magnetic Formulations
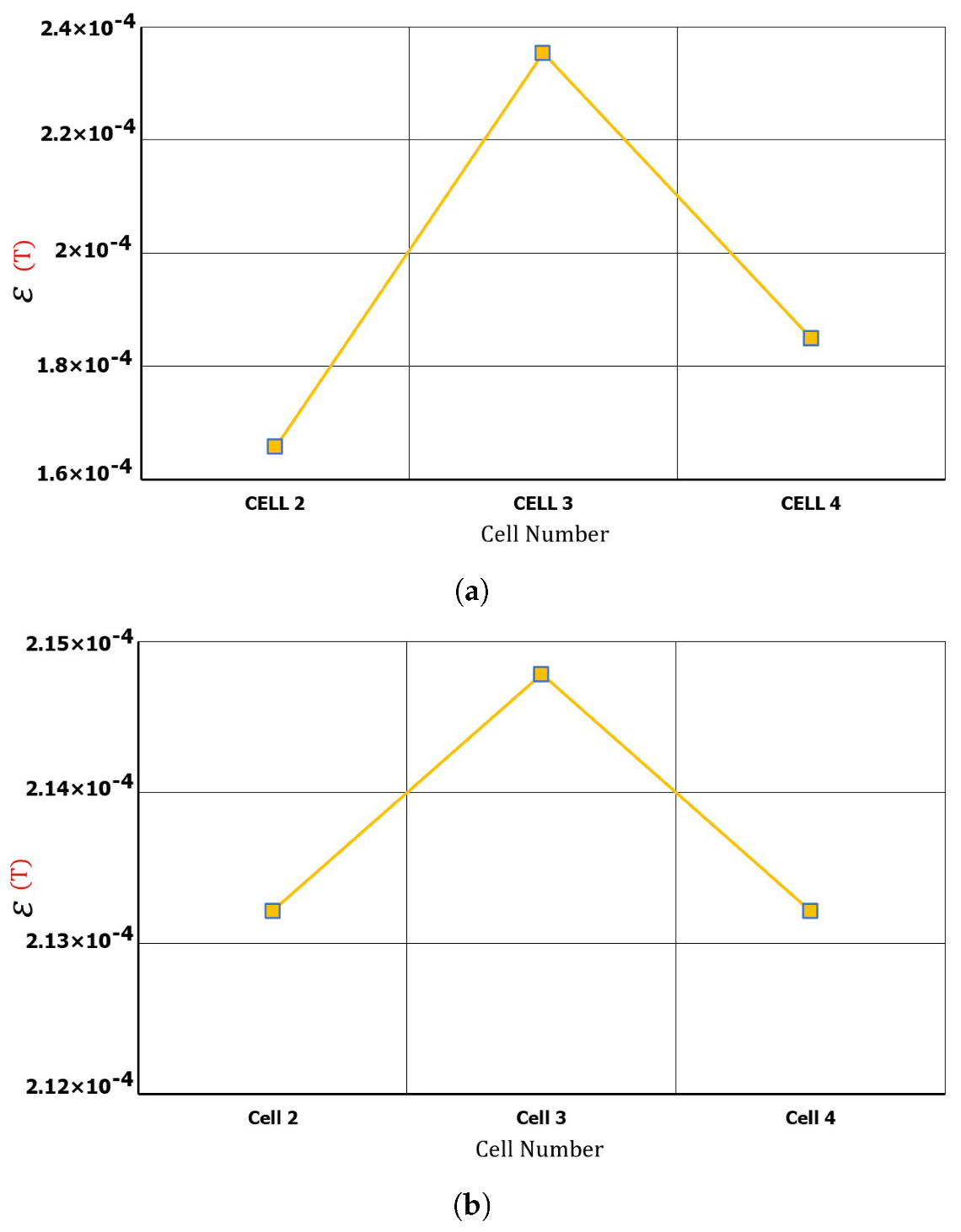
3.2.2. Fault Cell Detection Using Magnetic Field Measurements
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Perry, M.; Fuller, T. A historical perspective of fuel cell technology in the 20th century. J. Electrochem. Soc. 2002, 149, S59. [Google Scholar] [CrossRef]
- Mock, P.; Schmid, S. Fuel cells for automotive powertrains—A techno-economic assessment. J. Power Sources 2009, 190, 133–140. [Google Scholar] [CrossRef]
- Minelli, S.; Civelli, M.; Rondinini, S.; Minguzzi, A.; Vertova, A. Aemfc exploiting a pd/ceo2-based anode compared to classic pemfc via lca analysis. Hydrogen 2021, 2, 246–261. [Google Scholar] [CrossRef]
- Handwerker, M.; Wellnitz, J.; Marzbani, H. Comparison of hydrogen powertrains with the battery powered electric vehicle and investigation of small-scale local hydrogen production using renewable energy. Hydrogen 2021, 2, 76–100. [Google Scholar] [CrossRef]
- Lambert, H.; Roche, R.; Jeme, S.; Ortega, P.; Hissel, D. Combined cooling and power management strategy for a standalone house using hydrogen and solar energy. Hydrogen 2021, 2, 207–224. [Google Scholar] [CrossRef]
- Gurz, M.; Baltacioglu, E.; Hames, Y.; Kaya, K. The meeting of hydrogen and automotive: A review. Int. J. Hydrog. Energy 2017, 42, 23334–23346. [Google Scholar] [CrossRef]
- Wilberforce, T.; Alaswad, A.; Palumbo, A.; Dassisti, M.; Olabi, A.-G. Advances in stationary and portable fuel cell applications. Int. J. Hydrog. Energy 2016, 41, 16509–16522. [Google Scholar] [CrossRef]
- Andrews, J.; Shabani, B. Re-envisioning the role of hydrogen in a sustainable energy economy. Int. J. Hydrog. Energy 2012, 37, 1184–1203. [Google Scholar] [CrossRef]
- Knights, S.; Colbow, K.; St-Pierre, J.; Wilkinson, D. Aging mechanisms and lifetime of pefc and dmfc. J. Power Sources 2004, 127, 127–134. [Google Scholar] [CrossRef]
- Taniguchi, A.; Akita, T.; Yasuda, K.; Miyazaki, Y. Analysis of electrocatalyst degradation in pemfc caused by cell reversal during fuel starvation. J. Power Sources 2004, 130, 42–49. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, L.; Mao, Z.; Zhuge, W.; Zhang, Y.; Wang, L. Behavior of pemfc in starvation. J. Power Sources 2006, 157, 166–176. [Google Scholar] [CrossRef]
- Tang, H.; Peikang, S.; Wang, F.; Pan, M. A degradation study of nafion proton exchange membrane of pem fuel cells. J. Power Sources 2007, 170, 85–92. [Google Scholar] [CrossRef]
- Husar, A.; Serra, M.; Kunusch, C. Description of gasket failure in a 7 cell pemfc stack. J. Power Sources 2007, 169, 85–91. [Google Scholar] [CrossRef]
- Yue, M.; Jemei, S.; Gouriveau, R.; Zerhouni, N. Review on health-conscious energy management strategies for fuel cell hybrid electric vehicles: Degradation models and strategies. Int. J. Hydrog. Energy 2019, 44, 6844–6861. [Google Scholar] [CrossRef]
- Wang, J.; Yang, B.; Zeng, C.; Chen, Y.; Guo, Z.; Li, D.; Shao, R.; Shu, H.; Yu, T. Recent advances and summarization of fault diagnosis techniques for proton exchange membrane fuel cell systems: A critical overview. J. Power Sources 2021, 500, 229932. [Google Scholar] [CrossRef]
- Tian, G.; Wasterlain, S.; Endichi, I.; Candusso, D.; Harel, F.; François, X.; Péra, M.-C.; Hissel, D.; Kauffmann, J.-M. Diagnosis methods dedicated to the localisation of failed cells within pemfc stacks. J. Power Sources 2008, 182, 449–461. [Google Scholar] [CrossRef]
- Veziroglu, A.; Macario, R. Fuel cell vehicles: State of the art with economic and environmental concerns. Int. J. Hydrog. Energy 2011, 36, 25–43. [Google Scholar] [CrossRef]
- Rubio, M.A.; Urquia, A.; Dormido, S. Diagnosis of performance degradation phenomena in pem fuel cells. Int. J. Hydrog. Energy 2010, 35, 2586–2590. [Google Scholar] [CrossRef]
- Chevalier, S.; Trichet, D.; Auvity, B.; Olivier, J.C.; Josset, C.; Machmoum, M. Multiphysics dc and ac models of a pemfc for the detection of degraded cell parameters. Int. J. Hydrog. Energy 2013, 38, 11609–11618. [Google Scholar] [CrossRef]
- Petrone, R.; Zheng, Z.; Hissel, D.; Péra, M.-C.; Pianese, C.; Sorrentino, M.; Béchérif, M.; Yousfi-Steiner, N. A review on model-based diagnosis methodologies for pemfcs. Int. J. Hydrog. Energy 2013, 38, 7077–7091. [Google Scholar] [CrossRef]
- Escobet, T.; Feroldi, D.; De Lira, S.; Puig, V.; Quevedo, J.; Riera, J.; Serra, M. Model-based fault diagnosis in pem fuel cell systems. J. Power Sources 2009, 192, 216–223. [Google Scholar] [CrossRef]
- Hissel, D.; Péra, M.C.; Kauffmann, J.M. Diagnosis of automotive fuel cell power generators. J. Power Sources 2004, 128, 239–246. [Google Scholar] [CrossRef]
- Hua, J.; Li, J.; Ouyang, M.; Lu, L.; Xu, L. Proton exchange membrane fuel cell system diagnosis based on the multivariate statistical method. Int. J. Hydrog. Energy 2011, 36, 9896–9905. [Google Scholar] [CrossRef]
- Yousfi Steiner, N.; Hissel, D.; Moçotéguy, P.; Candusso, D. Diagnosis of polymer electrolyte fuel cells failure modes (flooding & drying out) by neural networks modeling. Int. J. Hydrog. Energy 2011, 36, 3067–3075. [Google Scholar]
- Zheng, Z.; Petrone, R.; Péra, M.-C.; Hissel, D.; Béchérif, M.; Pianese, C.; Yousfi Steiner, N.; Sorrentino, M. A review on non-model based diagnosis methodologies for pem fuel cell stacks and systems. Int. J. Hydrog. Energy 2013, 38, 8914–8926. [Google Scholar] [CrossRef]
- Giurgea, S.; Tirnovan, R.; Hissel, D.; Outbib, R. An analysis of fluidic voltage statistical correlation for a diagnosis of pem fuel cell flooding. Int. J. Hydrog. Energy 2013, 38, 4689–4696. [Google Scholar] [CrossRef]
- Chen, H.; Zhao, X.; Qu, B.; Zhang, T.; Pei, P.; Li, C. An evaluation method of gas distribution quality in dynamic process of proton exchange membrane fuel cell. Appl. Energy 2018, 232, 26–35. [Google Scholar] [CrossRef]
- Yuan, X.-Z.R.; Song, C.; Wang, H.; Zhang, J. Electrochemical Impedance Spectroscopy in PEM Fuel Cells: Fundamentals and Applications; Springer Science & Business Media: New York, NY, USA, 2009. [Google Scholar]
- Brunetto, C.; Moschetto, A.; Tina, G. Pem fuel cell testing by electrochemical impedance spectroscopy. Electr. Power Syst. Res. 2009, 79, 17–26. [Google Scholar] [CrossRef]
- Huang, Q.-A.; Hui, R.; Wang, B.; Zhang, J. A review of ac impedance modeling and validation in sofc diagnosis. Electrochim. Acta 2007, 52, 8144–8164. [Google Scholar] [CrossRef]
- Niya, S.M.R.; Hoorfar, M. Study of proton exchange membrane fuel cells using electrochemical impedance spectroscopy technique—A review. J. Power Sources 2013, 240, 281–293. [Google Scholar] [CrossRef]
- Sui, P.-C.; Zhu, X.; Djilali, N. Modeling of pem fuel cell catalyst layers: Status and outlook. Electrochem. Energy Rev. 2019, 2, 428–466. [Google Scholar] [CrossRef]
- Wang, R.; Wang, H.; Luo, F.; Liao, S. Core–shell-structured low-platinum electrocatalysts for fuel cell applications. Electrochem. Energy Rev. 2018, 1, 324–387. [Google Scholar] [CrossRef]
- Depernet, D.; Narjiss, A.; Gustin, F.; Hissel, D.; Péra, M.-C. Integration of electrochemical impedance spectroscopy functionality in proton exchange membrane fuel cell power converter. Int. J. Hydrog. Energy 2016, 41, 5378–5388. [Google Scholar] [CrossRef]
- Robin, C.; Gerard, M.; d’Arbigny, J.; Schott, P.; Jabbour, L.; Bultel, Y. Development and experimental validation of a pem fuel cell 2d-model to study heterogeneities effects along large-area cell surface. Int. J. Hydrog. Energy 2015, 40, 10211–10230. [Google Scholar] [CrossRef]
- Geske, M.; Heuer, M.; Heideck, G.; Styczynski, Z. Current density distribution mapping in pem fuel cells as an instrument for operational measurements. Energies 2010, 3, 770–783. [Google Scholar] [CrossRef]
- Candusso, D.; Poirot-Crouvezier, J.P.; Bador, B.; Rullière, E.; Soulier, R.; Voyant, J.Y. Determination of current density distribution in proton exchange membrane fuel cells. Eur. Phys. J.-Appl. Phys. 2004, 25, 67–74. [Google Scholar] [CrossRef]
- Peng, L.; Shao, H.; Qiu, D.; Yi, P.; Lai, X. Investigation of the non-uniform distribution of current density in commercial-size proton exchange membrane fuel cells. J. Power Sources 2020, 453, 227836. [Google Scholar] [CrossRef]
- Nishikawa, H.; Kurihara, R.; Sukemori, S.; Sugawara, T.; Kobayasi, H.; Abe, S.; Aoki, T.; Ogami, Y.; Matsunaga, A. Measurements of humidity and current distribution in a pefc. J. Power Sources 2006, 155, 213–218. [Google Scholar] [CrossRef]
- Nasu, T.; Matsushita, Y.; Okano, J.; Okajima, K. Study of current distribution in pemfc stack using magnetic sensor probe. J. Int. Counc. Electr. Eng. 2012, 2, 391–396. [Google Scholar] [CrossRef]
- Akimoto, Y.; Okajima, K.; Uchiyama, Y. Evaluation of current distribution in a pemfc using a magnetic sensor probe. Energy Procedia 2015, 75, 2015–2020. [Google Scholar] [CrossRef][Green Version]
- Gerard, M.; Poirot-Crouvezier, J.-P.; Hissel, D.; Pera, M.-C. Oxygen starvation analysis during air feeding faults in pemfc. Int. J. Hydrog. Energy 2010, 35, 12295–12307. [Google Scholar] [CrossRef]
- Simulation Services. Available online: http://splusplus.com (accessed on 3 March 2022).
- Hauer, K.-H.; Potthast, R.; Wüster, T.; Stolten, D. Magnetotomography—A new method for analysing fuel cell performance and quality. J. Power Sources 2005, 143, 67–74. [Google Scholar] [CrossRef]
- Hamaz, T.; Cadet, C.; Druart, F.; Cauffet, G. Diagnosis of pem fuel cell stack based on magnetic fields measurements. IFAC Proc. Vol. 2014, 47, 11482–11487. [Google Scholar] [CrossRef]
- Le Ny, M.; Chadebec, O.; Cauffet, G.; Dedulle, J.-M.; Bultel, Y.; Rosini, S.; Fourneron, Y.; Kuo-Peng, P. Current distribution identification in fuel cell stacks from external magnetic field measurements. IEEE Trans. Magn. 2013, 49, 1925–1928. [Google Scholar] [CrossRef]
- Le Ny, M.; Chadebec, O.; Cauffet, G.; Rosini, S.; Bultel, Y. Pemfc stack diagnosis based on external magnetic field measurements. J. Appl. Electrochem. 2015, 45, 667–677. [Google Scholar] [CrossRef]
- Ifrek, L.; Chadebec, O.; Rosini, S.; Cauffet, G.; Bultel, Y.; Bannwarth, B. Fault identification on a fuel cell by 3-d current density reconstruction from external magnetic field measurements. IEEE Trans. Magn. 2019, 55, 1–5. [Google Scholar] [CrossRef]
- Ifrek, L.; Rosini, S.; Cauffet, G.; Chadebec, O.; Rouveyre, L.; Bultel, Y. Fault detection for polymer electrolyte membrane fuel cell stack by external magnetic field. Electrochim. Acta 2019, 313, 141–150. [Google Scholar] [CrossRef]
- Li, Z.; Cadet, C.; Outbib, R. Diagnosis for pemfc based on magnetic measurements and data-driven approach. IEEE Trans. Energy Convers. 2018, 34, 964–972. [Google Scholar] [CrossRef]
- Liu, Z.; Sun, Y.; Mao, L.; Zhang, H.; Jackson, L.; Wu, Q.; Lu, S. Efficient fault diagnosis of proton exchange membrane fuel cell using external magnetic field measurement. Energy Convers. Manag. 2022, 266, 115809. [Google Scholar] [CrossRef]
- LaManna, J.M.; Chakraborty, S.; Gagliardo, J.J.; Mench, M.M. Isolation of transport mechanisms in pefcs using high resolution neutron imaging. Int. J. Hydrog. Energy 2014, 39, 3387–3396. [Google Scholar] [CrossRef]
- Plait, A.; Giurgea, S.; Hissel, D.; Espanet, C. New magnetic field analyzer device dedicated for polymer electrolyte fuel cells noninvasive diagnostic. Int. J. Hydrog. Energy 2020, 45, 14071–14082. [Google Scholar] [CrossRef]
- Le Ny, M.; Chadebec, O.; Cauffet, G.; Dedulle, J.-M.; Bultel, Y. A three dimensional electrical model of pemfc stack. Fuel Cells 2012, 12, 225–238. [Google Scholar] [CrossRef]
- Larminie, J.; Dicks, A.; McDonald, M.S. Fuel Cell Systems Explained; J. Wiley: Chichester, UK, 2003; Volume 2. [Google Scholar]
- Görgün, H.; Arcak, M.; Barbir, F. An algorithm for estimation of membrane water content in pem fuel cells. J. Power Sources 2006, 157, 389–394. [Google Scholar] [CrossRef]
- Altair®, User Guide Flux® 12.3. 2020, Volume 3. Available online: http://www.altair.com/flux (accessed on 3 March 2022).
- Ifrek, L.; Cauffet, G.; Chadebec, O.; Bultel, Y.; Rosini, S.; Rouveyre, L. 2d and 3d fault basis for fuel cell diagnosis by external magnetic field measurements. Eur. Phys. J. Appl. Phys. 2017, 79, 20901. [Google Scholar] [CrossRef]
- Coey, J.M.D. Magnetism and Magnetic Materials; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Meunier, G.; Le Floch, Y.; Guérin, C. A nonlinear circuit coupled tt/sub 0/-/spl phi/formulation for solid conductors. IEEE Trans. Magn. 2003, 39, 1729–1732. [Google Scholar] [CrossRef]



| (V) | ||||
|---|---|---|---|---|
| 1.25 | 1.4 | 60 | 0.5 |
| Plates | Materials | Resistivity | Dimension (mm2) | Thickness (mm) | |
|---|---|---|---|---|---|
| End plate | Aluminium | 1 | 30 | ||
| Bipolar Plate | Graphite | 1 | 2 | ||
| Normal : | |||||
| GDL | Carbon cloth | 1 | 0.5 | ||
| Fault: Insulator Infinite | |||||
| Ferromagnetic | Ni-Fe Family | ___ | 741 | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bawab, A.; Giurgea, S.; Depernet, D.; Hissel, D. An Innovative PEMFC Magnetic Field Emulator to Validate the Ability of a Magnetic Field Analyzer to Detect 3D Faults. Hydrogen 2023, 4, 22-41. https://doi.org/10.3390/hydrogen4010003
Bawab A, Giurgea S, Depernet D, Hissel D. An Innovative PEMFC Magnetic Field Emulator to Validate the Ability of a Magnetic Field Analyzer to Detect 3D Faults. Hydrogen. 2023; 4(1):22-41. https://doi.org/10.3390/hydrogen4010003
Chicago/Turabian StyleBawab, Ali, Stefan Giurgea, Daniel Depernet, and Daniel Hissel. 2023. "An Innovative PEMFC Magnetic Field Emulator to Validate the Ability of a Magnetic Field Analyzer to Detect 3D Faults" Hydrogen 4, no. 1: 22-41. https://doi.org/10.3390/hydrogen4010003
APA StyleBawab, A., Giurgea, S., Depernet, D., & Hissel, D. (2023). An Innovative PEMFC Magnetic Field Emulator to Validate the Ability of a Magnetic Field Analyzer to Detect 3D Faults. Hydrogen, 4(1), 22-41. https://doi.org/10.3390/hydrogen4010003