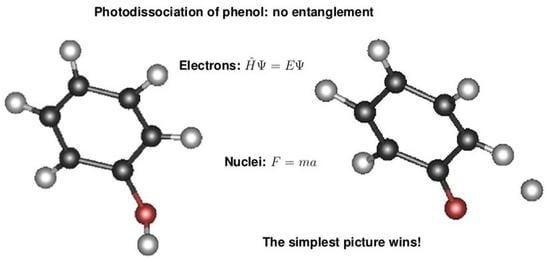
Classical Nuclear Motion: Comparison to Approaches with Quantum Mechanical Nuclear Motion
Abstract
1. Introduction
2. Methods
3. Results
3.1. Wave Packets and Alternatives
3.2. Multiple Spawning
3.3. Path Integrals
3.4. Full Treatment
4. Discussion
Supplementary Materials
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AIMD | Ab initio molecular dynamics |
| BOMD | Born–Oppenheimer molecular dynamics |
| CPMD | Car–Parrinello molecular dynamics |
| DFT | Density functional theory |
| ESIPT | Excited-state intramolecular proton transfer |
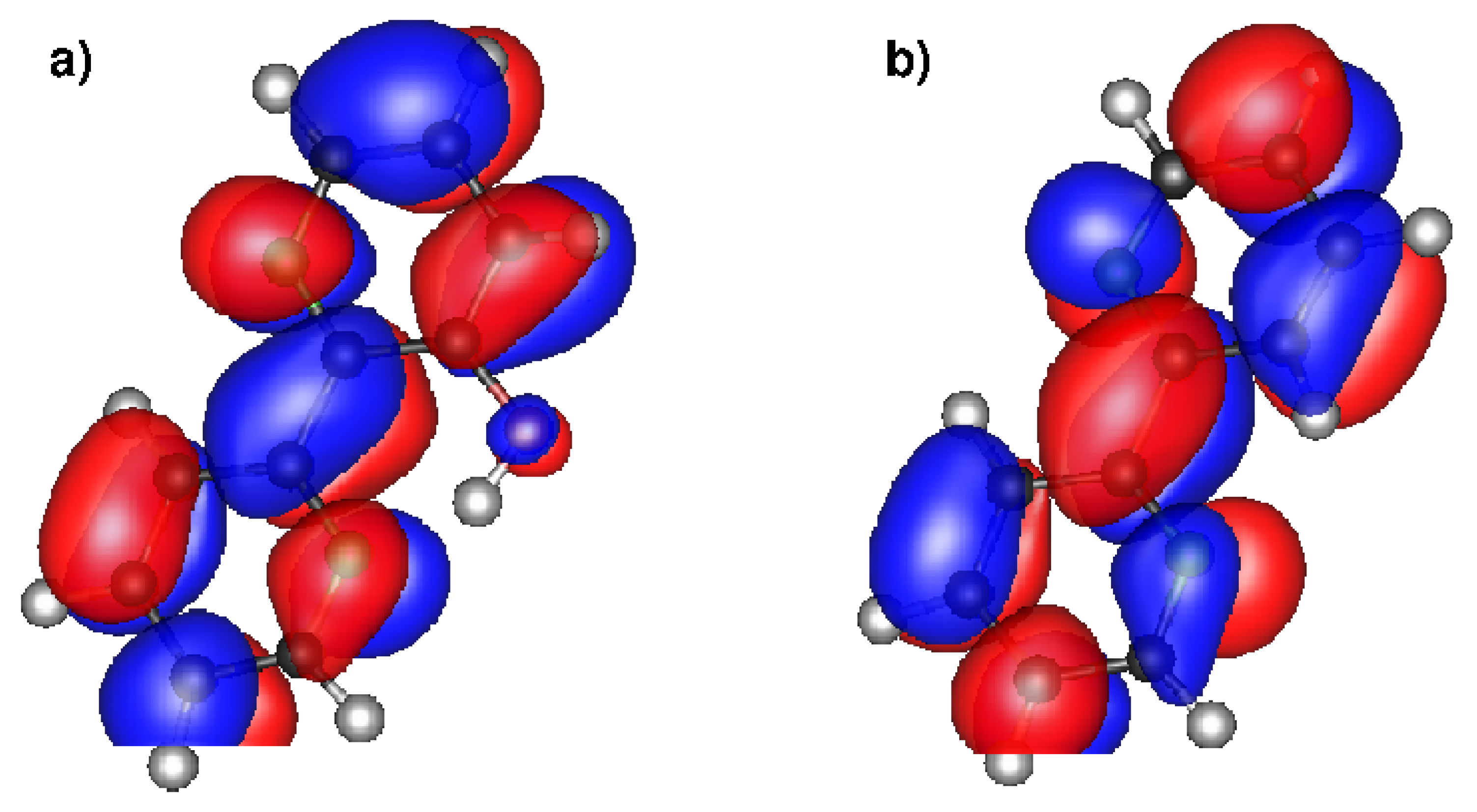
| HOMO | Highest occupied molecular orbital |
| LUMO | Lowest unoccupied molecular orbital |
| NEO | Nuclear-electronic orbital method |
| QM/MM | Quantum mechanics/molecular mechanics |
| ROKS | Restricted open-shell Kohn–Sham theory |
| SCF | Self-consistent field theory |
| TDDFT | Time-dependent DFT |
References
- Frank, I.; Genuit, S.; Matz, F.; Oschinski, H. Ammonia, water, and hydrogen: Can nuclear motion be described classically? Int. J. Quantum Chem. 2020, 120, e26142. [Google Scholar] [CrossRef]
- Frank, I. Classical motion of the nuclei in a molecules: A concept without alternatives. Chem. Sel. 2020, 5, 1872. [Google Scholar] [CrossRef]
- Büchel, R.C.; Rudolph, D.A.; Frank, I. Deterministic quantum mechanics: The role of the Maxwell-Boltzmann distribution. Int. J. Quantum Chem. 2021, 121, e26555. [Google Scholar] [CrossRef]
- Car, R.; Parrinello, M. Unified Approach for Molecular Dynamics and Density-Functional Theory. Phys. Rev. Lett. 1985, 55, 2471–2474. [Google Scholar] [CrossRef] [PubMed]
- Hutter, J.; Hutter, J.; Alavi, A.; Deutsch, T.; Bernasconi, M.; Goedecker, S.; Marx, D.; Tuckerman, M.; Parrinello, M. Version 4.3, Copyright IBM Corp 1990–2015, Copyright MPI für Festkörperforschung Stuttgart 1997–2001. Available online: http://www.cpmd.org/ (accessed on 22 October 2022).
- Marx, D.; Parrinello, M. Ab initio path-integral molecular dynamics. Z. Phys. B 1994, 95, 143. [Google Scholar] [CrossRef]
- Marx, D.; Parrinello, M. Structural quantum effects and three-centre two-electron bonding in CH5+. Nature 1995, 375, 216. [Google Scholar] [CrossRef]
- Marx, D.; Parrinello, M. Ab initio path-integral molecular dynamics: Basic ideas. J. Chem. Phys. 1996, 104, 4077. [Google Scholar] [CrossRef]
- Marx, D.; Parrinello, M. The effect of quantum and thermal fluctuations on the structure of the floppy molecule C2H3+. Science 1996, 271, 179. [Google Scholar] [CrossRef]
- Lan, Z.; Domcke, W.; Vallet, V.; Sobolewski, A.L.; Mahapatra, S. Time-dependent quantum wave-packet description of the 1πσ* photochemistry of phenol. J. Chem. Phys. 2005, 122, 224315. [Google Scholar] [CrossRef]
- Domcke, W.; Yarkony, D.R. Role of Conical Intersections in Molecular Spectroscopy and Photoinduced Chemical Dynamics. Annu. Rev. Phys. Chem. 2012, 63, 325. [Google Scholar] [CrossRef]
- Ramesh, S.G.; Domcke, W. A multi-sheeted three-dimensional potential-energy surface for the H-atom photodissociation of phenol. Faraday Discuss. 2013, 163, 73. [Google Scholar] [CrossRef]
- Xie, W.; Domcke, W. Accuracy of trajectory surface-hopping methods: Test for a two-dimensional model of the photodissociation of phenol. J. Chem. Phys. 2017, 147, 184114. [Google Scholar] [CrossRef]
- Webb, S.P.; Iordanov, T.; Hammes-Schiffer, S. Multiconfigurational nuclear-electronic orbital approach: Incorporation of nuclear quantum effects in electronic structure calculations. J. Chem. Phys. 2002, 117, 4106. [Google Scholar] [CrossRef]
- Ben-Nun, M.; Quenneville, J.; Martinez, T. Ab Initio Multiple Spawning: Photochemistry from First Principles Quantum Molecular Dynamics. J. Phys. Chem. A 2000, 104, 5161. [Google Scholar] [CrossRef]
- Curchod, B.F.E.; Martinez, T.J. Ab Initio Nonadiabatic Quantum Molecular Dynamics. Chem. Rev. 2018, 118, 3305. [Google Scholar] [CrossRef]
- Frank, I.; Hutter, J.; Marx, D.; Parrinello, M. Molecular dynamics in low-spin excited states. J. Chem. Phys. 1998, 108, 4060. [Google Scholar] [CrossRef]
- Tavernelli, I.; Röhrig, U.; Roethlisberger, U. Molecular dynamics in electronically excited states using time-dependent density functional theory. Mol. Phys. 2005, 103, 963. [Google Scholar] [CrossRef]
- Alonso, J.L.; Andrade, X.; Echenique, P.; Falceto, F.; Prada-Gracia, D.; Rubio, A. Efficient Formalism for Large-Scale Ab Initio Molecular Dynamics based on Time-Dependent Density Functional Theory. Phys. Rev. Lett. 2008, 101, 096403. [Google Scholar] [CrossRef]
- Lopata, K.; Govind, N. Modelling Fast Electron Dynamics with Real-Time Time-Dependent Density Functional Theory: Application to Small Molecules and Chromophores. J. Chem. Theory Comput. 2011, 7, 1344. [Google Scholar] [CrossRef]
- Lian, C.; Hu, S.Q.; Guan, M.X.; Meng, S. Momentum-resolved TDDFT algorithm in atomic basis for real time tracking of electronic excitation. J. Chem. Phys. 2018, 149, 154104. [Google Scholar] [CrossRef]
- Lian, C.; Ali, Z.A.; Kwon, H.; Wong, B.M. Indirect but Efficient: Laser-Excited Electrons Can Drive Ultrafast Polarization Switching in Ferroelectroc Materials. J. Phys. Chem. Lett. 2019, 10, 3402. [Google Scholar] [CrossRef] [PubMed]
- Marx, D.; Hutter, J. Ab Initio Molecular Dynamics: Basic Theory and Advanced Methods; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef] [PubMed]
- Troullier, N.; Martins, J.L. Efficient Pseudopotentials for Plane-Wave Calculations. Phys. Rev. B 1991, 43, 1993. [Google Scholar] [CrossRef] [PubMed]
- Boero, M.; Parrinello, M.; Terakura, K.; Weiss, H. Car-Parrinello study of Ziegler-Natta heterogeneous catalysis: Stability and destabilization problems of the active site models. Mol. Phys. 2002, 100, 2935–2940. [Google Scholar] [CrossRef]
- Bernardi, F.; Olivucci, M.; Robb, M.A. Potential energy surface crossings in organic photochemistry. Chem. Soc. Rev. 1996, 25, 321. [Google Scholar] [CrossRef]
- Nonnenberg, C.; Grimm, S.; Frank, I. Restricted open-shell Kohn-Sham theory for π-π* transitions. II. Simulation of photochemical reactions. J. Chem. Phys. 2003, 119, 11585. [Google Scholar] [CrossRef]
- Frank, I.; Damianos, K. Restricted Open-Shell Kohn-Sham Theory: Simulation of the Pyrrole Photodissociation. J. Chem. Phys. 2007, 126, 125105. [Google Scholar] [CrossRef]
- Shu, Y.; Truhlar, D.G. Diabatization by machine intelligence. J. Chem. Theory Comput. 2020, 16, 6456. [Google Scholar] [CrossRef]
- Sobolewski, A.L.; Domcke, W. Photoinduced Electron and Proton Transfer in Phenol and Its Clusters with Water and Ammonia. J. Phys. Chem. A 2001, 105, 9275. [Google Scholar] [CrossRef]
- Ben-Nun, M.; Molnar, F.; Lu, H.; Phillips, J.C.; Martinez, T.J.; Schulten, K. Quantum dynamics of the femtosecond photoisomerization of retinal in bacteriorhodopsin. Faraday Discuss. 1998, 110, 447. [Google Scholar] [CrossRef]
- Röhrig, U.; Guidoni, L.; Laio, A.; Frank, I.; Röthlisberger, U. A molecular spring for vision. J. Am. Chem. Soc. 2004, 126, 15328. [Google Scholar] [CrossRef]
- Feynman, R.P.; Leighton, R.B.; Sands, M. The Feynman Lectures on Physics, 2nd ed.; Pearson Education: London, UK; California Institute of Technology: Pasadena, CA, USA, 2006. [Google Scholar]
- Yu, Q.; Pavosevic, F.; Hammes-Schiffer, S. Development of nuclear basis sets for multicomponent quantum chemistry methods. J. Chem. Phys. 2020, 152, 244123. [Google Scholar] [CrossRef]
- Tao, Z.; Roy, S.; Schneider, P.E.; Pavosevic, F.; Hammes-Schiffer, S. Analytical Gradients for Nuclear–Electronic Orbital Time-Dependent Density Functional Theory: Excited-State Geometry Optimizations and Adiabatic Excitation Energies. J. Chem. Theory Comput. 2021, 17, 5110. [Google Scholar] [CrossRef]
- Rohloff, E.; Rudolph, D.A.; Strolka, O. Classical nuclear motion: Does it fail to explain reactions and spectra in certain cases? Int. J. Quantum Chem. 2022, 122, e26902. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frank, I. Classical Nuclear Motion: Comparison to Approaches with Quantum Mechanical Nuclear Motion. Hydrogen 2023, 4, 11-21. https://doi.org/10.3390/hydrogen4010002
Frank I. Classical Nuclear Motion: Comparison to Approaches with Quantum Mechanical Nuclear Motion. Hydrogen. 2023; 4(1):11-21. https://doi.org/10.3390/hydrogen4010002
Chicago/Turabian StyleFrank, Irmgard. 2023. "Classical Nuclear Motion: Comparison to Approaches with Quantum Mechanical Nuclear Motion" Hydrogen 4, no. 1: 11-21. https://doi.org/10.3390/hydrogen4010002
APA StyleFrank, I. (2023). Classical Nuclear Motion: Comparison to Approaches with Quantum Mechanical Nuclear Motion. Hydrogen, 4(1), 11-21. https://doi.org/10.3390/hydrogen4010002