Laser Trapping Technique for Measuring Ionization Energy and Identifying Hemoglobin Through Charge Quantification in Blood Samples
Abstract
1. Introduction
2. Experimental Method: Hemoglobin Analysis and Single-Cell Manipulation
2.1. Hemoglobin Quantitation and Sample Preparation
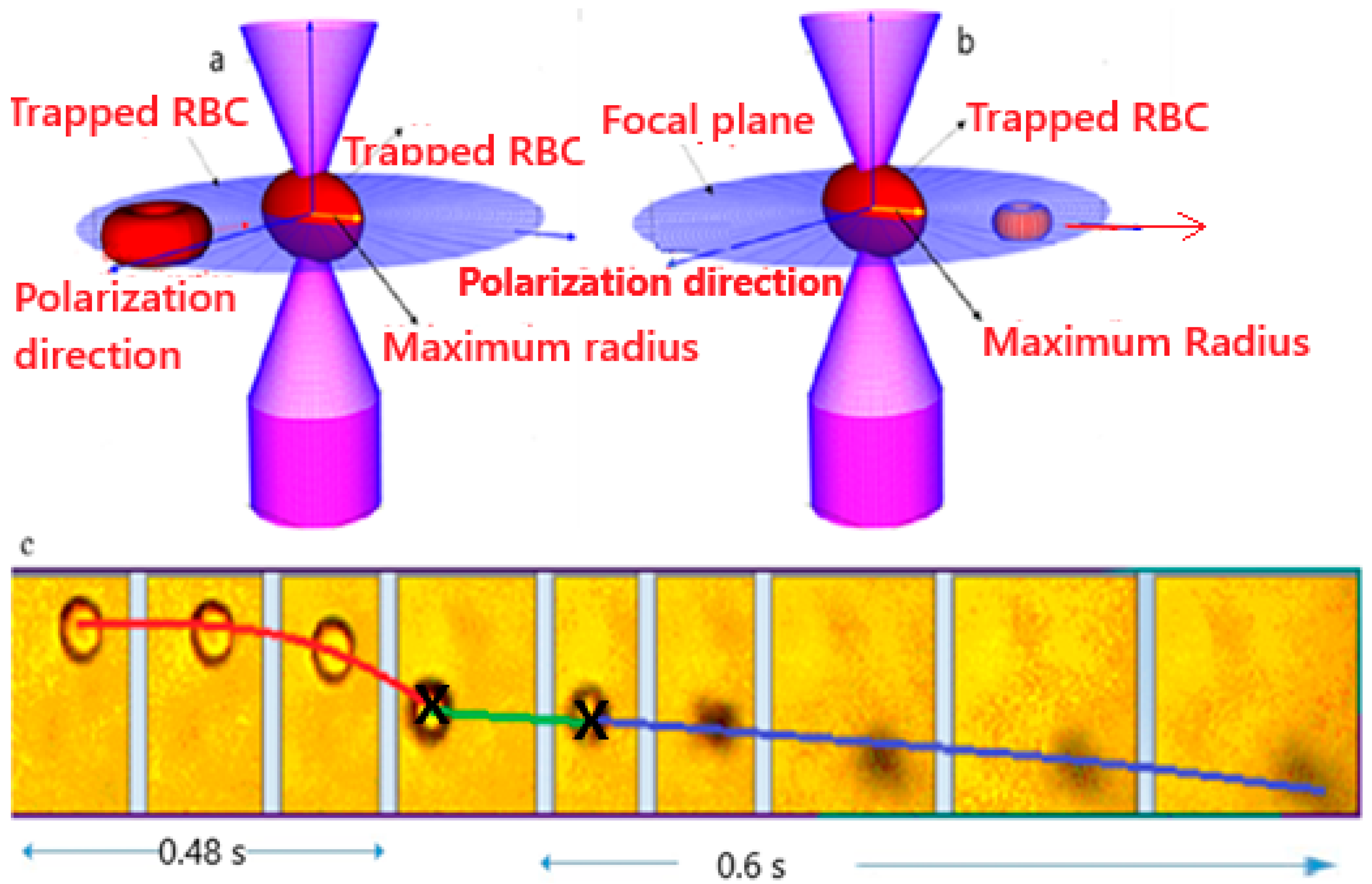
2.2. Laser Trapping and Single Cell Ionization
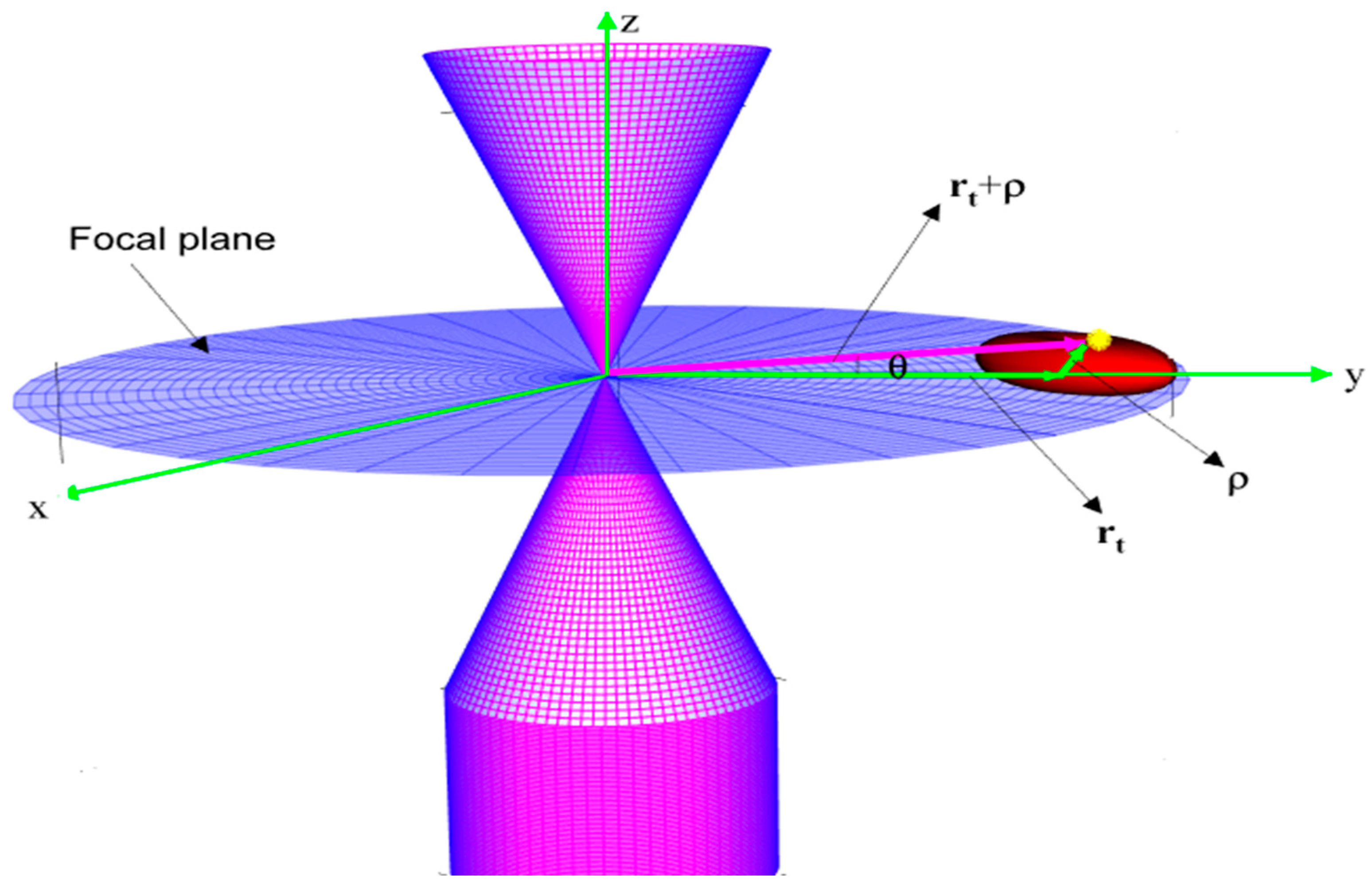
2.3. Theoretical Model
2.3.1. The Electrical Force
2.3.2. The Drag Force
2.3.3. Radiation Pressure Force
2.3.4. Gravitational and Buoyancy Force
2.3.5. The Trapping Force
2.3.6. General Equation of Motion as the Trap Is Ejected from the Trap
- is the drag coefficient;
- is the trap stiffness;
- is the cell charge;
- is the amplitude of the electric field;
- is the cell mass.
2.3.7. Cell Volume and Mass
2.3.8. Energy and Dose Metrics (TIE* and TRD*)
2.4. Image Analysis and Tracking
2.5. Parameter Estimation Procedure
- Construct using the boxed equation above.
- Choose the fitting domain. Use data from (post-ionization ejection).
- Model choice. Fit either the velocity form
- 4.
- Parameters. with constraints , .
- 5.
- Estimation. Nonlinear least squares (Levenberg–Marquardt) minimizing (or the analogous sum for velocities).
- 6.
- Pooling strategy. Because optical geometry is shared within an experiment, is estimated globally across cells from the same run, while and vary per cell to capture near-wall and morphological variability.
- 7.
- Uncertainty. Report fit SEs and mean ± SD across cells. Goodness of fit (RMSE and ) is summarized in the Section 3.
- 8.
- Derived quantities. Using the same , compute TIE* (integral up to ) and TRD* () for each cell; then report the group means ± SD by variant.
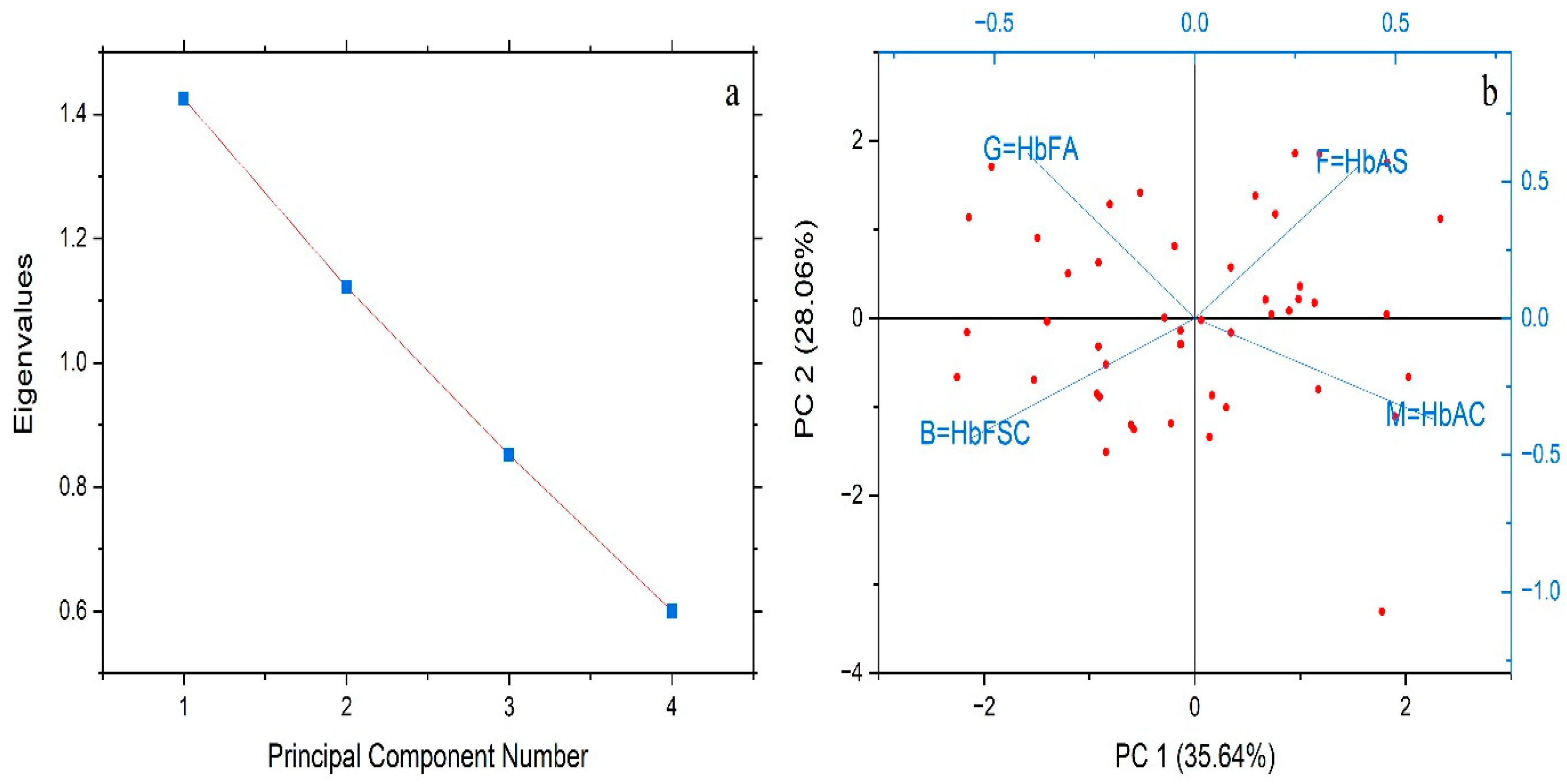
3. Results
3.1. Data Analysis
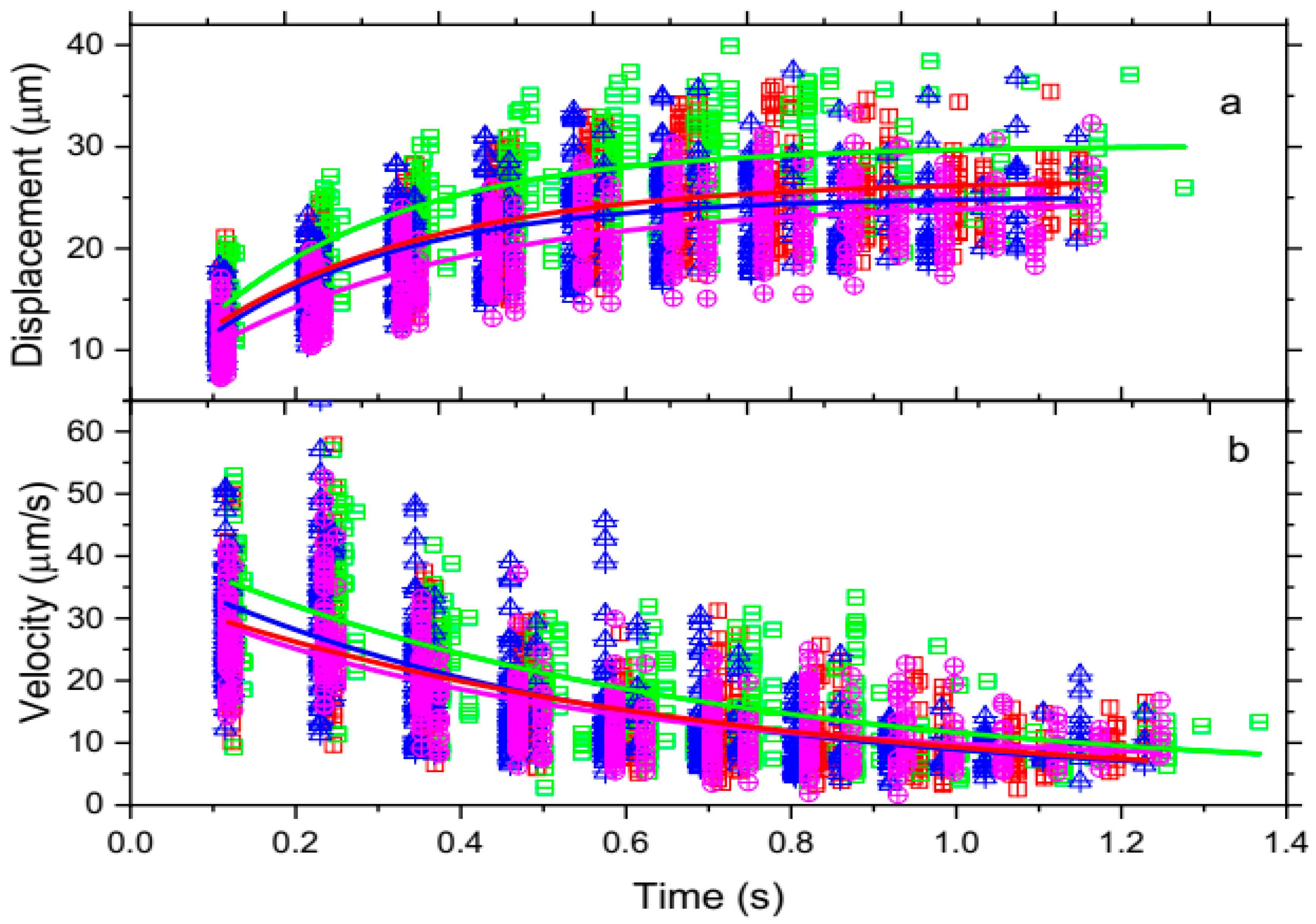
3.1.1. Trajectories of Optically Trapped RBC Motion from Four Blood Samples as a Function of Time
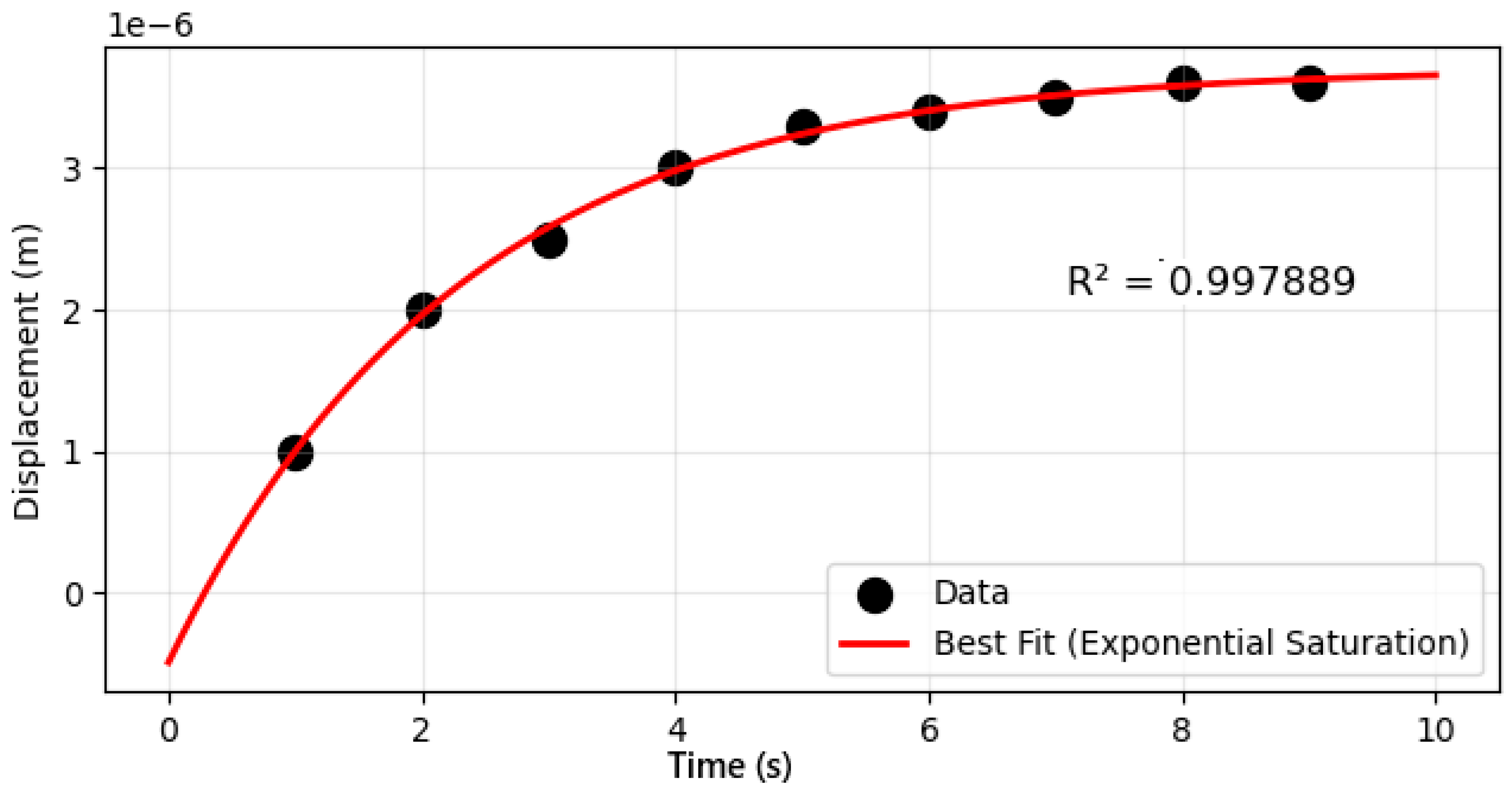
3.1.2. Laser-Induced Ionization Dynamics of Single Red Blood Cells
3.1.3. Charge Profiles of Single Hemoglobin Variants
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sharma, S.; Hashmi, M.; Chakraborty, R. StatPearls [Internet]; StatPearls Publishing: Treasure Island, FL, USA, 2021. [Google Scholar]
- Kato, G.J.; Piel, F.B.; Reid, C.D.; Gaston, M.H.; Ohene-Frempong, K.; Krishnamurti, L.; Smith, W.R.; Panepinto, J.A.; Weatherall, D.J.; Costa, F.F.; et al. Sickle Cell Disease. Nat. Rev. Dis. Primers 2018, 4, 18010. [Google Scholar] [CrossRef]
- Needs, T.; Gonzalez-Mosquera, L.F.; Lynch, D.T. Beta Thalassemia. In StatPearls; StatPearls Publishing: Treasure Island, FL, USA, 2018. [Google Scholar]
- Bachir, D.; Ga Bachir, D.; Galactéros, F. The Management of Sickle Cell Disease. Orphanet J. Rare Dis. 2004, 1, 1–7. [Google Scholar] [CrossRef]
- Cohn, E.J.; Edsall, J.T. Proteins, Amino Acids and Peptides as Ions and Dipolar Ions; Reprinted in Ergebn. Physiol 1947, 43, 1–89; Reinhold Publishing Corporation: New York, NY, USA, 1943. [Google Scholar] [CrossRef]
- Havinga, E. Comparison of the Phosphorus Content, Optical Rotation, Separation of Hemes and Globin, and Terminal Amino Acid Residues of Normal Adult Human Hemoglobin and Sickle Cell Anemia Hemoglobin. Proc. Natl. Acad. Sci. USA 1953, 39, 59–64. [Google Scholar] [CrossRef] [PubMed]
- Scheinberg, I.H.; Harris, R.S.; Spitzer, J.L. Differential Titration by Means of Paper Electrophoresis and the Structure of Human Hemoglobins. Proc. Natl. Acad. Sci. USA 1954, 40, 777–783. [Google Scholar] [CrossRef] [PubMed]
- Kutlar, A.; Kutlar, F.; Wilson, J.B.; Headlee, M.G.; Huisman, T.H.J. Quantitation of Hemoglobin Components by High-Performance Cation-Exchange Liquid Chromatography: Its Use in Diagnosis and in the Assessment of Cellular Distribution of Normal and Abnormal Hemoglobin Variants. Am. J. Hematol. 1984, 17, 39–53. [Google Scholar] [CrossRef]
- Cooper, J.; Devito, D.; Solomon, R.; Brown, C.; Crogman, H.; Farone, A.; Farone, M.; Erenso, D.; Aguinaga, M.D.P. Laser Trapping for Single Red Blood Cell (RBC) Ionization and Measurement of Charge. In Biomedical Optics; BT3A.34; Optica Publishing Group: Washington, DC, USA, 2014. [Google Scholar]
- Ashkin, A. Applications of Laser Radiation Pressure. Science 1980, 210, 1081–1088. [Google Scholar] [CrossRef]
- Easterling, L.F.; Yerabolu, R.; Kumar, R.; Alzarieni, K.Z.; Kenttämaa, H.I. Factors Affecting the Limit of Detection for HPLC/Tandem Mass Spectrometry Experiments Based on Gas-Phase Ion–Molecule Reactions. Anal. Chem. 2020, 92, 7471–7477. [Google Scholar] [CrossRef]
- Snyder, L.R.; Kirkland, J.J.; Dolan, J.W. Introduction to Modern Liquid Chromatography, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2010; ISBN 978-0-470-16054-0. [Google Scholar]
- Khera, R.; Singh, T.; Khurana, N.; Gupta, N.; Dubey, A. HPLC in Characterization of Hemoglobin Profile in Thalassemia Syndromes and Hemoglobinopathies: A Clinicohematological Correlation. Indian J. Hematol. Blood Transfus. 2015, 31, 110–115. [Google Scholar] [CrossRef]
- Ali, A.H. High-Performance Liquid Chromatography (HPLC): A Review. Ann. Adv. Chem. 2022, 6, 10–20. [Google Scholar] [CrossRef]
- Pellizzaro, A.; Welker, G.; Scott, D.; Solomon, R.; Cooper, J.; Farone, A.; Farone, M.; Mushi, R.S.; del Pilar Aguinaga, M.; Erenso, D. Direct Laser Trapping for Measuring the Behavior of Transfused Erythrocytes in a Sickle Cell Anemia Patient. Biomed. Opt. Express 2012, 3, 2190–2199. [Google Scholar] [CrossRef]
- Dolan, J. How Much Retention Time Variation Is Normal? LC Resources: Lafayette, CA, USA, 2014; Available online: https://www.chromatographyonline.com (accessed on 13 September 2025).
- Sammartano, A.; Migliari, S.; Serreli, G.; Scarlattei, M.; Baldari, G.; Ruffini, L. Validation of the HPLC Analytical Method for the Determination of Chemical and Radiochemical Purity of Ga-68-DOTATATE. Indian J. Nucl. Med. 2023, 38, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Alquadeib, B.T. Development and Validation of a New HPLC Analytical Method for the Determination of Diclofenac in Tablets. Saudi Pharm. J. 2019, 27, 66–70. [Google Scholar] [CrossRef]
- Kelley, M.; Cooper, J.; Devito, D.; Mushi, R.; Aguinaga, M.D.P.; Erenso, D.B. Laser Trap Ionization for Identification of Human Erythrocytes with Variable Hemoglobin Quantitation. J. Biomed. Opt. 2018, 23, 055005. [Google Scholar] [CrossRef]
- Muhammed, E.; Cooper, J.; Devito, D.; Mushi, R.; del Pilar Aguinaga, M.; Erenso, D.; Crogman, H. Elastic Property of Sickle Cell Anemia and Sickle Cell Trait Red Blood Cells. J. Biomed. Opt. 2021, 26, 096502. [Google Scholar] [CrossRef]
- Muhammed, E.; Chen, L.; Gao, Y.; Erenso, D. Chemo-Treated 4T1 Breast Cancer Cells Radiation Response Measured by Single and Multiple Cell Ionization Using Infrared Laser Trap. Sci. Rep. 2019, 9, 17547. [Google Scholar] [CrossRef] [PubMed]
- Goangul, M.S.; Erenso, D.B.; Gao, Y.; Chen, L.; Eshun, K.O.; Alvarez, G.; Crogman, H.T. Assessing Radiation Effects on Chemo-Treated BT20 and 4T1 Breast Cancer, and Neuroblastoma Cell Lines: A Study of Single and Multiple-Cell Ionization via Infrared Laser Trapping. Radiat 2024, 4, 85–100. [Google Scholar] [CrossRef]
- Goangul, M.S.; Stewart, W.C.; Erenso, D.; Crogman, H.T. The Radiation Response Measurement of a Single and Multiple Cell Ionization of Neuroblastoma Cells by Infrared Laser Trap. J. Radiat. Res. 2023, 64, 113–125. [Google Scholar] [CrossRef]
- Kelley, M.; Gao, Y.; Erenso, D. Single Cell Ionization by a Laser Trap: A Preliminary Study in Measuring Radiation Dose and Charge in BT20 Breast Carcinoma Cells. Biomed. Opt. Express 2016, 7, 3438–3448. [Google Scholar] [CrossRef]
- Bogdanova, A.; Kaestner, L.; Simionato, G.; Wickrema, A.; Makhro, A. Heterogeneity of Red Blood Cells: Causes and Consequences. Front. Physiol. 2020, 11, 392. [Google Scholar] [CrossRef]
- Gurkan, U.A. Biophysical and Rheological Biomarkers of Red Blood Cell Physiology and Pathophysiology. Curr. Opin. Hematol. 2021, 28, 138–149. [Google Scholar] [CrossRef]
- Igbineweka, N.E.; van Loon, J.J.W.A. Gene-Environmental Influence of Space and Microgravity on Red Blood Cells with Sickle Cell Disease. NPJ Genom. Med. 2024, 9, 44. [Google Scholar] [CrossRef]
- Muhammed, E.; Erenso, D.B.; Gao, Y.; Chen, L.; Kelley, M.; Vazquez, C.; Gale, M.; Nichols, C.; Crogman, H.T. Measurement of Charge and Refractive Indices in Optically Trapped and Ionized Living Cells. Tomography 2022, 8, 70–88. [Google Scholar] [CrossRef] [PubMed]
- Ishikawa, T.; Kawabata, N.; Imai, Y.; Tsubota, K.-I.; Yamaguchi, T. Numerical Simulation of a Low-Hematocrit Blood Flow in a Small Artery with Stenosis. J. Biomech. Sci. Eng. 2007, 2, 12–22. [Google Scholar] [CrossRef]
- Udroiu, I. Estimation of Erythrocyte Surface Area in Mammals. arXiv 2014, arXiv:1403.7660. [Google Scholar] [CrossRef]
- Norouzi, N.; Bhakta, H.C.; Grover, W.H. Sorting Cells by Their Density. PLoS ONE 2017, 12, e0180520. [Google Scholar] [CrossRef]
- Piskin, E.; Cianciosi, D.; Gulec, S.; Tomas, M.; Capanoglu, E. Iron Absorption: Factors, Limitations, and Improvement Methods. ACS Omega 2022, 7, 20441–20456. [Google Scholar] [CrossRef]
- Kang, Y.; Douglas, D. Gas-Phase Ions of Human Hemoglobin A, F, and S. J. Am. Soc. Mass Spectrom. 2011, 22, 1187–1196. [Google Scholar] [CrossRef] [PubMed]
- Gerritsma, J.; Sinnige, D.; Drieze, C.; Sittrop, B.; Houtsma, P.; Ulshorst-Jansen, N.H.; Huisman, W. Quantitative and Qualitative Analysis of Haemoglobin Variants Using Capillary Zone Electrophoresis. Ann. Clin. Biochem. 2000, 37, 380–389. [Google Scholar] [CrossRef] [PubMed]
- Papadea, C.; Cate, J.C., 4th. Identification and Quantification of Hemoglobins A, F, S, and C by Automated Chromatography. Clin. Chem. 1996, 42, 57–63. [Google Scholar] [CrossRef]
- Sridhar, A.; Idowu, M. Hemoglobin Electrophoresis in Sickle Cell Disease: A Primer for the Clinician. Lab. Med. 2021, 52, 321–326. [Google Scholar]
- Ghosh, K.; Ghosh, K.; Agrawal, R.; Nadkarni, A.H. Recent Advances in Screening and Diagnosis of Hemoglobinopathy. Expert. Rev. Hematol. 2020, 13, 13–21. [Google Scholar] [CrossRef] [PubMed]





| Hb Fractions Profile | Hb AS | Hb AC | Hb FSC | Hb FA |
|---|---|---|---|---|
| Sex | M | F | M | F |
| Age | 38 years | 30 years | 75 days | 82 days |
| Hb fractions profile relative percentage of hemoglobin types by HPLC | ||||
| Hb A (%) | 53.20 | 55.41 | 0.00 | 29.10 |
| Hb A2 (%) | 3.60 | 3.10 | 0.20 | 0.80 |
| Hb C (%) | 0.00 | 41.09 | 7.10 | 0.00 |
| Hb F (%) | 0.40 | 0.40 | 82.60 | 70.10 |
| Hb S (%) | 42.80 | 0.00 | 7.10 | 0.00 |
| Blood Sample | Measurement Parameter | Mean | SD | Minimum | Maximum |
|---|---|---|---|---|---|
| Hb AS | TRD* (J/ng) | 0.75 | 0.38 | 0.03 | 1.63 |
| TIE* (mJ) | 178.00 | 91.98 | 8.71 | 358.86 | |
| Radius (µm) | 8.73 | 0.64 | 6.50 | 10.33 | |
| Trap stiffness k (N/m) | 4.89 × 10−3 | 4.14 × 10−4 | 4.04 × 10−3 | 6.76 × 10−3 | |
| Z-number | 2943.32 | 991.96 | 1363.30 | 5432.73 | |
| Z-number/volume | 13.79 | 4.64 | 6.37 | 27.10 | |
| Hb AC | TRD* (J/ng) | 0.89 | 0.55 | 0.27 | 2.67 |
| TIE* (mJ) | 183.78 | 103.86 | 85.63 | 534.79 | |
| Radius (µm) | 8.35 | 1.13 | 6.55 | 11.11 | |
| Trap stiffness k (N/m) | 5.00 × 10−3 | 6.74 × 10−4 | 3.86 × 10−3 | 6.23 × 10−3 | |
| Z-number | 3333.47 | 839.73 | 1656.66 | 5943.2 | |
| Z-number/volume | 37.87 | 9.12 | 24.80 | 72.63 | |
| Hb FA | TRD* (J/ng) | 1.42 | 1.95 | 1.12 | 1.64 |
| TIE* (mJ) | 201.90 | 97.42 | 102.93 | 205.86 | |
| Radius (µm) | 6.90 | 0.75 | 5.22 | 9.10 | |
| Trap stiffness k (N/m) | 9.49 × 10−3 | 3.13 × 10−3 | 4.05 × 10−3 | 1.80 × 10−2 | |
| Z-number | 2428.87 | 814.38 | 2223.61 | 2634.13 | |
| Z-number/volume | 18.78 | 6.42 | 6.46 | 36.51 | |
| Hb FSC | TRD* (J/ng) | 1.31 | 0.65 | 0.37 | 3.32 |
| TIE* (mJ) | 190.01 | 94.21 | 85.22 | 596.56 | |
| Radius (µm) | 6.91 | 0.88 | 5.24 | 9.28 | |
| Trap stiffness k (N/m) | 9.74 × 10−3 | 4.09 × 10−3 | 3.22 × 10−3 | 2.40 × 10−2 | |
| Z-number | 3006.58 | 704.58 | 1337.81 | 5633.66 | |
| Z-number/volume | 23.34 | 8.3301 | 8.80 | 39.41 |
| Blood Types | Hb AS | Hb AC | Hb FSC | Hb FA | |
|---|---|---|---|---|---|
| Hb S | Z-number | 1264.00 | 0 | 346 | 0 |
| Percent, % | 42.94% | 0 | 11.51% | 0 | |
| Hb C | Z-number | 0 | 1420.11 | 346 | 0 |
| Percent, | 0 | 45.82% | 11.51% | 0 | |
| Hb A | Z-number | 1679.32 | 1679.32 | 0 | 492.1 |
| Percent, | 57.04% | 54.17% | 0 | 20% | |
| Hb F | Z-number | 0 | 0 | 2314.6 | 1828 |
| Percent, | 0 | 0 | 76.98 | 74.42 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Endris, E.M.; Adem, D.A.; Crogman, H.T.; Erenso, D.B. Laser Trapping Technique for Measuring Ionization Energy and Identifying Hemoglobin Through Charge Quantification in Blood Samples. Biophysica 2025, 5, 56. https://doi.org/10.3390/biophysica5040056
Endris EM, Adem DA, Crogman HT, Erenso DB. Laser Trapping Technique for Measuring Ionization Energy and Identifying Hemoglobin Through Charge Quantification in Blood Samples. Biophysica. 2025; 5(4):56. https://doi.org/10.3390/biophysica5040056
Chicago/Turabian StyleEndris, Endris M., Deresse A. Adem, Horace T. Crogman, and Daniel B. Erenso. 2025. "Laser Trapping Technique for Measuring Ionization Energy and Identifying Hemoglobin Through Charge Quantification in Blood Samples" Biophysica 5, no. 4: 56. https://doi.org/10.3390/biophysica5040056
APA StyleEndris, E. M., Adem, D. A., Crogman, H. T., & Erenso, D. B. (2025). Laser Trapping Technique for Measuring Ionization Energy and Identifying Hemoglobin Through Charge Quantification in Blood Samples. Biophysica, 5(4), 56. https://doi.org/10.3390/biophysica5040056






